Matematyka Dyskretna
Andrzej Szepietowski
Rozdział 1
Podstawowe poj˛ecia, oznaczenia
1.1
Sumy
Maj¸ac dany sko ´nczony ci¸aga1,a2,...ak, sum¸e jego elementów zapisujemy jako k
X
i=1
ai.
Niezbyt formalnie mo˙zemy to zapisa´c
k
X
i=1
ai = a1+ a2+ · · · + ak.
Jako przykład zastosujmy symbol sumy do zapisu wzoru na sum˛e ci¸agu arytmetycznego).
k
X
i=1
i = 1 + 2 + · · · + k = (k + 1)k
2 (1.1)
oraz wzoru na sum˛e ci¸agu geometrycznego).
k X i=0 xi= 1 + x + x2+ · · · + xk =x k+1− 1 x − 1 , (1.2)
(wzór (1.2) jest słuszny dla ka˙zdegox 6= 1)
B¸edziemy te˙z u˙zywa´c zapisu typu
X
1≤i≤6
ai= a1+ a2+ a3+ a4+ a5+ a6.
W tym przypadku zbiór indeksów okre´slony jest za pomoc¸a warunku pod znakiem sumy. Warunek okre´slaj¸acy indeksy, po których nale˙zy sumowa´c mo˙ze by´c bardziej skompliko-wany, na przykład X 1≤i≤6 i parzyste ai= a2+ a4+ a6. 3
Stosowa´c b¸edziemy tak˙ze zapis
X
i∈I
ai
oznaczaj¸acy sum¸e tych elementówai, których indeksy nale˙z¸a do sko ´nczonego zbioru
indeksówI. Na przykład, je˙zeli I = {1, 3, 5, 7}, to X
i∈I
ai = a1+ a3+ a5+ a7.
Mo˙zemy te˙z sumowa´c ci ˛agi, których elementy zale˙z ˛a od dwóch indeksów,
X
1≤i≤3 2≤j≤3
aij = a12+ a13+ a22+ a23+ a32+ a33.
Za pomoc ˛a podwójnej sumy mo˙zemy na przykład przedstawi ´c uogólnione prawo roz-dzielno´sci mno˙zenia wzgl˛edem dodawania:
X 1≤i≤m ai · X 1≤j≤n bj = X 1≤i≤m 1≤j≤n aibj (1.3)
a tak˙ze wzór na podnoszenie sumy do kwadratu:
X 1≤i≤m ai 2 = X 1≤i≤m a2i + X 1≤i<j≤m 2aiaj (1.4)
1.2
Iloczyny
Aby zapisa´c iloczyn elementów ci¸agua1,a2,...,ak, stosujemy zapis k
Y
i=1
ai.
Znów niezbyt formalnie mo˙zemy to zapisa´c jako
k
Y
i=1
ai= a1· a2· · · ak.
1.3
Wielomiany
Wielomian jest to funkcja postaci
1.3. Wielomiany 5
gdziex jest zmienn ˛a rzeczywist ˛a, aa0,a1, ... ,ans ˛a stałymi rzeczywistymi, nazywanymi
współczynnikami wielomianu. Stopniem wielomianuP (x) jest najwi˛eksze takie k, ˙ze ak6= 0, stopie´n oznaczamy, przez st(W (x)). Zwykle pisz ˛acP (x) = an· xn+ · · · + a0
b˛edziemy zakłada´c, ˙zean 6= 0, czyli ˙ze stopie´n st(P (x)) = n. U˙zywaj ˛ac symbolu sumy
wielomian mo˙zemy przedstawi´c w nast˛epuj ˛acy sposób:
P (x) =
n
X
i=0
aixi.
Wielomian, którego wszystkie współczynniki s ˛a równe zeru nazywamy wielomianem ze-rowym. Dwa wielomianyP (x) = Pn
i=0aixi orazQ(x) = Pni=0bixi s ˛a równe je˙zeli
maj ˛a takie same wspólczynniki, to znaczy je˙zeliai= bidla ka˙zdegoi.
Wielomiany mo˙zna dodawa´c, odejmowa´c lub mno˙zy´c. Suma, ró˙znica i iloczyn wie-lomianówP (x) i Q(x) okre´slone s ˛a nast˛epuj ˛aco:
• P (x) + Q(x) =Pn
i=0(ai+ bi)xi,
• P (x) − Q(x) =Pn
i=0(ai− bi)xi,
• P (x) · Q(x) =P2n
i=0(ci)xi, gdzieci=Pik=0ak· bi−k oraz ak = 0 i bk = 0
dla wszystkich k > n.
Wzór na iloczyn wielomianów wygl ˛ada skomplikowanie, ale jest on równowa˙zny szkol-nemu sposobowi mno˙zenia wielomianów, gdzie wyrazy (jednomiany) obu wielomianów wymna˙za si˛e ka˙zdy z ka˙zdym a nast˛epnie grupuje wyrazy według wykładników. Wielo-mianP (x) mo˙zna pomno˙zy´c przez stał ˛aa
a · P (x) =
n
X
i=0
a · aixi.
Przykład 1.1 NiechP (x) = x2+ 2x + 1 oraz Q(x) = 2x2+ x. Wtedy P (x) + Q(x) = 3x2+ 3x + 1
P (x) · Q(x) = 2x4+ 5x3+ 4x2+ x
1.3.1
Dzielenie wielomianów
Wielomiany mo˙zna te˙z dzieli´c. Mamy
Twierdzenie 1.2 Dla dowolnych dwóch wielomianówW (x) i V (x) istniej ˛a dwa wielo-mianyQ(x) i R(x) takie ˙ze
(a) W (x) = V (x) · Q(x) + R(x) (b) st(R(x)) < st(V (x))
WielomianQ(x) nazywamy ilorazem a R(x) reszt ˛a z dzieleniaW (x) przez V (x). Iloraz i reszta s ˛a wyznaczone jednoznacznie, to znaczy istnieje tylko jedna para Q(x), R(x) spełniaj ˛aca warunki (a) i (b).
Algorytm dzielenia wielomianów
Dane wej´sciowe: Dwa wielomianyW (x) = anxn+· · ·+a0orazV (x) = bmxm+· · ·+b0.
Zakładamy przy tym, ˙zean 6= 0 i bm 6= 0, czyli ˙ze W (x) jest stopnia n, a V (x) jest
stopniam.
Dane wyj´sciowe: ilorazQ(x) oraz reszta R(x)
(1) PodstawQ(x) := 0 oraz R(x) := W (x).
(2) Je˙zelist(R(x)) = n < m, to koniec, para Q(x), R(x) spełnia warunki (a) i (b).
(3) W przeciwnym przypadku powtarzaj co nast˛epuje dopókist(R(x)) ≥ m = st(V (x)):
(3.1) Niechckxkb˛edzie składnikiemR(x) z najwy˙zszym wykładnikiem.
(3.2) Podzielckxkprzezbmxm. (3.3) PodstawQ(x) := Q(x) + ck bmx k−m (3.4) PodstawR(x) := R(x) − ck bmx k−m· V (x)
Aby udowodni´c, ˙ze przedstawiony algorytm poprawnie oblicza iloraz i reszt˛e, poka˙ze-my, przez indukcj˛e, ˙ze warunek (a) jest spełniony po ka˙zdym kolejnym wykonaniu p˛etli (3). Na pocz ˛atku po wykonaniu kroku (1), welomianyQ(x) = 0 oraz R(x) = W (x)
spełniaj ˛a warunek (a). Oznaczmy warto´sci wielomianówQ(x) i R(x) przed i -tym
wy-konaniem p˛etli (3) przez Q1(x) i R1(x), a warto´sci po i -tym wykonanu p˛etli przez
Q2(x) i R2(x). Zakładamy przy tym, ˙ze W (x) = V (x) · Q1(x) + R1(x), ˙ze stopie´n
st(R1(x)) ≥ m, oraz ˙ze ckxkjest składnikiemR1(x) z najwie˛ekszym wykładnikiem. W
trakciei-tego wykonania p˛etli nast ˛api ˛a podstawienia
Q2(x) := Q1(x) + ck bm xk−m oraz R2(x) := R1(x) − ck bm xk−m· V (x). Mamy teraz R1(x) := ck bm xk−m· V (x) + R2(x) oraz W (x) = Q1(x)·V (x)+R1(x) = (Q1(x)+ ck bm xk−m)·V (x)+R 2(x) = Q2(x)·V (x)+R2(x),
czyliQ(x) oraz R(x) spełniaj ˛a warunek (a) poi tym wykonaniu p˛etli.
Zauwa˙zmy, ˙ze stopie ´n wielomianuR2(x) jest mniejszy od stopnia wielomianu R1(x),
poniewa˙z w wielomianieR2(x) = R1(x) −bcmkxk−m· V (x). współczynnik przy xk jest
równy0 i stopie´n st(R2(x)) < k. Tak wi˛ec p˛etla (3) nie mo˙ze si˛e wykonywa´c wi˛ecej ni˙z
n − m razy. Po wyj´sciu z p˛etli stopie´n st(R(x) < st(V (x)), czyli spełniony jest warunek
1.3. Wielomiany 7
Pokazali´smy wi˛ec, ˙ze wielomianW (x) mo˙zna przedstawi´c w postaci W (x) = Q(x) · V (x) + R(x) tak, ˙zeby st(R(x)) < st(V (x)). Teraz poka˙zemy, ˙ze iloraz Q(x) i reszta R(x) s ˛a wyznaczone jednoznacznie. Przypu´s´cmy bowiem, ˙ze
W (x) = Q1(x)V (x) + R1(x)
oraz
W (x) = Q2(x)V (x) + R2(x)
i ˙zest(R1(x)), st(R2(x)) < st(V (x)). Po odj˛eciu tych równo´sci stronami otrzymamy
0 = (Q1(x) − Q2(x))V (x) + (R1(x) − R2(x)).
Je˙zeli wielomianyQ1(x) 6= Q2(x), to wielomian (Q1(x) − Q2(x))V (x) ma stopie´n
wi˛ekszy lub równy odst(V (x)), a wielomian R1(x) − R2(x) ma stopie´n mniejszy od
st(V (x)), wi˛ec ich suma nie mo˙ze by´c wielomianem zerowym. Doszli´smy wi˛ec do
sprzecz-no´sci, czyliQ1(x) = Q2(x), z tego za´s wynika, ˙ze R1(x) = R2(x).
Przykład 1.3 Podzielmy wielomianW (x) = 8x3+6x2+3x+2 przez wielomian V (x) =
2x − 1 według opisanego wy˙zej algorytmu.
Najpierw w kroku (1) podstawiamyQ(x) := 0 oraz R(x) := 8x3+ 6x2+ 3x + 2.
Poniewa˙zst(R(x)) = 3 > 1 = st(V (x)) przechodzimy do p˛etli (3). Dzielimy składnik 8x3przez2x otrzymuj ˛ac4x2i podstawiamy
R(x) := R(x) − 4x2V (x) = 8x3+ 6x2+ 3x + 2 − 4x2(2x − 1) = 10x2+ 3x + 2. oraz
Q(x) := Q(x) + 4x2= 4x2.
Zauwa˙zmy, ˙ze spełniony jest warunekW (x) = Q(x) · V (x) + R(x).
Poniewa˙zst(R(x)) jest wi˛ekszy od 1 wykonujemy ponownie instrukcje p˛etli (3). Dzie-limy składnik10x2przez2x otrzymuj ˛ac5x i podstawiamy
R(x) := R(x) − 5xV (x) = 10x2+ 3x + 2 − 5x(2x − 1) = 8x + 2. oraz
Q(x) := Q(x) + 5x = 4x2+ 5x. (warunekW (x) = Q(x) · V (x) + R(x) jest spełniony).
Stopie´nst(R(x)) jest równy 1, wi˛ec wykonujemy ponownie instrukcje p˛etli (3). Dzie-limy składnik8x przez 2x otrzymuj ˛ac4 i podstawiamy
R(x) := R(x) − 4V (x) = 8x + 2 − 4(2x − 1) = 6. oraz
Q(x) := Q(x) + 4 = 4x2+ 5x + 4.
WarunekW (x) = Q(x) · V (x) + R(x) jest spełniony i teraz stopie´n st(R(x)) = 0 < 1 wi˛e algorytm ko´nczy prac˛e. WielomianQ(x) = 4x2+ 5x + 2 jest ilorazem a wielomian
1.3.2
Schemat Horna
Aby obliczy´c warto´s´c wielomianuP (x0) w jakim´s konkretnym punkcie x0mogliby´smy
bezpo´srednio skorzysta´c ze wzoruP (x0) =Pni=0aixi0. W ten sposób potrzebujemy, w
najgorszym przypadku, okołon2 mno˙ze´n. Istnieje jednak sposób wymagaj ˛acy tylkon
mno˙ze´n. Nale˙zy oblicza´c warto´s´c wielomianu według schematu
P (x0) = ((. . . (an· x0+ an−1) · x0+ an−2) · x0+ · · · a1) · x0+ a0.
Jest to tak zwany schemat Horna. Dokładniej mo˙zemy go przedstawi ´c nast˛epuj ˛aco:
Algorytm obliczania warto´sci wielomianu, schemat Horna
Dane wej´sciowe: współczynnikia0,a1, ... ,anwielomianuP (x) = an· xn+ · · · + a0
oraz argumentx0.
Dane wyj´sciowe: warto´s´c wielomianuy0= P (x0) = anxn0+ · · · + a1x0+ a0.
• y0:= an
• dla kolejnych i od 1 do n podstaw y0:= y0· x0+ an−i
1.3.3
Pierwiastki wielomianu
Pierwiastkiem wielomianuW (x) jest ka˙zda liczba rzeczywista a, która podstawiona do
wielomianu da warto´s´cW (a) = 0. Zachodzi
Twierdzenie 1.4 (Bézout) Liczbaa jest pierwiastkiem wielomianu W (x) wtedy i tylko wtedy, gdyW (x) dzieli si˛e przez x−a, czyli, gdy istnieje wielomian Q(x) taki, ˙ze W (x) = Q(x)(x − a).
Dowód: Je˙zeliW (x) = Q(x)(x − a), to W (a) = Q(a)(a − a) = 0.
Niech terazW (a) = 0. Podzielmy W (x) przez x − a, otrzymamy W (x) = Q(x)(x − a) + R(x)
przy czym stopie ´nR(x) jest mniejszy od 1, czyli jest stał ˛aR(x) = r. Wstawiaj ˛ac teraza
do obu stron otrzymamy
0 = Q(a)(a − a) + r,
czylir = 0 i W (x) = Q(x)(x − a). 2
Wniosek 1.5 Je˙zeli wielomian nie jest to˙zsamo´sciowo równy zero, to liczba jego
pier-wiastków nie jest wi˛eksza od jego stopnia.
Dowód: Niecha1,...,ak b˛ed ˛a ró˙znymi pierwiastkami wielomianuW (x). Z twierdzenia
Bézout mamy W (x) = Q1(x)(x − a1). Po podstawieniu a2 mamy 0 = W (a2) =
Q1(a2)(a2 − a1), czyli a2, jest pierwiastkiem wielomianuQ1(x). Korzystaj ˛ac znowu
z twierdzenia Bézout otrzymamyW (x) = Q2(x)(x − a2)(x − a1), i tak dalej. W ko´ncu
otrzymamy, ˙zeW (x) jest postaci W (x) = Q(x)(x − ak) · · · (x − a2)(x − a1), czyli
1.4. Zbiory 9
1.4
Zbiory
∅ oznacza zbiór pusty, który nie zawiera ˙zadnych elementów. N oznacza zbiór liczb naturalnych N= {0, 1, 2, 3, . . .}. Z oznacza zbiór liczb całkowitych.
Q oznacza zbiór liczb wymiernych. R oznacza zbiór liczb rzeczywistych.
a ∈ A oznacza, ˙ze elment a nale˙zy do zbioru A, a /∈ A, ˙ze elment a nie nale˙zy do
zbioruA. Najprostszy sposób zdefiniowania zbioru polega na wypisaniu jego elementów
w nawiasach klamrowych. Na przykład zbiór{1, 2, 3} zawiera elementy 1,2,3. Inny
spo-sób definiowania zbioru polega na podaniu własno´sci, któr¸a spełniaj¸a elementy zbioru. Na przykład{x | x ∈ N, 3 < x < 7} oznacza zbiór liczb naturalnych wi¸ekszych od 3 i
mniejszych od 7.
|A| oznacza moc zbioru A, czyli liczb¸e jego elementów. |{3, 6, 9}| = 3, |∅| = 0.
A ∪ B oznacza sum¸e zbiorów, czyli zbiór, który zawiera elementy, które nale˙z ˛a doA lub
doB:
A ∪ B = {x : x ∈ A lub x ∈ B}.
A zatem sumaA ∪ B zawiera wszystkie elementy zbioru A i wszystkie elementy zbioru B.
A ∩ B oznacza iloczyn lub przekrój zbiorów, czyli zbiór, który zawiera te elementy,
które nale˙z¸a do obu zbiorów naraz.
A ∩ B = {x : x ∈ A i x ∈ B}.
A − B oznacza ró˙znic¸e zbiorów, czyli zbiór, który zawiera te elementy, które nale˙z¸a
doA i nie nale˙z¸a do B.
A − B = {x : x ∈ A i x /∈ B}.
Przykład 1.6 DlaA = {1, 2, 4} i B = {1, 4, 6} mamy:
A ∪ B = {1, 2, 4, 6}, A ∩ B = {1, 4}, A − B = {2}.
A ⊆ B oznacza, ˙ze zbior A zawiera si¸e w zbiorze B, to znaczy wszystkie elementy zbioru A nale˙z¸a do zbioru B.
{2, 1} ⊆ {1, 2, 3}
Dwa zbiory s¸a równe je˙zeli zawieraj¸a te same elementy, lub inaczejA = B wtedy i tylko
wtedy gdyA ⊆ B i B ⊆ A.
{1, 4, 2, 3} = {4, 1, 3, 2}.
Jak wida´c kolejno´s´c elementów w zapisie zbioru nie ma znaczenia. I tak na przykład
{1, 2} = {2, 1}. Taki zbiór dwuelementowy nazywamy par¸a nieuporz¸adkowan¸a.
W poni˙zszym lemacie zebrano podstawowe własno´sci operacji sumy i iloczynu zbio-rów.
Lemat 1.7 • A ∪ B = B ∪ A (przemienno´s´c sumy). • A ∩ B = B ∩ A (przemienno´s´c iloczynu).
• A ∪ (B ∪ C) = (A ∪ B) ∪ C (ł¸aczno´s´c sumy). • (A ∩ B) ∩ C = A ∩ (B ∩ C) (ł¸aczno´s´c iloczynu).
• (A ∪ B) ∩ C = A ∩ C ∪ B ∩ C (rozdzielno´s´c sumy wzgl¸edem iloczynu). • (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) (rozdzielno´s´c iloczynu wzgl¸edem sumy). • A ∪ ∅ = A, A ∩ ∅ = ∅, A ∪ A = A, A ∩ A = A,
Dowód: Udowodnimy tylko rozdzielno´s´c sumy wzgl¸edem iloczynu. W tym celu
poka˙ze-my dwa zawierania:(A ∪ B) ∩ C ⊂ A ∩ C ∪ B ∩ C oraz A ∩ C ∪ B ∩ C ⊂ (A ∪ B) ∩ C.
Aby udowodni´c zawieranie(A ∪ B) ∩ C ⊂ A ∩ C ∪ B ∩ C, we˙zmy dowolny element x ∈ (A ∪ B) ∩ C, wtedy x ∈ A ∪ B oraz x ∈ C, a to oznacza, ˙ze x nalezy do C i do
jednego ze zbiorówA lub B (lub do obu), czyli nale˙zy do A ∩ C lub do B ∩ C, a wi˛ec x ∈ A ∩ C ∪ B ∩ C. Pokazali´smy wi˛ec, ˙ze dowolny element z (A ∪ B) ∩ C nale˙zy do A ∩ C ∪ B ∩ C.
Aby udowodni´c zawieranieA ∩ C ∪ B ∩ C ⊂ (A ∪ B) ∩ C. we˙zmy dowolny element x ∈ A ∩ C ∪ B ∩ C, wtedy x ∈ A ∩ C lub x ∈ B ∩ C, a to oznacza, ˙ze x nalezy do C
i do jednego ze zbiorówA lub B (lub do obu), czyli nale˙zy do A ∪ B oraz do C, a wi˛ec x ∈ (A ∪ B) ∩ C. Pokazali´smy wi˛ec, ˙ze dowolny element z A ∩ C ∪ B ∩ C nale˙zy do
(A ∪ B) ∩ C. 2
1.5
Ró˙znica symetryczna zbiorów
A ⊕ B oznacza ró˙znic¸e symetryczn¸a zbiorów, która zawiera elementy nale˙z¸ace tylko do
jednego z dwóch zbiorów:
A ⊕ B = (A − B) ∪ (B − A).
Przykład 1.8
{1, 2, 4} ⊕ {1, 4, 6} = {2, 6}.
W poni˙zszym lemacie zebrano podstawowe własno´sci ró˙znicy symetrycznej zbiorów.
Lemat 1.9 • A ⊕ B = B ⊕ A (przemienno´s´c). • (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C) (ł¸aczno´s´c).
• (A ⊕ B) ∩ C = A ∩ C ⊕ B ∩ C (rozdzielno´s´c wzgl¸edem iloczynu). • A ⊕ ∅ = A, A ⊕ A = ∅.
1.6. Iloczyn kartezja ´nski 11
Dowód:
Udowodnimy, tylko dwie to˙zsamo´sci, dowód pozostałych pozostawiamy czytelnikowi jako ´cwiczenie.
Aby pokaza´c, ˙ze ró˙znica symetryczna jest ł ˛aczna wystarczy zauwa˙zy ´c, ˙ze zbiórA ⊕ (B⊕C) lub (A⊕B)⊕C zawiera te elementy, które nale˙z¸a do nieparzystej liczby zbiorów,
czyli te, które nale˙z¸a tylko doA, plus te, które nale˙z¸a tylko do B, plus te, które nale˙z¸a
tylko doC, plus te, które nale˙z¸a do przekroju A ∩ B ∩ C.
Udowodnimy teraz ostatni ˛a implikacj˛e. Je˙zeliA ⊕ B = ∅, to
A = A ⊕ ∅ = A ⊕ (A ⊕ B) = (A ⊕ A) ⊕ B = ∅ ⊕ B = B.
2
Twierdzenie 1.10 Ró˙znica symetrycznan zbiorów: A1⊕ A2⊕ . . . ⊕ An
zawiera elementy, które nale˙z¸a do nieparzystej liczby spo´sród zbiorówA1,A2, . . . , An.
Dowód przez indukcj¸e ze wzgl¸edu nan. Twierdzenie jest oczywiste dla n = 1 lub n = 2. Załó˙zmy teraz, ˙ze jest ono prawdziwe dla n i rozpatrzmy:
A1⊕ . . . ⊕ An⊕ An+1= (A1⊕ . . . ⊕ An) ⊕ An+1.
Zbiór ten zawiera te elementy, które nale˙z¸a do(A1⊕ . . . ⊕ An) i nie nale˙z¸a do An+1,
oraz te, które nie nale˙z¸a do(A1⊕ . . . ⊕ An) i nale˙z¸a do An+1. W pierwszym
przypad-ku s¸a to elementy, które nie nale˙z¸a doAn+1 i na mocy zało˙zenia indukcyjnego nale˙z¸a
do jakiej´s nieparzystej liczby zbiorów spo´sródA1, . . . , An. W drugim przypadku s¸a to
elementy, które nale˙z¸a doAn+1, a tak˙ze do pewnej parzystej liczby zbiorów spo´sród
A1, . . . , An. Razem mamy wszystkie elementy nale˙z¸ace do nieparzystej liczby zbiorów
spo´sródA1, . . . , An+1. 2
1.6
Iloczyn kartezja ´nski
Para uporz¸adkowana jest to dwuelementowy ci ˛ag(x, y). Mamy (x, y) = (u, v) wtedy i
tylko wtedy gdyx = u oraz y = v. Dopuszczalne jest tak˙ze x = y.
A×B oznacza iloczyn kartezja´nski zbiorów A i B. Jest to zbiór wszystkich uporz¸adkowanych
par(a, b), w których a ∈ A i b ∈ B. Inaczej
A × B = {(a, b) | a ∈ A, b ∈ B}.
Przykład 1.11 DlaA = {1, 3, 5} i B = {3, 4} mamy
A × B = {(1, 3), (1, 4), (3, 3), (3, 4), (5, 3), (5, 4)}.
Mo˙zna łatwo wykaza´c, ˙ze
1.7
Rodzina zbiorów
Czasami b˛edziemy mieli do czynienia ze zbiorem, którego elementami s ˛a zbiory. Przez
P(A) lub 2A
b˛edziemy oznacza´c zbiór wszystkich podzbiorów zbioruA.
Przykład 1.12 DlaA = {a, b}
P(A) = {∅, {a}, {b}, {a, b}}.
Zbiór zbiorów nazywamy czasami rodzin¸a zbiorów. Na przykładA = {A1, A2, A3, A4}
jest rodzin¸a zawieraj¸ac¸a cztery zbioryA1,A2,A3iA4, s¸a to elementy zbioruA. Mo˙zemy
te˙z zapisa´cA = {Ai| 1 ≤ i ≤ 4}.
Mo˙zemy sumowa´c zbiory z rodziny. Suma
k
[
i=1
Ai
zawiera te elementy, które nale˙z¸a do którego´s ze zbiorówA1,A2, ... ,Ak, czyli k
[
i=1
Ai= {x | ∃i1≤i≤kx ∈ Ai}.
Inaczej mo˙zemy to zapisa´c:
k
[
i=1
Ai= A1∪ A2∪ . . . ∪ Ak.
B¸edziemy te˙z u˙zywa´c zapisu
[
i∈I
Ai
na oznaczenie sumy wszystkich zbiorówAi, których indeksy nale˙z¸a do zbioruI.
Zacho-dzi wtedy
[
i∈I
Ai= {x | ∃i∈I x ∈ Ai}.
Zbiór indeksów sumowania mo˙ze by´c okre´slony za pomoc¸a warunku.
[
1<i<6
Ai= A2∪ A3∪ A4∪ A5.
Dla sumy zbiorów zachodzi prawo rozdzielno´sci sumy wzgl˛edem przekroju:
Lemat 1.13 C ∩[ i∈I Ai= [ i∈I (C ∩ Ai)
1.7. Rodzina zbiorów 13
Dowód: We´zmy dowolny elementx ∈ C ∩S
i∈IAi. Wtedyx nale˙zy do C i do którego´s
ze zbiorówAi, czyli dla jakiego´si ∈ I, x nale˙zy do C ∩Ai, a to znaczy, ˙zex ∈Si∈I(C ∩
Ai).
We´zmy z kolei dowolny elementx ∈ S
i∈I(C ∩ Ai). Wtedy x nale˙zy do C ∩ Ai
dla jakiego´si ∈ I, czyli x nale´zy do C i do sumy S
i∈IAi, czyli nale˙zy do przekroju
C ∩S
i∈IAi. 2
Mo˙zemy te˙z bra´c przekroje zbiorów z rodziny. Przekrój
k
\
i=1
Ai
zawiera te elementy, które nale˙z¸a do wszystkich zbiorówA1,A2, ... ,Ak, czyli k
\
i=1
Ai= {x | ∀i1≤i≤kx ∈ Ai}.
Inaczej mo˙zemy to zapisa´c:
k
\
i=1
Ai = A1∩ A2∩ . . . ∩ Ak.
B¸edziemy te˙z u˙zywa´c zapisu
\
i∈I
Ai
na oznaczenie przekroju wszystkich zbiorówAi, których indeksy nale˙z¸a do zbioruI.
Zachodzi wtedy
\
i∈I
Ai= {x | ∀i∈I x ∈ Ai}.
Zbiór indeksów przekroju mo˙ze by´c okre´slony za pomoc¸a warunku:
\
1<i<6
Ai = A2∩ A3∩ A4∩ A5.
Przykład 1.14 We´zmy rodzin¸e zło˙zon¸a z trzech zbiorówA1 = {4, 6, 8}, A2= {4, 5, 6},
A3= {4, 5, 8, 9}. 3 [ i=1 Ai = {4, 5, 6, 8, 9}, 3 \ i=1 Ai= {4}.
Przykład 1.15 NiechI = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} b¸edzie zbiorem indeksów. Dla ka˙z-degoi ∈ I okre´slamy zbór Ai= {x ∈ N | 1 ≤ x ≤ i}. Mamy:
[ i∈I Ai= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, \ i∈I Ai= {1}, [ 1<i<7 Ai = {1, 2, 3, 4, 5, 6}, \ 1<i<7 Ai= {1, 2}.
1.8
Grafy (nieskierowane)
Definicja 1.16 Graf (nieskierowany)G = (VG, EG) jest to para składaj¸aca si¸e ze
sko´n-czonego zbioru wierzchołkówVG oraz ze zbioru kraw¸edziEG, gdzie kraw¸edzie to pary
wierzchołków.
EG⊆ {{u, v} | u, v ∈ VG, u 6= v}.
O kraw¸edzie = {u, v} mówimy, ˙ze ł¸aczy wierzchołki u i v, a o wierzchołkach u i v, ˙ze
s¸a ko´ncami kraw¸edzie. Wierzchołki poł ˛aczone kraw˛edzi ˛a nazywamy s ˛asiednimi. Stopie´n
wierzchołkav, oznaczany przez d(v), jest to liczba kraw¸edzi wychodz¸acych z v.
Graf przedstawiamy na rysunku jako zbiór punktów (lub kółek) poł¸aczonych odcin-kami (lub łuodcin-kami).
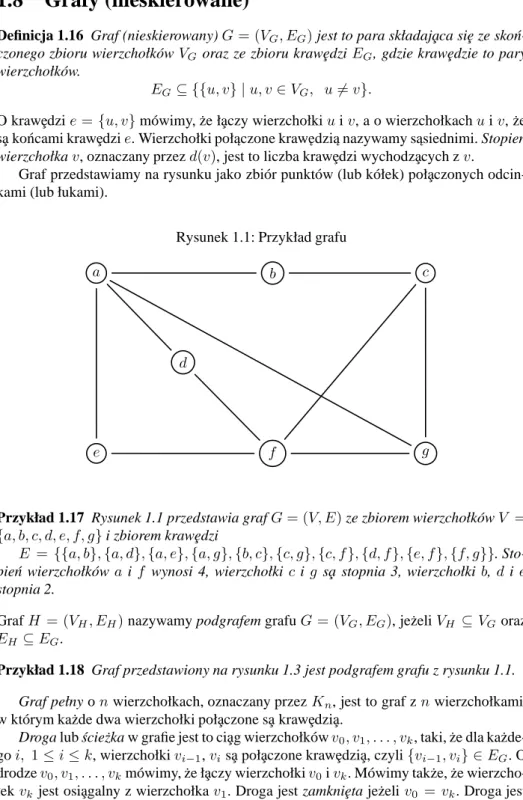
Rysunek 1.1: Przykład grafu
a b c
d
e f g
Przykład 1.17 Rysunek 1.1 przedstawia grafG = (V, E) ze zbiorem wierzchołków V = {a, b, c, d, e, f, g} i zbiorem kraw¸edzi
E = {{a, b}, {a, d}, {a, e}, {a, g}, {b, c}, {c, g}, {c, f }, {d, f}, {e, f}, {f, g}}. Sto-pie´n wierzchołkówa i f wynosi 4, wierzchołki c i g s¸a stopnia 3, wierzchołki b, d i e stopnia 2.
GrafH = (VH, EH) nazywamy podgrafem grafu G = (VG, EG), je˙zeli VH ⊆ VG oraz
EH⊆ EG.
Przykład 1.18 Graf przedstawiony na rysunku 1.3 jest podgrafem grafu z rysunku 1.1.
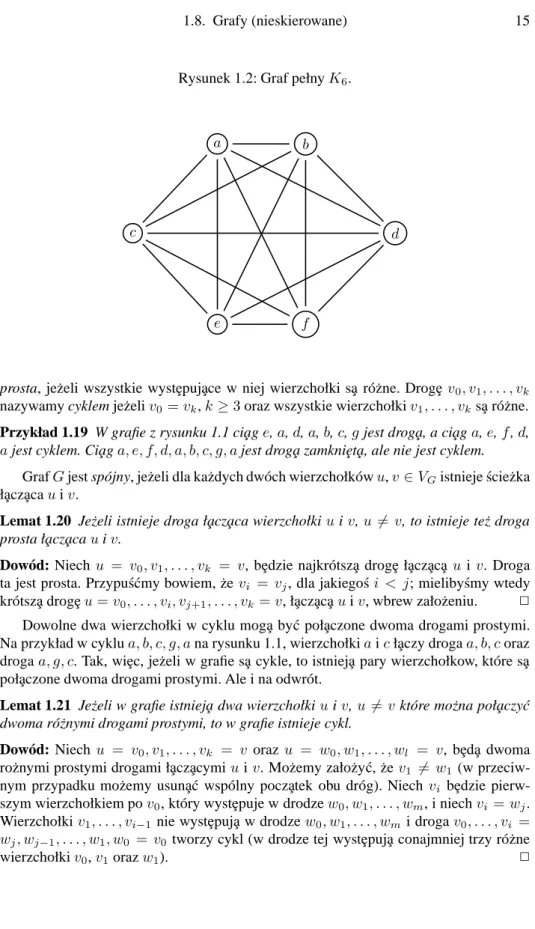
Graf pełny on wierzchołkach, oznaczany przez Kn, jest to graf zn wierzchołkami,
w którym ka˙zde dwa wierzchołki poł¸aczone s¸a kraw¸edzi¸a.
Droga lub ´scie˙zka w grafie jest to ci¸ag wierzchołkówv0, v1, . . . , vk, taki, ˙ze dla
ka˙zde-goi, 1 ≤ i ≤ k, wierzchołki vi−1,vis¸a poł¸aczone kraw¸edzi¸a, czyli{vi−1, vi} ∈ EG. O
drodzev0, v1, . . . , vkmówimy, ˙ze ł¸aczy wierzchołkiv0ivk. Mówimy tak˙ze, ˙ze
1.8. Grafy (nieskierowane) 15
Rysunek 1.2: Graf pełnyK6.
a b
c d
e f
prosta, je˙zeli wszystkie wyst¸epuj¸ace w niej wierzchołki s¸a ró˙zne. Drog¸ev0, v1, . . . , vk
nazywamy cyklem je˙zeliv0= vk,k ≥ 3 oraz wszystkie wierzchołki v1, . . . , vks¸a ró˙zne.
Przykład 1.19 W grafie z rysunku 1.1 ci¸age, a, d, a, b, c, g jest drog¸a, a ci¸ag a, e, f , d, a jest cyklem. Ci¸ag a, e, f, d, a, b, c, g, a jest drog¸a zamkni¸et¸a, ale nie jest cyklem.
GrafG jest spójny, je˙zeli dla ka˙zdych dwóch wierzchołków u, v ∈ VGistnieje ´scie˙zka
ł¸acz¸acau i v.
Lemat 1.20 Je˙zeli istnieje droga ł¸acz¸aca wierzchołkiu i v, u 6= v, to istnieje te˙z droga prosta ł¸acz¸acau i v.
Dowód: Niechu = v0, v1, . . . , vk = v, b¸edzie najkrótsz¸a drog¸e ł¸acz¸ac¸a u i v. Droga
ta jest prosta. Przypu´s´cmy bowiem, ˙zevi = vj, dla jakiego´si < j; mieliby´smy wtedy
krótsz¸a drog¸eu = v0, . . . , vi, vj+1, . . . , vk= v, ł¸acz¸ac¸a u i v, wbrew zało˙zeniu. 2
Dowolne dwa wierzchołki w cyklu mog¸a by´c poł¸aczone dwoma drogami prostymi. Na przykład w cyklua, b, c, g, a na rysunku 1.1, wierzchołki a i c ł¸aczy droga a, b, c oraz
drogaa, g, c. Tak, wi¸ec, je˙zeli w grafie s¸a cykle, to istniej¸a pary wierzchołkow, które s¸a
poł¸aczone dwoma drogami prostymi. Ale i na odwrót.
Lemat 1.21 Je˙zeli w grafie istniej¸a dwa wierzchołkiu i v, u 6= v które mo˙zna poł¸aczy´c dwoma ró˙znymi drogami prostymi, to w grafie istnieje cykl.
Dowód: Niechu = v0, v1, . . . , vk = v oraz u = w0, w1, . . . , wl = v, b¸ed¸a dwoma
ro˙znymi prostymi drogami ł¸acz¸acymiu i v. Mo˙zemy zało˙zy´c, ˙ze v1 6= w1(w
przeciw-nym przypadku mo˙zemy usun¸a´c wspólny pocz¸atek obu dróg). Niechvi b¸edzie
pierw-szym wierzchołkiem pov0, który wyst¸epuje w drodzew0, w1, . . . , wm, i niechvi = wj.
Wierzchołkiv1, . . . , vi−1 nie wyst¸epuj¸a w drodzew0, w1, . . . , wmi drogav0, . . . , vi =
wj, wj−1, . . . , w1, w0 = v0tworzy cykl (w drodze tej wyst¸epuj¸a conajmniej trzy ró˙zne
Z tego lematu wynika, ˙ze graf jest acykliczny (nie ma cykli) wtedy i tylko wtedy, gdy ka˙zde dwa wierzchołki grafu mo˙zna poł¸aczy´c co najwy˙zej jedn¸a drog¸a prost¸a.
1.9
Drzewa
Definicja 1.22 Spójny i acykliczny (bez cykli) graf to drzewo.
Rysunek 1.3: Przykład drzewa
a b c
d
e f g
Z rozwa˙za´n z poprzedniego podrozdziału wynika:
Lemat 1.23 Graf jest drzewem wtedy i tylko wtedy, gdy ka˙zde dwa jego wierzchołki
mo˙z-na poł¸aczy´c dokładnie jedn¸a prost¸a drog¸a.
1.10
Drzewa ukorzenione
Definicja 1.24 Drzewo ukorzenione to drzewo z wyró˙znionym jednym wierzchołkiem.
Wyró˙zniony wierzchołek nazywamy korzeniem drzewa.
Ka˙zdy wierzchołekv ró˙zny od korzenia jest z nim poł ˛aczony dokładnie jedn ˛a drog ˛a prost ˛a. S ˛asiad le˙z ˛acy na drodze do korzenia nazywamy ojcem wierzchołkav. Pozastali
s ˛asiedzi s ˛a synami wierzchołkav. Korze ´n drzewa nie ma ojca, wszyscy jego s ˛asiedzi s ˛a jego synami. Wierzchołek, który nie posiada syna nazywamy li´sciem.
Przykład 1.25 Je˙zeli w drzewie z rysunku 1.3 wyró˙znimy wierzchołeka jako korze´n, to ojcem wierzchołkad jest wierzchołek a, synem wierzchołka d jest wierzchołek f . Wierz-chołkic, e, f oraz g s ˛a li´sciami.
Zwykle drzewo ukorzenione rysujemy w ten sposób, ˙ze korze ´n jest na górze, poni-˙zej le˙z ˛a jego synowie i ogólnie ka˙zdy wierzchołek le˙zy poni˙zej swojego ojca i powy˙zej swoich synów.
1.11. Grafy skierowane 17
1.11
Grafy skierowane
Definicja 1.26 Graf skierowany (zorientowany) to dowolna paraG = (V, E), ze sko´n-czonym zbiorem wierzchołkówV i zbiorem kraw¸edzi E ⊆ V × V .
Rysunek 1.4: Graf skierowany
a b c
d e
W grafie skierowanym kraw¸ed´ze = (u, v) jest skierowana od wierzchołka u do
wierz-chołkav. Wierzchołek u nazywamy pocz¸atkiem kraw¸edzi, a wierzchołek v ko ´ncem. Na
rysunkach kraw¸edzie skierowane b¸edziemy przedstawia ´c jako strzałki. Droga w grafie skierowanym jest to ci¸ag wierzchołkówv0, v1, . . . , vk, taki, ˙ze dla ka˙zdegoi, 1 ≤ i ≤ k,
wierzchołkivi−1,vis¸a poł¸aczone kraw¸edzi¸a, czyli(vi−1, vi) ∈ E. Kraw¸ed´z typu (u, u),
w której pocz¸atek i koniec pokrywaj¸a si¸e, nazywamy p¸etl¸a.
1.12
Słowa
Słowa s ˛a to ci ˛agi liter lub symboli z jakiego´s sko´nczonego zbioruΣ. Zbiór Σ nazywamy
wtedy alfabetem. Zbiór wszystkich słów nad alfabetemΣ oznaczamy przez Σ∗.
W´sród słów wyró˙zniamy słowo pusteλ, które nie zawiera ˙zadnych liter.
Przykład 1.27 Na przykład, je˙zeliΣ = {a, b}, to Σ∗zawiera słowo pusteλ, dwa słowa
jednoliterowea i b, cztery słowa dwuliterowe aa, ab, ba i bb, osiem słów trzyliterowych aaa, aab, aba i abb, baa, bab, bba i bbb, i tak dalej.
Długo´s´c słowaw ∈ Σ jest to liczba jego liter, b˛edziemy j ˛a oznacza ´c przez|w|.
Dłu-go´s´c słowa pustego|λ| = 0. Zbiór wszystkich słów długo´sci n nad alfabetem Σ
oznacza-my przez
Σn.
Dla słów mo˙zemy okre´sli´c operacj˛e konkatenacji, lub składania słów. Konkatenacja (lub
zło˙zenie) dwóch słówu, v ∈ Σ, oznaczana przez uv, jest to sklejenie słów u i v. Do słowa u dopisujemy na ko´ncu słowo v. Dla dowolnego słowa v ∈ Σ∗zachodziλv = vλ = v.
Słowou jest prefiksem lub przedrostkiem słowa v, je˙zeli istnieje takie słowo w, ˙ze v = uw. Podobnie, słowo u jest sufiksem lub przyrostkiem słowa v, je˙zeli istnieje takie
słowow, ˙ze v = wu.
Przykład 1.29 Na przykładaba jest prefiksem słowa abaaab, a słowo ab jest sufiksem słowaabaaab. Słowo puste jest prefixem i sufiksem dowolnego słowa v. Ka˙zde słowo v jest swoim własnym prefiksem i sufiksem.
Zwykle alfabet jest zbiorem uporz ˛adkowanym, lub mówi ˛ac inaczej mamy pewn ˛a ko-lejno´s´c liter w alfabecie. Na przykład w zbiorzeΣ = {a, b} litera a stoi przed b. Mo˙zemy
wtedy uporz ˛adkowa´c zbiór słów nad alfabetemΣ.
Jeden porz ˛adek nazywa si˛e porz ˛adkiem leksykograficznym. Jest to porz ˛adek słów w słownikach. Aby porówna´c dwa słowau, v ∈ Σ, szukamy pierwszej pozycji, na której te
dwa słowa si˛e ró˙zni ˛a. Słowo, które ma na tej pozycji wcze´sniejsz ˛a liter˛e, jest wcze´sniejsze w porz ˛adku leksykograficznym. Je˙zeli takiej pozycji nie ma, to albou = v, albo jedno
ze słów jest prefiksem drugiego, wtedy wcze´sniejszy w porz ˛adku leksykograficznym jest prefiks.
Przykład 1.30 W porz ˛adku leksykograficznym słowoab jest wcze´sniejsze od słowa ababa, a to jest wcze´sniejsze odabb.
Porz ˛adek leksykograficzny jest wygodny, je˙zeli zbiór słów jest sko ´nczony. Zauwa˙zmy, ˙ze w zbiorze wszystkich słów{a, b}∗ niesko´nczenie wiele słów (wszystkie słowa zło˙zone
tylko z literya) poprzedza słowo b. Dlatego czasami stosuje si˛e inny porz ˛adek, tak zwany
porz ˛adek kanoniczny.
Słowou poprzedza słowo v w porz ˛adku kanonicznym, je˙zeli:
• albo |u| < |v|,
• albo |u| = |v| i u poprzedza v w porz ˛adku leksykograficznym.
Przykład 1.31 Pocz ˛atkowe słowa zbioru{a, b}∗uporz ˛adkowane według porz ˛adku
kano-nicznego to:
λ, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, bbb, aaaa, . . .
1.13
Zaokr¸aglenia
Wprowad´zmy dwa oznaczenia na zaokr¸aglenie liczby rzeczywistej. Dla dowolnej liczby rzeczywistejx
dxe oznacza zaokr¸aglenie x w gór¸e do najbli˙zszej liczby całkowitej. bxc oznacza zaokr¸aglenie x w dół do najbli˙zszej liczby całkowitej.
Zaokr ˛agleniedxe nazywamy sufitem z x, a zaokr ˛agleniebxc nazywamy podłog ˛a zx.
Przykład 1.32
d4e = 4, d4.3e = 5, d−4e = −4, d−4.3e = −4. b4c = 4, b4.3c = 4, b−4c = −4, b−4.3c = −5.
1.14. Przedrostki 19
1.14
Przedrostki
W przypadku bardzo du˙zych lub bardzo małych warto´sci u˙zywa si¸e czasami jednostek miar b¸ed¸acych wielokrotno´sciami lub podwielokrotno´sciami podstawowych jednostek. Takie jednostki wyra˙za si¸e przez dodanie do nazwy jednostki odpowiedniego przedrostka, a do oznaczenia tej jednostki dodaje si¸e oznaczenie przedrostka. W nast¸epuj¸acej tabeli zebrano te przedrostki.
Przedrostek Oznaczenie Wielokrotno´s´c
exa E 1018 peta P 1015 tera T 1012 giga G 109 mega M 106 kilo k 103 hekto h 102 deka da 10
Przedrostek Oznaczenie Podwielokrotno´s´c
decy d 10−1 centy c 10−2 mili m 10−3 mikro µ 10−6 nano n 10−9 piko p 10−12 femto f 10−15 atto a 10−18
Przykładami tak utworzonych jednostek s¸a: centymetr (cm), milimetr (mm), hehtopa-skal, hektolitr, kilogram (kg), kilowat (kW). Do mierzenia pr¸edko´sci (zegara) procesora u˙zywa si¸e megahertzów. Jeden megahertz (MHz) to jednostka cz¸esto´sci równa miliono-wi impulsów na sekund¸e. Kilobajtów, megabajtów i gigabajtów u˙zywa si¸e do mierzenia liczby komórek pami¸eci. Cz¸esto przyjmuje si¸e, ˙ze kilobajt ma 1024 bajtów, megabajt 1024 × 1024 bajtów, a gigabajt 1024 × 1024 × 1024 bajtów.
1.15
Notacja asymptotyczna
W analizie jakiego´s algorytmu (programu) wa˙zne jest oszacowanie jego czasu działania. Jako przykład we´zmy algorytm sortowania b ˛abelkowego, który ustawia elementy ci ˛agu wej´sciowego w porz ˛adku niemalej ˛acym.
Algorytm sortowania b ˛abelkowego.
Aby posortowa´c ci ˛ag długo´scin:
(1) wykonujemy co nast˛epujen − 1 razy:
(1b) wykonujemy co nast˛epujen − 1 razy:
porównujemy wskazany element z elementem nast˛epnym,
je˙zeli porównane elementy s ˛a w niewła´sciwej kolejno´sci, to zamieniamy je miejscami,
wskazujemy na nast˛epny element.
W poni˙zszej tabeli zilustrowano zastosowanie algorytmu dla ci ˛agu(3, 4, 1, 2). ˆ 3 4 1 2 3 ˆ4 1 2 3 1 ˆ4 2 ˆ 3 1 2 4 1 ˆ3 2 4 1 2 ˆ3 4 ˆ 1 2 3 4 1 ˆ2 3 4 1 2 ˆ3 4
Kolejne wiersze przedstawiaj ˛a ci ˛ag po kolejnych porównaniach. Element aktualnie wska-zany jest zaznaczony daszkiem.
Poprawno´s´c powy˙zszego algorytmu wynika z faktu, ˙ze po pierwszym wykonaniu ze-wn˛etrznej p˛etli (1) najwi˛ekszy element ci ˛agu znajdzie si˛e na ko ´ncu, po drugim wykonaniu p˛etli drugi najwi˛ekszy element ci ˛agu znajdzie si˛e na przedostatniej pozycji, i tak dalej. Po ka˙zdym kolejnym wykonaniu p˛etli (1) kolejny najwi˛ekszy element znajdzie swoj ˛a wła-´sciw ˛a pozycj˛e.
Czas działania algorytmu zale˙zy odn — liczby elementów w ci ˛agu. P˛etla zewn˛etrzna (1) jest wykowywanan−1 razy. W ka˙zdej iteracji p˛etli zewn˛etrznej p˛etla wewn˛etrzna (1b)
równie˙z jest wykonywanan − 1 razy. W ka˙zdym kolejnym wykonaniu p˛etli wewn˛etrznej
algorytm wykonuje kilka kroków. Tak wi˛ec, aby posortowa ´c ci ˛ag długo´scin algorytm w
sumie wykonujec(n − 1)2kroków, gdziec jest pewn ˛a stał ˛a.
Czas pracy powy˙zszego algorytmu został oszacowany z dokładno´sci ˛a do stałej. Jest to powszechna praktyka i b˛edziemy tak post˛epowa´c w tej ksi ˛a˙zce.
Do szacowania czasu pracy algorytmu (jego zło˙zono´sci czasowej) i do porównywania algorytmów pod wzgl˛edem czasu działania b˛edziemy u˙zywa ´c notacji asymptotycznej.
Niechf i g b˛ed ˛a dwiema funkcjami okre´slonymi na zbiorze liczb naturalnych o war-to´sciach w zbiorze dodatnich liczb rzeczywistych
f, g : N → {x|x ∈ R, x > 0}.
Wtedy:
• g(n) = O(f (n)), je˙zeli istnieje dodatnia stała c > 0 taka, ˙ze g(n) ≤ c · f (n)
dla prawie wszystkichn ∈ N, to znaczy istnieje n0, takie, ˙zeg(n) ≤ c · f (n) dla
1.15. Notacja asymptotyczna 21
• g(n) = o(f (n)), je˙zeli limn→∞g(n)f(n) = 0. W takim przypadku mówimy, ˙ze
funk-cjag jest o małe od f .
• g(n) = Ω(f (n)), je˙zeli istnieje dodatnia stała c > 0 taka, ˙ze g(n) ≥ c · f (n) dla
prawie wszystkichn ∈ N. W takim przypadku mówimy, ˙ze funkcja g jest Omega du˙ze odf .
• g(n) = Θ(f (n)), je˙zeli istniej ˛a dwie dodatnie stałec1, c2> 0 takie, ˙ze c1· f (n) ≤
g(n) ≤ c2· f (n) dla prawie wszystkich n ∈ N. W takim przypadku mówimy, ˙ze
funkcjag jest Theta du˙ze od f .
Je˙zelig(n) = O(f (n)), to mówimy, ˙ze funkcja f ogranicza z góry funkcj˛e g(n) (z
dokładno´sci ˛a do stałej), albo, ˙ze rz ˛ad funkcjig jest nie wi˛ekszy od rz˛edu funkcji f .
Przykład 1.33
• Czas działania algorytmu sortowania b ˛abelkowego jestO(n2).
• n = O(3n − 2). • 3n − 2 = O(n). • n3+ n2− n = O(n3).
• n3= O(2n).
• n2log n = O(n3).
B˛edziemy dopuszcza´c notacj˛e asymptotyczn ˛a tak˙ze wobec funkcji, które s ˛a dodatnie dla prawie wszystkich liczb naturalnych. Na przykładn2− 3n = O(n2).
Je˙zelig(n) = o(f (n)), to mówimy, ˙ze g jest ni˙zszego rz˛edu ni˙z f .
Przykład 1.34
• n2= o(n3).
• n = o(n log n). • n3= o(2n).
Je˙zelig(n) = Θ(f (n)), to g i f s ˛a tego samego rz˛edu, czylig(n) = O(f (n)) oraz f (n) = O(g(n)).
Przykład 1.35
• n2= Θ(n2+ n).
• n = Θ(n + log n).
Nast˛epuj ˛acy lemat jest bardzo u˙zyteczny przy szacowaniu asymptotycznym. Jego do-wód zostawiamy jako ´cwiczenie.
Lemat 1.36 Je˙zeli granicalimg(n)f(n)istnieje i jest wła´sciwa (nie jest równa∞), to g(n) = O(f (n)).
Wniosek 1.37 Je˙zelig(n) = o(f (n)), to g(n) = O(f (n)).
Nast˛epuj ˛acy przykład pokazuje, ˙ze oszacowanie asymptotyczne mo˙ze by ´c zawodne.
Przykład 1.38 We´zmy dwie funkcjef (n) = 300n oraz g(n) = n log2n. Mamy f (n) =
o(g(n)), ale f (n) ≥ g(n) dla wszystkich n ≤ 2300, czyli dla wszystkich liczb mniejszych
od liczby atomów w naszej galaktyce (porównaj podrozdział du˙ze liczby w rozdziale o arytmetyce).
Z drugiej jednak strony oszacowanie asymptotyczne wystarczy do naszych celów i jest łatwiejsze do uzyskania.
Przykład 1.39 Rozwa˙zmy trzy algorytmy: pierwszy działaj ˛acy w czasief1(n) = c1n,
drugi w czasief2(n) = c2n3 i trzeci w czasief3(n) = c32n. Funkcje te okre´slaj ˛a czas
działania na pewnym konkretnym komputerze. Niech n1, n2 i n3 oznazczaj ˛a długo´sci
wej´s´c, dla których algorytmy daj ˛a odpowied´z w ci ˛agu jednej sekundy, to znaczyf1(n1) =
f2(n2) = f3(n3) = 1s.
Przypu´s´cmy teraz, ˙ze mamy 1000 razy szybszy komputer i pytamy jakie wej´scia teraz mog ˛a by´c policzone przez te algorytmy w ci ˛agu jednej sekundy.
Dla pierwszego algorytmu działaj ˛acego w czasie liniowym mo˙zemy teraz oblicza´c 1000 razy dłu˙zsze dane wej´sciowe, poniewa˙zf1(1000n1) = 1000f1(n1). Dla
drugie-go aldrugie-gorytmu działaj ˛acego w czasie sze´sciennym mo˙zemy teraz oblicza´c 10 razy dłu˙zsze dane wej´sciowe, poniewa˙zf2(10n2) = 1000f2(n2). Dla trzeciego algorytmu działaj ˛
a-cego w czasie wykładniczym mo˙zemy teraz oblicza´c tylko dane wej´sciowe o 10 dłu˙zsze, poniewa˙zf3(n3+ 10) = 1024f3(n3).
1.16
Zadania
1. Oblicz: a)P4 i=1i2i, b) P3 k=1k3, c) P4 n=1(n2−1), d) P3 i=1 P2 j=1ij2, e) P2 k=1 P4 n=1(k − n), 2. Oblicz: a)Q5 i=1(i + 1), b) Q4 k=1(2k + 1), c) Q4 n=1(n2− 1). 3. NiechA = {1, 2, 3, 4, 5}, B = {1, 3, 5, 7} i C = {4, 5, 6, 7, 8}. Oblicz A ∪ B ∪ C, A ∩ B ∩ C, A − B, A ∩ (B − C), A ⊕ B, A ⊕ B ⊕ C.4. Dane s ˛a dwa wielomianyU (x) = 4x3+ 3x + 2 oraz V (x) = 2x4+ x2+ 3x. Oblicz
ich sum˛e oraz iloczyn. Oblicz według schematu Horna warto´sciU (1) oraz V (1).
5. Podziel wielomianU (x) = 4x4+ 3x2+ x − 2 przez V (x) = x2+ x.
6. NiechI = {1, 2, 3, 4, 5} b¸edzie zbiorem indeksów. Dla ka˙zdego i ∈ I okre´slamy
zbórBi = {x ∈ N | i ≤ x ≤ 2i}. ObliczSi∈IBi,Ti∈IBi,A1⊕ A3⊕ A5oraz
1.16. Zadania 23
7. NiechI = {1, 2, 3, 4, 5} b¸edzie zbiorem indeksów. Dla ka˙zdego i ∈ I okre´slamy
zbórCi= {x ∈ N | 1 ≤ x ≤ 30 oraz i dzieli x}. ObliczSi∈ICiorazTi∈ICi.
8. NiechA = {1, 2, 3, 4}, B = {1, 2, 3}. Wypisz elementy A × B, B × A oraz {(a, b) ∈ A × B | a < b}.
9. NiechX = {a, b, c}. Wypisz elementy X2,X3oraz{(x, y) ∈ X2| x 6= y}.
10. Narysuj wszystkie grafy ze zbiorem wierzchołkówV = {a, b, c}. Które z nich s ˛a spójne?
11. Narysuj wszystkie drzewa ze zbiorem wierzchołkówV = {a, b, c}.
12. Narysuj wszystkie grafy skierowane ze zbiorem wierzchołkówV = {a, b}.
13. Narysuj grafG = (V, E), ze zbiorem wierzchołków V = {a, b, c, d, e} i zbiorem
kraw˛edziE = {{a, b}, {a, c}, {b, c}, {a, d}, {d, e}}. Czy graf G jest spójny? Czy
posiada cykle?
14. Narysuj graf skierowanyG = (V, E), ze zbiorem wierzchołków V = {a, b, c, d} i
zbiorem kraw˛edziE = {(a, b), (b, c), (c, b), (c, d), (d, d)}.
15. Wypisz 10 pierwszych słów zbioru{a, b, c}∗według porz ˛adku leksykograficznego
i kanonicznego.
16. Wypisz wszystkie prefiksy i sufiksy słowaaaba.
17. Uporz ˛adkuj nast˛epuj ˛acy zbiór słów według porz ˛adku leksykograficznego i kano-nicznego: słowik, wróbel, kos, jaskółka, kogut, dzi˛ecioł, gil, kukułka, szczygieł, sowa, kruk, czubatka, drozd, sikora i dzierlatka, kaczka, g ˛aska, jemiołuszka, dudek, trznadel, po´smieciuszka, wilga, zi˛eba, bocian, szpak. [Fragment wiersza Ptasie
ra-dio Juliana Tuwima]
18. Udowodnij wzóry (1.1), (1.2), (1.3), (1.4).
19. Udowodnij lemat 1.36,
20. Udowodnij zale˙zno´sci z przykładów 1.33, 1.34, 1.35.
21. Niechx, y b˛ed ˛a dowolnymi liczbami rzeczywistymi, ak dowoln ˛a liczb ˛a całkowit ˛a. Udowodnij nast˛epuj ˛ace zale˙zno´sci:
bx + yc ≥ bxc + byc. bx + kc = bxc + k. dx + ye ≤ dxe + dye. dx + ke = dxe + k.
23. Podaj przykład liczbx i y, dla których zachodzi dx + ye < dxe + dye.
24. Za pomoc ˛a algorytmu sortowania b ˛abelkowego posortuj ci ˛agi: a) 1,3,5,4,2; b) 8,1,6,3,4,5,2,7.