Obliczanie pól figur płaskich

(1)

Obliczanie pól figur płaskich

Autorzy:

Witold Majdak

(2)

Obliczanie pól figur płaskich

Autor: Witold Majdak

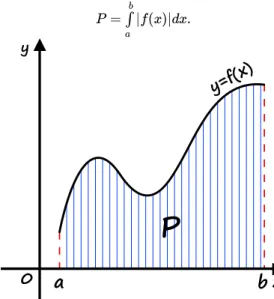
Z definicji całki oznaczonej Riemanna wynika, że jeżeli jest funkcją ciągłą i nieujemną w przedziale , to całka jest równa polu figury ograniczonej przez wykres funkcji , oś oraz proste i . Tak zadaną figurę, którą możemy opisać jako zbiór

nazywamy trapezem krzywoliniowymtrapezem krzywoliniowym. Jeżeli dla , to W rezultacie dla dowolnej funkcji ciągłej prawdziwy jest następujący związek:

Rysunek 1: Pole figury płaskiej zwanej trapezem krzywoliniowym

f : [a, b] → R

[a, b]

f(x)dx

∫

b a

P

f

OX

x = a x = b

{(x, y) ∈

R

2

: 0 ≤ y ≤ f(x), a ≤ x ≤ b},

f(x) ≤ 0

x ∈ [a, b]

P = −

∫

b

f(x)dx.

a

f : [a, b] → R

P = |f(x)|dx.

∫

a b P

(3)

PRZYKŁAD

Przykład 1:

Obliczmy pole obszaru zawartego pomiędzy wykresami funkcji , , gdzie oraz osią . Zauważmy, że rozpatrywana figura jest sumą dwóch trapezów krzywoliniowych i :

więc jej pole jest równe sumie pól tych trapezów. Korzystając z interpretacji geometrycznej całki oznaczonej, otrzymujemy

Szukane pole wynosi zatem

Rysunek 2: ,

PRZYKŁAD

Przykład 2:

Obliczmy pole obszaru ograniczonego przez elipsę o półosiach i ( ) daną równaniem

P

f(x) = x + 1

√

− −

−−−

g(x) = (x − 1)

2

_{x ∈ [−1, 1],}

OX

T

1

T

2

= {(x, y) ∈

: 0 ≤ y ≤

, x ∈ [−1, 0]},

= {(x, y) ∈

: 0 ≤ y ≤ (x − 1 , x ∈ [0, 1]},

T

1

R

2

√

− −

x + 1

−−−

T

2

R

2

)

2

P

T1

+

P

T2

P

T1

P

T2

=

∫

dx = (x + 1

= ,

−1 0

x + 1

− −

−−−

√

2 ₃

)

32

∣∣

0 −1

2

3 = (x − 1 dx = (x − 1

∫

= .

0 1

)

2

1

3 )

3

∣∣

1 0

1

3 P = + = 1.

2 3 13 = f(x)dx PT1 ∫ −1 0 = g(x)dx PT2 ∫ 0 1

a b a, b > 0

+

= 1.

x2 a2 y 2 b2

(4)

Rysunek 3: Obszar ograniczony przez elipsę

Na początku zauważmy, że rozważany obszar jest symetryczny względem osi układu współrzędnych, a więc możemy go podzielić na cztery obszary o identycznych polach. Pole części leżącej w pierwszej ćwiartce układu współrzędnych zawarte jest między osiami i oraz częścią krzywej zadanej przepisem

Jest to więc pole figury będącej trapezem krzywoliniowym. Wówczas gdzie

Obliczmy tę całkę poprzez zamianę zmiennych w całce oznaczonej. Niech więc

Zauważmy, że , czyli zawiera się w dziedzinie funkcji cyklometrycznej arcus sinus, a więc nowa zmienna jest poprawnie określona. Ponieważ funkcja arcus sinus jest funkcją rosnącą, to jeżeli zmienia się od do , to wartości rosną od do . Mamy więc

Tabela 1: Zmiana wartości granic całkowania, gdy {OPENAGHMATHJAX (type

Wówczas

a więc

Powołując się na twierdzenie o całkowaniu przez podstawienie, otrzymujemy

Ostatecznie pole figury ograniczonej przez elipsę o półosiach i wynosi .

+ = 1 x2 a2 y2 b2

OX OY

f(x) = b

1 −

x2

, gdzie x ∈ [0, a].

a2

− −

−−−

√

P = 4 ,

P

1

= f(x)dx = b

dx.

P

1

∫

0 a

∫

0 a

1 −

x2 a2

− −

−−−

√

t = arcsin

x

dla x ∈ [0, a].

a

∈ [0, 1]

x a xa

t

x

0 a

t

0

π 2

x 0 a

t 0

π 2

x = a sin t dla t ∈ [0, ],

π 2

dx = a cos t dt.

P = 4b

∫

a cos tdt = 4ab

tdt = 4ab

(1 + cos 2t)dt

0 π 2

1 −

sin

2

t

−

−−−−−

−

√

∫

0 π 2

cos

2

_∫

0 π 2

1

2 = 2ab(t +

sin 2t

₂

) = 2ab( +

∣∣

π2

− 0) = πab.

0

π

2 sin π

2

(5)

WNIOSEK

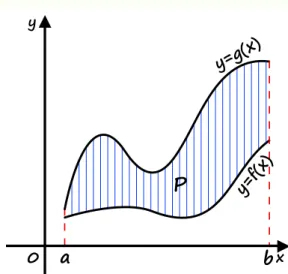
Wniosek 1: o polu figury ograniczonej przez wykresy dwóch funkcji oraz proste

pionowe

Jeżeli oraz są funkcjami ciągłymi, a ponadto dla każdego , to pole figury ograniczonej przez wykresy tych funkcji oraz proste i wyraża się wzorem

Rysunek 4: Pole figury ograniczonej przez wykresy funkcji i oraz proste i

f : [a, b] → R

g : [a, b] → R

f(x) ≤ g(x)

x ∈ [a, b]

P

x = a x = b

P = (g(x) − f(x))dx.

∫

a b

(6)

PRZYKŁAD

Przykład 3:

Znajdźmy pole figury zawartej między wykresami funkcji i oraz prostą

Rysunek 5: Pole figury zawartej między wykresami funkcji i oraz prostą

Dla każdego zachodzi nierówność więc szukane pole obliczamy w następujący sposób:

f(x) = e

−x

_{g(x) = e}

x

_{x = 1.}

P f g x = 1

x ∈ [0, 1]

f(x) ≤ g(x),

P = ( −

∫

) dx = ( +

) = e +

− 2.

0 1

e

x

_e

−x

_e

x

_e

−x

∣∣

1 0

e

−1

(7)

PRZYKŁAD

Przykład 4:

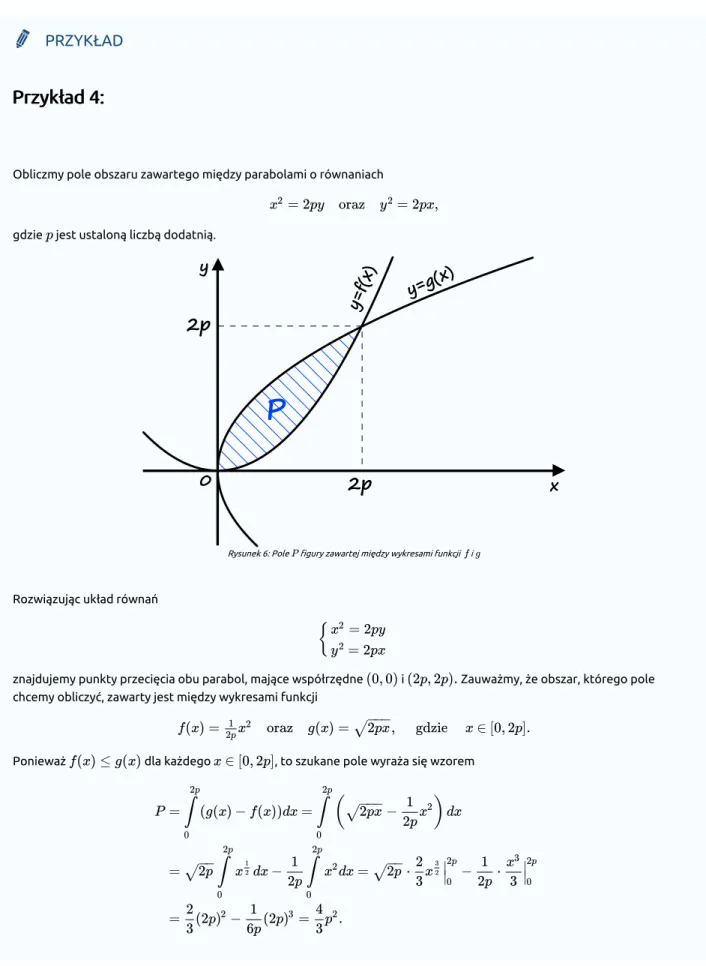
Obliczmy pole obszaru zawartego między parabolami o równaniach

gdzie jest ustaloną liczbą dodatnią.

Rysunek 6: Pole figury zawartej między wykresami funkcji i

Rozwiązując układ równań

znajdujemy punkty przecięcia obu parabol, mające współrzędne i Zauważmy, że obszar, którego pole chcemy obliczyć, zawarty jest między wykresami funkcji

Ponieważ dla każdego , to szukane pole wyraża się wzorem

Aby obliczyć pole figury płaskiej przy pomocy całki oznaczonej, w pewnych sytuacjach warto jest całkować względem zmiennej zamiast zmiennej . Pozwala to uniknąć dzielenia danego obszaru na mniejsze obszary oraz niepotrzebnego obliczania kilku całek.

= 2py oraz

= 2px,

x

2

_y

2

p

P f g

{ = 2py

x

2

= 2px

y

2

(0, 0) (2p, 2p).

f(x) =

1

oraz g(x) =

, gdzie x ∈ [0, 2p].

2p

x

2

√

2px

− −

−

f(x) ≤ g(x)

x ∈ [0, 2p]

P = (g(x) − f(x))dx =

∫

(

−

) dx

0 2p

∫

0 2p

2px

− −

−

√

_{2p x}

1

2

=

√ ∫

2p

−−

dx −

dx =

⋅

−

⋅

0 2p

x

12

1 2p ∫

0 2p

x

2

_√

−−

_2p

2 3 x

3 2

∣∣

2p 0

1 2p

x

3

3 ∣∣

2p 0

= (2p −

2 ₃

)

2

1 (2p =

.

6p

)

3

4 3 p

2

y

x

(8)

PRZYKŁAD

Przykład 5:

Pokażemy drugi sposób na znalezienie pola obszaru z przykładu 1. Zauważmy (rys. 2), że zadany obszar jest zbiorem

a jego pole obliczamy w następujący sposób:

Omówimy teraz sposób wyznaczania pola figury ograniczonej przez krzywą zadaną parametrycznie. Najpierw jednak podajmy definicję takiej krzywej.

DEFINICJA

Definicja 1: Krzywa zadana parametrycznie

Mówimy, że jest krzywą zadaną parametryczniekrzywą zadaną parametrycznie, jeżeli istnieją takie funkcje ciągłe oraz , że

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: o polu obszaru ograniczonego łukiem krzywej zadanej

o polu obszaru ograniczonego łukiem krzywej zadanej

parametrycznie

Niech będzie krzywą zadaną parametrycznie, jak jest to opisane w definicji Krzywa zadana parametrycznie. Załóżmy dodatkowo, że funkcja jest rosnąca i ma w każdym punkcie przedziału ciągłą pochodną, a funkcja jest nieujemna. Pole obszaru ograniczonego łukiem krzywej , odcinkiem osi OX oraz prostymi , , gdzie , , wyraża się wzorem

DOWÓD DOWÓD

W pierwszym kroku dowodu wykażemy, że przy przyjętych założeniach możemy wyrazić krzywą jako wykres funkcji ciągłej zmiennej na przedziale . Istotnie, ponieważ funkcja jest rosnąca w przedziale to

a ponadto funkcja ta jest odwracalna. To z kolei implikuje, że dla (gdzie oznacza funkcję odwrotną do ), co po podstawieniu do równania daje

Dalej, skoro funkcja jest nieujemna, to w konsekwencji funkcja zależna od zmiennej przyjmuje wartości nieujemne. Dzięki temu pole rozpatrywanego obszaru możemy obliczyć, stosując wzór

{(x, y) ∈

R

2

:

_y

2

− 1 ≤ x ≤ −

_√

_y

+ 1, y ∈ [0, 1]},

P = (−

∫

+ 1 − + 1) dy = ( −

−

+ 2y) = − − + 2 = 1.

0 1

y

√

y

2 2 3

y

3 2 1₃

y

3

∣∣

1 0 23 13

Γ

φ : [α, β] → R

ψ : [α, β] → R

Γ = {(x, y) ∈

R

2

: x = φ(t), y = ψ(t) dla t ∈ [α, β]}.

Γ

φ

[α, β]

ψ

P

Γ

x = a x = b

a = φ(α) b = φ(β)

P = ψ(t) (t)dt.

∫

α β

φ

′

Γ

x

[a, b]

φ

[α, β],

a = φ(α) ≤ φ(β) = b,

t =

φ

−1

(x)

_{x ∈ [a, b]}

_φ

−1

φ

y = ψ(t)

y = ψ(

φ

−1

(x)) dla x ∈ [a, b].

ψ

y

x

P = y(x)dx = ψ(

b b −1

(x))dx.

(9)

Aby obliczyć ostatnią całkę, zastosujmy twierdzenie o całkowaniu przez podstawienie dla , pamiętając przy tym o stosownej zmianie granic całkowania. Z równania , gdzie dostajemy . W rezultacie

CND. CND.

PRZYKŁAD

Przykład 6:

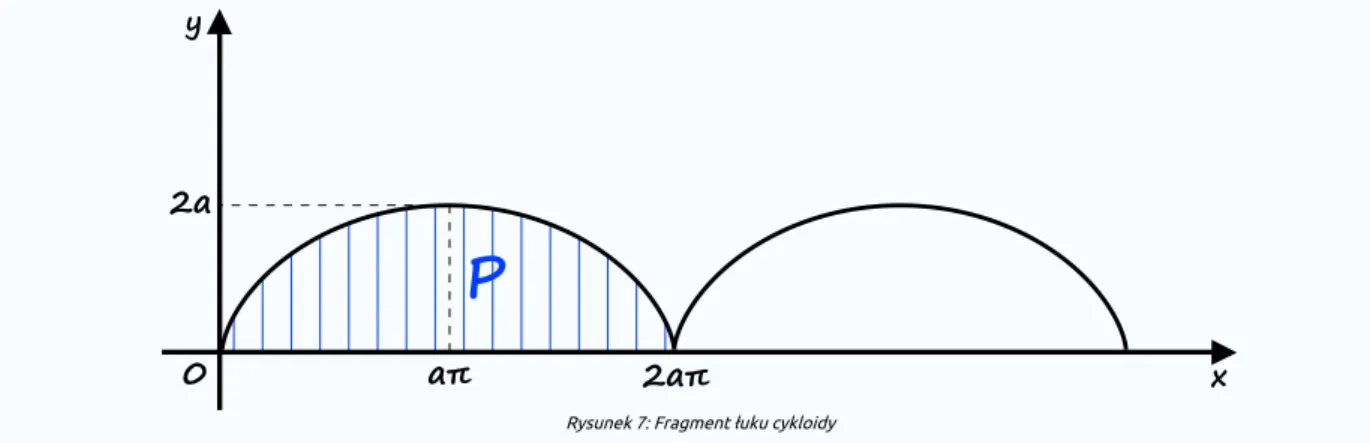
Obliczymy pole obszaru ograniczonego osią i jednym łukiem krzywej zwanej cykloidącykloidą , która zadana jest równaniami parametrycznymi

gdzie jest ustaloną liczbą dodatnią. Wyjaśnijmy, że cykloida to krzywa opisująca tor ruchu punktu leżącego na obwodzie koła o promieniu , które toczy się bez poślizgu po prostej. Zauważmy, że wartości powtarzają się cyklicznie, gdy parametr przebiega każdy z przedziałów gdzie jest liczbą całkowitą. Dla naszych potrzeb wybierzmy jeden z takich przedziałów, np.

Rysunek 7: Fragment łuku cykloidy

Zauważmy, że dla każdego więc spełnione są założenia twierdzenia o polu obszaru ograniczonego łukiem krzywej zadanej parametrycznie. Na jego podstawie otrzymujemy

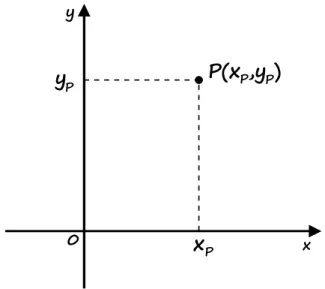
Jak wiadomo, położenie punktu na płaszczyźnie można określić dzięki wprowadzeniu na płaszczyźnie kartezjańskiegokartezjańskiego prostokątnego układu współrzędnych

prostokątnego układu współrzędnych. Wówczas położenie punktu jest jednoznacznie określone poprzez podanie pary , gdzie jest współrzędną tego punktu względem osi , zaś względem osi .

P = y(x)dx = ψ(

∫

(x))dx.

a b

∫

a b

φ

−1

t =

φ

−1

(x)

x = φ(t)

t ∈ [α, β],

dx = (t)dt

φ

′

P = ψ(t) (t)dt.

∫

α β

φ

′

OX

{ x = φ(t) := a(t − sin t),

y = ψ(t) := a(1 − cos t),

a

y = ψ(t)

t

[2kπ, 2(k + 1)π],

k

[0, 2π].

(t) = ψ(t) ≥ 0

φ

′

_{t ∈ [0, 2π],}

P =

∫

ψ(t) (t)dt =

a(1 − cos t) ⋅ a(1 − cos t)dt

0 2π

φ

′

∫

0 2π

=

a

2

_∫

(1 − cos t dt =

(1 − 2 cos t +

t)dt

0 2π

)

2

_a

2

_∫

0 2π

cos

2

=

a

2

⎛

(t − 2 sin t) +

(1 + cos 2t)dt

⎝

⎜

∣∣

2π₀

∫

0 2π

1

2 ⎞

⎠

⎟

= (2π + (t +

a

2

1 ) ) = (2π + π) = 3π .

2 sin 2t

2 ∣∣

2π 0

a

2

a

2

P

( , )

x

P

y

P

x

P

OX

y

P

OY

(10)

Rysunek 8: Położenie punktu na płaszczyźnie opisane w kartezjańskim prostokątnym układzie współrzędnych

Jednakże położenie punktu na płaszczyźnie można też określić w inny sposób - dzięki wprowadzeniu tzw. biegunowegobiegunowego (polarnego) układu współrzędnych

(polarnego) układu współrzędnych. Jest ono jednoznacznie określone poprzed podanie odległości od pewnego wyróżnionego na płaszczyźnie punktu zwanego biegunembiegunem oraz poprzez podanie kąta pomiędzy półprostą o początku w biegunie i przechodzącą przez punkt a inną wyróżnioną półosią o początku w biegunie, zwaną półosią biegunową. (Kąty skierowane przeciwnie do ruchu wskazówek zegara są dodatnie, a zgodnie z ruchem wskazówek zegara są ujemne).

Rysunek 9: Położenie punktu na płaszczyźnie opisane przy użyciu biegunowego układu współrzędnych

Jeżeli umieścimy biegun w punkcie , czyli w początku układu kartezjańskiego, zaś jako półoś biegunową przyjmiemy półoś dodatnią osi , to wówczas związki między obydwoma układami wyrażą się w następujący sposób:

Rysunek 10: Związek między opisem położenia punktu na płaszczyźnie w kartezjańskim prostokątnym układzie współrzędnych a w biegunowym układzie współrzędnych

P

φ

P

(0, 0)

OX

{

xr

= cos φ,

= sin φ.

y r

(11)

W rezultacie

PRZYKŁAD

Przykład 7:

Równanie półokręgu o środku w punkcie i promieniu ma postać , przy czym Ta sama krzywa we współrzędnych biegunowych ma równanie , przy czym

PRZYKŁAD

Przykład 8:

Krzywa zadana równaniem ze względu na związki ma we współrzędnych biegunowych równanie

czyli

Omówimy teraz, w jaki sposób można obliczyć pole figury ograniczonej, której fragment brzegu jest zadany za pomocą współrzędnych biegunowych.

DEFINICJA

Definicja 2: Krzywa zadana biegunowo

Mówimy, że jest krzywą zadaną biegunowokrzywą zadaną biegunowo , jeżeli istnieje nieujemna funkcja ciągła taka, że

Zauważmy, że krzywą zadaną biegunowo można przedstawić w następujący sposób w postaci parametrycznej (w zależności od parametru ):

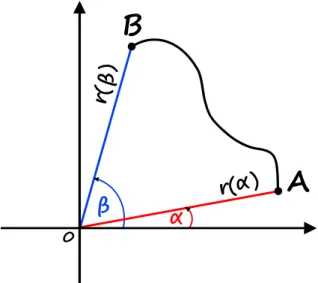
Niech oraz załóżmy, że Wtedy promienie wodzące o amplitudach i , czyli odcinki i , oraz łuk krzywej wyznaczają obszar zilustowany na poniższym rysunku.

{ x = r cos φ,

y = r sin φ.

(0, 0)

4 x

2

+ = 4

_y

2

_{y ≥ 0.}

r = 2

φ ∈ [0, π].

( +

x

2

_y

2

₎

2

= 2xy

_{x = r cos φ, y = r sin φ}

= 2 sin φ cos φ,

r

4

_r

2

= sin 2φ.

r

2

Γ

r : [α, β] → R

Γ = {(r, ϕ) ∈

R

2

: r = r(ϕ), ϕ ∈ [α, β]}.

ϕ

x = r(ϕ) cos ϕ oraz y = r(ϕ) sin ϕ, gdzie ϕ ∈ [α, β].

O = (0, 0), A = (r(α), α), B = (r(β), β)

0 < β − α < 2π.

(12)

Rysunek 11: Trapez krzywoliniowy w sensie biegunowego układu współrzędnych

Taki obszar nazywamy trapezem krzywoliniowym w sensie biegunowego układu współrzędnych. Jego pole możemy obliczyć korzystając z następującego twierdzenia.

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: o polu obszaru ograniczonego łukiem krzywej zadanej biegunowo

o polu obszaru ograniczonego łukiem krzywej zadanej biegunowo

oraz dwoma promieniami wodzącymi

Niech będzie krzywą zadaną biegunowo. Pole obszaru ograniczonego łukiem krzywej oraz promieniami wodzącymi o amplitudach i wyraża się wzorem

DOWÓD DOWÓD

Dla każdego podzielmy przedział na podprzedziałów tak dobierając punkty aby zachodziła zależność

W ten sposób otrzymujemy trójkątów krzywoliniowych zawartych między łukiem krzywej oraz promieniami wodzącymi o amplitudach i Oznaczmy przez długość odcinka tzn.

gdzie Niech będzie największą ze średnic wszystkich przedziałów czyli

Następnie dla każdego wybierzmy kąt pośredni Przy małych wartościach pole -tego trójkąta jest w przybliżeniu równe polu wycinka kołowego o promieniu i kącie środkowym wyrażającego się wzorem

gdzie jest miarą łukową tego kąta środkowego. Oznaczmy przez sumę pól wszystkich tych wycinków. Wówczas

Przechodząc do granicy (jak w konstrukcji całki oznaczonej Riemanna), otrzymujemy

Γ

P

Γ

α β

P =

1

(ϕ)dϕ.

2

∫

α β

r

2

n ∈ N

[α, β] n

[

ϕ

k−1

, ]

ϕ

k

(k = 1, …, n)

ϕ

k

,

α =

ϕ

0

<

ϕ

1

<

ϕ

2

< … <

ϕ

n

= β.

n

Γ

ϕ

k−1

ϕ

k

.

Δϕ

k

[

ϕ

k−1

, ],

ϕ

k

Δ =

ϕ

k

ϕ

k

−

ϕ

k−1

,

k ∈ {1, …, n}.

δ

n

[

ϕ

k−1

, ],

ϕ

k

= max{Δ : k = 1, …, n}.

δ

n

ϕ

k

k ∈ {1, …, n}

ξ

k

∈ [

ϕ

k−1

, ].

ϕ

k

Δϕ

k

P

k

r( )

ξ

k

Δ ,

ϕ

k

=

( )Δ ,

P

k 1₂

r

2

ξ

k

ϕ

k

Δϕ

k

P

n

=

( )Δ .

P

n

∑

k=1 n

P

k

∑

k=1 n ₁ 2

r

2

ξ

k

ϕ

k

P =

n

=

2

( )Δ =

k k

(ϕ)dϕ.

β 2

(13)

CND. CND.

Zastosujmy powyższy wzór do obliczenia pola figury ograniczonej przez krzywą zadaną biegunowo.

PRZYKŁAD

Przykład 9:

Wyznaczmy pole figury ograniczonej przez kardioidękardioidę, czyli krzywą zdefiniowaną biegunowo za pomocą przepisu

przy czym jest ustaloną liczbą dodatnią. Aby narysować tę krzywą, skorzystajmy ze znajomości wykresu funkcji cosinus. Otóż, gdy wartości kąta rosną od do , to wartości cosinusa maleją od do , a więc promień maleje od

do . Z kolei, gdy rośnie od do , to wartości funkcji cosinus maleją od do , a więc promień maleje od do . Ponadto promień rośnie od do dla kąta zmieniającego się od do . Ponieważ wykres funkcji cosinus jest symetryczny względem osi , to kardioida jest symetryczna względem osi .

Rysunek 12: Kardioida

Korzystając z twierdzenia o polu obszaru ograniczonego łukiem krzywej zadanej biegunowo oraz dwoma promieniami wodzącymi i symetrii rozpatrywanego obszaru względem osi , otrzymujemy

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

P =

_n→∞

lim

P

n

=

_n→∞

lim

∑

( )Δ =

(ϕ)dϕ.

k=1 n 1 2

r

2

ξ

k

ϕ

k 1₂

∫

α β

r

2

r = a(1 + cos ϕ), gdzie ϕ ∈ [−π, π],

a

ϕ

0

π

2

0 −1

r

a(1 + cos 0) = 2a

a(1 + cos ) = a

π

2

ϕ

π2

π

1 −1

r

a

a(1 + cos π) = 0

r

0 2a

ϕ

−π

0 OY

OX

P = 2 ⋅

1 _{2 ∫}

(ϕ)dϕ =

(1 + cos ϕ dϕ =

(1 + 2 cos ϕ +

ϕ)dϕ

α β

r

2

_∫

0 π

a

2

₎

2

_a

2

_∫

0 π

cos

2

= [ϕ + 2 sin ϕ +

a

2

∣∣

π

(1 + cos 2ϕ)dϕ ] = [π + ϕ + ⋅

]

0

∣∣

π 0

∫

0 π

1

2 a

2

1

2 ∣∣

π 0

1

2 sin 2ϕ

2 ∣∣

π 0

= 2 [π + ] = 3π .

a

2

π

2 a

2

(14)

Data generacji dokumentu: 2019-04-16 01:27:06

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=8f4c3d2979454d36dce38ea5accc4d0c