Badanie przebiegu
zmienności funkcji
Autorzy:
Ilona Michalik
Badanie przebiegu zmienności funkcji
Badanie przebiegu zmienności funkcji
Autor: Ilona Michalik
Fundamentalne dla rachunku różniczkowego pojęcia, takie jak granica, ciągłość, pochodna, są niezwykle skutecznymi narzędziami do badania przebiegu zmienności funkcji. Przez badanie przebiegu zmienności funkcji rozumiemy wykrywanie zasadniczych cech jej wykresu, gdy znamy funkcję jedynie jako abstrakcyjny przepis. Dzięki granicom obliczamy jej asymptoty, pochodna wykrywa jej monotoniczność i ekstrema, zaś badanie drugiej pochodnej umożliwia nam znalezienie punktów przegięcia i określenie
przedziałów wypukłości funkcji. Badanie przebiegu zmienności stanowi zatem syntezę i ukoronowanie całości metod rachunku różniczkowego i, jako takie, jest zarazem dużym wyzwaniem rachunkowym ze względu na swoją złożoność. W celu ułatwienia tego zadania organizuje się pracę według następujących kroków, zwanych schematem badania funkcji.
Aby zbadać przebieg zmienności funkcji, należy: 1. wyznaczyć dziedzinę funkcji,
2. zbadać parzystość, nieparzystość i okresowość (tylko wtedy, gdy podejrzewamy, że taka własność zachodzi), 3. wyznaczyć miejsca zerowe funkcji oraz punkty przecięcia z osią ,
4. wyznaczyć granice lub wartości na końcach przedziałów określoności funkcji, 5. wyznaczyć asymptoty pionowe i ukośne,
6. wyznaczyć przedziały monotoniczności i ekstrema lokalne, 7. wyznaczyć przedziały wypukłości i punkty przegięcia, 8. narysować wykres funkcji.
PRZYKŁAD
Przykład 1:
Przykład 1:
Zbadajmy przebieg zmienności funkcji .
Wyznaczamy dziedzinę funkcji.
Sprawdzamy parzystość i nieparzystość funkcji. Dziedzina jest zbiorem symetrycznym względem punktu zerowego osi .
Wynika stąd, że funkcja jest nieparzysta. Zatem wykres funkcji jest symetryczny względem punktu . Wyznaczamy miejsca zerowe funkcji.
Punktem przecięcia z osią jest , ponieważ . Wyznaczamy granice na końcach przedziałów dziedziny.
Na podstawie dziedziny funkcji i powyższych granic możemy stwierdzić, że proste oraz są asymptotami pionowymi obustronnymi funkcji .
Oy
f(x) =
x
− 1
x
2= (−∞, −1) ∪ (−1, 1) ∪ (1, +∞).
D
fOx
f(−x) =
−x
− 1
≠ f(x),
x
2f(−x) =
x
2−x
− 1
= −f(x).
(0, 0)
f(x) = 0 ⇔ (
x= 0 ∧ x ∈
) ⇔ (x = 0 ∧ x ∈
) ⇔ (x = 0).
−1 x2D
fD
fOy
x = 0
f(0) = 0
= [
] = [−1 ⋅
] = [−1 ⋅ ∞] = −∞,
lim
x→−1−x
− 1
x
2−1
0
+0
1
+= [
] = [−1 ⋅
] = [−1 ⋅ (−∞)] = +∞,
lim
x→−1+x
− 1
x
2−1
0
−0
1
−= [
] = −∞,
lim
x→1−x
− 1
x
20
1
−= [
] = +∞.
lim
x→1+x
− 1
x
20
1
+x = −1
x = 1
f
=
1= [ ] = 0.
Wynika stąd, że prosta jest asymptotą poziomą funkcji zarówno przy oraz przy . Nie zawsze jednak tak bywa, że ta sama prosta jest asymptotą i w , i w . W tym przypadku nie musimy już wyznaczać asymptot ukośnych, ponieważ asymptoty pionowe są ich szczególnym przypadkiem, a w może istnieć maksymalnie jedna asymptota ukośna i w może istnieć maksymalnie jedna asymptota ukośna.
Wyznaczamy pierwszą pochodną funkcji, a za jej pomocą przedziały monotoniczności oraz ekstrema (o ile istnieją).
Dziedzina pochodnej funkcji jest równa dziedzinie funkcji . Szukamy punktów, w których zeruje się pierwsza pochodna.
zatem funkcja nie posiada ekstremów.
Pochodna funkcji jest ujemna w przedziałach , oraz , więc funkcja jest tam przedziałami malejąca (nie musi być malejąca w sumie tych przedziałów).
Wyznaczamy przedziały wypukłości.
Dziedzina drugiej pochodnej funkcji jest równa dziedzinie funkcji .
Funkcja jest wypukła w przedziałach oraz , a wklęsła w przedziałach oraz . Funkcja ma punkt przegięcia w .
Poniższa tabelka może być pomocna przy rysowaniu wykresu funkcji :
x
'
(x)
''
(x)
f(x)
-1
(-1,0)
0
(0,1)
1
-
-
-
-
-0
+
-
+
f
f
-0
o
-+o
p.p.o
-+o
Rysunek 1: Tabelka przebiegu zmienności funkcji .
=
= [ ] = 0.
lim
x→−∞x
− 1
x
2 x→−∞lim
1 x1 −
1 x20
1
=
= [ ] = 0.
lim
x→+∞x
− 1
x
2 x→+∞lim
1 x1 −
1 x20
1
y = 0
f
x → +∞
x → −∞
+∞
−∞
−∞
+∞
(x) =
=
.
f
′x
′( − 1) − x( − 1
x
2x
2)
′( − 1
x
2)
2− − 1
x
2( − 1
x
2)
2f
f
(x) = 0 ⇔ (
= 0 ∧ x ∈
) ⇔ − − 1 = 0 ∧ x ∈
⇔ x ∈ ∅,
f
′− − 1
x
2( − 1
x
2)
2D
f′x
2D
f′(x) > 0
f
′(x) < 0
f
′⇔ (
( − 1
− − 1
x
2> 0 ∧ x ∈
) ⇔ − − 1 > 0 ∧ x ∈
⇔ x ∈ ∅.
x
2)
2D
f′x
2D
f′⇔ (
( − 1
− − 1
x
2< 0 ∧ x ∈
) ⇔ − − 1 < 0 ∧ x ∈
x
2)
2D
f′x
2D
f′⇔ x ∈ (−∞, −1) ∪ (−1, 1) ∪ (1, +∞).
(−∞, −1) (−1, 1)
(1, +∞)
f
(x) =
=
.
f
′′(− − 1 ( − 1 − (− − 1)[( − 1
x
2)
′x
2)
2x
2x
2)
2]
′( − 1
x
2)
42 + 6x
x
3( − 1
x
2)
3f
f
(x) = 0
f
′′(x) > 0
f
′′(x) < 0
f
′′⇔ (
( − 1
2 + 6x
x
3= 0 ∧ x ∈
) ⇔ (2 + 6x = 0 ∧ x ∈
)
x
2)
3D
f′′x
3D
f′′⇔ (2x( + 3) = 0 ∧ x ∈
x
2D
f′′) ⇔ x = 0,
⇔ (
( − 1
2 + 6x
x
3> 0 ∧ x ∈
) ⇔ (2x( + 3)( − 1 > 0 ∧ x ∈
)
x
2)
3D
f′′x
2x
2)
3D
f′′⇔ (x ∈ (−1, 0) ∨ x ∈ (1, ∞)) ,
⇔ (
( − 1
2 + 6x
x
3< 0 ∧ x ∈
) ⇔ (2x( + 3)( − 1 < 0 ∧ x ∈
)
x
2)
3D
f′′x
2x
2)
3D
f′′⇔ (x ∈ (−∞, −1) ∨ x ∈ (0, 1)) .
f
(−1, 0)
(1, ∞)
(−∞, −1)
(0, 1)
f
x = 0
f
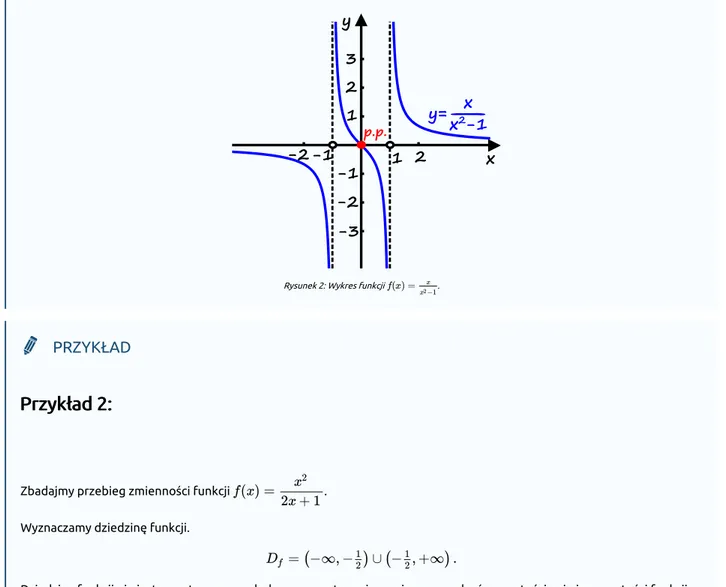
f(x) = x −1 x2Wykres funkcji przedstawia następujący rysunek:
Rysunek 2: Wykres funkcji .
PRZYKŁAD
Przykład 2:
Przykład 2:
Zbadajmy przebieg zmienności funkcji .
Wyznaczamy dziedzinę funkcji.
Dziedzina funkcji nie jest symetryczna względem zera, zatem nie musimy sprawdzać parzystości ani nieparzystości funkcji. Funkcja nie jest ani parzysta ani nieparzysta.
Wyznaczamy miejsca zerowe funkcji.
Punktem przecięcia z osią jest , ponieważ . Wyznaczamy granice na końcach przedziałów określoności.
Wynika stąd, że prosta jest asymptotą pionową obustronną funkcji .
Funkcja nie ma asymptot poziomych. Sprawdzamy czy istnieją asymptoty ukośne.
f
f(x) = x −1 x2f(x) = x
2x + 1
2= (−∞, − ) ∪ (− , +∞) .
D
f 12 12f(x) = 0 ⇔ (
x2= 0 ∧ x ∈
) ⇔ (x = 0 ∧ x ∈
) ⇔ x = 0.
2x+1D
fD
fOy
x = 0
f(0) = 0
= [
] = [ ⋅
] = [ ⋅ (−∞)] = −∞,
lim
x→−1 2 −x
22x + 1
1 40
−1
4
0
1
−1
4
= [
] = [ ⋅
] = [ ⋅ ∞] = +∞.
lim
x→−1 2 +x
22x + 1
1 40
+1
4
0
1
+1
4
x = −
12f
=
= [
] = −∞,
lim
x→−∞x
22x + 1
x→−∞lim
x
2 +
1 x−∞
2
=
= [
] = +∞,
lim
x→+∞x
22x + 1
x→+∞lim
x
2 +
1 x+∞
2
=
=
= = ,
lim
x→−∞f(x)
x
x→−∞lim
x
22 + x
x
2 x→−∞lim
1
2 +
1 x1
2
a
1(f(x) − x) =
(
− x) =
=
= − = ,
lim
x→−∞a
1 x→−∞lim
x
22x + 1
1
2
x→−∞lim
−x
4x + 2
x→−∞lim
−1
4 +
2 x1
4
b
1=
=
= = ,
f(x)
2 2Z powyższych równości wynika, że prosta jest asymptotą ukośną funkcji przy oraz przy . Wyznaczamy pierwszą pochodną funkcji, a za jej pomocą przedziały monotoniczności oraz ekstrema (o ile istnieją).
Dziedzina pochodnej funkcji jest równa dziedzinie funkcji . Szukamy punktów, w których zeruje się pierwsza pochodna.
W punktach lub funkcja może posiadać ekstremum. Sprawdzamy czy punkty te spełniają warunek wystarczający istnienia ekstremum.
Funkcja jest malejąca w przedziałach oraz , rosnąca w przedziałach oraz . W punkcie funkcja ma maksimum, natomiast w punkcie minimum.
Wyznaczamy przedziały wypukłości.
Dziedzina drugiej pochodnej funkcji jest równa dziedzinie funkcji
Funkcja jest wypukła w przedziale , a wklęsła w przedziale . Funkcja nie ma punktów przegięcia.
Sporządzamy tabelkę przebiegu zmienności funkcji .
x
'
(x)
''
(x)
f(x)
-
-+
-
+
f
f
-1 2 -
-
-12-
1 2-1
1
0
0
+
0
0
+
-
+
- 1
0
-1 -1 +o
o
+ max. min.Rysunek 3: Tabelka przebiegu zmienności funkcji .
=
=
= = ,
lim
x→+∞f(x)
x
x→+∞lim
x
22 + x
x
2 x→+∞lim
1
2 +
1 x1
2
a
2(f(x) − x) =
(
− x) =
=
= − = .
lim
x→+∞a
2 x→+∞lim
x
22x + 1
1
2
x→+∞lim
−x
4x + 2
x→+∞lim
−1
4 +
2 x1
4
b
2y = x −
12 14f
x → +∞
x → −∞
(x) =
=
=
.
f
′(
x
2)
′(2x + 1) − (2x + 1
(2x + 1)
x
22)
′2x(2x + 1) − 2x
(2x + 1)
2 2(2x + 1)
2 + 2x
x
2 2f
f
(x) = 0
f
′⇔ (
2 + 2x
x
2= 0 ∧ x ∈
) ⇔ (2x(x + 1) = 0 ∧ x ∈
)
(2x + 1)
2D
f′D
f′⇔ (x = 0 ∨ x = −1) .
x = −1
x = 0
(x) > 0
f
′(x) < 0
f
′⇔ (
(2x + 1)
2 + 2x
x
2 2> 0 ∧ x ∈
D
f′) ⇔ (2x(x + 1)(2x + 1 > 0 ∧ x ∈
)
2D
f′)
⇔ x ∈ (−∞, −1) ∪ (0, ∞),
⇔ (
(2x + 1)
2 + 2x
x
2 2< 0 ∧ x ∈
D
f′) ⇔ (2x(x + 1)(2x + 1 < 0 ∧ x ∈
)
2D
f′)
⇔ x ∈ (−1, − ) ∪ (− , 0) .
1
2
1
2
f
(−1, − )
1 2(− , 0)
12(−∞, −1)
(0, ∞)
x = −1
x = 0
(x)
f
′′= (2 + 2x (2x + 1 − (2 + 2x)[(2x + 1
x
2)
′)
2x
2)
2]
′(2x + 1)
4=
(4x + 2)(2x + 1 − 4(2 + 2x)(2x + 1)
)
(2x + 1)
2x
42=
(2x + 1)
2
3.
f
f
(x) = 0 ⇔ (
= 0 ∧ x ∈
) ⇔ x ∈ ∅,
f
′′2
(2x + 1)
3D
f′′(x) > 0 ⇔ (
> 0 ∧ x ∈
) ⇔ x > − ,
f
′′2
(2x + 1)
3D
f′′1
2
(x) < 0 ⇔ (
< 0 ∧ x ∈
) ⇔ x < − .
f
′′(2x + 1)
2
3D
f′′1
2
f
(−∞, − )
1 2(− , +∞)
12f
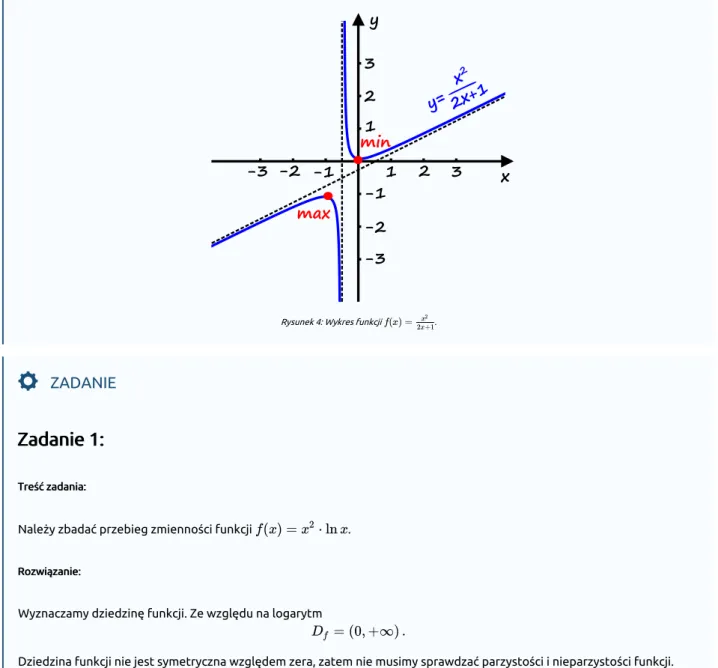
f(x) = x2 2x+1Wykres funkcji przedstawia następujący rysunek:
Rysunek 4: Wykres funkcji .
ZADANIE
Zadanie 1:
Zadanie 1:
Treść zadania: Treść zadania:
Należy zbadać przebieg zmienności funkcji .
Rozwiązanie: Rozwiązanie:
Wyznaczamy dziedzinę funkcji. Ze względu na logarytm
Dziedzina funkcji nie jest symetryczna względem zera, zatem nie musimy sprawdzać parzystości i nieparzystości funkcji. Funkcja nie jest parzysta ani nieparzysta.
Wyznaczamy miejsca zerowe funkcji.
Wykres funkcji nie przecina osi , ponieważ nie należy do dziedziny funkcji. Wyznaczamy granice na końcach przedziałów określoności oraz asymptoty.
Wynika stąd, że funkcja nie ma asymptot pionowych.
Funkcja nie ma asymptot poziomych. Sprawdzamy czy istnieją asymptoty ukośne.
zatem funkcja nie ma także asymptot ukośnych, gdyż wynik tej granicy nie jest liczbą skończoną.
Wyznaczamy pierwszą pochodną funkcji, a za jej pomocą przedziały monotoniczności oraz ekstrema (o ile istnieją).
f
f(x) = x2 2x+1f(x) =
x
2⋅ ln x
= (0, +∞) .
D
ff(x) = 0 ⇔ ( ⋅ ln x = 0 ∧ x ∈
x
2D
f) ⇔ [(x = 0 ∨ x = 1) ∧ x ∈
D
f] ⇔ x = 1.
Oy
x = 0
⋅ ln x
=
= 0.
lim
x→0+x
2=
[0⋅∞]lim
x→0+ln x
1 x2=
[ ]∞ ∞ Hlim
x→0+ 1 x −2 x3lim
x→0+x
2−2
⋅ ln x = +∞.
lim
x→+∞x
2=
x ⋅ ln x = +∞,
lim
x→+∞f(x)
x
x→+∞lim
(x) = (
⋅ ln x + ⋅ (ln x = 2x ⋅ ln x + ⋅ = x(2 ln x + 1).
f
′x
2)
′x
2)
′x
2 1 xDziedzina pochodnej funkcji jest równa dziedzinie funkcji . Szukamy punktów, w których zeruje się pierwsza pochodna.
W punkcie funkcja może mieć ekstremum. Sprawdzamy czy punkt ten spełnia warunek wystarczający istnienia ekstremum.
Funkcja jest malejąca w przedziale , rosnąca w przedziale . W punkcie funkcja osiąga minimum.
Wyznaczamy przedziały wypukłości.
Dziedzina drugiej pochodnej funkcji jest równa dziedzinie funkcji .
Funkcja jest wypukła w przedziale , a wklęsła w przedziale . Funkcja ma punkt przegięcia w .
Sporządzamy tabelkę przebiegu zmienności funkcji .
x
'
(x)
''
(x)
f(x)
-
-+
-
+
f
f
+
0
+
0
(
0
e
--32)
e
--32(
e
--32e
--21)
e
--12(
e
--211
)
1
1
o
-3 -2e3 -3 -2e3 -1 2e - --12eo
0
+
+
-+
+
-3 -2e3 --12eo
+ p.p. min.Rysunek 5: Tabelka przebiegu zmienności funkcji .
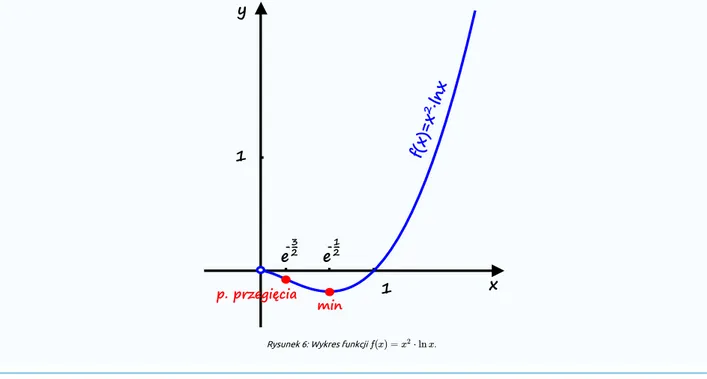
Wykres funkcji przedstawia następujący rysunek:
f
f
(x) = 0
f
′⇔ (x(2 ln x + 1) = 0 ∧ x ∈
D
f′)
⇔ [(x = 0 ∨ x =
e
−1) ∧ x ∈
]
2D
f′⇔ x =
e
−1.
2x = e
−1 2(x) > 0 ⇔ (x(2 ln x + 1) > 0 ∧ x ∈
) ⇔ x ∈ (
, +∞) ,
f
′D
f′e
−12(x) < 0 ⇔ (x(2 ln x + 1) < 0 ∧ x ∈
) ⇔ x ∈ (0,
) .
f
′D
f′e
−12f
(0,
e
−1)
2(
e
−12, +∞)
x = e
−12(x) = ⋅ (2 ln x + 1) + x(2 ln x + 1 = 2 ln x + 1 + x = 2 ln x + 3.
f
′′x
′)
′ 2 xf
f
(x) = 0 ⇔ (2 ln x + 3 = 0 ∧ x ∈
) ⇔ x =
,
f
′′D
f′′e
−32(x) > 0 ⇔ (2 ln x + 3 > 0 ∧ x ∈
) ⇔ x ∈ (
, +∞) ,
f
′′D
f′′e
−32(x) < 0 ⇔ (2 ln x + 3 < 0 ∧ x ∈
) ⇔ x ∈ (0,
) ,
f
′′D
f′′e
−32f
(
e
−3, +∞)
2(0,
e
−32)
x = e
−3 2f
f(x) =x2⋅ ln xf(x)
Rysunek 6: Wykres funkcji .
Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie
http://creativecommons.org/licenses/by-sa/3.0/pl/.
Data generacji dokumentu: 2019-04-15 10:08:59
Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=d7f310feeb22cedc49c8187f50e4148c
Autor: Ilona Michalik