Metaheurystyki w Rn Ewolucja różnicowa, EDA, CMAES, Rój cząstek

(1)

ALHE Jarosław Arabas Metaheurystyki w Rn Ewolucja różnicowa EDA CMAES Rój cząstek

(2)

Metoda przeszukiwania I : S×U∗ → X ∗ selekcja S1 S2 S3 S4 S5 S6 S7 S8 S9 S10S11S12 S0 wariacja S4 S8 S2 o_s: Π×H ×U ∗ → X∗ o_m: Π× X∗×M → M o_v: M ×U ∗×X∗ → X∗ adaptacja stan inicjacja S1 S0

(3)

Typowe sposoby generacji sąsiadów ● Rozkład jednostajny w kostce ● Rozkład jednostajny w podprzestrzeni ● Rozkład normalny

(4)

Typowe sposoby

generacji punktów “pomiędzy”

● Rozkład jednostajny w kostce ● Rozkład jednostajny na odcinku łaczącym ● Rozkład jednostajny na zbiorze narożników kostki

(5)

Rozkład próbkowania

● Sposób tworzenia nowych punktów można

opisać za pomocą zmiennej losowej, której rozkład da się analizować

● Jest to rozkład próbkowania

● Rozkład próbkowania może być założony z

góry lub może się adaptować

(6)

Optymalizacja jako proces adaptacji

● Przekonanie o położeniu optimum

?

x q(x)

(7)

x q(x)

(8)

x q(x)

(9)

x q(x)

(10)

x q(x)

(11)

x q(x)

(12)

x q(x)

(13)

● Obserwujemy wartości funkcji celu w wielu

punktach

● Okolice każdego punktu są tym chetniej

(14)

● Obserwujemy

wartości funkcji celu w wielu punktach

● Okolice każdego

punktu są tym

chetniej próbkowane, im jest on lepszy

(15)

(16)

Mieszanina rozkładów p-stwa

x q(x)

(17)

x q(x)

(18)

x q(x)

(19)

Ewolucja różnicowa

algorytm differential evolution inicjuj P0 ← {P_1,0 P₂0... P_μ0} H ← P0 t ← 0 while ! stop for (i∈1 :μ) Pt_j ← select (Pt) P_kt , P_lt ← sample (Pt) M_it ← Pt_j+ F (P_kt−P_lt) O_it ← crossover (P_it , M_it) H ← H ∪{O_it } P_it+ 1 ←tournament ( P_it ,O_it) t ← t+ 1

sample jest procesem wyboru

pary punktów z jednakowym p-stwem crossover jest operacją krzyżowania wymieniającego

(20)

Typy ewolucji różnicowej - klasyka

● Typ selekcji

● wybór losowego (rand)

● wybór najlepszego w populacji (best)

● Typ krzyżowania

● dwumianowe (bin) ● wykładnicze (exp)

● Liczba par różnicowanych punktów – 1 albo 2 ● Konwencja oznaczeń: DE/rand/1/bin

(21)

Typy krzyżowania

procedure binomial crossover arguments : x , y for (i∈1: n) if a< c_r z_i ← y_i else z_i ← x_i return z

procedure exponential crossover arguments : x , y i ← 1 while (i≤n) if a< c_r z_i ← y_i else break while (i≤n) z_i ← x_i return z

a jest zmienną losową o rozkładzie jednostajnym w (0,1)

(22)

Krzyżowanie wykładnicze a jednopunktowe 0.062 -1.893 0.053 0.0759 0.631 -0.299 0.194 0.328 0.631 -0.299 0.053 0.328 1 1 0 1 Rodzic 1 Rodzic 2 Potomek wagi

(23)

Krzyżowanie wykładnicze a jednopunktowe

1 1 0

1

W krzyżowaniu jednopunktowym rozkład prawdopodobieństwa pojawienia się przejścia między jedynką a zerem jest rozkładem jednostajnym

W krzyżowaniu wykładniczym rozkład ten jest rozkładem (prawie) wykładniczym wagi 1/5 1 1 0 1 1/5 1/5 1/5 1/5 1/2 1 1 0 1 1/4 1/8 1/16 1/16 p p2 _p3 _p4 _{dopełnienie do 1}

(24)

Krzyżowanie równomierne a dwumianowe 0.062 -1.893 0.053 0.0759 0.631 -0.299 0.194 0.328 0.631 -0.299 0.053 0.0759 1 1 0 0 Rodzic 1 Rodzic 2 Potomek wagi

(25)

Krzyżowanie równomierne a dwumianowe

1 1 0

0

W krzyżowaniu równomiernym prawdopodobieństwo pojawienia się jedynki i zera na każdej pozycjii jest równe 1/2

W krzyżowaniu dwumianowym te p-stwa są różne

W obu przypadkach, rozkład p-stwa pojawienia się k jedynek i n-k zer jest rozkładem Bernoulliego (wg angielskiej nomenklatury dwumianowym)

wagi 1/2 1 1 0 0 1 1 0 0 1-p_e 1/2 1/2 1/2 p_e p_e 1-p_e

(26)

DE/rand/1

S1 S2 S3 S4 S5 S6 S7 S8 S9 S0

Strzałki między punktami Sx oraz Sy oznaczają, że punkt Sy jest lokalną modyfikacją punktu Sx

S11S12S13 S14 S15 S16 S17 S18 S19

S10 S20

P0 O0 O1 O2 O3

Trzy punkty wpływają na jeden Trzy punkty wpływają na jeden

Najlepszy punkt pierwszej pozycji populacji Najlepszy punkt drugiej pozycji populacji Najlepszy punkt trzeciej pozycji populacji

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

● Inne metody selekcji

● current-to-best ● current-to-rand ● rand-to-best ● Krzyżowanie uśredniające ● DE/either-or KP_it+ (1−K ) Pt_best KP_it+ (1−K ) Pt_j KP_bestt + (1−K ) Pt_j z=

{

Pi t + F (Pt_j−P_kt ) KPt+ (1−K )( Pt+ Pt ) z p−stwem p_F z p−stwem 1− p

}

z=KP_it+ (1−K ) v

(35)

● Poinformowanie T ● Determinizm N

● Typ stanu pamięciowy

● Wielkość modelu liczność populacji ● Lokalność generacji T

● Miękkość selekcji N

● Okno historii nieskończone

(36)

Algorytm ewolucyjny wypukła funkcja celu

● Model populacji nieskończonej

● Dystrybuanta empiryczna punktów populacji

(skokowa) → dystrybuanta rozkładu próbkowania (ciągła)

(37)

DE/rand/1

wypukła funkcja celu

● Wariancja punktów po selekcji ● Wariancja punktów po mutacji

● Krzyżowanie zmienia wariancję (wzór dla bin) ●

v_P

v_O=v_P+ F2(v_P+ v_P)=v_P(1+ 2F2)

(38)

DE/rand/1

wypukła funkcja celu -wariancja po sukcesji

(39)

DE/rand/1

wypukła funkcja celu

● Wariancja punktów po sukcesji

● Równowagowa wariancja populacji:

● A dla alg. ewolucyjnego

(np. selekcja turniejowa, s=2, pc=0)

v_P(t+ 1)=k ( F) v_P(t ) 0< k< 1

v_P(∞)=0

v_P(∞)= π 2 vm

(40)

(41)

(42)

Algorytm ewolucyjny

● Algorytm ewolucyjny jest techniką adaptacji

rozkładu populacji

● Celem jest maksymalizacja wartości

oczekiwanej jakości generowanych punktów

● Środek populacji – najlepszy estymator

ekstremum lokalnego dla funkcji symetrycznej

(43)

Metoda EDA

Estimation of Distribution Algorithm

algorithm EDA initialize(m0,C0) H ← ∅ t ← 0 while ! stop Pt ← sample N (mt , Ct) H ← H ∪Pt Ot ← select ( Pt) (mt + 1, Ct + 1)← update(Ot , mt ,Ct) t ← t+ 1

(44)

Metoda EDA

Estimation of Distribution Algorithm

● UMDA (Univariate Marginal Distribution)

● Wartość oczekiwana i wariancja estymowana z

próby jako m(t+ 1)_j ←∑ i=1 μ w (i) P_ijt C (t+ 1)_jj ← ∑ i=1 μ w (i)( P_ijt −m(t+ 1)_j)2 C (t+ 1)_ij=0 i≠ j w (i)=q(Pi t ) ∑ q(P_it)

(45)

Metoda EDA

● Poinformowanie T ● Determinizm N

● Typ stanu zagregowany ● Wielkość modelu 1

● Lokalność generacji N

● Miękkość selekcji raczej N (selekcja?)

● Pamiętliwość tak, horyzont zależny od

metody update

(46)

(47)

(48)

(49)

(50)

(51)

(52)

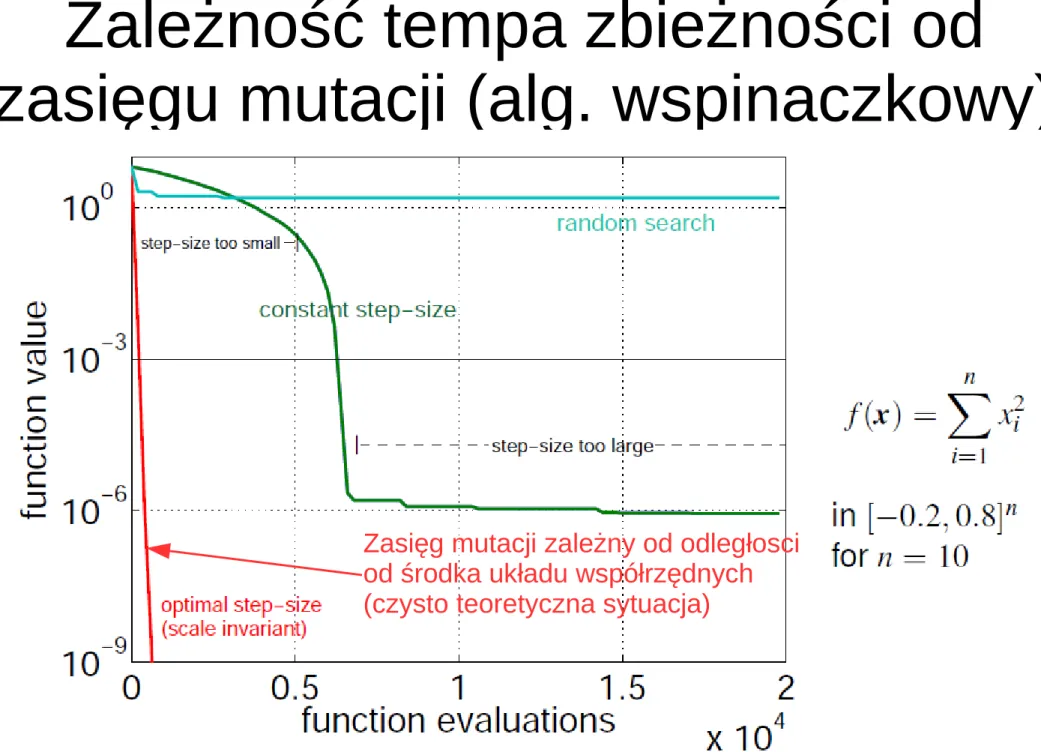
Zależność tempa zbieżności od

zasięgu mutacji (alg. wspinaczkowy)

Rysunek z: A. Auger, N. Hansen:

Zasięg mutacji zależny od odległosci od środka układu współrzędnych (czysto teoretyczna sytuacja)

(53)

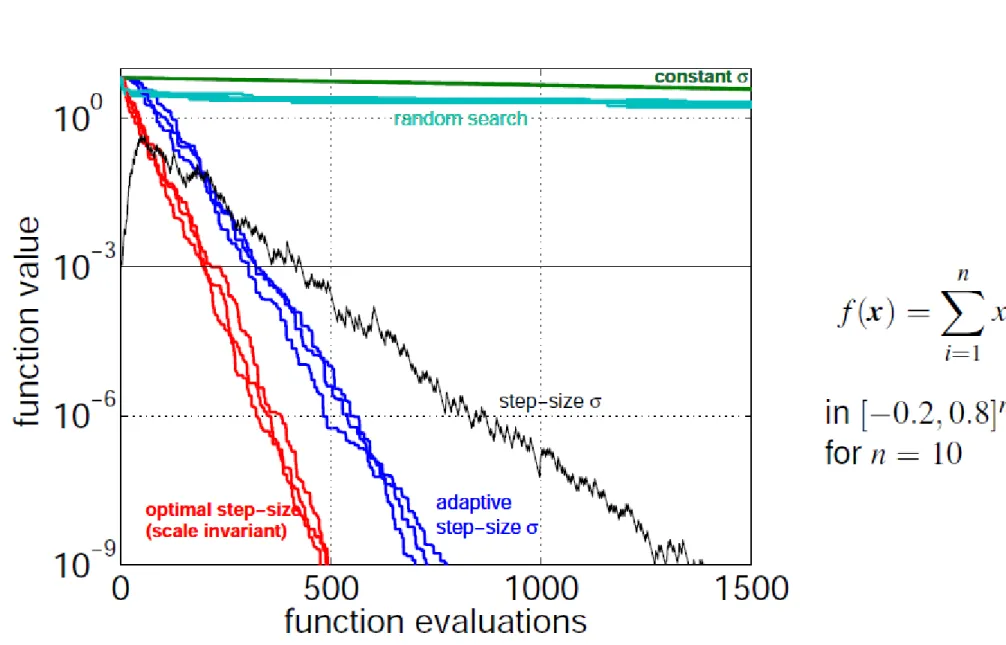
Zależność tempa zbieżności od

zasięgu mutacji (alg. wspinaczkowy)

CMA-ES — Evolution Strategies and Covariance Matrix Adaptation, tutorial, GECCO'2011

(54)

Reguła 1/5 liczby sukcesów

Średnia odległość mutantów

od rodzica(średnia długość kroku) jest równa standardowemu odchyleniu

Wraz ze wzrostem wariancji spada proporcja mutantów

o jakości lepszej od rodzica

Empirycznie dobrana wartość minimalizująca czas dojścia do

akceptowalnego poziomu wartości funkcji celu

(55)

● Liczba mutacji w wyniku których mutant jest

lepszy od rodzica powinna wynosić 1/5

● Sterowanie wariancją mutacji

● Pierwotnie stosowana do (1,lambda)-ES, czyli

algorytmu wspinaczkowego

σ (t+k )=a σ (t) gdy p(sukces)<0.2 σ (t +k)= 1

a σ (t ) gdy p(sukces)>0.2 0.817≤a≤1

(56)

(57)

Mutacja wariantowa z wyborem zależnym od poprawy procedure mutation(x ) j∗=select j where p_sel( j)=ns( j) ∑_k=1K n_s(k ) y=mutation( x , j∗) if (success( j∗)) n_s( j∗)=n_s( j∗)+ α n_s( j)=β⋅n_s( j) return ( y) ns – skumulowana liczba sukcesów dla każdego wariantu mutacji

(58)

Algorytm CMA-ES C (1)=I , p_c(1)=0, p_σ(1)=0 while ! stop generuj d_i(t )∼N (0,C (t )),i=1... λ oblicz q_i(t )=q(m(t )+σ (t )⋅d_i(t )) sortuj według q_i(t ) Δ (t )=_μ1 ∑μ_i=1 d_i(t ) m(t +1)=m(t )+σ (t )⋅Δ (t ) p_σ(t +1)=(1−c_σ) p_σ(t )+C−1/2√1−(1−c_σ)2√μ Δ(t ) p_c(t +1)=(1−c_c) p_c(t )+√1−(1−c_c)2√μ Δ (t ) σ (t +1)=σ (t )⋅exp

(

cσ d_σ

(

‖p_σ‖ E‖N (0, I )‖−1

)

C (t +1)=(1−c₁−c_μ)C (t )+c₁ p_c(t +1) p_c(t +1)T+c_μ∑_i=1μ d_i(t )d_i(t )T t ←t +1 Przestrzeń x Przestrzeń skojarzona

(59)

Adaptacja skumulowanego kroku algorytm CSA-ES

(60)

Adaptacja skumulowanego kroku algorytm CSA-ES c_σ≈4 /n , d_σ≈1, p_σ=0 while ! stop generuj d_i(t)∼N (0, I ),i=1. .. λ oblicz q_i(t)=q₍m(t)+ σ (t)⋅d_i(t )₎ sortuj według q_i(t) Δ (t )=_μ1 ∑ i=1 μ d_i(t) m(t+ 1)=m(t)+ σ (t )⋅Δ (t ) p_σ(t+ 1)=(1−c_σ) p_σ(t )+ √1−(1−c_σ)2√μ Δ (t) σ (t+ 1)=σ (t )⋅exp

(

cσ d_σ

(

∥p_σ∥ E∥N (0, I )∥−1

)

t ← t+ 1 Przestrzeń x Przestrzeń skojarzona

(61)

Adaptacja skumulowanego kroku algorytm CSA-ES

CMA-ES — Evolution Strategies and Covariance Matrix Adaptation, tutorial, GECCO'2011 Trajektoria punktu środkowego

(62)

Modyfikacja macierzy kowariancji algorytm CMA-ES (wersja 0)

C (1)=I while ! stop generuj d_i(t)∼N (0,C (t )), i=1... λ oblicz q_i(t)=q ₍m(t )+σ (t)⋅d_i(t)₎ sortuj według q_i(t) Δ (t)=_μ1 ∑μ_i=1 d_i(t) m(t+1)=m(t)+σ (t)⋅Δ (t) C (t +1)=(1−c_cov)C (t )+c_covμ Δ (t)Δ (t )T t ← t +1 Przestrzeń x

(63)

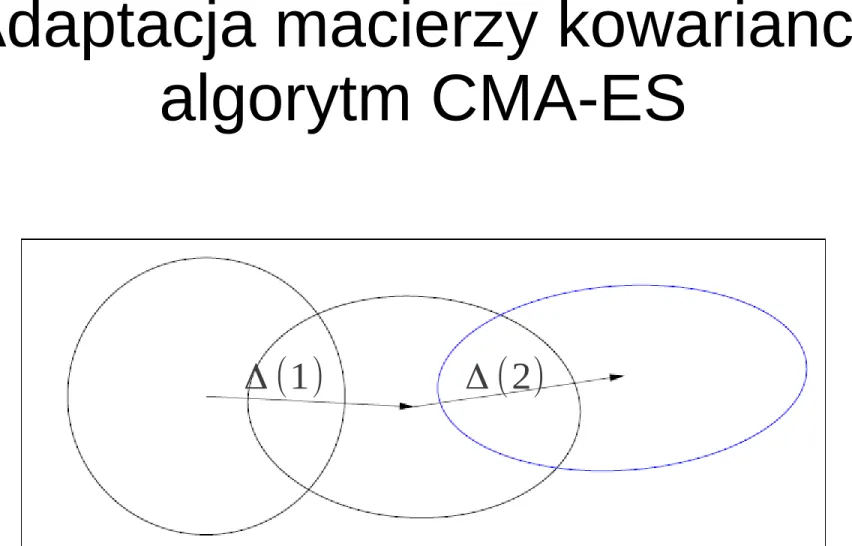
Adaptacja macierzy kowariancji algorytm CMA-ES

CMA-ES — Evolution Strategies and Covariance Matrix Adaptation, tutorial, GECCO'2011 Δ (t)=_μ1 ∑μ_i=1 d_i(t )

d_i(t)∼σ (t )⋅N (0,C (t )),i=1. .. λ

(64)

Adaptacja macierzy kowariancji algorytm CMA-ES

(65)

C (1)=I , p_c(1)=0 while ! stop generuj d_i(t )∼N (0,C (t )), i=1... λ oblicz q_i(t )=q ₍m(t )+σ (t )⋅d_i(t)₎ sortuj według q_i(t) Δ (t)=_μ1 ∑ i=1 μ d_i(t ) m(t +1)=m(t)+σ (t)⋅Δ(t ) p_c(t +1)=(1−c_c) p_c(t )+√1−(1−c_c)2√μ Δ (t) C (t +1)=(1−c_cov)C (t )+c_cov p_c(t +1) p_c(t +1)T t ← t +1 bezwładność Przestrzeń x

(66)

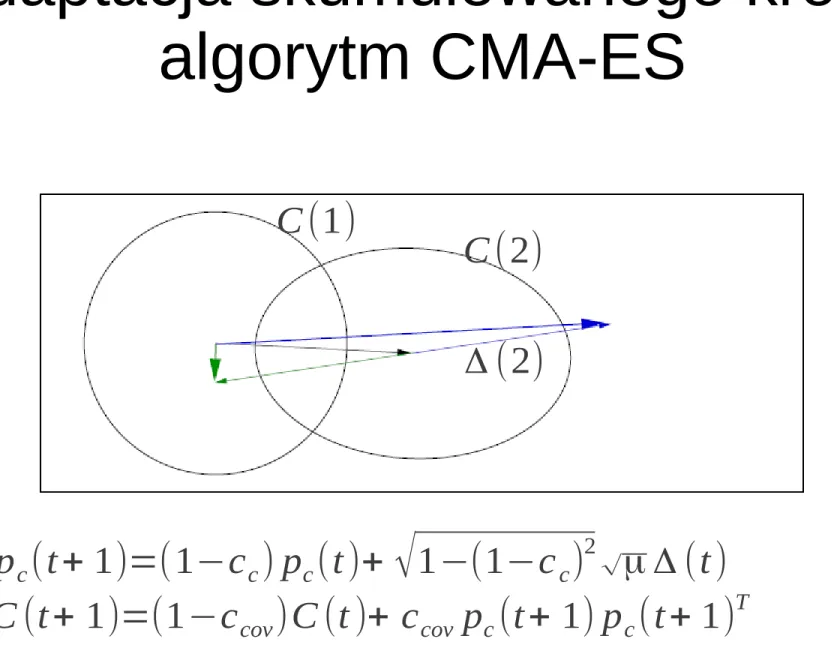
Adaptacja skumulowanego kroku algorytm CMA-ES

p_c(t+ 1)=(1−c_c) p_c(t)+ √1−(1−c_c)2√μ Δ (t)

C (t+ 1)=(1−c_cov)C (t )+ c_cov p_c(t+ 1) p_c(t+ 1)T

Δ (2)

C (2) C (1)

(67)

C (1)=I while ! stop generuj d_i(t)∼N (0,C (t )), i=1... λ oblicz q_i(t)=q (m(t )+σ (t)⋅d_i(t)) sortuj według q_i(t) Δ (t)=_μ1 ∑μ_i=1 d_i(t) m(t+1)=m(t)+σ (t)⋅Δ(t)

C (t +1)=(1−c_cov)C (t )+c_cov ∑_i=1μ d_i(t) d_i(t )T t ← t +1

uwzględnienie wielu wektorów różnic

Wszystkie operacje w przestrzeni x

(68)

Pełny CMA-ES C (1)=I , p_c(1)=0, p_σ(1)=0 while ! stop generuj d_i(t )∼N (0,C (t )),i=1... λ oblicz q_i(t )=q(m(t )+σ (t )⋅d_i(t )) sortuj według q_i(t ) Δ (t )=_μ1 ∑μ_i=1 d_i(t ) m(t +1)=m(t )+σ (t )⋅Δ (t ) p_σ(t +1)=(1−c_σ) p_σ(t )+C−1/2√1−(1−c_σ)2√μ Δ(t ) p_c(t +1)=(1−c_c) p_c(t )+√1−(1−c_c)2√μ Δ (t ) σ (t +1)=σ (t )⋅exp

(

cσ d_σ

(

‖p_σ‖ E‖N (0, I )‖−1

)

C (t +1)=(1−c₁−c_μ)C (t )+c₁ p_c(t +1) p_c(t +1)T+c_μ∑_i=1μ d_i(t )d_i(t )T t ←t +1 Przestrzeń x Przestrzeń skojarzona

(69)

Pełny CMA-ES C (1)=I , p_c(1)=0, p_σ(1)=0 while ! stop generuj d_i(t )∼N (0,C (t )),i=1... λ oblicz q_i(t)=q(m(t)+σ (t )⋅d_i(t)) sortuj według q_i(t) Δ (t )=_μ1 ∑_i=1μ d_i(t ) m(t +1)=m(t)+σ (t )⋅Δ (t) p_σ(t +1)=(1−c_σ) p_σ(t)+√1−(1−c_σ)2√μC−1/2 Δ(t) σ (t +1)=σ (t)⋅exp

(

cσ d_σ

(

‖p_σ‖ E‖N (0, I )‖−1

)

p_c(t +1)=(1−c_c) p_c(t )+√1−(1−c_c)2√μ Δ (t ) C (t +1)=(1−c₁−c_μ)C (t )+ c₁ p_c(t +1) p_c(t +1)T+c_μ∑μ_i=1 d_i(t)d_i(t )T t ← t +1

(70)

CMAES

Covariance Matrix Adaptation Evolution Strategy

(71)

CMAES

(72)

CMAES

(73)

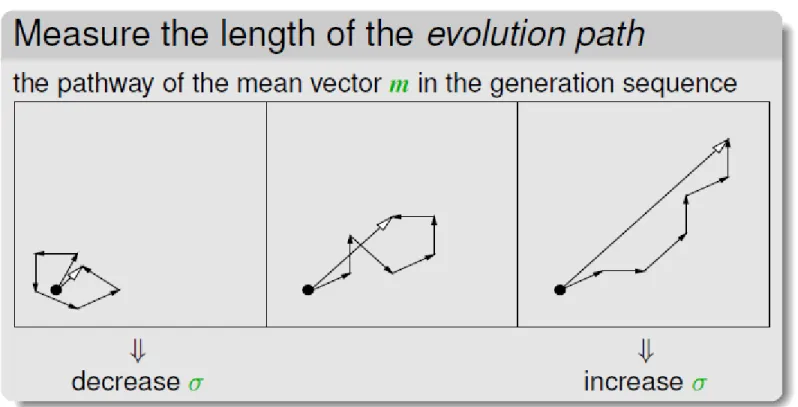
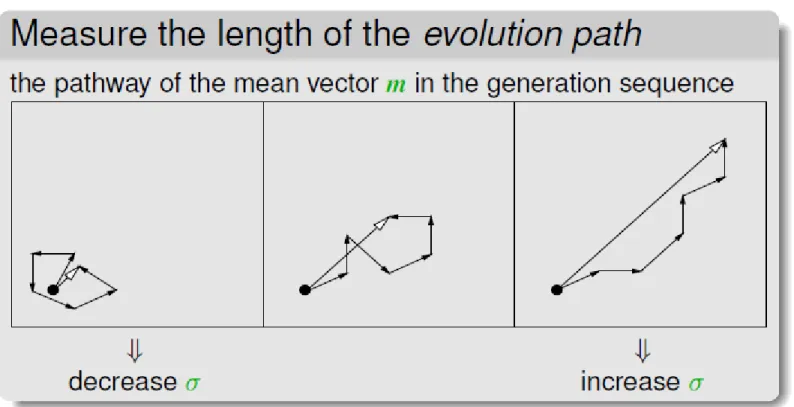
CMAES

evolution path

Podążanie w +/- zgodnych kierunkach

(74)

CMAES

Na podstawie selekcji adaptuje się kształt macierzy kowariancji

Jej skala zależy od ścieżki ewolucji

(75)

(76)

(77)

(78)

Przeszukiwanie rojem cząstek

algorytm particle swarm inicjuj P0 ← {P_1,0 P₂0... P_μ0} inicjuj V 0← {V_1,0 V ₂0...V _μ0} H ← P0 t ← 0 while ! stop g(t )← arg max i ,t q( Pi t ) for (i∈1:μ) b_i(t) ← arg max t q (Pi t ) V _it + 1 ← a(V _it+ c(r_g(g(t )−P_it)+ r_l(b_i(t )−P_it))) P_it+ 1 ← P_it+ V_it+ 1 H ← H ∪Pt + 1 a, c są parametrami typowo a=0.73, c=2.05 r_g,r_l~ U (0,1)

(79)

(80)

(81)

(82)

(83)

(84)