Definicja całki oznaczonej Riemanna

(1)

Definicja całki oznaczonej

Riemanna

Autorzy:

Witold Majdak

(2)

Definicja całki oznaczonej Riemanna

Autor: Witold Majdak

Niech będzie funkcją ograniczoną. Dla każdej liczby naturalnej wybierzmy pewne elementy należące do przedziału , które spełniają następujące zależności:

Zbiór nazywamy -tym podziałem-tym podziałem przedziału odpowiadającym ustalonej liczbie . Dla -tego podziału przedziału oznaczmy przez długość dowolnego podprzedziału , tzn.

gdzie . Liczbę nazywamy średnicą podprzedziału . Niech będzie największą ze średnic wszystkich podprzedziałów występujących w -tym podziale przedziału , czyli

Następnie dla każdego wybierzmy pewien element zwany punktem pośrednimpunktem pośrednim podziału .

DEFINICJA

Definicja 1: n-ta suma całkowa Riemanna

Niech

Powyższą sumę nazywamy -tą sumą całkową Riemanna-tą sumą całkową Riemanna funkcji w przedziale .

DEFINICJA

Definicja 2: Normalny ciąg podziałów przedziału

Mówimy, że ciąg podziałów przedziału jest normalnynormalny, jeżeli .

Oznacza to de facto, że gdy rośnie, to uzyskane podprzedziały (czyli części, na które dzielimy przedział ) są coraz mniejsze.

f : [a, b] → R

n

x

0

, …,

x

n

[a, b]

a =

x

0

<

x

1

< … <

x

n

= b.

= { , , …, }

Δ

n

x

0

x

1

x

n

[a, b]

n

[a, b]

Δx

k

[

x

k−1

, ]

x

k

Δ =

x

k

x

k

−

x

k−1

,

k ∈ {1, 2, …, n}

Δx

k

[

x

k−1

, ]

x

k

δ

n

[

x

k−1

, ]

x

k

n

[a, b]

= max{Δ : k = 1, 2, …, n}.

δ

n

x

k

k ∈ {1, 2, …, n}

ξ

k

∈ [

x

k−1

, ]

x

k

Δ

n

=

f( )Δ .

S

n

∑

k=1 n

ξ

k

x

k

S

n

f

[a, b]

(Δ

n

)

∞n=1

[a, b]

_n→∞

lim

δ

n

= 0

n

[a, b]

(3)

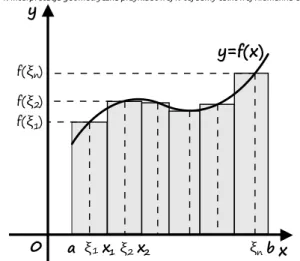
Rysunek 1: Interpretacja geometryczna przykładowej -tej sumy całkowej Riemanna dla

Rysunek 2: Interpretacja geometryczna przykładowej -tej sumy całkowej Riemanna

Przejdźmy do definicji całki oznaczonej Riemanna funkcji ograniczonej.

DEFINICJA

Definicja 3: Całka oznaczona Riemanna

Jeżeli dla każdego normalnego ciągu podziałów przedziału ciąg -tych sum całkowych Riemanna jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów pośrednich ( ), to granicę tę nazywamy całką oznaczoną Riemannacałką oznaczoną Riemanna funkcji na przedziale i oznaczamy symbolem , tzn.

Rysunek 3: Interpretacja geometryczna całki oznaczonej Riemanna funkcji

W powyższej całce liczbę nazywamy dolną granicą całkowaniadolną granicą całkowania, liczbę górną granicą całkowaniagórną granicą całkowania, natomiast funkcjąfunkcją podcałkową

podcałkową. Jeżeli i są takimi liczbami rzeczywistymi, że , to przyjmujemy, że

Ponadto dla liczby rzeczywistej przyjmujemy, że

n n = 4 n

(Δ

n

)

∞n=1

[a, b]

(S

n

)

∞n=1

n

ξ

k

k = 1, …, n

f

[a, b]

∫

b

f(x)dx

a

I = f(x)dx :=

∫

.

a b

lim

n→∞

S

n f

a

b

f

a b

a < b

f(x)dx := − f(x)dx.

∫

b a

∫

a b

a

f(x)dx := 0.

∫

a a

(4)

Przyjrzyjmy się, w jaki sposób można obliczyć całkę oznaczoną Riemanna korzystając z jej definicji.

PRZYKŁAD

Przykład 1:

Obliczmy całkę oznaczoną funkcji stałej przyjmującej wartość na przedziale . Funkcja jest ograniczona. Rozważając dowolny ciąg podziałów normalnych odcinka niezależnie od wyboru punktów pośrednich otrzymujemy

Wykażemy teraz, że nie każda funkcja ograniczona jest całkowalna.

PRZYKŁAD

Przykład 2:

Zdefiniujmy tzw. funkcję Dirichletafunkcję Dirichleta za pomocą następującego przepisu:

gdzie jest zbiorem liczb wymiernych.

Funkcja jest ograniczona. Rozważmy dowolny przedział zawarty w . Dla każdej liczby naturalnej

wybierzmy dowolny podział odcinka tak, aby ciąg był normalnym ciągiem podziałów tego odcinka. Następnie wybierzmy ciąg punktów pośrednich tego podziału, które należą do zbioru liczb wymiernych, i

utwórzmy -tą sumę całkową Riemanna . Okazuje się, że skoro dla wszystkich liczb wymiernych funkcja przyjmuje stale wartość 1, to

Podobnie, wybierzmy ciąg punktów pośrednich ustalonego podziału w taki sposób, aby należały one do zbioru liczb niewymiernych, oraz utwórzmy -tą sumę całkową Riemanna . Wiadomo, że dla dowolnej liczby niewymiernej funkcja przyjmuje wartość 0, zatem

Granice obu ciągów -tych sum całkowych Riemanna są różne, a więc całka nie istnieje.

f

c ∈ R

[a, b]

f

(Δ

n

)

∞n=1

[a, b]

ξ

k

cdx =

cΔ = c

Δ = c

[( − ) + … + ( −

)] = c

(b − a) = c(b − a).

∫

a b

lim

n→∞_k=1

∑

n

x

k _n→∞

lim

∑

k=1 n

x

k _n→∞

lim

x

1

x

0

x

n

x

n−1 _n→∞

lim

f(x) = { 1,

_0,

gdy x ∈ Q,

_{gdy x ∈ R ∖ Q,}

(Q)

(f)

[a, b]

(R)

(n)

( )

Δ

n

[a, b]

(

Δ

n

)

∞n=1

)

((

ξ

k

)

nk=1

)

(n)

( )

S

n

(f)

=

f( )Δ =

1 ⋅ Δ = 1.

S

n

∑

k=1 n

ξ

k

x

k

∑

k=1 n

x

k

(

˜)

ξ

k nk=1

)

(n)

( )

S

˜

n

(f)

=

f( )Δ =

0 ⋅ Δ = 0.

S

˜

n

∑

k=1 n

ξ

k

˜ x

k

∑

k=1 n

x

k

(n)

( f(x)dx)

∫

b a

(5)

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: Warunek wystarczający całkowalności

Warunek wystarczający całkowalności

Jeżeli funkcja jest ciągła, to jest ona całkowalna w przedziale .

PRZYKŁAD

Przykład 3:

Obliczmy całkę oznaczoną , korzystając z jej definicji. Funkcja podcałkowa jest oczywiście ciągła, zatem na mocy twierdzenia Warunek wystarczający całkowalności całka ta istnieje. Wobec tego przy dowolnym wyborze ciągu podziałów normalnych odcinka oraz układu punktów pośrednich ciąg -tych sum całkowych Riemanna

jest zawsze zbieżny do tej samej granicy. Możemy więc wybrać jeden szczególny ciąg podziałów normalnych odcinka oraz układy punktów pośrednich w taki sposób, aby wygodnie było obliczyć granicę . Otóż dla ustalonego wybierzmy punkty podziału oraz punkty pośrednie

. Wówczas każdy z odcinków ma tę samą długość . Oznacza to, że

a w rezultacie . Uwzględniając to, że

możemy wykonać następujące obliczenia:

mając na uwadze, że jest sumą kolejnych liczb .

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: o całkowalności funkcji mającej skończoną liczbę punktów

o całkowalności funkcji mającej skończoną liczbę punktów

nieciągłości

Jeżeli funkcja ma skończoną liczbę punktów nieciągłości w przedziale , to jest ona całkowalna w tym przedziale.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko

f : [a, b] → R

[a, b]

( xdx)

∫

₁3

(f(x) = x)

[1, 3]

(n)

(

S

n

)

∞n=1

)

(

Δ

n

)

∞n=1

)

[1, 3]

(

_n→∞

lim

S

n

)

(n)

( = 1 + k)(k = 0, …, n)

x

k _n2

(x = )(k = 1, …, n)

i

k

x

k

[

x

k−1

, ]

x

k

(Δ = )

x

k n2

= max{Δ : k = 1, 2, …, n} = ,

δ

n

x

k _n2

(

lim

= 0)

n→∞

δ

n

=

f( )Δ =

(1 + k) ,

S

n

∑

k=1 n

ξ

k

x

k

∑

k=1 n ₂ n 2n

xdx

∫

1 3

=

lim

=

(1 + k) =

( +

k)

n→∞

S

n n→∞

lim

∑

_k=1 n

₂

n

2

n→∞

lim

∑

_k=1 n

₂

n

4

2

=

lim

(

1 +

k) =

(2 + 2

) = 4,

n→∞

2 n

∑

_k=1 n

₄

n

2

∑

k=1 n

lim

n→∞

1 + n

n

(n+1)n 2

1, …, n

f : [a, b] → R

[a, b]

(6)

na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-16 09:19:03

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=85b589b813eb545a4ae1d907f8584bc9