Funkcje cyklometryczne. Definicje, wykresy, podstawowe własności

(1)

Funkcje cyklometryczne.

Definicje, wykresy,

podstawowe własności

Autorzy:

Anna Barbaszewska-Wiśniowska

2019

(2)

Funkcje cyklometryczne. Definicje, wykresy, podstawowe własności

Autor: Anna Barbaszewska-Wiśniowska

UWAGA

Uwaga 1: O różnowartościowości pewnych zawężeń funkcji trygonometrycznych

Funkcje trygonometryczne jako funkcje okresowe nie są funkcjami różnowartościowymi. Mamy wiele (nieskończenie wiele) możliwości utworzenia ich różnowartościowych zawężeń. Szczególną rolę odgrywają następujące zawężenia (restrykcje):

Powyższe zawężenia są funkcjami różnowartościowymi oraz „na”, czyli są bijekcjami, zatem posiadają funkcje odwrotne. Te funkcje odwrotne nazywamy funkcjami cyklometrycznymifunkcjami cyklometrycznymi .

DEFINICJA

Definicja 1: Funkcja arkus sinus

Funkcją arkus sinus

Funkcją arkus sinus (oznaczaną arcsinarcsin) nazywamy funkcje odwrotną do funkcji sinus zawężonej do przedziału domkniętego

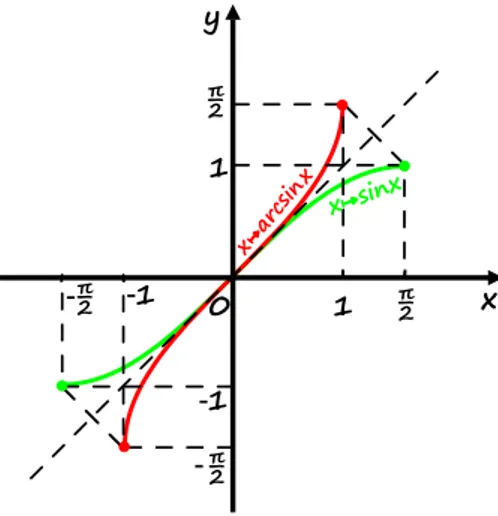
Dziedziną funkcji arkus sinusarkus sinus jest przedział , zaś zbiorem wartości przedział . Wykres funkcji arcsinarcsin powstaje poprzez odbicie symetryczne względem prostej wykresu zawężonej funkcji sinussinus

Rysunek 1: Funkcja arkus sinus

: [ , ] ∋ x → sin x ∈ [−1, 1],

sin

_{|[− , ]}π 2 π2 −π 2 π2

: [0, π] ∋ x → cos x ∈ [−1, 1],

cos

|[0,π]

: ( , ) ∋ x → tg x ∈ R,

tg

|(− , )π 2 π2 −π 2 π2

: [0, π] ∋ x → ctg x ∈ R.

ctg

|[0,π]

[ , ]

−π 2 π2

arcsin := (

sin

_{|[− , ]}π

)

2 π2 −1

[−1, 1]

[ , ]

−π 2 π2

y = x

(

sin

_{|[− , ]}π

)

2 π2

(3)

UWAGA

Uwaga 2: Własności funkcji arkus sinus

Podstawowe własności funkcji arkus sinusarkus sinus wynikają z faktu, że jest to funkcja odwrotna do odpowiednio zawężonej funkcji sinus

sinus i z ogólnych własności funkcji wzajemnie odwrotnych. Na przykład z tego, że dla każdego , dla każdego wynika, że

Podobnie można skomentować pozostałe własności

Funkcje jest funkcją rosnącą jako odwrotna do rosnącego zawężenia funkcji sinussinus . Funkcja jest funkcją nieparzystą.

Funkcja jest funkcją ograniczoną dla każdego .

DEFINICJA

Definicja 2: Funkcja arkus kosinus

Funkcją arkus kosinus

Funkcją arkus kosinus (oznaczaną arccosarccos) nazywamy funkcję odwrotną do funkcji kosinus zawężonej do przedziału domkniętego .

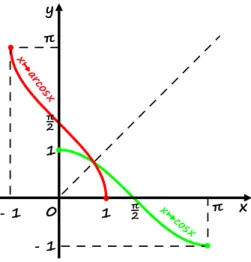
Dziedziną funkcji arkus kosinus jest przedział , zaś zbiorem wartości przedział . Wykres funkcji arccos powstaje poprzez odbicie symetryczne względem prostej wykresu zawężonej funkcji kosinus

(f(x)) = x

f

−1

_{x ∈ X}

f(

f

−1

(x)) = x

_{x ∈ Y}

arcsin(sin x) = x dla x ∈ [− , ].

π 2 π2

sin(arcsinx) = x dla x ∈ [−1, 1].

arcsinx = w ⇔ sin w = x i w ∈ [− , ], x ∈ [−1, 1].

π 2 π2

x ↦ arcsin x

(

sin

_{|[− , ]}π

)

2 π2

x ↦ arcsin x

arcsin(−x) = − arcsinx, x ∈ [−1, 1].

x ↦ arcsin x

| arcsinx| ≤

π 2

x ∈ [1, −1]

[0, π]

arccos := (

cos

|[0,π]

)

−1

.

[−1, 1]

[0, π]

y = x

(

cos

|[0,π]

)

(4)

Rysunek 2: Funkcja arkus kosinus

UWAGA

Uwaga 3: Własności funkcji arkus kosinus

Podstawowe własności funkcji arkus kosinus wynikają z faktu, że jest to funkcja odwrotna do odpowiednio zawężonej funkcji kosinus i z ogólnych własności funkcji wzajemnie odwrotnych. Na przykład z tego, że dla każdego

, dla każdego , wynika, że

Funkcja jest funkcją malejącą jako odwrotna do malejącego zawężenia funkcji kosinus . Funkcja jest funkcją ograniczoną, czyli

Funkcja nie jest funkcją parzystą, ani nieparzystą.

(f(x)) = x

f

−1

x ∈ X f(

f

−1

(x)) = x

_{x ∈ Y}

arccos(cos x) = x, dla x ∈ [0, π].

cos(arccosx) = x, dla x ∈ [−1, 1].

arccosx = w ⇔ cos w = x i w ∈ [0, π], x ∈ [−1, 1].

x ↦ arccosx

(

cos

|[0,π]

)

x ↦ arccosx

0 ≤ arccosx ≤ π, dla ka

ż

dego x ∈ [−1, 1].

x → arccosx

(5)

DEFINICJA

Definicja 3: Funkcja arkus tangens

Funkcją arkus tangens

Funkcją arkus tangens (oznaczaną arctgarctg) nazywamy funkcje odwrotną do funkcji tangens zawężonej do przedziału otwartego ,

Dziedziną funkcji arkus tangens jest zbiór liczb rzeczywistych, zaś zbiorem wartości tej funkcji jest przedział otwarty . Wykres funkcji arccos powstaje poprzez odbicie symetryczne względem prostej wykresu zawężonej funkcji

tangens .

Rysunek 3: Funkcja arkus tangens

UWAGA

Uwaga 4: Własności funkcji arkus tangens

Podstawowe własności funkcji arkus tangens wynikają z faktu, że jest to funkcja odwrotna do odpowiednio zawężonej funkcji tangens i z ogólnych własności funkcji wzajemnie odwrotnych. Na przykład z tego, że , dla każdego

, , dla każdego wynika, że

Funkcja jest funkcją rosnącą jako odwrotna do rosnącego zawężenia funkcji tangens . Funkcja jest funkcją ograniczoną, czyli

Funkcja jest funkcją nieparzystą,

(− , )

π 2 π2

arctg := (

tg

|(− , )π

.

2 π2

)

−1

(− , )

π 2 π2

y = x

(

tg

_{|(− , )}π

)

2 π2

(f(x)) = x

f

−1

x ∈ X

f

−1

(x) = x

_{x ∈ Y}

arctg(tg x) = x dla x ∈ (− , ).

π 2 π2

tg(arctg x) = x dla x ∈ R,

arctg x = w ⇔ tg w = x i w ∈ (− , ), x ∈ R.

π 2 π2

x ↦ arctg x

(

tg

_{|(− , )}π

)

2 π2

x ↦ arctg x

|arctgx| ≤ , dla ka

π ż

dego x ∈ R

2

x ↦ arctg x

(6)

DEFINICJA

Definicja 4: Funkcja arkus kotangens

Funkcją arkus kotangens (oznaczaną arcctg)

Funkcją arkus kotangens (oznaczaną arcctg) nazywamy funkcje odwrotną do funkcji kotangens zawężonej do przedziału otwartego

Dziedziną funkcji arkus kotangens jest cały zbiór liczb rzeczywistych, zaś zbiorem wartości tej funkcji jest przedział otwarty . Wykres funkcji arcctg powstaje poprzez odbicie symetryczne względem prostej wykresu zawężonej funkcji kotangens .

Rysunek 4: Funkcja arkus kotangens

(0, π)

arcctg := (

ctg

|(0,π)

)

−1

(0, π)

y = x

(7)

(1) (2)

UWAGA

Uwaga 5: Własności funkcji arkus kotangens

Podstawowe własności funkcji arkus kotangens wynikają z faktu, że jest to funkcja odwrotna do odpowiednio zawężonej funkcji kotangens i z ogólnych własności funkcji wzajemnie odwrotnych. Na przykład z tego, że , dla każdego

, dla każdego wynika, że

Funkcja jest funkcją malejącą jako odwrotna do malejącego zawężenia funkcji kotangens . Funkcja jest funkcją ograniczoną.

Funkcja nie jest funkcją parzystą ani nieparzystą.

UWAGA

Uwaga 6: O związkach pomiędzy funkcjami cyklometrycznymi

Pomiędzy funkcjami cyklometrycznymi (podobnie jak pomiędzy funkcjami trygonometrycznymi) zachodzi wiele związków. Niektóre z nich, jak dwie tożsamości cyklometryczne podane poniżej można bardzo łatwo zauważyć. I tak spostrzegamy, że po przesunięciu "do góry" wykresu funkcji arkus sinus o wektor , a następnie przekształceniu przez symetrie względem osi otrzymujemy wykres funkcji arkus kosinus. Podobnie postępując z wykresem funkcji arkus tangens otrzymujemy wykres funkcji arkus kotangens.

TWIERDZENIE

Twierdzenie 1: Związki pomiędzy funkcjami cyklometrycznymi

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

(f(x)) = x

f

−1

x ∈ X f(

f

−1

(x)) = x

_{x ∈ Y}

arcctg(ctg x) = x, dla x ∈ (0, π).

ctg(arcctg x) = x, dla x ∈ R,

arcctg x = w ⇔ ctg w = x i w ∈ (0, π), x ∈ R.

x ↦ arcctg x

(

ctg

|(0,π)

)

x ↦ arcctg x

0 ≤ arcctg x ≤ π, dla ka

ż

dego x ∈ R.

x ↦ arcctg x

= [0, ]

v⃗

π

2

0y⃗

arcsinx + arccosx = , dla ka

π₂ ż

dego x ∈ [−1, 1]

(8)

Data generacji dokumentu: 2019-04-15 10:06:29

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=00f0c8f47a7588821f8bf5b75ce7b0b6