Stabilność rozwiązań równań różniczkowych zwyczajnych

Równania różniczkowe

zwyczajne

Autorzy:

Vsevolod Vladimirov

Julian Janus

2019

Spis treści

Spis treści

Skalarne równania różniczkowe zwyczajne. Pojęcia wstępne Równania różniczkowe rzędu pierwszego o zmiennych rozdzielonych

Równania różniczkowe rzędu pierwszego, które sprowadzają się do równań o zmiennych rozdzielonych Przykłady równań różniczkowych wykorzystywanych w naukach przyrodniczych

Zagadnienie początkowe (zagadnienie Cauchy'ego). Poprawność zadania warunków początkowych Liniowe równania różniczkowe rzędu pierwszego

Metoda Eulera

Równania różniczkowe liniowe wyższych rzędów - podstawowe pojęcia Liniowa zależność i niezależność funkcji

Fundamentalny zbiór rozwiązań dla równań różniczkowych liniowych wyższych rzędów

Wyznaczanie fundamentalnego zbioru rozwiązań równań różniczkowych liniowych jednorodnych drugiego rzędu, gdy znamy jedno rozwiązanie

Wyznaczanie fundamentalnego zbioru rozwiązań równań różniczkowych liniowych jednorodnych drugiego rzędu o stałych współczynnikach

Wyznaczanie fundamentalnego zbioru rozwiązań równań różniczkowych liniowych jednorodnych o stałych współczynnikach rzędu wyższego niż dwa

Rozwiązywanie równań różniczkowych liniowych niejednorodnych wyższych rzędów metodą uzmieniania stałych Przykłady rozwiązywania równań różniczkowych liniowych niejednorodnych wyższych rzędów o stałych współczynnikach metodą uzmienniania stałych

Rozwiązywanie równań różniczkowych liniowych niejednorodnych wyższych rzędów o stałych współczynnikach metodą przewidywań

Przykłady zastosowań równań różniczkowych liniowych rzędu drugiego

Równania różniczkowe rzędu drugiego sprowadzalne do równań rzędu pierwszego Równania różniczkowe Eulera

Rozwiązywanie układów równań różniczkowych metodą operatorową (sprowadzanie układu równań do równania zwyczajnego rzędu wyższego)

Przykłady rozwiązywania układów równań różniczkowych metodą operatorową

Przykład rozwiązywania układów równań z warunkami początkowymi metodą operatorową Układ normalny równań różniczkowych rzędu pierwszego

Układy równań różniczkowych liniowych rzędu pierwszego

Rozwiązywanie układów równań liniowych jednorodnych o stałych współczynnikach, gdy wartości własne są rzeczywiste i jednokrotne

Rozwiązywanie układów równań liniowych jednorodnych o stałych współczynnikach, gdy wartości własne są jednokrotne, ale nie wszystkie rzeczywiste

Rozwiązywanie układów równań liniowych jednorodnych o stałych współczynnikach, gdy macierz układu jest diagonalizowalna

Rozwiązywanie układów równań liniowych jednorodnych o stałych współczynnikach, gdy macierz układu nie jest diagonalizowalna

Przykłady rozwiązywania układów równań liniowych jednorodnych o stałych współczynnikach, gdy macierz układu nie jest diagonalizowalna

Macierz wykładnicza i jej własności Wyznaczanie macierzy wykładniczej

Przykłady rozwiązywania układów równań liniowych jednorodnych o stałych współczynnikach przy użyciu macierzy wykładniczej

Przykłady rozwiązywania układów równań liniowych niejednorodnych o stałych współczynnikach metodą uzmienniania stałych

Rozwiązywanie układów równań liniowych niejednorodnych o stałych współczynnikach metodą przewidywań

Przykłady rozwiązywania układów równań liniowych niejednorodnych o stałych współczynnikach metodą przewidywań Przykłady zastosowania układów równań różniczkowych

Układy dynamiczne. Klasyfikacja punktów stacjonarnych na płaszczyźnie Pojęcie całkowania jakościowego. Układy hamiltonowskie na płaszczyźnie Analiza jakościowa równania Duffinga

Analiza jakościowa równania opisującego ruch płaski wahadła matematycznego Nieliniowe rozwiązania okresowe w dwuwymiarowym układzie dynamicznym Warunki powstania cyklu granicznego w równaniu typu Van der Pola Skalarne quasiliniowe równanie cząstkowe

Rozwiązanie ogólne równania quasiliniowego w przypadku funkcji dwóch zmiennych niezależnych Przykłady znajdowania rozwiązania ogólnego równania quasiliniowego o dwóch zmiennych niezależnych Rozwiązywanie zagadnienia początkowego równania quasiliniowego o dwóch zmiennych niezależnych

Skalarne równanie quasiliniowe dla funkcji n zmiennych niezależnych

Twierdzenia o istnieniu i jednoznaczności dla równań różniczkowych zwyczajnych Stabilność rozwiązań równań różniczkowych zwyczajnych

(1)

(2)

(3)

(4)

Skalarne równania różniczkowe zwyczajne. Pojęcia

Skalarne równania różniczkowe zwyczajne. Pojęcia

wstępne

wstępne

Czym są równania różniczkowe i do czego one służą? Zacznijmy od pewnych analogii. W kursie matematyki elementarnej rozwiązuje się równania algebraiczne. Przykładem może służyć układ równań liniowych

lub równanie

zwane równaniem kwadratowym. Rozwiązywanie obu równań polega na znalezieniu liczb, które po podstawieniu do

odpowiednich równań czyniły by z nich tożsamości. W przypadku układu równań w naszym przypadku są to liczby , które są określone jednoznacznie. Podane równanie kwadratowe spełniają dwie liczby: oraz . W przypadku równań różniczkowych nie chodzi o znalezienie rozwiązań liczbowych. Rozwiązaniami są funkcje różniczkowalne spełniające równanie, przy czym niejednoznaczność rozwiązania jest raczej regułą niż wyjątkiem. Przejdźmy jednak do definicji.

DEFINICJA

Definicja 1:

Definicja 1:

Równaniem różniczkowym zwyczajnym (RRZ) nazywamy równanie

gdzie jest funkcją różniczkowalną w każdym ze swoich argumentów. W równaniu ( 2 ) niewiadomą jest krotnie różniczkowana funkcja , zatem równanie ( 2 ) jest równaniem funkcyjnym.

Jeżeli jesteśmy w stanie rozwiązać równanie ( 2 ) względem ostatniej zmiennej, wówczas możemy go napisać w postaci równoważnej

zwanej postacią kanoniczną skalarnego RRZ -tego rzędu.

Rozwiązać równanie ( 2 ) oznacza znaleźć razy różniczkowalną funkcję , która, będąc podstawioną do równania ( 2 ), uczyni z niego tożsamość. Rzędem równania ( 2 ) nazywamy największy rząd pochodnej szukanej funkcji , występującej w tym równaniu.

Najprostsze równanie różniczkowe dyktuje problem znalezienia funkcji pierwotnej do zadanej funkcji ciągłej :

Zatem rozwiązanie tego równania dane jest wzorem

opisującym nieskończenie wiele funkcji pierwotnych funkcji , rózniących się o dowolną stałą.

{ x + y = 1,

_{x − y = 0}

− x − 6 = 0,

x

x = y = 1/2

x = 3

x = −2

F(t, x(t), (t), …,

x

_x

(t)) = 0,

F

n−

x = x(t)

= Ψ (t, x(t), x(t), . . . ,

) ,

x

_x

n

n

x = φ(t)

x = φ(t)

x(t)

f(t)

= f(t).

x(t) = ∫ f(t) dt,

x(t)

(5) (6) (7) - 4 - 2 0 2 t 2 4 6 8 10 12 X(t)

Rysunek 1: Fragmenty funkcji pierwotnych funkcji

PRZYKŁAD

Przykład 1:

Przykład 1:

Dane jest równanie różniczkowe zwyczajne rzędu pierwszego z funkcją niewiadomą :

Powyższe równanie można zapisać w sposób równoważny jako równość różniczek

Jak wiadomo, równość różniczek implikuje równość odpowiednich całek, w danym przypadku równość ta będzie miała postać

Licząc odpowiednie całki otrzymamy

Zatem funkcja , spełniająca RRZ ( 5 ) nie jest zadana jednoznacznie, lecz z dokładnością do dowolnej stałej (stałej całkowania).

Sens geometryczny stałej występującej w powyższym wzorze wynika z interpretacji pochodnej jako tangensa kąta nachylenia do osi prostej stycznej do wykresu funkcji w dowolnym punkcie (zob. Rys. 1). Stąd funkcją pierwotną będzie również każda funkcja postaci , gdzie .

Równania różniczkowe rzędu pierwszego o

Równania różniczkowe rzędu pierwszego o

zmiennych rozdzielonych

zmiennych rozdzielonych

Równanie rzędu pierwszego można na ogół rozwikłać względem zmiennej , przedstawiając go w postaci równoważnej

zwaną postacią kanoniczną RRZ rzędu 1.postacią kanoniczną RRZ rzędu 1. Takiego równania nie można scałkować przy dowolnej prawej stronie. Poniżej

przedstawimy podstawowe typy funkcji, dla których potrafimy podać rozwiązanie bądź to w postaci analitycznej bądź w postaci całek (kwadraturkwadratur).

1. Funkcja nie zależy od zmiennej :

cos t

x(t)

= cos t.

dx = cos t dt ≡ d sin t.

∫ dx = ∫ cos tdt.

x(t) = sin t + C.

x(t)

O X

(t, x(t))

x(t) + C

C = const

F(t, x(t), (t)) = 0

x

_x

_(t)

= φ(t, x),

φ

t

= φ(x).

= dt

(8) Przepisując równanie w postaci , a następnie całkując, otrzymujemy rozwiązanie w postaci uwikłanej:

2. Funkcja nie zależy od zmiennej :

Przepisując równanie w postaci , a następnie całkując, otrzymujemy rozwiązanie w postaci:

3. Równanie typu

Rozwiązanie sprowadza się do warunku

Oznaczenie. Wszystkie równania rozpatrzone w tym punkcie nazywamy RR rzędu 1 o zmiennych rozdzielonych.Wszystkie równania rozpatrzone w tym punkcie nazywamy RR rzędu 1 o zmiennych rozdzielonych.

Równania różniczkowe rzędu pierwszego, które

Równania różniczkowe rzędu pierwszego, które

sprowadzają się do równań o zmiennych

sprowadzają się do równań o zmiennych

rozdzielonych

rozdzielonych

Całkowanie równań różniczkowych (RR) rzędu pierwszego wiąże się, na ogół, z przedstawieniem ich w postaci równań o zmiennych rozdzielonych.

1. Równanie postaci

Stosujemy podstawienie . Różniczkując względem otrzymamy i wówczas wyjściowe równanie ma postać

lub, po rozdzieleniu zmiennych,

Całkując powyższe wyrażenie, otrzymamy

= dt

∫

= t + C, C ∈ R.

φ

x

= ψ(t).

dx = ψ(t) dt

x = ∫ ψ(t)dt + C.

=

.

∫ P(t) dt = ∫ Q(x) dx.

= f(a t + b x).

z = a t + b x

z

t,

z

= a + b

_x

= a + b f(z),

= dt.

∫

= t + C.

(9)

PRZYKŁAD

Przykład 2:

Przykład 2:

W tym przypadku , zaś . Podstawiając to do

powyższego równania, otrzymujemy:

Stąd otrzymujemy rozwiązanie

2. Równania jednorodne. Są to równania, które nie zmieniają kształtu przy transformacjach , gdzie jest dowolną stałą nie równą się zeru. Równanie takie może być sprowadzone do postaci

Stosujemy podstawienie . Wówczas i Otrzymamy wtedy

a po rozdzieleniu zmiennych

Całkując stronami, otrzymamy:

PRZYKŁAD

Przykład 3:

Przykład 3:

Zgodnie z powyższym wzorem , więc mamy do policzenia całkę

Wracając do zmiennej wyjściowej otrzymamy równość

Wprowadzając dogodną stałą zgodnie ze wzorem , po elementarnych przekształceniach otrzymujemy rozwiązanie

3. Do jednorodnego równania sprowadza się równanie postaci

= 2 t + x.

z = 2 t + x

z

= 2 + ,

_x

_{f(z) = z}

∫

= ln

= t.

x = C − 2 (t + 1).

e

x → α x, t → α t

α

= f ( ) .

z =

x = z t

x

= t + z.

z

=

=

,

=

.

log[ ] = ∫

.

= (1 + )

f(z) = z(z + 1)

∫

= ∫

= − .

= − log[ ] ≡ log C − log t.

t x Ct

= log C

C~

x =

.

= f (

) .

(10)

(11)

(12) (13) Rozpatrzmy najpierw przypadek szczególny

Wprowadzamy podstawienie:

Ponieważ więc zatem zmienną będziemy traktować jako nową zmienną niezależną, zaś funkcja będzie nową zmienną zależną. Zauważmy że zachodzą równości oraz . Równanie można zatem przepisać w postaci

gdzie

Przypomnijmy kiedy układ równań liniowych

można rozwiązać względem zmiennych . Postać macierzowa tego układu jest następująca:

Z twierdzenia Cramera wynika, iż układ ma jedno rozwiązanie , o ile

Jeżeli warunek powyższy zachodzi, wówczas możemy w sposób jednoznaczny dobrać stałe w taki sposób że znikną. Dzieląc licznik i mianownik prawej strony równania ( 11 ) przez , otrzymamy wtedy

Jest to jednorodne równanie, które poprzez podstawienie sprowadza się do równania o zmiennych rozdzielonych. Jeżeli , wówczas nie można wyeliminować opisanym wyżej sposobem parametrów . Niemniej jednak ten przypadek również jest całkowalny. Rzeczywiście, równość oznacza, że współczynniki są proporcjonalne, tzn. istnieje stała taka że , . A zatem równanie ( 10 ) można przepisać w postaci równania ( 8 )

I tak jak w równaniu ( 8 ) wprowadzamy podstwienie otrzymując równanie

które jest równaniem o zmiennych rozdzielonych.

Przypadek ogólny, czyli równanie ( 9 ), przekształcamy w podobny sposób: jeżeli , to wówczas przechodzimy do zmiennych , , gdzie stałe

określamy jako rozwiązania układu równań

W wyniku dla funkcji otrzymujemy równanie

=

.

t = r + α,

x = p + β.

x = x(t),

p = p(t),

r

p

dt = dr,

dx = dp

=

,

= α + β + ,

= α + β + .

h

a

b

c

h

a

b

c

{ α + β + = 0,

a

b

c

α + β + = 0

a

b

c

α, β

⋅ ( ) = [

] ⋅ ( ) = − ( ) .

M^

α

β

a

a

,

,

b

b

α

β

c

c

α, β

J = det

M^

=

a

b

−

a

b

≠ 0.

α, β

h

,

h

r

=

= F ( ) .

z =

det M =

a

b

−

a

b

= 0

h

,

h

J = 0

k ≠ 0

a

= k

a

b

= k

b

=

= F( t + x).

a

b

z = t + x,

a

b

= F(z) + ,

b

a

t + x ≠ k( t + x)

a

b

a

b

ξ = t − t

η = x − x

t

,

x

+

+ = 0,

a

t

b

x

c

+

+ = 0.

a

t

b

x

c

η(ξ)

= f (

) = f (

) = F [ ]

(14)

(15) jest to równanie jednorodne.

W przypadku gdy , równanie ( 9 ) można zapisać jako

Podstawienie , sprowadza go do równania o zmiennych rozdzielonych:

UWAGA

Uwaga 1:

Uwaga 1:

W przypadku gdy , równanie ( 9 ) sprowadza się do równania postaci ( 14 ).

4. Równania jednorodne uogólnione. Jest to klasa równań, które się nie zmieniają przy jednoczesnym skalowaniu zmiennej zależnej i niezależnej , gdzie -stałe. Równania takie można przedstawić w postaci

Podstawienie sprowadza równanie ( 15 ) do równania o zmiennych rozdzielonych:

Przykłady równań różniczkowych wykorzystywanych

Przykłady równań różniczkowych wykorzystywanych

w naukach przyrodniczych

w naukach przyrodniczych

= f (

) = f (

) = F [ ]

t + x = k( t + x)

a

b

a

b

= f (

) = ( t + x).

f

a

b

z = t + x

a

b

=

(z) + = F(z).

b

f

a

t + x = k( t + x)

a

b

a

b

t → α t, x →

α

x

_{0 ≠ α, k}

=

f ( ) .

t

z = xt

=

.

(16) (17) (18) (19)

PRZYKŁAD

Przykład 4:

Przykład 4:

Model maltuzjański. W biologii ważnym problemem jest określenie dynamiki populacji bakterii.

Otóż: niech oznacza liczebność populacji w chwili czasu . W sytuacji, gdy zasoby pokarmowe są nieograniczone, liczebność populacji w chwili w dobrym przybliżeniu opisuje wzór

gdzie jest stałą. Równość tę można przedstawić w postaci

Dokonując w powyższym równaniu przejścia granicznego

otrzymujemy równanie różniczkowe

zwane modelem maltuzjańskim dynamiki populacji.modelem maltuzjańskim dynamiki populacji. Równanie to można przedstawić w postaci równości różniczek

dla Całkując wyrażenie

(ponownie wykorzystujemy to iż równość różniczek implikuje 1 _{równość odpowiednich całek), otrzymamy równość}

gdzie . Kładąc mamy

Jednakże spełnia równanie ( 18 ), więc spełnia równanie ( 17 ) przy dowolnej stałej

Faktycznie uzyskaliśmy nieskończenie wiele rozwiązań naszego problemu. Są one wyznaczone poprzez dobór dowolnej stałej (zgodnie z sensem biologicznym rozwiązania, ). Całość rozwiązań można przedstawić na płaszczyźnie ( ), zwanej płaszczyzną fazowąpłaszczyzną fazową (zob. Rys. 2). W jaki sposób można interpretować wzór ( 18 )? Ewolucja populacji będzie zależeć od tego, jaka była liczebność populacji w chwili początkowej .

Zadając wielkość pozbywamy się niejednoznaczności, gdyż wykorzystując warunek

otrzymamy wzór

który już jednoznacznie określa ewolucję takiej populacji, która w chwili liczyła bakterii

2

P(t) ≥ 0

t

t + Δt

P(t + Δt) = P(t) + kP(t) Δ t,

k

= kP(t).

=

,

lim

= kP(t),

= d(log |P|) = kdt = d(kt) .

P ≠ 0.

d(log(P)) = d(kt)

log |P| = kt + ,

C~

∈ R

C~

C~

= log C, C > 0

P = C

e

.

P = 0

C ∈ R.

C

C ≥ 0

t, x

t

P( ) =

t

P

P( ) =

t

P

= C

e

,

P(t) =

P

e

,

t

P

t x

(20) (21) (22)

PRZYKŁAD

Przykład 5:

Przykład 5:

Dynamika punktu materialnego.

Dynamika punktu materialnego. Innym prostym przykładem jest równanie dynamiki punktu materialnego o masie . Drugie prawo Newtona daje następujący znany związek pomiędzy masą , siłą a przyspieszeniem :

W przypadku jednowymiarowym wszystkie trzy wielkości są wielkościami skalarnymi. Oznaczamy je wówczas przez Jeżeli założymy że to dostaniemy, po podzieleniu przez , równanie

. Jak wiadomo, przyspieszenie określa szybkość zmiany prędkości punktu materialnego w chwili , a jego precyzyjna definicja jest następująca:

Z kolei, prędkość określa się jako szybkość zmiany położenia przestrzennego punktu materialnego:

Daje to zatem równanie

czyli Mamy więc w tym przypadku do czynienia z równaniem różniczkowym zwyczajnym rzędu drugiego.

Równanie to całkuje się w dwóch krokach. Pierwszym krokiem jest całkowanie równania , które jest równoważne

równaniu . Całkując je otrzymamy

gdzie jest dowolną stałą całkowania.

Na drugim kroku wykorzystujemy to że z ( 21 ), wynika równość różniczek , która z kolei implikuje równość całek

gdzie są dowolnymi stałymi. Zatem ruch jednowymiarowy punktu materialnego w przypadku braku sił ( ) określa się wzorem

Ważnym wnioskiem wynikającym z powyższego przykładu jest, że przy znajdowaniu rozwiązania równania , które jest najprostszym skalarnym równania różniczkowego zwyczajnego rzędu 2, musieliśmy dwa razy zastosować procedurę całkowania i stąd w rozwiązaniu

( 22 ) pojawiły się dwie dowolne stałe. Należy więc założyć, iż w przypadku równania -go rzędu

znalezienie rozwiązania będzie wymagać -krotnego całkowania, a to z kolei wyprodukuje nam dowolnych stałych. Domniemanie to jest jak najbardziej słuszne: prawdziwe jest następujące twierdzenie.

m

m

F⃗

a⃗

m = .

a⃗ F⃗

m, F, a.

F = 0,

m ≠ 0

a = 0

v

t

a(t) =

lim

=

= (t).

v

v(t)

x(t)

v(t) =

lim

=

= (t).

x

a = v(t) =

=

= 0,

= 0.

= 0

dv = 0 ∗ dt = 0

v(t) =

= ,

C

C

dx = d( t)

C

∫ dx = x = ∫ d( t) =

C

C

+

C

t,

,

C

C

F = 0

x(t) =

C

+

C

t,

,

∈ R.

C

C

d x(t)/d = 0

_t

n

n

n

(23)

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1:

Rozwiązanie ogólneogólne skalarnego równania różniczkowego zwyczajnego rzędu zależy

od dowolnych stałych (tzw. stałych całkowania). Stałych całkowania jest dokładnie tyle, ile wynosi rząd równania. Wróćmy teraz do rozwiązania ( 22 ), równania ( 21 ) i zadajmy sobie pytanie odnośnie jego praktycznego

wykorzystania w celu przewidywania położenia punktu materialnego w ruchu jednostajnym prostoliniowym. Otóż, żeby wyeliminować nieoznaczoności tkwiące w tym

równaniu w postaci dowolności stałych całkowania, musimy dodatkowo znać zarówno położenie , w którym znajdował się punkt materialny w chwili początkowej , jak i prędkość , z jaką punkt się

porusza. Daje to układ równań algebraicznych

z którego możemy łatwo określić stałe :

A zatem położenie w czasie punktu materialnego spełniającego zadane warunki początkowe

jest jednoznacznie określone wzorem

Przypisy

Przypisy

1. Teza ta jest poprawna tylko wówczas gdy po różne strony równości stoją funkcje tylko jednego argumentu, innymi słowami, zmienne się nie mieszają

2. Rozwiązanie ( 19 ) mówi nam, iż populacja bakterii rośnie z czasem w sposób wykładniczy. Prowadzi to do

wiadomego paradoksu: w skończonym czasie niewielka populacja bakterii rozrasta się do tego stopnia, iż pokrywa metrową warstwą kulę ziemską. Jest to związane

z założeniem o nieograniczonej bazie pokarmowej oraz braku czynników powodujących kurczenie się populacji. Oba te założenia nie są prawdziwe, niemniej jednak

równanie ( 17 ) jest użyteczne, gdyż opisuje poprawnie początkowe stadium rozwoju populacji, w którym 'walka' o pokarm oraz inne

czynniki powodujące spowolnienie wzrostu nie są jeszcze istotne. Bardziej realistycznym modelem uwzględniającym powyższe czynniki naturalnego spowolnienia

jest równanie postaci

zwane równaniem logistycznym.równaniem logistycznym.

Zagadnienie początkowe (zagadnienie Cauchy'ego).

Zagadnienie początkowe (zagadnienie Cauchy'ego).

Poprawność zadania warunków początkowych

Poprawność zadania warunków początkowych

n

n

x

t

v

x( ) =

t

C

+

C

t

= ,

x

x

( ) =

t

C

= ,

v

,

C

C

=

−

,

= .

C

x

v

t

C

v

t

x( ) = ,

t

x

x

( ) =

t

v

x(t) =

x

+ (t − ).

v

t

= k P(t) (1 −

) = 0,

(24)

(25) Powstaje pytanie: co należy zrobić, by rozwiązanie skalarnego RRZ nie zależało od dowolnych stałych? W innym sformułowaniu pytanie to brzmi następująco: przy jakich warunkach rozwiązanie RRZ będzie jednoznaczne? Otóż, skoro rozwiązanie ogólne skalarnego RRZ -go rzędu zależy od dowolnych stałych, to, żeby otrzymać rozwiązanie jednoznaczne, wystarczy, jak się wydaje, podać dodatkowych warunków algebraicznych. Domniemanie to jest słuszne w większości przypadków, z którymi stykamy się w praktyce.

Jednak w pewnych wyjątkowych sytuacjach, a mianowicie wówczas, gdy dane początkowe są zadane niepoprawnie, rozwiązanie wciąż będzie niejednoznaczne. Może też powstać sytuacja, że przy źle postawionych danych początkowych rozwiązanie nie będzie w ogóle istnieć.

Dla przykładu rozpatrzmy następujące równanie:

Równanie to można przepisać w postaci równości

które ma równowazną postać różniczkową

Implikuje to następujący ciąg równości:

Podstawiając funkcję do równania wyjściowego, możemy przekonać się, że czyni ona z niego tożsamość. Lewa strona:

Prawa strona:

Zatem

zadając warunek początkowy w postaci

i rozwiązując równanie algebraiczne względem , otrzymamy jedyne rozwiązanie Zadając warunek początkowy

otrzymamy niedorzeczność: Przyczyną tego jest nieokreśloność prawej strony równania przy . Warunek początkowy

jest spełniony przy dowolnej wartości stałej .Przyczynę tego można zrozumieć, gdy rozpatrzymy zbiór wszystkich możliwych rozwiązań równania ( 24 ) postaci ( 25 ). Obrazuje go na płaszczyźnie fazowej pęk linii prostych przechodzących przez początek współrzędnych, (zob. Rys. 3). Widzimy że początek współrzędnych jest jedynym punktem na płaszczyźnie, przez który przechodzą wszystkie rozwiązania równania. Dlatego właśnie zadanie warunków początkowych w tym punkcie prowadzi do nieijednoznaczności.

n

n

n

= .

= ,

dlog x = dlog t.

∫ dlog x = ∫ dlog t ⇔ log x = log t + log C ⇔ x = Ct, C ∈ R.

x = C t

= C,

=

= C.

x( ) = a, gdzie

t

t

≠ 0,

x( ) = a = C

t

t

C

x(t) = a .

x(0) = b ≠ 0,

b = C ⋅ 0.

t = 0

x(0) = 0,

C

(t, x)

(26) - 3 - 2 - 1 1 2 3 t - 10 - 5 5 10 f(t) -> x x

Rysunek 3: Graficzna reprezentacja zbioru rozwiązań równania ( 24 ) odpowiadających różnym wartościom parametru , na płaszczyźnie fazowej

Podsumowując to co powiedzieliśmy, wprowadzimy następujące oznaczenie: Punkt Punkt płaszczyzny fazowej nazywa się płaszczyzny fazowej nazywa się punktem osobliwym, jeżeli w tym punkcie prawa strona RRZ

punktem osobliwym, jeżeli w tym punkcie prawa strona RRZ

przybiera wartość zerową, lub jest nieoznaczona.

przybiera wartość zerową, lub jest nieoznaczona. Ogólna reguła więc brzmi następująco:

Postawienie warunków początkowych w punkcie osobliwym prowadzi do niejednoznaczności rozwiązania zagadnienia Postawienie warunków początkowych w punkcie osobliwym prowadzi do niejednoznaczności rozwiązania zagadnienia początkowego, lub do niedorzeczności.

początkowego, lub do niedorzeczności.

Liniowe równania różniczkowe rzędu pierwszego

Liniowe równania różniczkowe rzędu pierwszego

gdzie - wiadome funkcje, przy czym zakładamy że nie równa się tożsamosciowo zeru. Stowarzyszonym równaniem jednorodnym nazywamy równanie postaci

Po przemnożeniu tego równania przez otrzymujemy równanie o zmiennych rozdzielonych:

Stąd, po stałkowaniu otrzymjemy

Rozwiązanie problemu niejednorodnego uzyskujemy metodą uzmienniania stałejmetodą uzmienniania stałej. Polega ona na zamianie stałej w powyższeym wzorze przez pewną nieznaną funkcję .

Rozwiązanie poszukujemy w postaci , . Po

podstawieniu do równania wyjściowego otrzymamy:

Zatem . Stąd już łatwo można otrzymać postać rozwiązania ogólnego problemu niejednorodnego:

C (t, x)

( , )

t

x

= f(t, x)

+ p(t) x(t) = q(t),

p(t), q(t)

q(t)

+ p(t) (t) = 0.

x

= −p(t) dt.

= C

,

C ∈ R.

x

e

C

C(t)

x(t) = C(t) e

_{F(t) = ∫ p(t) dt}

= q(t)

lub dC = q(t)

dt.

e

e

C(t) =

C

+ ∫ q(t)

e

dt

x(t) =

e

( + ∫ q(t)

_C

_e

dt) , F(t) = ∫ p(t) dt.

(27) (28) (29) (30) (31) (32)

PRZYKŁAD

Przykład 6:

Przykład 6:

Z postaci równania odczytujemy że , natomiast . Do policzenia mamy całkę

oraz całkę

Rozwiązanie Rozwiązanie

Rozwiązanie ogólne równania ( 27 ) ma postać

Metoda Eulera

Metoda Eulera

Omówiliśmy , których rozwiązania można uzyskać za pomocą procesu całkowania. Niestety, nawet jeśli ograniczymy się do RRZ rzędu pierwszego, to większości z nich nie jesteśmy w stanie rozwiązać poprzez ich całkowanie, co więcej, rozwiązania takich równań nie są funkcjami elementarnymi. Dlatego powinniśmy w dalszym ciągu omówić bardziej uniwersalne metody.

Rozpatrzmy parę , gdzie jest zmienną niezależną, natomiast jest pewną różniczkowalną funkcją zmiennej Zadamy sobie pytanie, co oznacza równość

Odpowiedź, którą już znamy, brzmi następująco: prawa strona równania zadaje w każdym punkcie płaszczyzny fazowej wielkość pochodnej rozwiąznia przechodzącego przez ten punkt. Można to przeformułować jeszcze w taki sposób: prosta

jest styczna do rozwiązania równania ( 28 ) spełniającego warunek początkowy Rozwinięcie tego rozwiązania w szereg Taylora

pozwala wnioskować że "dokładne" rozwiązanie w małym otoczeniu punktu różni się od linii prostej ( 29 ), o wyraz który jest rzędu . A więc, dokładne rozwiązanie można przybliżać odcinkami prostej postaci

gdzie - zbiór punktów leżących w pobliżu poszukiwanej krzywej. W poszukiwaniu takiego przybliżenia korzystamy z pojęcia pola kierunków, które można określić jako pole taz zwanych infinitezymalnychinfinitezymalnych odcinków zadanych w każdym punkcie za pomocą wzoru

Obraz graficzny takiego pola kierunków można uzyskać w każdym z dostępnych pakietów matematyki komputerowej ( MathCad,MathCad, MathLab, Maple, Mathematica

MathLab, Maple, Mathematica ). Tutaj i dalej będziemy przytaczać "orfografię" pakietu MathematicaMathematica. Zobrazujemy, dla przykładu, pole kierunków funkcji

Komórka 1.1.

+ x(t) = t

p(t) = 1

q(t) = t

F(t) = ∫ p(t) dt ≡ ∫ dt = t.

∫

e

q(t) dt = ∫ t dt = (t − 1).

_e

_e

x(t) =

e

( + (t − 1)).

_C

_e

x, y

x

y

x.

= f(x, y).

y

( , )

x

y

y = ϕ(x; C)

y = (x − ) f( , ) +

x

x

y

y

y = ϕ(x; C)

y( ) = .

x

y

y(x) = + (x − ) f( , ) + O(|x −

y

x

x

y

x

|

)

x

|x − x

|

= (x − ) f( , ) +

y

x

x

y

y

( , ), k = 0, 1, . . . .

x

y

(x, y)

(dx, dy) = dx (1, f(x, y)) .

f(x, y) = x − y.

(33)

(34) Wynikiem jest wykres pola kierunków przedstawiony na Rys. 4

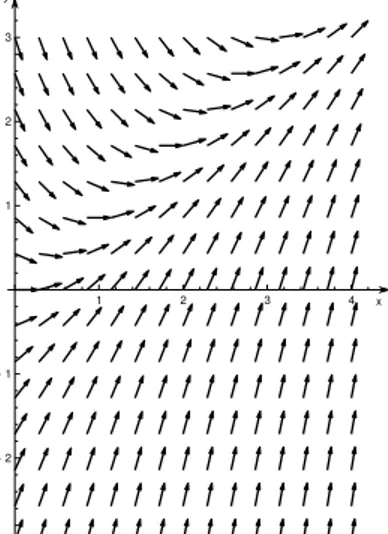
1 2 3 4 x - 3 - 2 - 1 1 2 3 y

Rysunek 4: Graficzna reprezentacja pola kierunków funkcji

Na Rys. 5 przedstawione zostało pole kierunków z kilkoma rozwiązaniami dokładnymi równania

które dane są wzorem

Widać na nim wyraźnie, że pole kierunków jest styczne do rozwiązania w każdym punkcie.

1 2 3 4 x - 3 - 2 - 1 1 2 3 y

Rysunek 5: Graficzna reprezentacja pola kierunków funkcji oraz rozwiązania dokładne (6) odpowiadające stałym całkowania , oraz

Znajomość pola kierunków w celu konstrukcji przybliżonego rozwiązania równania różniczkowego wykorzystał po raz pierwszy Leonard Euler. Jego algorytm dotyczy poszukiwania rozwiązania przybliżonego zadadnienia Cauchyego

Traktując stałe oraz funkcję jako znane wielkości, Euler zaproponował opis łamanej przybliżającej rozwiązanie na odcinku w postaci następującego algorytmu:

In[1] := [V ector FieldPlot ]

s

f[ , ] = x − y;

x

y

V F1 = V ectorFieldPlot[{1, f[x, y]}, {x, 0, 4}, {y, −3, 3},

Axes → True, ScaleFunction → (1&), AxesLabel → {x, y}]

f(x, y) = x − y

= x − y,

y

y =

C

e

+ x − 1.

= f(x, y),

y( ) = .

y

_x

_y

,

x

y

f(x, y)

[a = , b]

x

= + h f( , ),

(35)

gdzie .

Do tego, by przybliżenie dostatecznie dobrze opisywało poszukiwane rozwiązanie, należy stosować dostatecznie mały krok (czyli duże ). Do zastosowania powyższego algorytmu, w zasadzie, wystarczy umieć posługiwać się kalkulatorem, jednak odpowiednie obliczenia są bardzo żmudne. Podamy, zgodnie z 3_,

dwie wersje algorytmu Eulera, zaimplentowane w pakiecie MathematicaMathematica dla rozwiązywania zagadnienia początkowego

na odcinku z krokiem . Prosty kod wygląda następująco: Komórka 1.2.

UWAGA

Uwaga 2:

Uwaga 2:

Warunki są potrzebne by uniknąć nieskończonej rekursji, która mogłaby powstać, jeżeli pozwolilibyśmy przybierać dowolne (w tym również ujemne) wartości.

Jeżeli teraz dodać moduł Komórka 1.3.

to otrzymamy poszukiwane przybliżone rozwiązanie w postaci tabelki.

Powyższy algorytm przy dużej liczbie iteracji będzie pracować wolno, ponieważ przy każdej kolejnej liczbie obliczenia rozpoczynają się od punktu . Algorytm można jednak zmodyfikować w taki sposób że wielkości będą zapamiętywane, co znacznie usprawni obliczenia. Kolejną rzeczą jest zastąpienie tabelki przez funkcję interpolacyjną

. Wszystko to razem wzięte tworzy następujący szybko działający algorytm: Komórka 1.4.

= + h f( , ),

y

y

x

y

= + h f( , ),

y

y

x

y

= + h f( , ),

y

y

x

y

. . . .

= + h f( , ),

y

y

x

y

. . . .

=

+ h f(

,

),

y

y

x

y

h =

h

N

= x − y, y( ) = 0.

y

_x

(0, 4)

h = 0.2

x[ ] := nh;

n

y[ ] := y[n − 1] + hf[x[n − 1], y[n − 1]]/; n > 0&&n ∈ Integers;

n

h = 0.2;

y0 = 0;

f[ , ] = x − y;

x

y

n > 0 n ∈ Integers

n

sol = Table[{x[n], y[n]}, {n, 0, 4/h}],

N

n

y[0]

v[0], v[1], . . . v[n]

sol

vEul[ ] = Interpolation[sol][t]

t

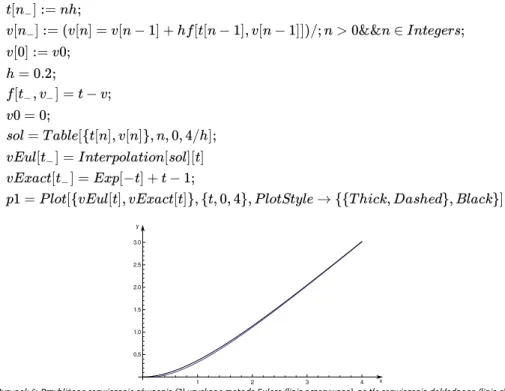
(36) 1 2 3 4 0.5 1.0 1.5 2.0 2.5 3.0 y x

Rysunek 6: Przybliżone rozwiązanie równania (2) uzyskane metodą Eulera (linia przerywana), na tle rozwiązania dokładnego (linia ciągła)

W wyniku implementacji tego algorytmu uzyskujemy rozwiązanie przybliżone na tle rozwiązania dokładnego, co ilustruje Rys. 6.

Przypisy

Przypisy

1. Teza ta jest poprawna tylko wówczas gdy po różne strony równości stoją funkcje tylko jednego argumentu, innymi słowami, zmienne się nie mieszają

2. Rozwiązanie ( 19 ) mówi nam, iż populacja bakterii rośnie z czasem w sposób wykładniczy. Prowadzi to do

wiadomego paradoksu: w skończonym czasie niewielka populacja bakterii rozrasta się do tego stopnia, iż pokrywa metrową warstwą kulę ziemską. Jest to związane

z założeniem o nieograniczonej bazie pokarmowej oraz braku czynników powodujących kurczenie się populacji. Oba te założenia nie są prawdziwe, niemniej jednak

równanie ( 17 ) jest użyteczne, gdyż opisuje poprawnie początkowe stadium rozwoju populacji, w którym 'walka' o pokarm oraz inne

czynniki powodujące spowolnienie wzrostu nie są jeszcze istotne. Bardziej realistycznym modelem uwzględniającym powyższe czynniki naturalnego spowolnienia

jest równanie postaci

zwane równaniem logistycznym.równaniem logistycznym.

3. D. Dubin, Numerical and Analytical Methods for Scientists and Enginneers Using Mathematica, John Wiley and Sons, New Jersey, 2003

Równania różniczkowe liniowe wyższych rzędów

Równania różniczkowe liniowe wyższych rzędów

-podstawowe pojęcia

podstawowe pojęcia

t[ ] := nh;

n

v[ ] := (v[n] = v[n − 1] + hf[t[n − 1], v[n − 1]])/; n > 0&&n ∈ Integers;

n

v[0] := v0;

h = 0.2;

f[ , ] = t − v;

t

v

v0 = 0;

sol = Table[{t[n], v[n]}, n, 0, 4/h];

vEul[ ] = Interpolation[sol][t]

t

vExact[ ] = Exp[−t] + t − 1;

t

p1 = Plot[{vEul[t], vExact[t]}, {t, 0, 4}, PlotStyle → {{Thick, Dashed}, Black}]

= k P(t) (1 −

) = 0,

dP(t)

(37)

(38)

DEFINICJA

Definicja 2: Równania liniowego rzędu n-tego

Definicja 2: Równania liniowego rzędu n-tego

Równaniem różniczkowym liniowym rzędu nazywamy równanie postaci

gdzie jest szukaną funkcją a dane funkcje i są ciągłe i określone w

przedziale o wartościach rzeczywistych. Przez przedział rozumiemy jeden z następujących zbiorów: lub .

UWAGA

Uwaga 3:

Uwaga 3:

Jeżeli dla każdego to równanie ( 37 ) będziemy nazywać równaniem jednorodnymrównaniem jednorodnym, w przeciwnym razie równaniem niejednorodnym równaniem niejednorodnym.

DEFINICJA

Definicja 3: Rozwiązania

Definicja 3: Rozwiązania

Rozwiązaniem równania ( 37 ) nazywamy funkcję określoną w przedziale i -krotnie różniczkowalną, spełniającą dla każdego równanie ( 37 ).

DEFINICJA

Definicja 4: Problemu początkowego

Definicja 4: Problemu początkowego

Zagadnienie polegające na znalezieniu rozwiązania równania ( 37 ), które dla ustalonego spełnia -równości:

gdzie są danymi stałymi, będziemy nazywać problemem początkowymproblemem początkowym.

n

(t)

(t) +

(t)

(t) + ⋯ + (t) (t) + (t)y(t) = f(t)

a

y

a

y

a

y

a

y(t)

y : I → R,

f(t)

a

(t), i = 0, …, n

I ⊂ R

I

(a, b), (−∞, a), (a, +∞)

R

f(t) = 0

t ∈ I,

y(t)

I n

t ∈ I

∈ I

t

n

y( ) = ,

t

b

y

( ) = , …,

t

b

y

( ) =

t

b

,

, …,

b

b

PRZYKŁAD

Przykład 7:

Przykład 7:

Pokażemy, że funkcja jest rozwiązaniem problemu początkowego postaci

Rozwiązanie: i więc czyli

funkcja jest rozwiązaniem równania.

Ponadto i , zatem funkcja spełnia waruneki początkowe.

PRZYKŁAD

Przykład 8:

Przykład 8:

Pokażemy, że funkcja jest rozwiązaniem następującego problemu początkowego

w przedziale dla dowolnego parametru .

Rozwiązanie: i zatem

Ponadto i , co kończy dowód, że jest rozwiązaniem problemu początkowego.

y(t) = sin(2t)

(t) + 4y(t) = 0, y(0) = 0, (0) = 2, gdzie t ∈ R.

y

_y

(t) = 2 cos(2t)

y

_y

_{(t) = −4 sin(2t),}

_y

_{(t) + 4y(t) = −4 sin(2t) + 4 sin(2t) = 0,}

y(t)

y(0) = sin(0) = 0

y

(0) = 2 cos(0) = 2

_y(t)

y(t) = c + t + 1

t

(t) − 2t (t) + 2y(t) = 2, y(0) = 1,

(0) = 1

t

_y

_y

_y

(−∞, ∞),

c

(t) = 2ct + 1

y

_y

_{(t) = 2c}

(t) − 2t (t) + 2y(t) = 2c − 2t(2ct + 1) + 2(c + t + 1) = 2.

t

_y

_y

_t

_t

y(0) = 1

y

(0) = 1

_y(t)

(39) (40)

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2:

Niech funkcje będą rozwiązanimi równania jednorodnego

TEZA: TEZA:

Wtedy dowolna liniowa kombinacja tych funkcji gdzie

są dowolnymi stałymi, jest również rozwiązaniem równania ( 39 )

DOWÓD: DOWÓD:

Dowód przeprowadzimy w przypadku, gdy , (dla dowolnego dowód jest analogiczny). Niech będą rozwiązaniami równania

Definiujemy gdzie są to dowolne stałe, wtedy

Podstawiając teraz do równania ( 40 ) otrzymujemy

Zatem jest rozwiązaniem równania ( 40 ).

PRZYKŁAD

Przykład 9:

Przykład 9:

Funkcje i są rozwiązaniami równania

Zatem na mocy twierdzenia 2, funkcja gdzie - są to dowolne stałe, jest też rozwiązaniem tego równania.

(t), …, (t)

y

y

(t)

(t) +

(t)

(t) + ⋯ + (t) (t) + (t)y(t) = 0.

a

y

a

y

a

y

a

y(t) =

c

y

(t) + ⋯ +

c

y

(t),

, …

c

c

k = n = 2

k, n ∈ N

(t), (t)

y

y

(t) (t) + (t) (t) + (t)y(t) = 0.

a

y

a

y

a

y(t) =

c

y

(t) +

c

y

(t)

c

,

c

(t) =

(t) +

(t) i

(t) =

(t) +

(t).

y

_c

_y

c

y

y

c

y

c

y

y(t), (t),

y

_y

(t)

(t) (

(t) +

(t)) + (t) (

(t) +

(t)) + (t) (

(t) +

(t)]) =

a

c

y

c

y

a

c

y

c

y

a

c

y

c

y

( (t) (t) + (t) (t) + (t) (t)) + ( (t) (t) + (t) (t) + (t) (t)]) = 0.

c

a

y

a

y

a

y

c

a

y

a

y

a

y

y(t)

(t) =

y

e

y

(t) =

e

y

+ 3 + 2y = 0.

y

y(t) =

c

e

+

c

e

,

c

,

c

TWIERDZENIE

Twierdzenie 3:

Twierdzenie 3: O istnieniu i jednoznaczności rozwiązania problemu Cauchy'ego

O istnieniu i jednoznaczności rozwiązania problemu Cauchy'ego

ZAŁOŻENIA: ZAŁOŻENIA:

Niech funkcje i będą ciągłe i określone w przedziale ponadto dla

każdego

TEZA: TEZA:

Wtedy problem początkowy

gdzie , zaś - są to dowolne stałe, posiada dokładnie jedno rozwiązanie określone w przedziale .

Dowód tego twierdzenia jest przedstawiony w module Twierdzenia o istnieniu i jednoznaczności dla równań różniczkowych zwyczajnych.

Liniowa zależność i niezależność funkcji

Liniowa zależność i niezależność funkcji

DEFINICJA

Definicja 5: Liniowej zależności zbioru funkcji

Definicja 5: Liniowej zależności zbioru funkcji

Mówimy, że zbiór funkcji zbiór funkcji określonych na przedziale jest liniowo zależnyliniowo zależny, jeżeli istnieją stałe

nie wszystkie równe zero, takie że dla każdego .

DEFINICJA

Definicja 6: Liniowej niezależności zbioru funkcji

Definicja 6: Liniowej niezależności zbioru funkcji

Mówimy, że zbiór funkcjizbiór funkcji określonych na przedziale jest liniowo niezależny liniowo niezależny jeśli nie jest liniowo zależny. Inaczej mówiąc, równość zachodzi dla każdego jedynie w przypadku, gdy wszystkie współczynniki są równe zero.

f(t)

a

(t), gdzie k = 0, …, n,

I ⊂ R ,

a

(t) ≠ 0,

t ∈ I.

{ (t)

a

y

(t) +

a

(t)

y

(t) + ⋯ + (t) (t) + (t)y(t) = f(t),

a

y

a

y( ) = , ( ) = , …,

t

b

y

t

b

y

( ) =

t

b

t ∈ I,

∈ I

t

b

, . . . ,

b

I

(t), …, (t)

f

f

I ⊂ R

, …,

c

c

c

f

(t) + ⋯ +

c

f

(t) = 0 ,

t ∈ I

(t), …, (t)

f

f

I

(t) + ⋯ +

(t) = 0

c

f

c

f

t ∈ I

, i = 1, …, n

c

(41)

UWAGA

Uwaga 4:

Uwaga 4:

Z liniowej zależności funkcji wynika, że jedną z nich można przedstawić jako kombinację pozostałych. Na przykład: jeśli to

Stąd wynika, że dwie funkcje i są liniowo zależne wtedy i tylko wtedy, gdy istnieje stała taka, że .

PRZYKŁAD

Przykład 10:

Przykład 10:

Funkcje określone na są liniowo zależne.

Istotnie jeśli weżmiemy to otrzymamy tożsamość

co oznacza, że funkcje są liniowo zależne.

PRZYKŁAD

Przykład 11:

Przykład 11:

Pokażemy, że funkcje są liniowo niezależne.

Należy zatem pokazać, że następująca tożsamość

zachodzi jedynie w przypadku gdy .

Z równości Liniowa zależnośc i niezależność funkcji-( 1 ) dla wynika, że . Uwzględniając, że i podstawiając do równości Liniowa zależnośc i niezależność funkcji-( 1 ) za kolejno i otrzymujemy następujący układ równań

którego jedynym rozwiązaniem jest i co kończy dowód liniowej niezależności.

(t), …, (t)

f

f

≠ 0,

c

(t) = −

(t) −

(t) − ⋯ −

(t).

f

f

f

f

f(t) g(t)

c

f(t) = cg(t)

(t) = t, (t) = , (t) = 4t − 3

f

f

t

f

t

R

= −4,

= 3,

= 1,

c

c

c

−4 (t) + 3 (t) + (t) = −4t + 3 + 4t − 3 = 0

f

f

f

t

t

(t), (t), (t)

f

f

f

(t) = 1, (t) = t, (t) =

f

f

f

t

(t) +

(t) +

(t) = 0 dla t ∈ R

c

f

c

f

c

f

= = = 0

c

c

c

t = 0,

c

= 0

c

= 0

t

−1 1,

{ − + = 0

c

c

+ = 0,

c

c

= 0

c

c

= 0,

(42) (43) (44)

TWIERDZENIE

Twierdzenie 4:

Twierdzenie 4:

Zakładamy, że funkcje określone na przedziale są krotnie różniczkowalne i wyznacznik

nie jest równy zero przynajmniej dla jednego z przedziału .

TEZA: TEZA:

Wtedy funkcje są liniowo niezależne. Powyższy wyznacznik będziemy oznaczać i

nazywać WrońskianemWrońskianem, inaczej wyznacznikiem macierzy Wrońskiegowyznacznikiem macierzy Wrońskiego.

DOWÓD: DOWÓD:

Dowód twierdzenia podamy w przypadku, gdy Dla większych dowód jest podobny. Zakładamy, że istnieje dla którego

Dla dowodu nie wprost zakładamy, że funkcje i są liniowo zależne. To oznacza, że istnieją stałe jednocześnie nie równe zero takie, że dla każdego zachodzi równość

Różniczkując stronami równość Liniowa zależnośc i niezależność funkcji-( 3 ) dostajemy

Dla z równości Liniowa zależnośc i niezależność funkcji-( 3 ) i Liniowa zależnośc i niezależność funkcji-( 4 ) otrzymujemy układ równań

o niewiadomych i dla którego wyznacznik

Zatem układ ten posiada jedynie rozwiązanie zerowe i co jest sprzeczne z założeniem, że i nie są jednocześnie równe zero.

Oznacza to, że funkcje i są liniowo niezależne.

WNIOSEK

Wniosek 1:

Wniosek 1:

Jeżeli funkcje są - krotnie różniczkowalne na i są liniowo zależne, to dla każdego

(t), …, (t)

f

f

I ⊂ R

n − 1

∣

∣

∣

∣

∣

∣

∣

(t)

f

(t)

f

⋮

(t)

f

(t)

f

(t)

f

⋮

(t)

f

…

…

⋱

…

(t)

f

(t)

f

⋮

(t)

f

∣

∣

∣

∣

∣

∣

∣

t

I

(t), …, (t)

f

f

W( (t), …, (t))

f

f

n = 2.

n

∈ I,

t

W( ( ), ( )) ≠ 0.

f

t

f

t

(t)

f

f

(t)

c

,

c

t ∈ I

(t) +

(t) = 0.

c

f

c

f

(t) +

(t) = 0.

c

f

c

f

t = ,

t

{

c

f

( ) +

t

c

f

( ) = 0

t

( ) +

( ) = 0

c

f

t

c

f

t

c

c

,

W( ( ), ( )) ≠ 0.

f

t

f

t

= 0

c

c

= 0,

c

c

(t)

f

f

(t)

(t), …, (t)

f

f

n − 1

I

W( (t), …, (t)) = 0,

f

f

t ∈ I.

UWAGA

Uwaga 5:

Uwaga 5:

Z tego, że wrońskian dla funkcji jest równy zero dla każdego nie wynika, że funkcje są liniowo zależne. Na przykład: funkcje są różniczkowalne w i

dla każdego . Funkcje te są liniowo niezależne, ponieważ nie istnieje takie, że dla każdego .

PRZYKŁAD

Przykład 12:

Przykład 12:

Pokażemy, że funkcje i są liniowo niezależne. W tym celu obliczamy ich wrońskian

Stąd, na mocy twierdzenia Liniowa zależnośc i niezależność funkcji-1, funkcje i są liniowo niezależne.

PRZYKŁAD

Przykład 13:

Przykład 13:

Pokażemy, że funkcje są liniowo zależne.

Ponieważ zatem

dla każdego .

Ponieważ współczynniki przy nie są równe zero, więc funkcje są liniowo

zależne.

(t), …, (t)

f

f

t ∈ I

(t), …, (t)

f

f

f

(t) = , (t) = t|t|

t

f

R

W( (t), (t)) = 0,

f

f

t ∈ R

c ∈ R

(t) = c (t),

f

f

t ∈ R

(t) = , (t) = t

f

e

f

e

f

(t) =

e

W( (t), (t), (t)) =

f

f

f

=

=

∣

∣

∣

∣

∣

e

2e

4e

te

(2t + 1)e

(4t + 4)e

e

e

e

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

e

e

3e

te

(t + 1)e

(3t + 4)e

e

0

0

∣

∣

∣

∣

∣

⋅

= [ (3t + 4) − (3t + 3) ] =

≠ 0.

e

∣

∣

∣

_3e

e

_{(3t + 4)e}

(t + 1)e

∣

∣

∣ e

_e

_e

_e

(t) = , (t) = t

f

e

f

e

f

(t) =

e

(t) = sin t, (t) = cos t, (t) = sin(t + )

f

f

f

(t) = sin(t + ) = sin tcos + cos tsin =

sin t + cos t =

(t) +

(t),

f

f

f

(t) +

(t) − (t) = 0

f

f

f

t ∈ R

(t), (t), (t)

f

f

f

f

(t), (t), (t)

f

f

PRZYKŁAD

Przykład 14:

Przykład 14:

Pokażemy, że dla dowolnego funkcje są liniowo niezależne. I-sposób:

I-sposób:

Należy pokazać prawdziwość następującej implikacji:

Wynika ona bezpośrednio z faktu, że wielomian niezerowy o współczynnikach rzeczywistych stopnia ma co najwyżej różnych pierwiastków rzeczywistych. Ponieważ wielomian ma nieskończenie wiele pierwiastków więc musi być wielomianem zerowym, czyli wszystkie jego wspóczynniki są równe zero.

II-sposób: II-sposób:

Ponieważ wrońskian funkcji :

jest różny od zera, więc liniowa niezależność funkcji wynika z twierdzenia Liniowa zależnośc i niezależność funkcji-1.

WNIOSEK

Wniosek 2:

Wniosek 2:

Z przykładu Liniowa zależnośc i niezależność funkcji-5 wynika, że funkcje są liniowo niezależne.

n

1, t, , …,

t

_t

1 + t + ⋯ +

= 0, t ∈ R ⟹

= = ⋯ =

= 0.

c

c

c

t

c

c

c

n

n

1 + t + ⋯ +

c

c

c

t

1, t, , …,

t

_t

W(1, t, … ) =

t

= 1!2!3! …n!

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

1

0

0

0

⋮

0

t

1!

0

0

⋮

0

t

2t

2!

0

⋮

0

t

3t

3!t

3!

⋮

0

…

…

…

…

⋱

…

t

nt

n(n − 1)t

n(n − 1)(n − 2)t

⋮

n!

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

, t ,

, …,

e

_e

_t

_e

_t

_e

(45)

PRZYKŁAD

Przykład 15:

Przykład 15:

Jeżeli weźmiemy liniową kombinację tych funkcji i przyrównamy ją do zera

a w miejsce podstawimy wówczas i Zatem

równość ta zachodzi, gdy ponieważ niezerowy wielomian może mieć

co najwyżej różnych pierwiatków rzeczywistych.

Analogicznie, jeżeli w tożsamości Liniowa zależnośc i niezależność funkcji-( 5 ) w miejsce podstawimy

dla których i to otrzymujemy równość

a ta zachodzi, gdy i to kończy dowód liniowej niezależności danego zbioru funkcji.

WNIOSEK

Wniosek 3:

Wniosek 3:

Z przykładu Liniowa zależnośc i niezależność funkcji-6 wynika, że funkcje

są liniowo niezależne.

PRZYKŁAD

Przykład 16:

Przykład 16:

Funkcje są liniowo niezależne, jeżeli gdy

W celu pokazania liniowej niezależności powyższych funkcji, liczymy ich wrońskian

sin(αt), tsin(αt), …, sin(αt), cos(αt), tcos(αt), …, cos(αt)

t

_t

( sin(αt) + cos(αt)) = 0, t ∈ R

∑

t

_c

d

t

t

=

, (k ∈ Z)

sin(α ) = 1

t

cos(α ) = 0.

t

1 +

+ ⋯ +

= 0, k ∈ Z

c

c

t

c

t

= = ⋯ =

= 0,

c

c

c

c

1 + t + ⋯ +

c

c

t

n

t

=

, (k ∈ Z),

t~

sin(α ) = 0

t~

cos(α ) = 1,

t~

1 +

+ ⋯ +

= 0, k ∈ Z,

d

d

t~

d

t~

=

= ⋯ =

= 0

d

d

d

sin(αt),

t sin(αt), …,

sin(αt), cos(αt), tcos(αt), …,

cos(αt)

e

_e

_e

_t

_e

_e

_e

_t

,

, …,

e

_e

_e

_λ

_{≠ ,}

λ

i ≠ j.

=

=

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣

∣