Asymptota ukośna wykresu funkcji

(1)

Granica funkcji jednej

zmiennej rzeczywistej

Autorzy:

Katarzyna Czyżewska

(2)

Spis treści

Definicja granicy funkcji w punkcie i w nieskończoności Granice jednostronne i WKW istnienia granicy funkcji Symbole oznaczone i nieoznaczone w granicy funkcji Własności granic funkcji

Granice pewnych funkcji specjalnych Metody obliczania granic funkcji Asymptota pionowa wykresu funkcji Asymptota ukośna wykresu funkcji

(3)

Definicja granicy funkcji w punkcie i w

nieskończoności

DEFINICJA

Definicja 1: Otoczenie i sąsiedztwo punktu

Otoczeniem punktu nazywamy dowolny przedział otwarty zawierający ten punkt, tzn. , a sąsiedztwem punktu nazywamy otoczenie z wyłączeniem punktu .

Oznaczenia Oznaczenia

Otoczenie punktu oznaczamy symbolicznie , a sąsiedztwo punktu oznaczamy przez .

Komentarz Komentarz

W wielu sytuacjach, przy badaniu własności funkcji , gdzie interesuje nas tylko jej zachowanie w bliskim sąsiedztwie punktu w którym funkcja nie musi być określona. Zawężamy wtedy funkcję do otoczenia lub sąsiedztwa punktu , zamiast zajmować się całą dziedziną funkcji. Jeżeli funkcja posiada pewną własność w otoczeniu lub sąsiedztwie, które może być nawet bardzo małe, punktu , to mówimy o lokalnym zachowaniu się funkcji. Pojęcie granicy funkcji w punkcie należy właśnie do takiej kategorii własności.

DEFINICJA

Definicja 2: Definicja Cauchy'ego granicy właściwej funkcji w punkcie

Mówimy, że funkcja ma granicę w punkcie , gdzie pewne sąsiedztwo jest zawarte w dziedzinie funkcji, jeżeli dla dowolnego otoczenia punktu da się dobrać sąsiedztwo punktu tak, aby dla wszystkich argumentów z tego sąsiedztwa, wartości funkcji dla tych argumentów wpadały do otoczenia punktu .

Oznaczenia Oznaczenia

Granicę funkcji w punkcie oznaczamy przez

UWAGA

Uwaga 1:

Definicję Cauchy’ego granicy właściwej funkcji w punkcie można zapisać symbolicznie: funkcja ma w punkcie granicę równą wtedy i tylko wtedy, gdy

.

∈ R

x

0

(a, b)

x

0

∈ (a, b)

∈ R

x

0

x

0

∈ R

x

0

R

(4)

ε f(x) x g +

}

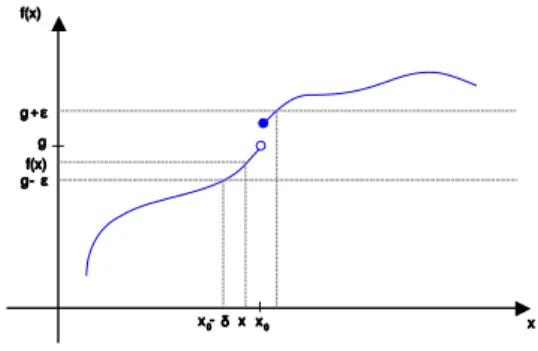
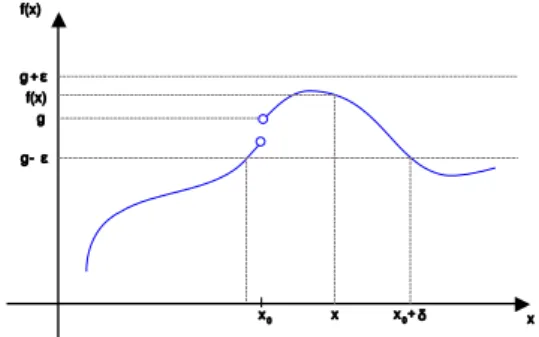
x0 x f(x) δ x0+ δ x0 -δ ε g-g

Rysunek 1: Interpretacja geometryczna definicji Cauchy'ego granicy funkcji w punkcie

Na Rys. 1 widzimy wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest granicą funkcji w punkcie . W tym celu bierzemy dowolne i wyznaczamy przedział , który przedłużamy do pasa wzdłuż osi odciętych. Wyznaczamy punkty przecięcia prostych i z wykresem funkcji , które rzutujemy prostopadle na oś odciętych. Przez oznaczymy najmniejszą z odległości zrzutowanych punktów od punktu . Pokazujemy, że dla dowolnego argumentu należącego do przedziału wartość funkcji dla tego argumentu wpada do przedziału

, co spełnia warunki definicji Cauchy’ego granicy funkcji w punkcie.

DEFINICJA

Definicja 3: Definicja Heinego granicy właściwej funkcji w punkcie

Mówimy, że funkcja ma granicę w punkcie , gdzie pewne sąsiedztwo jest zawarte w dziedzinie funkcji, jeżeli dla każdego nie stałego ciągu argumentów funkcji różnych od zbieżnego do granicy , ciąg wartości funkcji odpowiadających argumentom jest zbieżny do granicy .

UWAGA

Uwaga 2:

Definicję Heinego granicy właściwej funkcji w punkcie można zapisać symbolicznie symbolicznie: funkcja ma w punkcie granicę równą wtedy i tylko wtedy, gdy

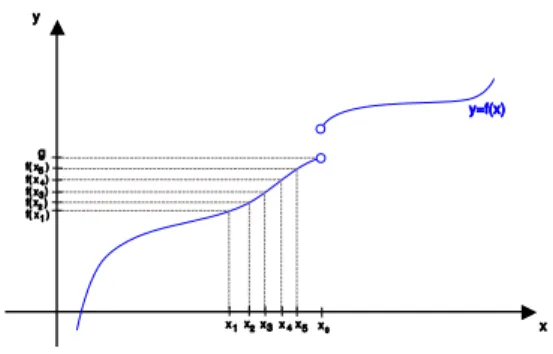
. x0 x f(x) x x x3 x42 1 x x x x 1 2 3 4 f( ) f( ) f( ) f( ) g

Rysunek 2: Interpretacja geometryczna definicji Heinego granicy funkcji w punkcie

(5)

Rys. 2 przedstawia wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest granicą funkcji w punkcie . W tym celu wybieramy kolejne wyrazy ciągu argumentów funkcji różne od , który ma granicę i zaznaczamy na osi rzędnych wartości funkcji dla tych argumentów. Sprawdzamy, czy ciąg wartości funkcji lokalizuje się wokół liczby . Jeżeli tak jest, to spełniony jest warunek definicji Heinego.

UWAGA

Uwaga 3:

Zauważamy, ze definicja Cauchy’ego sformułowana jest w języku otoczeń i jest niewygodna jako narzędzie do wyliczania granicy. Definicja Heinego używa w swojej wypowiedzi pojęcia ciągu, dlatego też okazuje się, że znajomość metod liczenia granic ciągów można wykorzystać przy liczeniu granic funkcji właśnie poprzez bezpośrednie zastosowanie definicji Heinego.

TWIERDZENIE

Twierdzenie 1: o równoważności definicji Cauchy’ego i Heinego

Definicja Heinego granicy funkcji w punkcie jest równoważna odpowiedniej definicji Cauchy'ego

(6)

PRZYKŁAD

Przykład 1:

Pokaż z definicji, że Rozwiązanie: Sposób I:

Skorzystajmy z definicji Cauchy'ego.

Bierzemy zatem dowolne . Mamy pokazać, że znajdziemy takie , że dla wszystkich argumentów i funkcji spełniających zależność zachodzi nierówność

Rozwiązujemy powyższą nierówność wyliczając zależność dla

, dla z drugiej strony dla mamy

co jest równoważne nierówności , czyli możemy przyjąć .

Stąd , dla oraz , dla , czyli dla każdej liczby da się dobrać liczbę taką, że spełniona jest nierówność dla wszystkich takich, że .

Sposób II:

Skorzystajmy z definicji Heinego.

Bierzemy zatem dowolny ciąg taki, że . Mamy pokazać, że Obliczamy granicę To dowodzi, że .

PRZYKŁAD

Przykład 2:

Oblicz z definicji . Rozwiązanie:

Do obliczenia granicy skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg zmierzający do i obliczamy .

Wyliczamy granicę .

Zatem .

(7)

DEFINICJA

Definicja 4: Granica właściwa funkcji w nieskończoności

Mówimy, że funkcja ma granicę w , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest zbieżny do granicy . Mówimy, że funkcja ma granicę w , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest zbieżny do granicy .

UWAGA

Uwaga 4:

Powyższe definicje możemy zapisać symbolicznie wtedy i tylko wtedy, gdy

6

4

2

20 40 60 80

0

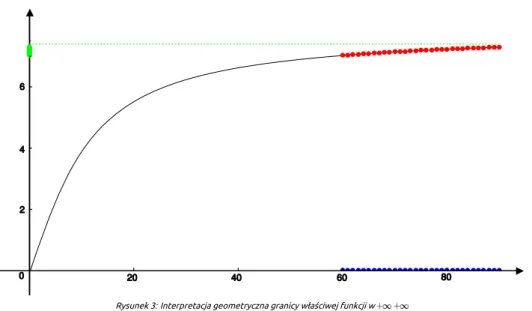
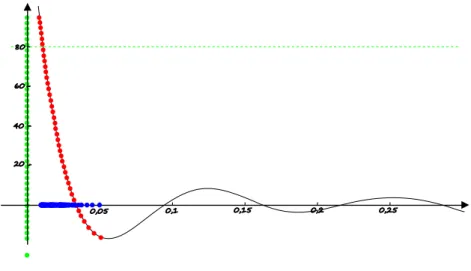
Rysunek 3: Interpretacja geometryczna granicy właściwej funkcji w

Rys. 3 przedstawia wykres funkcji określonej w przedziale oraz metodę wyznaczania granicy funkcji w nieskończoności korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg rozbieżny do (niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg zbieżny, to funkcja ma granicę w nieskończoności, co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy znajdziemy prostą o równaniu , do której wykres funkcji zbliża się nieograniczenie wraz ze wzrostem wartości argumentów.

R

(8)

PRZYKŁAD

Przykład 3:

Oblicz z definicji . Rozwiązanie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów rozbieżny do . Obliczamy granicę ciagu wartości funkcji dla tych argumentów

. Czyli .

PRZYKŁAD

Przykład 4:

Oblicz . Rozwiązanie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg rozbieżny do . Obliczamy granicę wartości funkcji dla tych argumentów

Czyli .

UWAGA

Uwaga 5:

Granica funkcji w nieskończoności jest uogólnieniem pojęcia granicy ciągu, dlatego też wiele własności wyprowadzonych dla granic ciągów stosuje się do granicy funkcji w nieskończoności.

(9)

WNIOSEK

Wniosek 1:

, dla

DEFINICJA

Definicja 5: Granica niewłaściwa funkcji w punkcie

Mówimy, że funkcja ma granicę niewłaściwą w punkcie , jeżeli dla każdego nie stałego ciągu argumentów funkcji różnych od zbieżnego do granicy , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest rozbieżny do .

UWAGA

Uwaga 6:

Powyższe definicje możemy zapisać symbolicznie wtedy i tylko wtedy, gdy

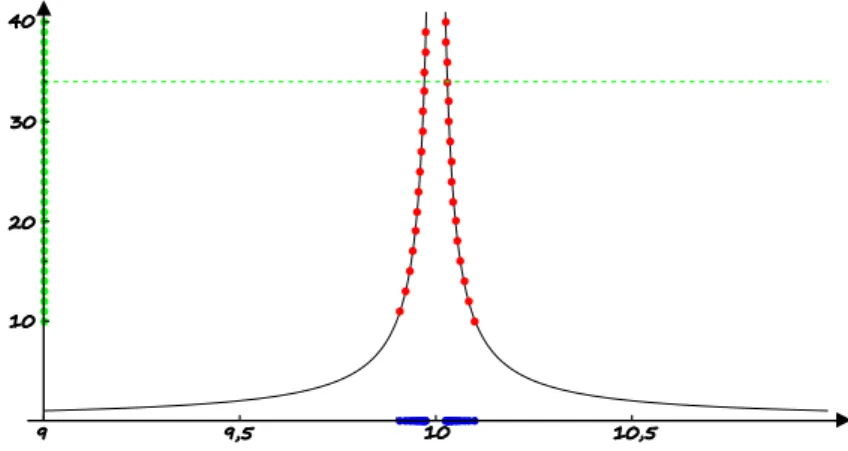
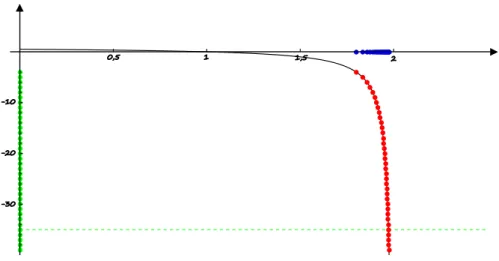
Rysunek 4: Interpretacja geometryczna granicy niewłaściwej funkcji w punkcie

R

(10)

Rys. 4 przedstawia wykres funkcji określonej w sąsiedztwie liczby oraz metodę wyznaczania granicy niewłaściwej funkcji w punkcie korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg zbieżny do (niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg rozbieżny do , to funkcja ma granicę niewłaściwą w punkcie , co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy dla dowolnej prostej o równaniu znajdziemy sąsiedztwo punktu takie, że dla argumentów z tego sąsiedztwa wykres funkcji leży powyżej prostej.

PRZYKŁAD

Przykład 5:

Oblicz granicę . Rozwiązanie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów różnych od i zbieżny do . Obliczamy granicę ciagu wartości funkcji dla tych argumentów

.

Czyli .

DEFINICJA

Definicja 6: Granica niewłaściwa funkcji w nieskończoności

Mówimy, że funkcja ma granicę w , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest rozbieżny do .

UWAGA

Uwaga 7:

Powyższe definicje możemy zapisać symbolicznie

wtedy i tylko wtedy, gdy .

(11)

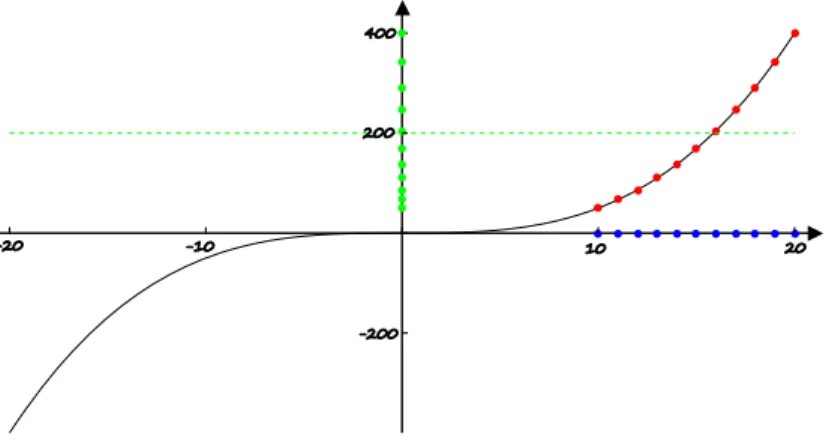
Rysunek 5: Interpretacja geometryczna granicy niewłaściwej funkcji w

Rys. 5 przedstawia wykres funkcji określonej w całym zbiorze liczb rzeczywistych oraz metodę wyznaczania granicy niewłaściwej funkcji w nieskończoności, korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg rozbieżny do (niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg rozbieżny do , to funkcja ma granicę niewłaściwą w nieskończoności , co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy dla dowolnej prostej o równaniu znajdziemy na osi odciętych przedział taki, że dla argumentów z tego przedziału wykres funkcji leży powyżej prostej.

PRZYKŁAD

Przykład 6:

Oblicz granicę . Rozwiąznie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów rozbieżny do . Obliczamy granicę ciągu wartości funkcji dla tych argumentów

.

Czyli .

Granice jednostronne i WKW istnienia granicy funkcji

DEFINICJA

Definicja 7: Lewostronne sąsiedztwo punktu

(12)

DEFINICJA

Definicja 8: Prawostronne sąsiedztwo punktu

Prawostronnym sąsiedztwem punktu nazywamy dowolny przedział otwarty, którego lewym końcem jest punkt .

UWAGA

Uwaga 8: Oznaczenie sąsiedztwa

Lewostronne sąsiedztwo punktu oznaczamy przez , dla pewnego a prawostronne sąsiedztwo punktu przez dla pewnego .

DEFINICJA

Definicja 9: Definicja Cauchy'ego właściwej granicy lewostronnej funkcji w

punkcie

Mówimy, że funkcja ma granicę lewostronną w punkcie równą , jeżeli dla dowolnego otoczenia punktu da się dobrać lewostronne sąsiedztwo punktu zawarte w dziedzinie funkcji tak, aby dla wszystkich argumentów z tego sąsiedztwa, wartości funkcji dla tych argumentów wpadały do otoczenia punktu .

ε f(x) x g + x0 x f(x) δ x0 -ε g-g

Rysunek 6: Interpretacja geometryczna definicji Cauchy'ego granicy lewostronnej funkcji w punkcie

Rys. 6 przedstawia wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w lewostronnym sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest granicą lewostronną funkcji w punkcie . W tym celu bierzemy dowolne i wyznaczamy przedział , który

przedłużamy do pasa wzdłuż osi odciętych. Wyznaczamy punkty przecięcia prostych i z wykresem funkcji , które rzutujemy prostopadle na oś odciętych. Przez oznaczymy odległość punktu od tego ze zrzutowanych punktów, który leży na lewo od punktu . Pokazujemy, że dla dowolnego argumentu należącego do przedziału wartość funkcji dla tego argumentu wpada do przedziału , co spełnia warunki definicji Cauchy’ego granicy lewostronnej funkcji w punkcie.

R

(13)

DEFINICJA

Definicja 10: Definicja Cauchy'ego właściwej granicy prawostronnej funkcji w

punkcie

Mówimy, że funkcja ma granicę prawostronną w punkcie równą , jeżeli dla dowolnego otoczenia punktu da się dobrać prawostronne sąsiedztwo punktu zawarte w dziedzinie funkcji tak, aby dla wszystkich argumentów z tego sąsiedztwa, wartości funkcji dla tych argumentów wpadały do otoczenia punktu .

ε f(x) x g + x0 x f(x) δ x0+ ε g-g

Rysunek 7: Interpretacja geometryczna definicji Cauchy'ego granicy prawostronnej w punkcie

Rys. 7 przedstawia wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w prawostronnym sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest granicą prawostronną funkcji w punkcie . W tym celu bierzemy dowolne i wyznaczamy przedział , który przedłużamy do pasa wzdłuż osi odciętych. Wyznaczamy punkty przecięcia prostych i z wykresem funkcji , które rzutujemy prostopadle na oś odciętych. Przez oznaczymy odległość punktu od tego ze zrzutowanych punktów, który leży na prawo od punktu . Pokazujemy, że dla dowolnego argumentu należącego do przedziału wartość funkcji

dla tego argumentu wpada do przedziału , co spełnia warunki definicji Cauchy’ego granicy prawostronnej funkcji w punkcie.

UWAGA

Uwaga 9: Oznaczenie granicy lewostroonej w punkcie

Granicę lewostronną funkcji w punkcie oznaczamy przez , a granicę prawostronną przez . Powyższe definicje możemy zapisać symbolicznie

wtedy i tylko wtedy, gdy wtedy i tylko wtedy, gdy

DEFINICJA

Definicja 11: Defincija Heinego właściwej granicy lewostronnej funkcji w punkcie

Mówimy, że funkcja ma granicę lewostronną w punkcie równą , jeżeli dla dowolnego ciągu

argumentów funkcji o wyrazach mniejszych od zbieżnego do granicy , ciąg wartości funkcji dla wyrazów ciągu ma granicę równą .

R

(14)

x0 x x x x x1 2 3 4 x x x x 1 2 34 f( ) f( ) f( ) f( ) g y y=f(x) x5 x f(5)

Rysunek 8: Interpretacja geometryczna definicji Heinego granicy lewostronnej funkcji w punkcie

Rys. 8 przedstawia wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w lewostronnym sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest lewostronną granicą funkcji w punkcie . W tym celu wybieramy kolejne wyrazy ciągu argumentów funkcji

mniejsze od który ma granicę i zaznaczamy na osi rzędnych wartości funkcji dla tych argumentów. Sprawdzamy, czy ciąg wartości funkcji lokalizuje się wokół liczby . Jeżeli tak jest, to spełniony jest warunek definicji Heinego.

DEFINICJA

Definicja 12: Definicja Heinego właściwej granicy prawostronnej funkcji w

punkcie

Mówimy, że funkcja ma granicę prawostronną w punkcie równą , jeżeli dla dowolnego ciągu

argumentów funkcji o wyrazach większych od zbieżnego do granicy , ciąg wartości funkcji dla wyrazów ciągu ma granicę równą . x0 x4x3x2x1 x x x x x 1 2 3 4 f( ) f( ) f( ) f( ) g y y=f(x) x5 x f(5)

Rysunek 9: Interpretacja geometryczna definicji Heinego granicy prawostronnej funkcji w punkcie

Rys. 9 przedstawia wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w prawostronnym sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest prawostronną granicą funkcji w punkcie . W tym celu wybieramy kolejne wyrazy ciągu argumentów funkcji

większe od który ma granicę i zaznaczamy na osi rzędnych wartości funkcji dla tych argumentów. Sprawdzamy, czy ciąg wartości funkcji lokalizuje się wokół liczby . Jeżeli tak jest, to spełniony jest warunek definicji Heinego.

(15)

UWAGA

Uwaga 10:

Powyzsze definicje możemy zapisać symbolicznie wtedy i tylko wtedy, gdy wtedy i tylko wtedy, gdy

DEFINICJA

Definicja 13: Heinego niewłaściwej granicy lewostronnej funkcji w punkcie

Mówimy, że funkcja ma granicę lewostronną w punkcie równą , jeżeli dla dowolnego ciągu argumentów funkcji o wyrazach mniejszych od zbieżnego do granicy , ciąg wartości funkcji dla wyrazów ciągu

jest rozbieżny do albo do .

Rysunek 10: Interpretacja geometryczna definicji Heinego niewłaściwej granicy lewostronnej

Rys. 10 przedstawia wykres funkcji określonej w lewostronnym sąsiedztwie liczby oraz metodę wyznaczania granicy niewłaściwej funkcji w punkcie korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg zbieżny do

(niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg rozbieżny do , to funkcja ma granicę niewłaściwą w punkcie , co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy dla dowolnej prostej o równaniu znajdziemy lewostronne sąsiedztwo punktu takie, że dla argumentów z tego sąsiedztwa wykres funkcji leży poniżej prostej.

(16)

DEFINICJA

Definicja 14: Heinego niewłaściwej granicy prawostronnej funkcji w punkcie

Mówimy, że funkcja ma granicę prawostronną w punkcie równą , jeżeli dla dowolnego ciągu argumentów funkcji o wyrazach większych od zbieżnego do granicy , ciąg wartości funkcji dla wyrazów ciągu jest rozbieżny do albo do .

Rysunek 11: Interpretacja geometryczna definicji Heinego niewłaściwej granicy prawostronnej

Rys. 11 przedstawia wykres funkcji określonej w prawostronnym sąsiedztwie liczby oraz metodę wyznaczania granicy niewłaściwej funkcji w punkcie korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg zbieżny do

(niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg rozbieżny do , to funkcja ma granicę niewłaściwą w punkcie , co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy dla dowolnej prostej o równaniu znajdziemy prawostronne sąsiedztwo punktu takie, że dla argumentów z tego sąsiedztwa wykres funkcji leży powyżej prostej.

UWAGA

Uwaga 11:

Powyzsze definicje możemy zapisać symbolicznie wtedy i tylko wtedy, gdy wtedy i tylko wtedy, gdy

UWAGA

Uwaga 12:

Zauważmy, że nie da się zdefiniować jednostronnych granic funkcji w nieskończoności, ponieważ nie ma prawostronnego sąsiedztwa, a nie ma sąsiedztwa lewostronnego.

(17)

TWIERDZENIE

Twierdzenie 2: WKW istnienia granicy funkcji

Funkcja ma w punkcie granicę właściwą równą wtedy i tylko wtedy, gdy obydwie granice jednostronne w punkcie równe są .

UWAGA

Uwaga 13:

Warunek konieczny i wystarczający istnienia granicy funkcji prawdziwy jest również dla granic niewłaściwych funkcji w punkcie.

PRZYKŁAD

Przykład 7:

Zbadaj istnienie granicy . Rozwiązanie:

Badamy granice jednostronne funkcji w punkcie uwzględniając znak wyrażenia pod wartością bezwzględną

Obydwie granice jdnostronne są równe, czyli .

PRZYKŁAD

Przykład 8:

Zbadaj istnienie granicy . Badamy granice jednostronne w punkcie

(18)

PRZYKŁAD

Przykład 9:

Oblicz granice jednostronne w punkcie funkcji Rozwiązanie:

Korzystamy z faktu, że oraz .

z wykresu funkcji wykładniczej odczyujemy, że i . Obliczamy granice jednostronne

. Ponieważ granice jednostronne są takie same, to .

PRZYKŁAD

Przykład 10:

Oblicz granice jednostronne w punkcie funkcji . Rozwiazanie:

Korzystamy z faktu, że oraz .

Z wykresu funkcji cyklometrycznej odczytujemy i . Obliczamy granice jednostronne

Ponieważ granice jednostronne sa różne, to funkcja nie ma granicy w punkcie .

Symbole oznaczone i nieoznaczone w granicy funkcji

Obliczając granice funkcji poprzez zastąpienie jej argumentu wartością graniczną, do której zmierza argument, otrzymujemy symbole graniczne ujmowane w nawiasy kwadratowe, w celu zaznaczenia, że są to wyrażenia otrzymywane przy obliczaniu granic, a nie działania arytmetyczne na liczbach. Należy na tę symbolikę zwracać szczególną uwagę zwłaszcza w sytuacji, gdy

otrzymujemy zero w mianowniku, albo wyrażenia zmierzające do nieskończoności. Niektóre z symboli granicznych dają zawsze ten sam wynik, bez względu na to w granicach jakich funkcji otrzymujemy określony symbol i nazywamy je symbolami oznaczonymi. Inne znów dają różne wyniki w zależności od funkcji, której granicę liczymy i takie symbole nazywamy nieoznaczonymi.

(19)

DEFINICJA

Definicja 15: Symbol oznaczony i nieoznaczony

Symbolem oznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i które daje zawsze taki sam wynik niezależny od typu funkcji, w granicy której otrzymuje się dany symbol graniczny.

Symbolem nieoznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i którego wartości nie da się jednoznacznie obliczyć na podstawie jedynie granic funkcji składowych, z których powstaje symbol graniczny i wynik zależy od typu funkcji, w granicy której otrzymuje się dany symbol graniczny.

UWAGA

Uwaga 14:

Do obliczania symboli oznaczonych służą odpowiednie twierdzenia podające wartości konkretnych symboli granicznych. Nie istnieją natomiast ogólne twierdzenia pozwalające obliczyć wartość symbolu nieoznaczonego i w każdym przypadku indywidualnie należy, stosując odpowiednie przekształcenie algebraiczne, zamienić symbol nieoznaczony na oznaczony. Jedną z metod stosowanych do obliczania granic funkcji, które prowadzą do symbolu nieoznaczonego, jest odpowiednie zastosowanie reguły de l’Hospitala.

TWIERDZENIE

Twierdzenie 3: o symbolach oznaczonych

Niech będzie dowolną liczbą rzeczywistą. Symbolami oznaczonymi są

gdzie symbol oznacza granicę funkcji o wartościach dodatnich, która wynosi zero, a symbol granicę funkcji o wartościach ujemnych, która wynosi zero.

(20)

PRZYKŁAD

Przykład 11:

PRZYKŁAD

Przykład 12:

PRZYKŁAD

Przykład 13:

Zauważmy, że , czyli dla zmierzających do funkcja zmierza do granicy po wartościach dodatnich, co zapisujemy . Obliczamy granicę

.

TWIERDZENIE

Twierdzenie 4: o symbolach nieoznaczonych

Symbolami nieoznaczonymi są

(21)

PRZYKŁAD

Przykład 14:

Wykaż, że symbol jest nieoznaczony. Rozwiązanie:

Wiemy, że .

Obliczamy dwie różne granice, które dają ten sam symbol nieoznaczony , ale różne wyniki końcowe .

Świadczy to o tym, że nie da się w sposób jednoznaczny okreslić wartości symbolu .

PRZYKŁAD

Przykład 15:

Wykaż, że symbol jest nieoznaczony. Rozwiąznie:

Znajdziemy dwie funkcje, które w granicach dają ten sam symbol graniczny , ale różne wyniki końcowe

Różne wyniki dowodzą, że nie da się w sposób jednoznaczny okreslić wartości symbolu .

PRZYKŁAD

Przykład 16:

Wykaż, że symbol jest nieoznaczony. Rozwiąznie:

Znajdziemy dwie funkcje, które daja ten sam symbol graniczny , ale różne wyniki końcowe uzyskane za pomocą znanej granicy funkcji .

(22)

UWAGA

Uwaga 15:

Twierdzenia o symbolach oznaczonych i nieoznaczonych stosują się też do granic jednostronnych.

PRZYKŁAD

Przykład 17:

Zbadaj istnienie granicy . Rozwiazanie:

Zauważmy, że wyrażenie jest dodatnie dla i ujemne dla , zatem oraz . Obliczamy teraz granice jednostronne i sprawdzimy, czy są równe.

Ponieważ granice jednostronne są różne, to badana funkcja nie ma granicy w punkcie .

PRZYKŁAD

Przykład 18:

Oblicz granice jednostronne funkcji w punkcie . Rozwiązanie:

Pomocniczo obliczymy granice jednostronne wykładnika oraz

Skorzystamy z wykresu funkcji wykładniczej , z którego odczytujemy i . Zatem

Własności granic funkcji

(23)

TWIERDZENIE

Twierdzenie 5:

Twierdzenie 5: o działaniach

o działaniach arytmetycznych na granicach funkcji

arytmetycznych na granicach funkcji

Niech funkcje i będą określone w pewnym sąsiedztwie punktu . Jeżeli oraz , to

UWAGA

Uwaga 16:

Twierdzenie o działaniach arytmetycznych na granicach funkcji stosuje się również do granic jednostronnych w punkcie oraz granic w nieskończoności. W przypadku, gdy jedna lub obydwie funkcje mają granice niewłaściwe działania arytmetyczne na granicach tych funkcji prowadzą do symboli oznaczonych lub nieoznaczonych.

PRZYKŁAD

Przykład 19:

Oblicz granicę . Rozwiązanie: Rozwiązanie:

Z twierdzenia o działaniach arytmetycznych na granicach funkcji obliczamy granice

oraz Funkcja jest określona w otoczeniu punktu i , a funkcja jest określona w otoczeniu punktu i . Z twierdzenia o działaniach arytmetycznych na granicach funkcji obliczamy granicę

(24)

PRZYKŁAD

Przykład 20:

Oblicz granicę Rozwiązanie: Rozwiązanie:

Obliczamy oraz . Funkcja jest określona w otoczeniu punktu , czyli i funkcja jest określona w otoczeniu punktu , a zatem . Korzystając z twierdzenia o działaniach arytmetycznych na granicach funkcji obliczamy granicę

TWIERDZENIE

Twierdzenie 6:

Twierdzenie 6: o dwóch funkcjach

o dwóch funkcjach

Jeżeli dla wszystkich z pewnego sąsiedztwa punktu zachodzi nierówność oraz istnieją granice i , to

UWAGA

Uwaga 17:

Twierdzenie o dwóch funkcjach zachodzi również dla granic jednostronnych i wtedy w założeniach odpowiednią nierówność badamy w sąsiedztwie jednostronnym punktu , a także dla granic w nieskończonościach i wtedy nierówność badamy dla argumentów większych od pewnej liczby , w przypadku , albo dla argumentów mniejszych od pewnej liczby , w przypadku .

(25)

PRZYKŁAD

Przykład 21:

Ponieważ , a funkcja nie ma granicy w , nie możemy skorzystać z twierdzenia o działaniach arytmetycznych na granicach funkcji. Skorzystamy z twierdzenia o dwóch funkcjach i nierówności dla funkcji cosinus .

Granica , czyli , a zatem granica funkcji o wartościach większych lub równych wartościom funkcji w lewostronnym sąsiedztwie punktu nie może być mniejsza, a zatem

PRZYKŁAD

Przykład 22:

Obliczamy granice pomocnicze , czyli oraz

, czyli .

Otrzymujemy symbol nieoznaczony . Skorzystamy z twierdzenia o dwóch

funkcjach wiedząc, że dla zachodzi nierówność .

Ponieważ , to funkcja o wartościach mniejszych od w prawostronnym sąsiedztwie punktu nie może mieć granicy od niej większej, a zatem

TWIERDZENIE

Twierdzenie 7:

Twierdzenie 7: o trzech funkcjach

o trzech funkcjach

Jeżeli dla wszystkich z pewnego sąsiedztwa punktu zachodzą nierówności oraz , to wówczas istnieje granica .

(26)

UWAGA

Uwaga 18:

Twierdzenie o trzech funkcjach zachodzi również dla granic jednostronnych i wtedy w założeniach odpowiednie nierówności badamy w sąsiedztwie jednostronnym punktu , a także dla granic w nieskończonościach i wtedy nierówności badamy dla argumentów większych od pewnej liczby , w przypadku , albo dla argumentów mniejszych od pewnej liczby , w przypadku .

PRZYKŁAD

Przykład 23:

Ponieważ dla funkcje oraz nie mają granic, zastosujemy twierdzenie o trzech funkcjach pamiętając, że zbiorem wartości funkcji sinus i cosinus jest przedział .

Zauważamy, że funkcja wykładnicza ma w granicę równą . Obliczamy granice funkcji skrajnych oraz

.

Ponieważ w dowolnym przedziale zachodzą nierówności pomiędzy wartościami trzech funkcji i granice funkcji skrajnych w są takie same, to

(27)

PRZYKŁAD

Przykład 24:

Obliczamy granice pomocnicze , a funkcja ma w granicę niewłaściwą , to otrzymujemy symbol nieoznaczony . Skorzystamy z twierdzenia o trzech funkcjach i faktu, że funkcja

jest rosnąca, a zatem dla mamy

oraz . Czyli

Korzystając z twierdzeń o logarytmach obliczamy granice

oraz . Ponieważ w dowolnym przedziale dla

zachodzą nierówności pomiędzy wartościami trzech funkcji i granice w funkcji skrajnych są równe, to

TWIERDZENIE

Twierdzenie 8:

Twierdzenie 8: o granicy iloczynu funkcji ograniczonej i mającej granicę zero

o granicy iloczynu funkcji ograniczonej i mającej granicę zero

Jeżeli funkcje i są określone w pewnym sąsiedztwie punktu i w tym sąsiedztwie funkcja jest

ograniczona, a funkcja ma granicę równą zero w punkcie , to granica iloczynu funkcji i w punkcie jest równa zero.

UWAGA

Uwaga 19:

(28)

PRZYKŁAD

Przykład 25:

Zauważamy, że , a funkcja nie ma granicy w nieskończoności. Zbiorem wartości funkcji jest przedział , a zatem jest to funkcja ograniczona w całym zbiorze liczb rzeczywistych. Liczymy granicę drugiego czynnika . Z twierdzenia o granicy iloczynu funkcji ograniczonej i mającej granicę zero otrzymujemy

PRZYKŁAD

Przykład 26:

Ponieważ , a funkcja nie ma granicy w nieskończoności, dlatego nie możemy zastosować twierdzenia o działaniach arytmetycznych na granicach funkcji, zauważmy jednak, że funkcja jest ograniczona w całym zbiorze liczb rzeczywistych. Obliczmy więc granicę pozostałego czynnika

Z twierdzenia o granicy iloczynu funkcji ograniczonej i mającej granicę zero otrzymujemy

TWIERDZENIE

Twierdzenie 9:

Twierdzenie 9: o zamianie zmiennej w granicy

o zamianie zmiennej w granicy

Jeżeli funkcja jest określona w sąsiedztwie punktu , i w pewnym sąsiedztwie punktu wartości funkcji są różne od oraz funkcja jest określona w pewnym sąsiedztwie punktu i ma granicę w tym punkcie, to

(29)

UWAGA

Uwaga 20:

Twierdzenie o zamianie zmiennej w granicy prawdziwe jest również dla granic jednostronnych i granic w

nieskończonościach. Należy jednak zwracać uwagę na to, gdzie określona jest funkcja dla argumentów należących do jednostronnego sąsiedztwa punktu w przypadku granic jednostronnych, albo do przedziałów jednostronnie

nieograniczonych w przypadku granic w nieskończonościach.

PRZYKŁAD

Przykład 27:

Dokonajmy zamiany zmiennej w badanej funkcji i niech . Obliczamy granicę nowej zmiennej

. Zapisujemy funkcję jako funkcję nowej zmiennej w postaci funkcji . Funkcje i są określone w otoczeniu punktu . Korzystamy z twierdzenia o zamianie zmiennej w granicy pamiętając, że

.

PRZYKŁAD

Przykład 28:

Dokonujemy zamiany zmiennej podstawiając . Obliczamy granicę nowej zmiennej . Badana funkcja zapisuje się jako funkcja nowej zmiennej jako . Korzystamy z twierdzenia o zamianie zmiennej w

granicy pamiętając, że .

Granice pewnych funkcji specjalnych

(30)

TWIERDZENIE

Twierdzenie 10: o granicach pewnych funkcji specjalnych

dla

PRZYKŁAD

Przykład 29:

Oblicz granicę . Rozwiązanie: Rozwiązanie: Zauważamy, że .

Aby obliczyć granicę dokonujemy zamiany zmiennej i obliczamy granicę . Korzystamy z twierdzenia o zamianie zmiennej w granicy otrzymując . Wiemy również, że funkcja ma w punkcie zero granicę równą jeden, a zatem

PRZYKŁAD

Przykład 30:

Zauważmy, że . Dokonujemy zamiany zmiennej podstawiając i obliczamy granicę . Korzystamy z twierdzenia o zamianie zmiennej w granicy otrzymując

(31)

TWIERDZENIE

Twierdzenie 11: o granicach pewnych funkcji, które w zerze mają granicę jeden

II

2 II

II

2 I

y=x

y=sinx

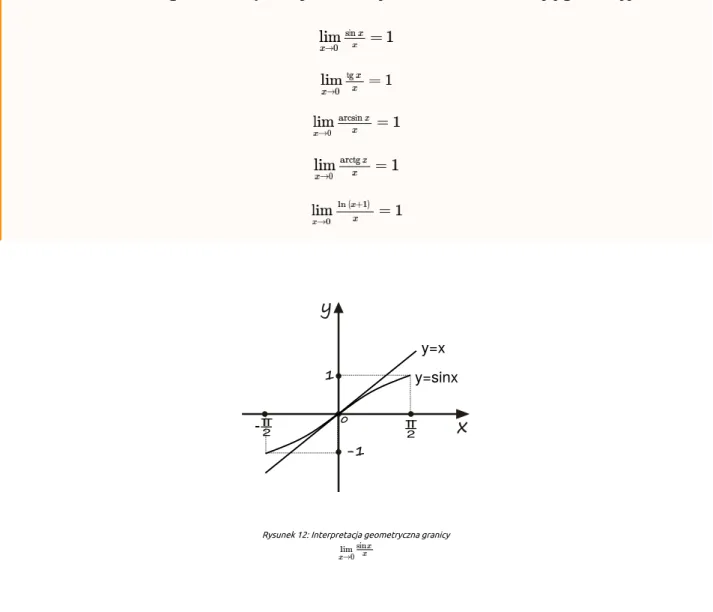
Rysunek 12: Interpretacja geometryczna granicy

Komentarz Komentarz

Rys. 12 przedstawia wykresy funkcji oraz w otoczeniu punktu . Zauważamy, że jeżeli przyjrzymy się bliżej małemu otoczeniu punktu zero, to wykresy obydwu funkcji są prawie nierozróżnialne, dlatego też w granicy, przy argumencie

zmierzającym do zera granica ilorazu tych funkcji wynosi . Czyli symbol nieoznaczony , który otrzymujemy licząc granicę w tym szczególnym przypadku daje wartość . Analogicznie, analizując wykresy pozostałych funkcji występujących w innych podpunktach powyższego twierdzenia, otrzymujemy w granicy taki sam wynik.

(32)

PRZYKŁAD

Przykład 31:

W celu obliczenia granicy dokonujemy zamiany zmiennej podstawiając , przy czym . Mamy zatem

PRZYKŁAD

Przykład 32:

Oblicz granicę Rozwiązanie: Rozwiązanie:

W celu obliczenia granicy dokonujemy zamiany zmiennej podstawiając , przy czym , a w celu obliczenia granicy dokonujemy zamiany zmiennej podstawiając , przy czym . Mamy zatem

(33)

PRZYKŁAD

Przykład 33:

Zauważamy, że . W celu obliczenia granicy dokonujemy zamiany zmiennej podstawiając , wtedy i granica nowej zmiennej . Korzystamy z twierdzenia o zamianie zmiennej w granicy oraz wzoru redukcyjnego otrzymując

Aby obliczyć granicę jeszcze raz dokonujemy zmiany zmiennej podstawiając , przy czym , a zatem

Metody obliczania granic funkcji

Komentarz Komentarz

Do obliczania granic funkcji w przypadku, gdy prowadzą one do symboli nieoznaczonych stosuje się znane metody obliczania granic ciągów, takie jak wyłączanie przed nawias odpowiednich wyrażeń, rozszerzanie o odpowiednio skonstruowaną jedynkę, korzystanie ze wzorów skróconego mnożenia, wzorów trygonometrycznych, własności odpowiednich funkcji. Metody te stosujemy zarówno do granicy funkcji w punkcie, jak i nieskończości oraz do granicy jednostronnej.

PRZYKŁAD

Przykład 34:

Zauważamy, że . W liczniku badanej funkcji wykorzystujemy wzór skróconego mnożenia na różnicę sześcianów otrzymując

(34)

PRZYKŁAD

Przykład 35:

Zauważamy, że . Rozszerzamy wyrażenie mnożąc i dzieląc przez .

PRZYKŁAD

Przykład 36:

Zauważamy, że . Rozszerzamy wyrażenie mnożąc i dzieląc przez .

PRZYKŁAD

Przykład 37:

Zauważamy, że . Rozpisujemy licznik ze wzoru skróconego mnożenia na różnicę sześcianów

Rozszerzamy wyrażenie mnożąc i dzieląc przez , a następnie korzystamy ze wzoru na jedynkę trygonometryczną otrzymując

Komentarz Komentarz

W przypadku symboli nieoznaczonych lub w wielu przypadkach wykorzystujemy granice pewnych funkcji specjalnych, które w granicach dają właśnie takie symbole. Często do obliczenia tych granic stosujemy też twierdzenie o zamianie zmiennej w granicy.

(35)

PRZYKŁAD

Przykład 38:

Pomocniczo obliczamy granicę . Wykorzystamy granice znanych funkcji A zatem

PRZYKŁAD

Przykład 39:

Zauważamy, że . Rozpisując podstawę potęgi otrzymujemy

PRZYKŁAD

Przykład 40:

Zauważamy, że . Przekształcamy wyrażenie, aby można było skorzystać z granic pewnych funkcji specjalnych

(36)

PRZYKŁAD

Przykład 41:

Zauważamy, że . Przekształcamy wyrażenie korzystając z własności logarytmów .

Do obliczenia granicy pomocniczej zamieniamy zmienną podstawiając . Ponieważ , to z twierdzenia o zamianie zmiennej w granicy otrzymujemy

a zatem

Komentarz Komentarz

W przypadku, gdy w granicy funkcji otrzymujemy zero w mianowniku i ma to wpływ na wartość granicy, albo gdy otrzymujemy wartość bezwzględną z wyrażenia, które w granicy przyjmuje zero, albo gdy funkcja, której granicę liczymy jest w punkcie obliczania granicy sklejeniem dwóch funkcji (tzn. jest określona innym wzorem w lewostronnym sąsiedztwie punktu, a innym w prawostronnym sąsiedztwie tego punktu), to do obliczania granicy stosujemy WKW istnienia granicy funkcji, czyli liczymy granic jednostronne.

PRZYKŁAD

Przykład 42:

Zauważamy, że . Ponieważ wartość granicy zależy od znaku mianownika, obliczamy granice jednostronne

(37)

PRZYKŁAD

Przykład 43:

Zauważamy, że . Ponieważ w granicy otrzymujemy wartość bezwzględną z wyrażenia, które ma w granicy wartość zero, liczymy granice jednostronne pamiętając, że

Granice jednostronne są równe, więc funkcja ma w punkcie granicę równą zero.

PRZYKŁAD

Przykład 44:

Oblicz granicę funkcji

w punkcie . Rozwiązanie: Rozwiązanie:

Zauważamy, że w punkcie funkcja jest sklejeniem dwóch różnych funkcji, dlatego obliczamy w tym punkcie granice jednostronne

Granice jednostronne są równe, więc funkcja ma w punkcie granicę równą .

Asymptota pionowa wykresu funkcji

(38)

DEFINICJA

Definicja 16: Asymptota pionowa lewostronna

Niech funkcja będzie określona w lewostronnym sąsiedztwie punktu . Prostą nazywamy asymptotą pionową lewostronną wykresu funkcji , jeżeli granica lewostronna funkcji w punkcie jest niewłaściwa

.

DEFINICJA

Definicja 17: Asymptota pionowa prawostronna

Niech funkcja będzie określona w prawostronnym sąsiedztwie punktu . Prostą nazywamy asymptotą pionową prawostronną wykresu funkcji , jeżeli granica prawostronna funkcji w punkcie jest niewłaściwa

.

UWAGA

Uwaga 21:

Jeżeli prosta jest jednocześnie asymptotą pionową lewo i prawostronną wykresu funkcji , to nazywamy ją asymptotą pionową obustronną.

Komentarz Komentarz

Z definicji Asymptota pionowa lewostronna i Asymptota pionowa prawostronna wynika, że dla argumentów zbliżających się do punktu od strony lewej lub prawej, wykres funkcji nieograniczenie (asymptotycznie) zbliża się do prostej nigdy jej nie dotykając. Poszukiwania prostych które mogą być asymptotami pionowymi wykresu funkcji zaczynamy od wyznaczania punktów, które nie należą do dziedziny funkcji, ale w sąsiedztwie lewo lub prawostronnym których funkcja jest określona, a następnie obliczamy odpowiednie granice jednostronne, aby sprawdzić, czy są to granice niewłaściwe.

Rysunek 13: Asymptota pionowa obustronna

Rys. 13 przedstawia wykres funkcji, dla którego prosta o równaniu x=1 jest asymptotą pionowa obustronną. Rzeczywiście zauważamy, że punkt x=1 nie należy do dziedziny funkcji (funkcja nie posiada wartości dla x=1), a granica lewostronna w punkcie x=1 jest niewłaściwa i wynosi - oraz granica prawostronna w punkcie x=1 jest niewłaściwa i wynosi + .

(39)

PRZYKŁAD

Przykład 45:

Wyznacz asymptoty pionowe wykresu funkcji . Rozwiązanie:

Wyznaczamy dziedzinę funkcji , a następnie badamy, czy prosta jest asymptotą pionową wykresu funkcji. W tym celu wyznaczamy granice jednostronne badanej funkcji w punkcie

Ponieważ obydwie granice jednostronne są niewłaściwe, to prosta jest asymptota pionową obustronną.

PRZYKŁAD

Przykład 46:

Wyznaczamy dziedzinę funkcji . Funkcja jest określona w lewostronnym sąsiedztwie punktu i prawostronnym sąsiedztwie punktu , przy czym obydwa punkty nie należą do dziedziny funkcji. Badamy, czy istnieją asymptoty pionowe: lewostronna o równaniu i prawostronna o równaniu licząc odpowiednie granice jednostronne

oraz

Granica lewostronna w punkcie jest niewłaściwa, czyli prosta jest asymptotą pionową lewostronną, a granica prawostronna w punkcie jest właściwa, czyli prosta nie jest asymptotą pionową.

(40)

PRZYKŁAD

Przykład 47:

Wyznaczamy dziedzinę funkcji . Funkcja jest określona w prawostronnym sąsiedztwie punktu i punkt ten nie należy do dziedziny funkcji. Badamy, czy prosta jest asymptotą pionową prawostronną licząc odpowiednią granicę

Granica prawostronna badanej funkcji w punkcie jest niewłaściwa, a zatem prosta jest asymptotą pionową prawostronną.

Asymptota ukośna wykresu funkcji

DEFINICJA

Definicja 18: Asymptota ukośna lewostronna

Prosta jest asymptotą ukośną lewostronną wykresu funkcji , jeżeli jest zbiorem nieograniczonym od dołu oraz granica różnicy wartości funkcji i funkcji liniowej w jest równa zero

.

DEFINICJA

Definicja 19: Asymptota ukośna prawostronna

Prosta jest asymptotą ukośną prawostronną wykresu funkcji , jeżeli jest zbiorem

nieograniczonym od góry oraz granica różnicy wartości funkcji i funkcji liniowej w jest równa zero .

(41)

UWAGA

Uwaga 22:

Jeżeli prosta jest jednocześnie asymptotą ukośną lewo i prawostronną, to nazywamy ją asymptotą obustronną wykresu funkcji .

Jeżeli współczynnik kierunkowy asymptoty ukośnej jest równy zero , to asymptotę ukośną nazywamy asymptotą poziomą.

Komentarz Komentarz

Z definicji Asymptota ukośna prawostronna wynika, że wykres funkcji wraz ze wzrostem argumentów coraz bardziej zbliża się do asymptoty. Z definicji Asymptota ukośna lewostronna wynika, że wykres funkcji dla argumentów zmierzających do coraz bardziej zbliża się do asymptoty.

Zauważamy również, że asymptota pozioma jest szczególnym przypadkiem asymptoty ukośnej, dlatego też, jeżeli okaże się, że istnieje asymptota pozioma lewo lub prawostronna wykresu funkcji, to nie badamy już istnienia asymptoty ukośnej.

Rysunek 14: Wykres funkcji prostej będącej asymptotą ukośną lewo- i prawostronną.

Rys. 14 przedstawia wykres funkcji, dla którego prosta o równaniu jest asymptotą ukośną lewostronną, a prosta

o równaniu jest asymptotą ukośną prawostronną. Rzeczywiście dla ciągu argumentów zmierzających do różnica pomiędzy wartościami badanej funkcji, a wartościami funkcji liniowej dąży do zera. Analogicznie dla ciągu argumentów zmierzających do + różnica pomiędzy wartościami badanej funkcji, a wartościami funkcji liniowej

dąży do zera.

TWIERDZENIE

Twierdzenie 12:

Twierdzenie 12: o współczynnikach asymptoty ukośnej lewostronnej

o współczynnikach asymptoty ukośnej lewostronnej

Jeżeli jest zbiorem nieograniczonym od dołu, to prosta jest asymptotą ukośną lewostronną wtedy i tylko wtedy, gdy oraz i granice te są właściwe.

TWIERDZENIE

Twierdzenie 13:

Twierdzenie 13: o współczynnikach asymptoty ukośnej prawostronnej

o współczynnikach asymptoty ukośnej prawostronnej

Jeżeli jest zbiorem nieograniczonym od góry, to prosta jest asymptotą ukośną prawostronną wtedy i tylko wtedy, gdy oraz i granice te są właściwe.

(42)

WNIOSEK

Wniosek 2:

Aby zbadać, czy istnieje asymptota pozioma lewo lub prawostronna wykresu funkcji , badamy, czy dziedzina funkcji jest zbiorem nieograniczonym od dołu lub od góry, a następnie, czy granice lub są właściwe. Jeżeli tak jest, to prosta jest asymptotą poziomą lewostronną, a prosta asymptotą poziomą prawostronną wykresu funkcji.

PRZYKŁAD

Przykład 48:

Wyznacz asymptoty ukośne wykresu funkcji . Rozwiązanie:

Wyznaczamy dziedzinę funkcji . Dziedzina funkcji jest zbiorem nieograniczonym od dołu i od góry. Badamy, czy istnieje asymptota pozioma lewo i prawostronna wykresu funkcji

Obydwie granice są właściwe, a zatem prosta jest asymptotą poziomą obustronną. Istnienie asymptoty poziomej obustronnej wyklucza istnienie innej asymptoty ukośnej.

(43)

PRZYKŁAD

Przykład 49:

Wyznacz asymptoty ukośne wykresu funkcji Rozwiązanie:

Wyznaczamy dziedzinę funkcji , która jest zbiorem nieograniczonym od dołu i od góry. Badamy istnienie asymptot poziomych lewo i prawostronnej

i .

Obydwie granice są niewłaściwe, a zatem nie istnieją asymptoty poziome.

Badamy istnienie asymptot ukośnych lewo i prawostronnej licząc odpowiednie granice oraz

Widzimy zatem, że współczynnik kierunkowy a równy jest dla asymptoty prawostronnej i dla asymptoty lewostronnej. Obliczamy wartości współczynników dla obydwu asymptot

oraz

Obydwie granice są właściwe, a zatem prosta jest asymptotą ukośną prawostronną, a prosta jest asymptotą ukośną lewostronną.

PRZYKŁAD

Przykład 50:

Wyznaczamy dziedzinę funkcji , która jest zbiorem nieograniczonym od góry i od dołu. Badamy, czy istnieją asymptoty poziome lewo i prawostronna licząc odpowiednie granice

oraz

Obydwie granice są właściwe, a zatem prosta jest asymptotą poziomą prawostronną, a prosta jest asymptotą poziomą lewostronną. Istnienie asymptot poziomych wyklucza istnienie innych asymptot ukośnych.

(44)

PRZYKŁAD

Przykład 51:

Wyznaczamy dziedzinę funkcji , która jest zbiorem nieograniczonym tylko od góry. Badamy istnienie asymptoty poziomej prawostronnej (ze względu na postać dziedziny)

W celu obliczenia ostatniej granicy dokonujemy podstawienia i wyznaczamy granicę

. A zatem , czyli prosta jest asymptotą poziomą prawostronną. Istnienie asymptoty poziomej prawostronnej wyklucza istnienie innej asymptoty ukośnej.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-09 21:09:10

Oryginalny dokument dostępny pod adresem: http://epodreczniki.open.agh.edu.pl/openagh-podreczniki_view.php? categId=4&handbookId=57