Całki niewłaściwe

(1)

Całki niewłaściwe

Autorzy:

Witold Majdak

(2)

Całki niewłaściwe

Autor: Witold Majdak

Właściwości całki ze względu na przedział całkowania (całka I rodzaju)

Przypomnijmy, że pojęcie całki oznaczonej Riemanna zostało przez nas zdefiniowane dla funkcji ograniczonej, określonej na przedziale domkniętym i ograniczonym. Ze względu na praktyczne zastosowania istnieje potrzeba rozszerzenia tego pojęcia na przypadek funkcji działającej na przedziale nieograniczonym lub funkcji nieograniczonej.

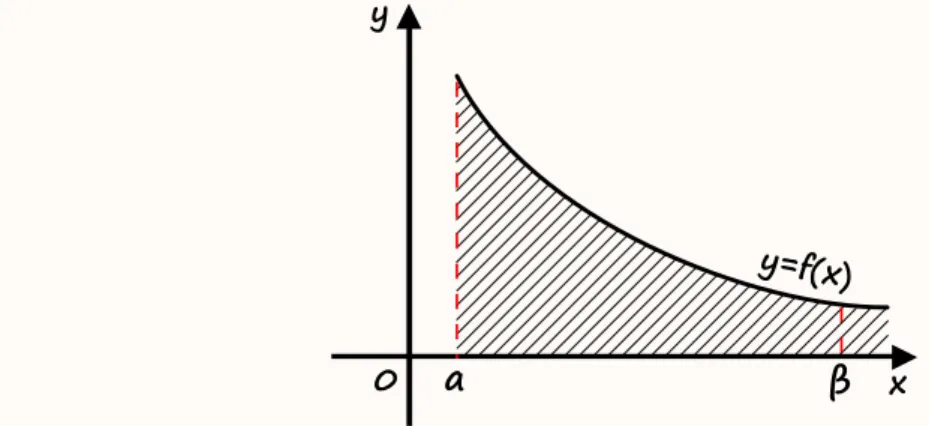
Na początek zdefiniujmy całkę niewłaściwą funkcji określonej na przedziale postaci , następnie , a dalej na

całym zbiorze liczb rzeczywistych.

DEFINICJA

Definicja 1: Całka niewłaściwa Riemanna I rodzaju w przedziale

lub

Niech będzie funkcją całkowalną w sensie Riemmana na każdym z przedziałów domkniętych , gdzie

. Całką niewłaściwą Riemanna I rodzajuCałką niewłaściwą Riemanna I rodzaju funkcji nazywamy granicę

i oznaczamy ją symbolem

.

Jeżeli powyższa granica istnieje i jest skończona, to mówimy, że całka niewłaściwa jest zbieżnazbieżna, natomiast jeżeli granica ta nie istnieje lub jest niewłaściwa, to mówimy, że całka niewłaściwa jest rozbieżnarozbieżna.

Rysunek 1: Interpretacja geometryczna całki niewłaściwej Riemanna I rodzaju w przedziale

W analogiczny sposób definuje się całkę niewłaściwą Riemanna I rodzaju funkcji określonej na przedziale

, jak również pojęcia jej zbieżności i rozbieżności. Przyjmujemy wówczas, że

[a, +∞)

(−∞, b]

[a, +∞)

(−∞, b]

f : [a, +∞) → R

[a, β]

a < β

f

f(x)dx

lim

β→+∞

∫

_a β

f(x)dx

∫

a +∞

f(x)dx

∫

_a+∞

f(x)dx

∫

_a+∞ [a, +∞)

f(x)dx

∫

b −∞

f

(−∞, b]

f(x)dx :=

f(x)dx.

∫

−∞ b

lim

α→−∞

∫

_α b (−∞, b]

(3)

Rysunek 2: Interpretacja geometryczna całki niewłaściwej Riemanna I rodzaju w przedziale

DEFINICJA

Definicja 2: Całka niewłaściwa Riemanna I rodzaju w zbiorze liczb rzeczywistych

Niech będzie funkcją całkowalną w sensie Riemanna w każdym przedziale domkniętym zawartym w .

Całkę niewłaściwą Riemanna I rodzaju

Całkę niewłaściwą Riemanna I rodzaju funkcji w definujemy jako

gdzie jest dowolnie wybranym punktem z . Jeżeli obie całki w powyższej sumie są zbieżne, to mówimy, że całka jest zbieżna. Gdy któraś z tych całek nie istnieje lub jest rozbieżna, to mówimy, że całka jest rozbieżna.

Należy podkreślić, że jeżeli całka jest zbieżna, to można wykazać, że jej wartość nie zależy od wyboru punktu w powyższej definicji.

PRZYKŁAD

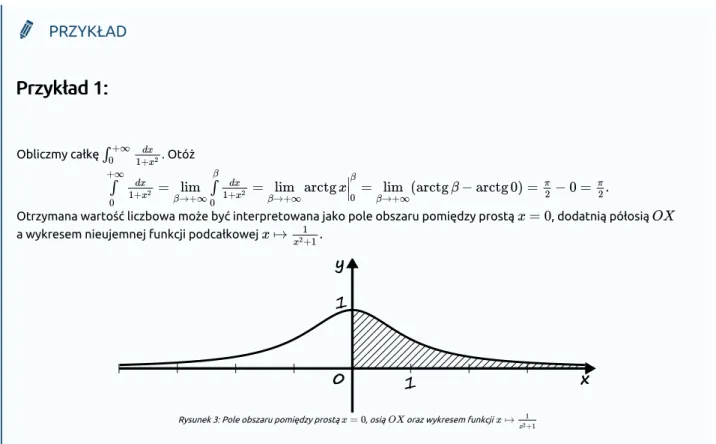
Przykład 1:

Obliczmy całkę . Otóż

Otrzymana wartość liczbowa może być interpretowana jako pole obszaru pomiędzy prostą , dodatnią półosią a wykresem nieujemnej funkcji podcałkowej

Rysunek 3: Pole obszaru pomiędzy prostą , osią oraz wykresem funkcji

Przykład ten pokazuje, że pole nieograniczonego obszaru na płaszczyźnie może być skończone. (−∞, b]

f : R → R

[α, β]

R

f R

f(x)dx :=

f(x)dx +

f(x)dx,

∫

−∞ +∞

∫

−∞ a

∫

a +∞

a

R

f(x)dx

∫

_−∞+∞

∫

_−∞+∞

f(x)dx

∫

+∞ −∞

a ∈ R

∫

₀+∞ dx 1+x2

=

arctg x =

(arctg β − arctg 0) = − 0 = .

∫

0 +∞ dx 1+x2

lim

β→+∞

∫

₀ β dx 1+x2

lim

β→+∞

∣∣

β 0 β→+∞

lim

π 2 π2

x = 0

OX

x ↦

1

.

+1 x2 x = 0 OX x ↦ 1 +1 x2

(4)

PRZYKŁAD

Przykład 2:

Przy ustalonej liczbie zbadajmy zbieżność całki w zależności od wartości parametru .

Przypadek 1. Przypadek 1. . Zauważmy, że a zatem Przypadek 2. Przypadek 2. .

Reasumując, całka jest zbieżna dla , a rozbieżna dla

Niewłaściwość całki ze względu na funkcję podcałkową (całka II rodzaju)

Sformułujmy teraz definicję całki niewłaściwej funkcji nieograniczonej określonej na przedziale ograniczonym.

a > 0

∫

+∞

dx

a x1p

p ∈ R

p ≠ 1

∫

a +∞

dx

x

p

=

∫

dx =

a +∞

x

−p

_lim

β→+∞

∫

a β

x

−p

_lim

β→+∞

x

−p+1

−p + 1

∣∣

β a

=

lim

=

(

−

).

β→+∞

1 (1 − p)x

p−1

∣∣

β a

1 1 − p lim

β→+∞

1 β

p−1

1 a

p−1

= {

lim

β→+∞ 1 βp−1

+∞,

0,

gdy p − 1 < 0,

gdy p − 1 > 0,

= {

∫

a +∞ dx xp

+∞,

,

1 (p−1)ap−1

gdy p < 1,

gdy p > 1.

p = 1

=

ln x =

(ln β − ln a) = +∞.

∫

a +∞ dx x _β→+∞

lim

∣∣

β a β→+∞

lim

(

∫

_a+∞ dx

)

xp

(p > 1)

(p ≤ 1).

(5)

DEFINICJA

Definicja 3: Całka niewłaściwa Riemanna II rodzaju w przedziale

lub

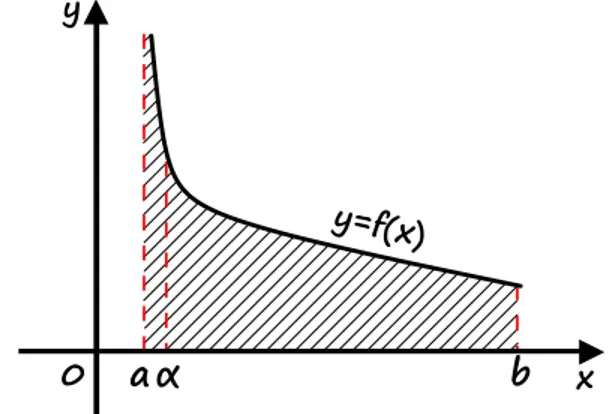
Niech będzie funkcją całkowalną w sensie Riemmana na każdym z przedziałów domkniętych , przy

czym . Załóżmy, że funkcja jest nieograniczona w pewnym lewostronnym sąsiedztwie punktu . CałkąCałką

niewłaściwą Riemanna II rodzaju

niewłaściwą Riemanna II rodzaju funkcji nazywamy granicę

i oznaczamy ją symbolem

Jeżeli powyższa granica istnieje i jest skończona, to mówimy, że całka niewłaściwa jest zbieżnazbieżna, natomiast jeżeli granica ta nie istnieje lub jest niewłaściwa, to mówimy, że całka niewłaściwa jest rozbieżnarozbieżna.

b

Rysunek 4: Interpretacja geometryczna całki niewłaściwej Riemanna II rodzaju w przedziale

W analogiczny sposób definiujemy całkę niewłaściwą Riemanna II rodzaju w przypadku, gdy funkcja jest

całkowalna w sensie Riemmana na każdym z przedziałów domkniętych , przy czym , oraz jest nieograniczona w

prawostronnym sąsiedztwie punktu . Wówczas przyjmujemy, że

W tej sytuacji analogicznie jak wyżej definiuje się pojęcia zbieżności i rozbieżności całki niewłaściwej.

Rysunek 5: Interpretacja geometryczna całki niewłaściwej Riemanna II rodzaju w przedziale

[a, b)

(a, b]

(f : [a, b) → R)

[a, β]

(a < β < b)

(f)

(b)

(f)

f(x)dx

lim

β→b−

∫

a β

f(x)dx.

∫

a b

f(x)dx

∫

b a

f(x)dx

∫

b a [a, b)

(f : (a, b] → R)

[α, b]

(a < α < b)

(a)

f(x)dx :=

f(x)dx.

∫

a b

lim

α→a+

∫

α b (a, b]

(6)

DEFINICJA

Definicja 4: Całka niewłaściwa Riemanna II rodzaju w przedziale

Niech będzie funkcją całkowalną w sensie Riemmana na każdym z przedziałów domkniętych , przy

czym . Załóżmy, że funkcja jest nieograniczona w pewnym prawostronnym sąsiedztwie punktu

oraz

w pewnym lewostronnym sąsiedztwie punktu . Całkę niewłaściwą Riemanna II rodzajuCałkę niewłaściwą Riemanna II rodzaju funkcji w definiujemy jako

gdzie jest dowolnie wybranym punktem z . Jeżeli obie całki po prawej stronie powyższej równości są zbieżne, to mówimy, że całka jest zbieżnazbieżna. Gdy któraś z tych całek nie istnieje lub jest rozbieżna, to mówimy, że całka niewłaściwa jest rozbieżnarozbieżna.

PRZYKŁAD

Przykład 3:

Obliczmy całkę . Zauważmy, że , a zatem funkcja podcałkowa jest nieograniczona

w lewostronnym sąsiedztwie punktu . Na początku znajdźmy następującą całkę nieoznaczoną:

Otrzymujemy zatem

a więc rozpatrywana całka niewłaściwa jest rozbieżna.

Obliczmy teraz całkę podobną do tej z przykładu 2, w którym przedział całkowania był nieograniczony. Po wykonaniu poniższych obliczeń warto porównać wyniki uzyskane w obu przykładach.

(a, b)

(f : (a, b) → R)

[α, β]

(a < α < β < b)

(f)

(a)

(b)

(f) (a, b)

f(x)dx = f(x)dx + f(x)dx,

∫

a b

∫

a c

∫

c b

(c)

((a, b))

( f(x)dx)

∫

b a

( f(x)dx)

∫

b a

(

∫

1

)

0 _(x−1)dx2

(

_x→1

lim

−_(x−1)1 2

= +∞)

(1)

∫

dx

=

= ∫ dt = − + C = −

+ C.

(x−1)2

∣

∣∣

t = x − 1

dt = dx

∣

∣∣

t12 1_t _x−11

=

( −

) =

(

− 1) = +∞,

∫

0 1 dx (x−1)2 _β→1

lim

−

∫

0 β dx (x−1)2 _β→1

lim

− x−11

∣∣

β 0 β→1

lim

− β−1−1

(7)

PRZYKŁAD

Przykład 4:

Przy ustalonej liczbie zbadajmy zbieżność całki w zależności od wartości parametru

Przypadek 1. Przypadek 1. . Zauważmy, że a zatem Przypadek 2. Przypadek 2. .

Reasumując, całka jest zbieżna dla , a rozbieżna dla .

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 15:52:58

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=dd0293bcc72e60906ac7ca6d12938e43