Podstawowe własności funkcji: okresowość, parzystość, nieparzystość, ograniczoność, monotoniczność

(1)

Podstawowe własności

funkcji: okresowość,

parzystość, nieparzystość,

ograniczoność, ...

Autorzy:

Anna Barbaszewska-Wiśniowska

2019

(2)

Podstawowe własności funkcji: okresowość, parzystość, nieparzystość, ograniczoność, monotoniczność

Autor: Anna Barbaszewska-Wiśniowska

DEFINICJA

Definicja 1: Funkcja okresowa

Funkcję nazywamy okresową, jeśli istnieje taka liczba , że dla każdego zachodzą warunki

oraz .

Liczbę nazywamy okresem funkcjiokresem funkcji. Jeżeli istnieje najmniejszy dodatnidodatni okres, to nazywamy go okresem podstawowymokresem podstawowym.

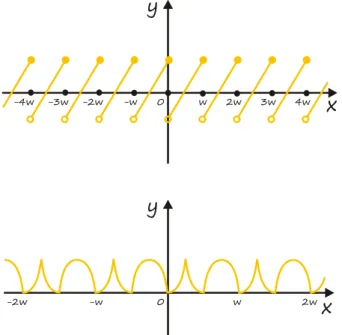
Rysunek 1: Przykłady funkcji okresowych

PRZYKŁAD

Przykład 1:

Okresem funkcji jest na przykład liczba . Jej okresem podstawowym jest liczba

PRZYKŁAD

Przykład 2:

Funkcja stała jest funkcją okresową, ale nie ma okresu podstawowego, bo każda liczba dodatnia może być jej okresem.

f : X → R

w ≠ 0

x ∈ X

x ± w ∈ X

f(x ± w) = f(x)

w

f(x) = sin x

4π

w = 2π

f(x) = c

(3)

UWAGA

Uwaga 1:

Jeżeli funkcja jest funkcja okresową o okresie , zaś , to funkcja oraz funkcja

mają ten sam okres, natomiast funkcja ma okres

Aby sporządzić wykres funkcji okresowej, wystarczy narysować go dla argumentów z dowolnego przedziału o długości , a następnie „powielić” na prawo i lewo od tego przedziału. Podobnie, aby podać funkcję okresową wystarczy zadać jej wartości w takim przedziale. Najbardziej znanymi funkcjami okresowymi są funkcje trygonometryczne. Okres podstawowy funkcji sinus i cosinus wynosi , zaś funkcji tangens i cotangens .

x ↦ f(x)

w

a ∈ R ∖ {0}

x ↦ f(x) + a

x ↦ af(x)

x ↦ f(ax)

w

|a|

w

(4)

ZADANIE

Zadanie 1:

Treść zadania: Treść zadania:

Które z funkcji , , są okresowe ? Wskaż, o ile istnieją, ich okresy podstawowe.

1. ,

2. ,

3. .

Rozwiązanie: Rozwiązanie:

Funkcja ma z góry zadany zbiór określoności, natomiast funkcje , będziemy rozpatrywać w ich dziedzinach naturalnych. Ad 1.

Ad 1.

Funkcja nie jest funkcja okresową, gdyż nie spełnia pierwszego warunku definicyjnego dotyczącego dziedziny. Jakkolwiek

próbowalibyśmy dobrać okres , to znajdziemy takie , że .

uwaga: gdyby funkcja ta była podana następująco to rozpatrywalibyśmy ją w jej dziedzinie naturalnej, (tzn. i oczywiście stwierdzilibyśmy, że jest to funkcja okresowa o okresie zasadniczym ).

Ad 2. Ad 2.

Dziedziną naturalną funkcji jest , gdyż wyrażenie ma sens dla dowolnej liczby rzeczywistej, więc pierwszy warunek definicyjny jest spełniony dla dowolnego . W związku z postacią funkcji (pamiętając, że funkcja

jest funkcją okresową o okresie zasadniczym ) stwierdzamy, że funkcja też jest okresowa. Jej okres zasadniczy wynosi .

Ad 3. Ad 3.

Podobnie jak dla funkcji pierwszy warunek definicyjny jest spełniony. Dalszą część zadania rozwiążemy graficznie,

korzystając z uwag dotyczących rysowania wykresów funkcji. Rysujemy etapami wykresy: , ,

Rysunek 2: Okresem zasadniczym funkcji jest

f g h

f :

R

−

→ R x → sin x

g : x ↦ cos 8x

h : x ↦ | sin x|

1 2

f

g h

f

w > 0

x ∈ R

−

x + w ∉ R

−

x ↦ sin x

R

2π

g

R

cos 8x

w > 0

g

x ↦ cos x

2π

g

=

2π 8 π4

g

x ↦ sin x x ↦ sin x

1 2

x ↦ | sin x|.

1 2 h 2π.

(5)

UWAGA

Uwaga 2:

Funkcje okresowe znajdują zastosowanie w technice do opisu zjawisk cyklicznych, np. drgań mechanicznych i akustycznych.

DEFINICJA

Definicja 2: Parzystość i nieparzystość funkcji

Funkcję

Funkcję nazywamy parzystąparzystą wtedy i tylko wtedy, gdy dla każdego liczba oraz .

Funkcję

Funkcję nazywamy nieparzystąnieparzystą wtedy i tylko wtedy, gdy dla każdego liczba oraz

.

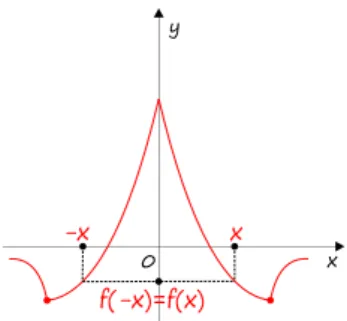
Rysunek 3: Funkcja parzysta. Wykres symetryczny względem osi

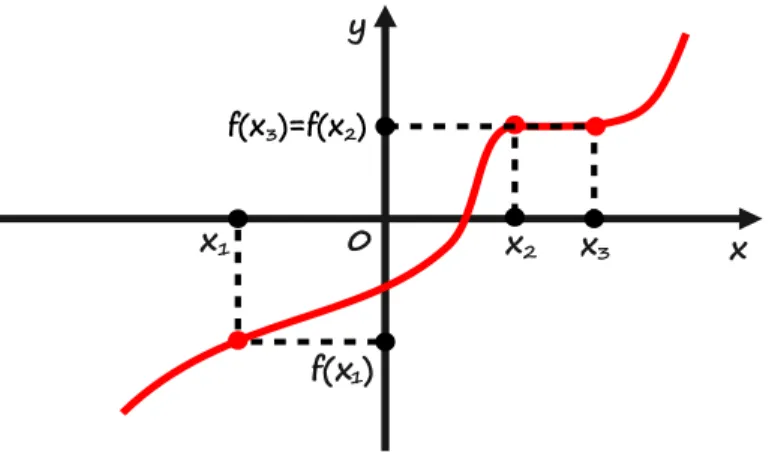
Rysunek 4: Funkcja nieparzysta. Wykres symetryczny względem punktu

UWAGA

Uwaga 3:

Warunek pierwszy wspólny dla funkcji parzystej i nieparzystej oznacza, że dziedzina każdej z nich powinna być symetryczna względem . W szczególności gdy , jest on trywialnie spełniony. Wykres funkcji parzystej jest symetryczny

względem osi , a nieparzystej względem początku układu współrzędnych czyli punktu .

f : X → Y

x ∈ X

(−x) ∈ X

f(−x) = f(x)

f : X → Y

x ∈ X

(−x) ∈ X

f(−x) = −f(x)

0y. (0, 0)

(0, 0)

X = R

0y

(0, 0)

(6)

UWAGA

Uwaga 4:

Spośród czterech podstawowych funkcji trygonometrycznych jedynie funkcja jest parzysta, pozostałe są

nieparzyste. Inne przykładowe funkcje parzyste, to , , , , a nieparzyste , .

Zauważmy, że większość funkcji nie ma ani własności parzystości, ani nieparzystości.

ZADANIE

Zadanie 2:

Zbadajmy parzystość i nieparzystość funkcji: .

Rozwiązując nierówność mamy .

Stąd . Jest to oczywiście przedział symetryczny względem punktu , czyli warunek pierwszy jest

spełniony. Obliczmy .

Odpowiedź Odpowiedź

Funkcja jest nieparzysta.

ZADANIE

Zadanie 3:

Zbadajmy parzystość i nieparzystość funkcji:

, więc warunek dotyczący symetrii dziedziny jest spełniony. Obliczając mamy

Funkcja jest parzysta.

x ↦ cos x

x ↦ x

2

_{x ↦ x}

4

_{x ↦ |x| x ↦}

_sin

2

_x

_{x ↦ x}

3

_{x ↦ x}

5

f : x ↦ log

₃5+x_5−x

= {x : 5 − x ≠ 0 ∧

> 0}.

D

f 5+x_5−x 5+x_5−x

> 0

x ∈ (−5, 5)

= (−5, 5)

D

f

(0, 0)

f(−x)

f(−x) =

log

35−x5+x

=

log

3

(

5+x5−x

)

= −

= −f(x).

−1

log

35+x5−x

f

g : x ↦ sin(cos 2x) + | sin x| + 4

= R

D

f

g(−x)

g

(7)

(1) (2)

TWIERDZENIE

Twierdzenie 1: O rozkładzie funkcji na parzystą i nieparzystą

Każdą funkcję o dziedzinie symetrycznej względem punktu można przedstawić w postaci sumy dwoch funkcji ,

z których pierwsza jest parzysta, a druga nieparzysta. Wówczas , .

PRZYKŁAD

Przykład 3:

Rozłożymy funkcję na sumy części parzystej i nieparzystej.

Rozwiązanie Rozwiązanie

jest zbiorem symetrycznym względem punktu , czyli taki rozkład jest możliwy. ,

. Odpowiedź

Odpowiedź

Część parzysta funkcji to funkcja kwadratowa , część nieparzysta funkcji to funkcja liniowa

PRZYKŁAD

Przykład 4:

Znajdziemy część parzystą i część nieparzystą funkcji .

Rozwiązanie Rozwiązanie

jest zbiorem symetrycznym względem , czyli taki rozkład jest możliwy. ,

.

Zauważmy, że tu . Wynika to z faktu, że dana funkcja jest funkcją nieparzystą. Wówczas jej częścią parzystą jest funkcja tożsamościowo równa zeru.

Część parzysta funkcji f to funkcja , część nieparzysta funkcji to funkcja .

f

(0, 0)

f

1

i

f

2

(x) =

f

1 f(x)+f(−x)₂

(x) =

f

2 f(x)−f(−x)₂

f(x) = 3 + 2x + 7

x

2

= R

D

f

(0, 0)

(x) =

=

= 3 + 7

f

1 f(x)+f(−x)₂ 3 +2x+7+(3(−x +2(−x)+7x 2 ₎2 2 6 +14x 2 2

x

2

(x) =

=

= 2x

f

2 f(x)−f(−x)₂ 3 +2x+7−(3(−x −2x+7)x 2 ₎2 2 3 +2x+7−3 +2x−7x 2 _x2 2 4x2

f

1

(x) = 3 + 7

x

2

f

(x) = 2x

f

2

f(x) = 2 sin(6x)

= R

D

f

(0, 0)

(x) =

=

= = 0

f

1 f(x)+f(−x)₂ 2 sin 6x+2 sin(−6x)₂ 2 sin 6x−2 sin 6x₂ 0₂

(x) =

=

= 2 sin 6x

f

2 f(x)−f(−x)₂ 2 sin 6x−2 sin(−6x)₂ 2 sin 6x+2 sin 6x₂

= f

f

2

f

(x) = 0

(8)

DEFINICJA

Definicja 3: Funkcja ograniczona z góry

Funkcja jest ograniczona z góry, jeżeli jej zbiór wartości jest ograniczony z góryograniczony z góry, czyli jeśli istnieje taka liczba , że dla każdego należacego do dziedizny funkcji

Rysunek 5: Funkcja ograniczona z góry. Wykres leży poniżej prostej

PRZYKŁAD

Przykład 5:

Funkcja jest ograniczona z góry. Jako można przyjąć liczbę lub każdą liczbę większą od . Nierówność

przyjmuje tu postać równoważną nierówności , która jest zawsze spełniona.

DEFINICJA

Definicja 4: Funkcja ograniczona z dołu

Funkcja jest ograniczona z dołu, jeżeli jej zbiór wartości jest ograniczony z dołuograniczony z dołu, czyli jeśli istnieje taka liczba ,

że dla każdego zachodzi

Rysunek 6: Funkcja ograniczona z dołu. Wykres leży nad prostą lub jej dotyka

f : X → Y

M

x

f(x) ≤ M.

y = M

f(x) = 3 − |x|

M

3

3 f(x) ≤ M

3 − |x| ≤ 3

|x| ≥ 0

f : X → Y

m

x ∈ D

f

f(x) ≥ m.

y = m

(9)

PRZYKŁAD

Przykład 6:

Funkcja jest ograniczona z dołu przez liczbę . Nierówność przyjmuje tu postać ,

czyli , co jest prawdą dla każdego .

PRZYKŁAD

Przykład 7:

Funkcja nie jest ograniczona ani z dołu, ani z góry, bo dla dowolnie dużego można wskazać takie , że

. Podobnie dla dowolnie małego można wskazać takie , że .

DEFINICJA

Definicja 5: Funkcja ograniczona

Funkcja

Funkcja jest ograniczonaograniczona, jeśli jest ona ograniczona zarówno z góry jak i z dołu.

Rysunek 7: Funkcja ograniczona. Wykres leży pomiedzy prostymi oraz

PRZYKŁAD

Przykład 8:

Funkcja jest ograniczona z góry przez liczbę i z dołu przez liczbę , czyli jest funkcją ograniczoną.

f(x) =

2

x

− 1

₋₁

_{f(x) ≥ m}

₂

x

_{− 1 ≥ −1}

≥ 0

2

x

_{x ∈ R.}

f(x) = x

3

_M

_x

> M

x

3

_m

_x

3

_{< m}

f : X → F

y = M y = −M

f(x) = 2 + cos x

3

1

(10)

DEFINICJA

Definicja 6: Funkcja rosnąca

Funkcja

Funkcja jest rosnąca w zbiorze rosnąca w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że .

Rysunek 8: Przykład funkcji rosnącej

DEFINICJA

Definicja 7: Funkcja słabo rosnąca

Funkcja

Funkcja jest słabo rosnąca (niemalejąca) w zbiorze słabo rosnąca (niemalejąca) w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że

Rysunek 9: Przykład funkcji słabo rosnącej

f

A ⊂ D

f

x

1

, ∈ A

x

2

x

1

<

x

2

f( ) < f( )

x

1

x

2

f

A ⊂ D

f

x

1

, ∈ A

x

2

<

(11)

UWAGA

Uwaga 5:

Jak wynika z powyższych definicji, funkcja rosnąca to taka funkcja, dla której wraz ze wzrostem argumentu wzrasta wartość funkcji. Wykres funkcji rosnącej ,,wznosi się od lewej do prawej.

DEFINICJA

Definicja 8: Funkcja malejąca

Funkcja

Funkcja jest malejąca w zbiorze malejąca w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że

Rysunek 10: Przykład funkcji malejącej

DEFINICJA

Definicja 9: Funkcja słabo malejąca

Funkcja

Funkcja jest słabo malejąca (nierosnąca) w zbiorze słabo malejąca (nierosnąca) w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że

f

A ⊂ D

f

x

1

, ∈ A

x

2

x

1

<

x

2

f( ) > f( )

x

1

x

2

f

A ⊂ D

f

x

1

, ∈ A

x

2

<

x

1

x

2

f( ) ≥ f( )

x

1

x

2

(12)

Rysunek 11: Przykład funkcji słabo malejącej

UWAGA

Uwaga 6:

Funkcja malejąca to taka funkcja, dla której wraz ze wzrostem argumentu maleje wartość funkcji. Wykres funkcji malejącej "opada w dół" od lewej do prawej.

DEFINICJA

Definicja 10: Funkcja monotoniczna

Funkcja monotoniczna w zbiorze

Funkcja monotoniczna w zbiorze to funkcja, która jest słabo rosnąca na lub słabo malejąca na .

Funkcję

Funkcję nazywamy ściśle monotoniczną w ściśle monotoniczną w , jeśli jest ona rosnąca lub malejąca.

UWAGA

Uwaga 7:

Monotoniczność funkcji ma duże znaczenie podczas rozwiązywania nierówności. Obrazowo można powiedzieć, że funkcje rosnące nie zmieniają zwrotu nierówności, natomiast funkcje malejące zmieniają ten zwrot.

Funkcje logartymiczne i wykładnicze o podstawie ułamkowej z przedziału są malejące, stąd zmiana zwrotu podczas "opuszczania" symbolu tych funkcji, np:

Rozwiązując nierówność:

pamiętamy, że funkcja jest malejąca i zmieniamy zwrot znaku nierówności przy "opuszczaniu logarytmu otrzymując nierówność kwadratową".

A ⊂ D

f

A

(0, 1)

(3x + 2) ≤

,

log

1 2

log

12

x

2

x ↦

log

1

x

2

3x + 2 ≥ x

2

(13)

Natomiast podczas rozwiązywania nierówności:

wiedząc, że funkcja jest rosnąca pozostawiamy niezmieniony zwrot nierówności otrzymując

wówczas nierówność kwadratową

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 10:06:02

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=80df4acfb034d2288fa20365a19148e2

Autor: Anna Barbaszewska-Wiśniowska

(3x + 2) ≤

,

log

2

log

2

x

2