Badanie przebiegu zmienności funkcji

(1)

Pochodna funkcji jednej

zmiennej rzeczywistej

Autorzy:

Tomasz Zabawa

Ilona Michalik

2019

(2)

Spis treści

Pochodna funkcji w punkcie. Pochodna jednostronna, niewłaściwa i funkcji odwrotnej Pochodna funkcji w przedziale. Różniczkowalność funkcji. Pochodna funkcji wektorowej Obliczanie pochodnej funkcji. Podstawowe wzory i twierdzenia

Pochodna funkcji a styczna do wykresu funkcji

Różniczka funkcji i jej zastosowanie do obliczeń przybliżonych Pochodne wyższych rzędów. Wzór Taylora

Zastosowanie pochodnej. Twierdzenie Rolle'a i Lagrange'a. Pochodna a monotoniczność funkcji Reguła de l'Hospitala

Ekstrema lokalne. Wartość najmniejsza i największa funkcji Wypukłość funkcji. Punkty przegięcia

(3)

Pochodna funkcji w punkcie. Pochodna jednostronna,

niewłaściwa i funkcji odwrotnej

Chcemy poznać prędkość obiektu, który porusza się ze zmienną prędkością. Mamy informację, jaką drogę przebył w każdym czasie między chwilą i . Obiekt przez pewien czas przyśpieszał, poruszał się ze stałą prędkością, zwalniał, zatrzymywał się,... Jeżeli policzymy iloraz drogi przebytej w czasie przez czas , to otrzymamy jedynie prędkość średnią, która słabo opisuje, jak poruszał się obiekt w rzeczywistości. Oczywiście możemy podzielić czas na mniejsze przedziały czasowe. Im mniejsze będą te przedziały czasowe, tym lepiej prędkość średnia przybliży nam rzeczywistą prędkość osiągniętą przez obiekt w tym krótszym czasie. Ideałem byłoby znać dokładną wartość prędkości w każdej chwili z osobna, czyli prędkość średnią zmierzoną przy długości przedziału czasu dążącej do zera.

I właśnie tak uzyskaną prędkość w danej chwili nazwiemy pochodną drogi względem czasu. Prędkość w danej chwili będzie zatem graniczną wartością prędkości średnich obliczonych w przedziale czasowym lub , o ile dąży do zera ( - inny moment czasu). Analogicznie możemy policzyć jak zmienia się inna wielkość w zależności od zmiany czasu i nie tylko, ponieważ pochodna opisuje, jak zmienia się wartość funkcji w stosunku do zmiany jej argumentu, gdy zmiana argumentu dąży do zera.

Zanim zdefiniujemy pochodną funkcji, określmy najpierw czym na osi liczbowej jest otoczenie punktu .

DEFINICJA

Definicja 1: Otoczenie punktu

Niech .

Otoczeniem punktu

Otoczeniem punktu o promieniu o promieniu nazywamy przedział i oznaczamy przez . Otoczeniem lewostronnym punktu

Otoczeniem lewostronnym punktu o promieniu o promieniu nazywamy przedział i oznaczamy przez . Otoczeniem prawostronnym punktu

Otoczeniem prawostronnym punktu o promieniu o promieniu nazywamy przedział i oznaczamy przez . Gdy promień otoczenia nie jest istotny (czyli może być dowolną liczbą dodatnią), powyższe otoczenia oznaczamy

odpowiednio przez , , .

Przejdźmy do definicji pochodnej funkcji jednej zmiennej w punkcie.

DEFINICJA

Definicja 2: Pochodna funkcji w punkcie

Niech oraz funkcja będzie określona w otoczeniu . Pochodną (właściwą) funkcji

Pochodną (właściwą) funkcji w punkcie w punkcie nazywamy granicę właściwą

Pochodną funkcji w punkcie oznaczamy przez lub też przez: , , .

Zatem

0 T

T

t

0

[ , t]

t

0

[t, ]

t

0

Δt = t − t

0

t

∈ R

x

0

∈ R

x

0

x

0

ε > 0

( − ε, + ε)

x

0

x

0

O( , ε)

x

0

x

0

ε > 0

( − ε, ]

x

0

x

0

O( , ε)

x

−0

x

0

ε > 0

[ , + ε)

x

0

x

0

O( , ε)

x

+0

O( )

x

0

O( )

x

−0

O( )

x

+0

∈ R

x

0

f

O( )

x

0

f

x

0

.

lim

x→x0 f(x)−f( )x0 x−x0

f

x

0

f

′

( )

x

0 dxdf

( )

x

0

f˙ x

( )

0

Df( )

x

0

( ) =

.

f

′

_x

₀

_lim

x→x0 f(x)−f( )x0 x−x0

(4)

UWAGA

Uwaga 1:

Podstawiając , otrzymujemy powyższą granicę w następującej postaci:

Zauważmy, że w tym zapisie oznacza przyrost argumentu. Ta postać czasem jest wygodniejsza przy obliczaniu pochodnej wprost z definicji.

PRZYKŁAD

Przykład 1:

Niech będzie funkcją drogi przebytej w czasie , gdzie . Niech , . Zatem

(jeżeli granica istnieje i jest właściwa) jest prędkością chwilową w chwili .

PRZYKŁAD

Przykład 2:

Korzystając z , obliczmy pochodną funkcji w punkcie oraz w dowolnym punkcie . Pochodna funkcji w punkcie :

Pochodna funkcji w dowolnie ustalonym punkcie :

PRZYKŁAD

Przykład 3:

Obliczmy pochodną funkcji w dowolnym punkcie .

(Wykonujemy podstawienie zatem i oraz przy .)

h = x − x

0

( ) =

.

f

′

_x

₀

_lim

h→0 f( +h)−f( )x0 x0 h

h

s = s(t)

s

t

t ∈ ( , )

T

1

T

2

t

0

, t ∈ ( , )

T

1

T

2

Δt = t − t

0

( ) =

s

′

_t

₀

_lim

Δt→0 s( +Δt)−s( )t0 t0 Δt

t

0

f(x) = x

2

_x

₀

_{= 2}

_x

₀

_{∈ R}

f

x

0

= 2

(2)

f

′

₌

_lim

₌

h→0

f(2 + h) − f(2)

h

lim

h→0

(2 + h −

)

2

₂

2

h

lim

h→0

4 + 4h + − 4

h

2

h

=

lim

=

(4 + h) = 4.

h→0

h(4 + h)

h

lim

h→0

f

x

0

( )

f

′

_x

₀

₌

_lim

₌

h→0

f( + h) − f( )

x

0

x

0

h

lim

h→0

( + h −

x

0

)

2

x

20

h

=

lim

=

h→0

+ 2 h + −

x

2 0

x

0

h

2

x

20

h

lim

h→0

h(2 + h)

x

0

h

=

lim

(2 + h) = 2 .

h→0

x

0

x

0

g(x) = e

x

_x

₀

_{∈ R}

( ) =

=

g

′

_x

₀

_lim

h→0 g( +h)−g( )x0 x0 h

lim

_h→0e − +h x0 ex0 h

lim

_h→0e ( −1) x0 eh h

t =

e

h

− 1,

_{t + 1 = e}

h

_{h = ln(t + 1)}

_{t =}

_e

h

_{− 1 → 0}

_{h → 0}

=

lim

=

.

t→0 t ex0 ln(t+1)

lim

_t→0 1ln(t+1)ex0 t

lim

t→0 ex0 ln(t+1)1t ex0 ln e

e

x0

(5)

PRZYKŁAD

Przykład 4:

Obliczmy pochodną funkcji w punkcie .

Z teorii granicy funkcji wiemy, że ta granica (obustronna) nie istnieje, ponieważ oraz

Skoro powyższa granica nie istnieje, to również pochodna funkcji w punkcie nie istnieje.

Pochodna funkcji w punkcie jest granicą (obustronną). Oprócz granicy (obustronnej) funkcji rozważamy również granice jednostronne funkcji. W związku z tym, definiujemy również pochodne jednostronne funkcji w punkcie .

DEFINICJA

Definicja 3: Pochodna lewostronna funkcji w punkcie

Niech oraz funkcja będzie określona w otoczeniu .

Pochodną lewostronną (właściwą) funkcji

Pochodną lewostronną (właściwą) funkcji w punkcie w punkcie , którą oznaczamy przez , nazywamy granicę właściwą

DEFINICJA

Definicja 4: Pochodna prawostronna funkcji w punkcie

Niech oraz funkcja będzie określona w otoczeniu .

Pochodną prawostronną (właściwą) funkcji

Pochodną prawostronną (właściwą) funkcji w punkcie w punkcie , którą oznaczamy przez , nazywamy granicę właściwą

k(x) = |x − 3|

x

0

= 3

(3) =

=

.

k

′

_lim

h→0 k(3+h)−k(3) h

lim

_h→0|3+h−3|−|3−3|h

lim

_h→0|h|h

=

= −1

lim

h→0− |h| h _h→0

lim

−−hh

=

= 1.

lim

h→0+ |h| h _h→0

lim

+ h h

k

x

0

= 3

x

0

∈ R

x

0

f

O( )

x

−0

f

x

0

f

′−

( )

x

0

( ) =

=

.

f

′−

x

0 _x→x

lim

₋ 0 f(x)−f( )x0 x−x0 _h→0

lim

− f( +h)−f( )x0 x0 h

∈ R

x

0

f

O( )

x

+₀

f

x

0

f

+′

( )

x

0

( ) =

=

.

f

₊′

_x

₀

_lim

x→x+ 0 f(x)−f( )x0 x−x0 _h→0

lim

+ f( +h)−f( )x0 x0 h

(6)

PRZYKŁAD

Przykład 5:

Wróćmy do : pokazaliśmy, że pochodna funkcji w punkcie nie istnieje. Obliczmy pochodne jednostronne funkcji w punkcie :

Zatem funkcja nie ma pochodnej w punkcie , ale ma pochodne jednostronne w tym punkcie, które są różne.

TWIERDZENIE

Twierdzenie 1: Warunek konieczny i wystarczający istnienia pochodnej funkcji w

punkcie

Niech oraz funkcja będzie określona w otoczeniu . Funkcja ma pochodną w punkcie wtedy i tylko wtedy, gdy

Jeżeli pochodne jednostronne w punkcie są równe, to ich wspólna wartość jest równa pochodnej (obustronnej) w punkcie .

Przyjrzyjmy się jeszcze twierdzeniu o pochodnej funkcji odwrotnej w punkcie i zobaczmy zastosowanie tego twierdzenia do obliczenia pochodnej funkcji arcus sinus w dowolnie zadanym punkcie .

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: o pochodnej funkcji odwrotnej

o pochodnej funkcji odwrotnej

Jeżeli funkcja jest ciągła i ściśle monotoniczna w otoczeniu i ma pochodną właściwą , to

gdzie , czyli .

k(x) = |x − 3|

x

0

= 3

k

x

0

= 3

(3)

k

′−

=

lim

=

h→0−

k(3 + h) − k(3)

h

h→0

lim

−

|3 + h − 3| − |3 − 3|

h

h→0

lim

−

|h|

h

=

lim

= −1,

h→0−

−h

h

(3)

k

′ +

=

_h→0

lim

+

=

k(3 + h) − k(3)

h

h→0

lim

+

|3 + h − 3| − |3 − 3|

h

h→0

lim

+

|h|

h

=

lim

= 1.

h→0+

h

k

x

0

= 3

∈ R

x

0

f

O( )

x

0

f

x

0

f

′−

( ) = ( ).

x

0

f

+′

x

0

x

0

x

0

x

0

∈ (−1, 1)

x

0

f

O( )

x

0

f

′

( ) ≠ 0

x

0

(

f

−1

₎

′

( ) =

_y

₀ 1

,

( ) f′_x 0

= f( )

y

0

x

0

x

0

=

f

−1

( )

y

0

(7)

PRZYKŁAD

Przykład 6:

Niech . Obliczmy pochodną funkcji w punkcie , jeżeli wiadomo, że dla dowolnego

. Funkcja określona w przedziale jest funkcją odwrotną do funkcji zawężonej do przedziału . Zauważmy, że funkcja jest ciągła i silnie rosnąca w przedziale oraz jej pochodna istnieje i jest

różna od zera dla każdego , bo dla każdego . Zatem założenia są spełnione. Na mocy

istnieje pochodną funkcji w punkcie i wynosi

stąd pamiętając, że , bo , otrzymujemy

Z własności funkcji odwrotnej wiemy, że dla każdego , więc

Jeżeli mówimy o pochodnej funkcji w punkcie , to mówimy o pochodnej właściwej funkcji w punkcie , ale możemy również zdefiniować rzadziej rozważaną pochodną niewłaściwą funkcji w punkcie .

DEFINICJA

Definicja 5: Pochodna niewłaściwa funkcji w punkcie

Niech oraz funkcja będzie określona i ciągła w otoczeniu . Mówimy, że funkcja funkcja ma pochodną niewłaściwą w punkcie ma pochodną niewłaściwą w punkcie , gdy Fakt, że funkcja ma pochodną niewłaściwą w punkcie zapisujemy:

Definiuje się również jednostronne pochodne niewłaściwe funkcji w punkcie .

DEFINICJA

Definicja 6: Pochodna niewłaściwa lewostronna funkcji w punkcie

Niech oraz funkcja będzie określona i ciągła w otoczeniu .

Mówimy, że funkcja funkcja ma pochodną niewłaściwą lewostronną w punkcie ma pochodną niewłaściwą lewostronną w punkcie , gdy

co zapisujemy: lub .

∈ (−1, 1)

x

0

arcsin

x

0

(sin x = cos x

)

′

x ∈ R

arcsin

(−1, 1)

sin

(− , )

π 2 π2

sin |

(− , )π 2 π2

(− , )

π 2 π2

x ∈ (− , )

π 2 π2

cos x > 0

x ∈ (− , )

π2 π2

arcsin

x

0

(arcsin

x

0

)

′

=

_{cos y0}1

, gdzie = arcsin ,

y

0

x

0

cos > 0

y

0

y

0

∈ (− , )

π₂ π₂

(arcsin

x

0

)

′

=

_{cos y0}1

=

1

=

1−sin2( )_y 0 √ 1 1−sin2(arcsin x) √

sin(arcsinx) = x

x ∈ [−1, 1]

=

1

.

1−x2 √

x

0

x

0

x

0

∈ R

x

0

f

O( )

x

0

f

x

0

= −∞ lub

= +∞.

lim

x→x0 f(x)−f( )x0 x−x0 _x→x

lim

₀ f(x)−f( )x0 x−x0

x

0

( ) = −∞ lub

( ) = +∞.

f

′

_x

₀

_f

′

_x

₀

f

x

0

∈ R

x

0

f

O( )

x

−0

f

x

0

= −∞ lub

= +∞,

lim

x→x−₀ f(x)−f( )x0 x−x0 _x→x

lim

−₀ f(x)−f( )x0 x−x0

( ) = −∞

f

′−

x

0

f

′−

( ) = +∞

x

0

(8)

DEFINICJA

Definicja 7: Pochodna niewłaściwa prawostronna funkcji w punkcie

Niech oraz funkcja będzie określona i ciągła w otoczeniu .

Mówimy, że funkcja funkcja ma pochodną niewłaściwą prawostronną w punkcie ma pochodną niewłaściwą prawostronną w punkcie , gdy

co zapisujemy: lub .

Pochodna funkcji w przedziale. Różniczkowalność

funkcji. Pochodna funkcji wektorowej

Pojęcie pochodnej funkcji w punkcie możemy rozszerzyć na przedział i mówić o pochodnej funkcji w przedziale. Z pochodną funkcji wiąże się również pojęcie różniczkowalności funkcji.

DEFINICJA

Definicja 8: Pochodna funkcji w przedziale

Mówimy, że funkcja funkcja ma pochodną w przedziale otwartym ma pochodną w przedziale otwartym , gdzie , gdy funkcja ma pochodną w każdym punkcie tego przedziału.

Mówimy, że funkcja funkcja ma pochodną w przedziale domkniętym ma pochodną w przedziale domkniętym , gdzie , gdy funkcja ma pochodną w przedziale otwartym i pochodną prawostronną w i pochodną lewostronną w .

Mówimy, że funkcja funkcja ma pochodną w przedziale ma pochodną w przedziale , gdzie , gdy funkcja ma pochodną w przedziale otwartym i pochodną lewostronną w .

Mówimy, że funkcja funkcja ma pochodną w przedziale ma pochodną w przedziale , gdzie , gdy funkcja ma pochodną w przedziale otwartym i pochodną prawostronną w .

Definiuje się również następujące pojęcia:

DEFINICJA

Definicja 9: Funkcja pochodna

Funkcję określoną w przedziale , której wartości są równe dla każdego , nazywamy funkcją pochodną funkcji funkcją pochodną funkcji w przedziale

w przedziale lub pochodną funkcji pochodną funkcji w przedziale w przedziale i oznaczamy ją przez lub .

∈ R

x

0

f

O( )

x

+0

f

x

0

= −∞ lub

= +∞,

lim

x→x+ 0 f(x)−f( )x0 x−x0 _x→x

lim

+ 0 f(x)−f( )x0 x−x0

( ) = −∞

f

′ +

x

0

f

+′

( ) = +∞

x

0

f

(a, b)

−∞ ≤ a < b ≤ ∞

f

[a, b]

−∞ < a < b < ∞

f

(a, b)

a

b

f

(a, b]

−∞ ≤ a < b < ∞

f

(a, b)

b

f

[a, b)

−∞ < a < b ≤ ∞

f

(a, b)

a

I

f

′

(x)

_{x ∈ I}

_f

I

f

I

f

′ df dx

(9)

DEFINICJA

Definicja 10: Funkcja różniczkowalna

Funkcję mającą pochodną (właściwą) w każdym punkcie przedziału nazywamy funkcją różniczkowalnąfunkcją różniczkowalną w tym przedziale. Przyglądnijmy się teraz klasie funkcji różniczkowalnych - sformułujemy dwa twierdzenia opisujące własności funkcji różniczkowalnych.

TWIERDZENIE

Twierdzenie 3: o ciągłości funkcji różniczkowalnej

Jeżeli funkcja ma pochodną właściwą w punkcie , to jest ciągła w punkcie .

UWAGA

Uwaga 2:

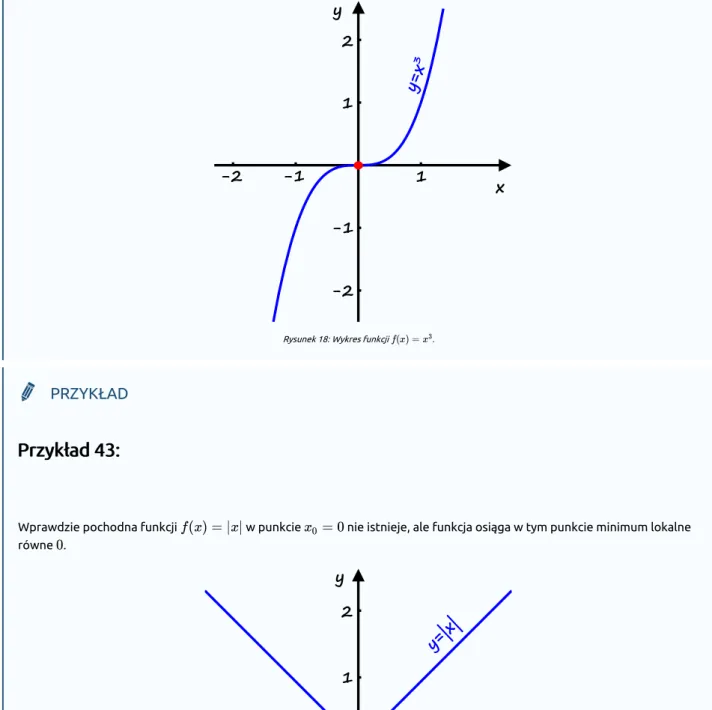
Implikacja w przeciwnym kierunku nie jest prawdziwa, czyli nie każda funkcja ciągła musi być różniczkowalna. Świadczy o tym przykład funkcji ciągłej , która nie posiada pochodnej w . Zbiór funkcji różniczkowalnych jest zatem podzbiorem funkcji ciągłych i jest to podzbiór właściwy.

TWIERDZENIE

Twierdzenie 4:

Twierdzenie 4: o pochodnej funkcji elementarnej

o pochodnej funkcji elementarnej

Jeżeli pochodna funkcji elementarnej istnieje, to jest ona funkcją elementarną.

UWAGA

Uwaga 3:

Funkcja elementarna to funkcja, którą można otrzymać z podstawowych funkcji elementarnych za pomocą skończonej liczby działań arytmetycznych oraz operacji składania i odwracania funkcji. Zatem funkcję elementarną możemy zapisać za pomocą jednego wzoru wykorzystując tylko podstawowe funkcje elementarne.

mówi, że pochodną takiej funkcji zawsze możemy zapisać jednym wzorem. Jest to istotna wiadomość i nie jest to własność oczywista - np. całka nieoznaczona (będąca operacją odwrotną do pochodnej) nie ma tej własności.

Zdefiniujmy również pochodną funkcji wektorowej.

x

0

x

0

(10)

DEFINICJA

Definicja 11: Pochodna funkcji wektorowej

Niech o przepisie będzie funkcją wektorową.

Pochodną funkcji wektorowej

Pochodną funkcji wektorowej określamy wzorem

UWAGA

Uwaga 4:

Analogicznie określamy pochodną funkcji wektorowej o przepisie :

Obliczanie pochodnej funkcji. Podstawowe wzory i

twierdzenia

Pochodną funkcji można obliczyć, korzystając z twierdzeń opisujących własności pochodnych funkcji - i - oraz . Poniżej przedstawimy te twierdzenia oraz przykłady obliczania pochodnej funkcji wykorzystujące te własności.

: [α, β] →

v⃗

R

2

_v⃗

_{(t) = (x(t), y(t))}

v⃗

(t) = ( (t), (t)).

v⃗

′

_x

′

_y

′

: [α, β] →

v⃗

R

3

_v⃗

_{(t) = (x(t), y(t), z(t))}

(t) = ( (t), (t), (t)).

v⃗

′

_x

′

_y

′

_z

′

(11)

TWIERDZENIE

Twierdzenie 5:

Twierdzenie 5: Wzory na pochodne podstawowych funkcji

Wzory na pochodne podstawowych funkcji

Pochodne funkcji względem zmiennej wyrażają się wzorami:

Pochodna funkcji stałej: Pochodna funkcji stałej:

, gdzie jest stałą Pochodna funkcji potęgowej: Pochodna funkcji potęgowej:

, gdzie jest stałą

Pochodna funkcji wykładniczej i logarytmicznej: Pochodna funkcji wykładniczej i logarytmicznej:

, gdzie jest stałą

Pochodna funkcji trygonometrycznych: Pochodna funkcji trygonometrycznych:

Pochodna funkcji cyklometrycznych: Pochodna funkcji cyklometrycznych:

Jako zakres zmiennej dla powyższych wzorów przyjmujemy część wspólną dziedziny funkcji pod znakiem pochodnej i dziedziny funkcji po prawej stronie znaku równości.

UWAGA

Uwaga 5:

Wszystkie powyższe wzory są wyprowadzone z w dowolnym punkcie lub przy użyciu .

x

(c = 0

)

′

_{c ∈ R}

(

x

a

₎

′

= a

_x

a−1

_{a ∈ R}

(

a

x

₎

′

= ln a

_a

x

_{a ∈ (0, 1) ∪ (1, ∞)}

(

e

x

₎

′

=

_e

x

(

log

a

x =

)

′ x ln a1

a ∈ (0, 1) ∪ (1, ∞)

(ln x =

)

′ 1 x

(sin x = cos x

)

′

(cos x = − sin x

)

′

(tg x =

)

′ 1 x cos2

(ctg x = −

)

′ 1 x sin2

(arcsinx =

)

′ 1 1−x2 √

(arccosx = −

)

′ 1 1−x2 √

(arctgx =

)

′ 1 +1 x2

(arcctgx = −

)

′ 1 +1 x2

x

(12)

PRZYKŁAD

Przykład 7:

Obliczymy pochodną funkcji z definicji.

Pochodną funkcji można obliczyć z definicji, jednak często jest to żmudne zadanie. Dlatego zazwyczaj obliczamy pochodną funkcji, wykorzystując i oraz powyższe .

TWIERDZENIE

Twierdzenie 6:

Twierdzenie 6: o pochodnej operacji algebraicznych

o pochodnej operacji algebraicznych

Jeżeli funkcje i mają pochodne właściwe w punkcie ,

to

UWAGA

Uwaga 6:

Powyższe wzory są również prawdziwe dla pochodnych jednostronnych.

f(x) = sin x

(x) =

f

′

=

lim

h→0

f(x + h) − f(x)

h

lim

h→0

sin(x + h) − sin(x)

h

=

lim

h→0

sin xcos h + cos xsin h − sin x

h

=

lim

h→0

sin x(1 − 2

sin

2 h

) + cos xsin h − sin x

2

h

=

lim

h→0

−2 sin x

sin

2 h

+ cos xsin h

2

h

(−2 sin x

+ cos x

) =

lim

h→0

sin

2 h 2

h

sin h

h

(− sin x ⋅ sin ⋅

+ cos x ⋅

) =

lim

h→0

h

2 sin

h 2 h 2

sin h

h

− sin x ⋅ 0 ⋅ 1 + cos x ⋅ 1 = cos x.

f g

x

0

(k ⋅ f ( ) =

)

′

_x

₀

(f + g ( ) =

)

′

_x

0

(f − g ( ) =

)

′

_x

0

(f ⋅ g ( ) =

)

′

_x

0

( ) =

( )

f

_g

′

x

0

k ⋅ ( ), gdzie k jest sta

f

′

_x

₀ łą

,

( ) + ( ),

f

′

_x

0

g

′

x

0

( ) − ( ),

f

′

_x

0

g

′

x

0

( )g( ) + f( ) ( ),

f

′

_x

0

x

0

x

0

g

′

x

0

.

( )g( ) − f( ) ( )

f

′

_x

₀

_x

₀

_x

₀

_g

′

_x

₀

[g( )

x

0

]

2

(13)

PRZYKŁAD

Przykład 8:

Obliczmy pochodną funkcji:

Wykorzystując wzory na pochodną sumy i różnicy otrzymujemy: Ze wzorów na pochodną iloczynu stałej i funkcji:

Teraz pod znakiem pochodnej mamy jedynie funkcje potęgowe i funkcję stałą, których pochodne znamy, zatem:

PRZYKŁAD

Przykład 9:

Wykorzystując powyższe twierdzenie, obliczmy pochodne funkcji:

Pochodna funkcji została policzona, ale uprośćmy jeszcze ten przepis:

Przy liczeniu pochodnej funkcji elementarnej będziemy często potrzebować jeszcze wzoru na pochodną złożenia funkcji.

TWIERDZENIE

Twierdzenie 7:

Twierdzenie 7: o pochodnej funkcji złożonej

o pochodnej funkcji złożonej

Jeżeli funkcja ma pochodną właściwą w punkcie i funkcja ma pochodną właściwą w punkcie , to

UWAGA

Uwaga 7:

Powyższy wzór jest prawdziwy dla funkcji będącej złożeniem dowolnej skończonej liczby funkcji, a także dla pochodnych jednostronnych.

f(x) = 2 + 4 − 3.

x

2

_x

5

(x) = (2

+ (4

− (3 =

f

′

_x

2

₎

′

_x

5

₎

′

₎

′

= 2(

x

2

₎

′

+ 4(

_x

5

₎

′

− (3 =

₎

′

= 2 ⋅ 2x + 4 ⋅ 5 − 0 = 4x + 20 .

x

4

_x

4

g(x) =

x

3

sin x,

h(x) =

ln x

.

ctg x

(x) = ( sin x = (

sin x + (sin x = 3 sin x + cos x

g

′

_x

3

₎

′

_x

3

₎

′

_x

3

₎

′

_x

2

_x

3

(x) =

=

h

′ ln x ctg x (ln x ctg x−ln x(ctg x) ′ ₎′ x ctg2 ctg x−ln x(− ) 1 x _sin21_x x ctg2

h

=

ctg x_x_sinsin22_xx+x ln x_ctg2_x

=

sin x cos x+x ln x_x_cos2_x

.

f

x

0

g

f( )

x

0

(g ∘ f ( ) = ( )

)

′

_x

₀

_g

′

_y

₀

_|

⋅ ( ).

=f( )

(14)

UWAGA

Uwaga 8:

Wyrażenie w powyższym wzorze oznacza, że najpierw liczymy pochodną funkcji zewnętrznej , a dopiero następnie w miejsce zmiennej wstawiamy funkcję wewnętrzną .

PRZYKŁAD

Przykład 10:

Obliczmy pochodne funkcji:

Funkcja jest złożeniem dwóch funkcji. Funkcją wewnętrzną jest funkcja , natomiast funkcją zewnętrzną jest . Zauważmy, że , czyli tym razem funkcja sinus jest funkcją wewnętrzną.

PRZYKŁAD

Przykład 11:

Funkcja, której liczymy pochodną, może być złożeniem większej ilości funkcji, tak jak: Jest to złożenie trzech funkcji. Wtedy

UWAGA

Uwaga 9:

Zauważmy, że licząc pochodną funkcji złożonej, wygodnie jest liczyć pochodną rozpoczynając od pochodnej funkcji najbardziej zewnętrznej. Podobnie jeżeli funkcja ma rozbudowany wzór, to wygodnie jest rozpocząć liczenie pochodnej od operacji najbardziej zewnętrznej, niezależnie czy jest to operacja złożenia funkcji, czy operacja będąca działaniem

arytmetycznym na funkcjach. Jeżeli mamy problem z określeniem, która operacja jest najbardziej zewnętrzna, to przyjrzyjmy się kolejności wykonywanych operacji, gdy za podstawimy dowolną liczbę z dziedziny. Operacja, którą wykonujemy jako ostatnią, będzie operacją najbardziej zewnętrzną.

(y)

g

′

_|

y=f(x)

g

y

f(x)

(x) = sin 4x,

(x) =

x.

f

1

f

2

sin

4

f

1

4x

sin y

(x) = (sin 4x = (sin y

⋅ (4x = (cos y)

⋅ 4 = cos 4x ⋅ 4 = 4 cos 4x.

f

′

1

)

′

)

′

|

y=4x

)

′

|

y=4x

x = (sin x

sin

4

₎

4

(x) = ((sin x

= (

⋅ (sin x = (4 )

⋅ cos x = 4

x ⋅ cos x.

f

′

2

)

4

)

′

y

4

)

′

|

y=sin x

)

′

y

3

|

y=sin x

sin

3

(x) =

3x.

f

3

sin

5

(x) =

f

′ 3

=

(

sin

5

3x = ((sin 3x

₎

′

₎

5

₎

′

= (

_y

5

₎

′

_|

⋅ (sin 3x =

y=sin 3x

)

′

5(sin 3x ⋅ (sin 3x = 5(sin 3x ⋅ (sin y

)

4

₎

′

₎

4

₎

′

_|

⋅ (3x =

y=3x

)

′

5(sin 3x ⋅ cos 3x ⋅ 3 = 15

)

4

_sin

4

3xcos 3x.

(15)

PRZYKŁAD

Przykład 12:

Obliczmy pochodne funkcji: w ich dziedzinach.

Dla dowolnego należącego do dziedziny funkcji :

(x) = ln(

+ 4 ),

(x) =

g

1

3

5x+4x3

x

7

g

2 log cos x 4 5x_x5

x

g

1

(x) =

g

′ 1

=

(ln(

3

5x+4x3

+ 4 ) =

⋅ (

+ 4

=

x

7

₎

′

1 + 4

3

5x+4x3

x

7

3

5x+4x3

x

7

₎

′

⋅ ((

+ (4

) =

1 + 4

3

5x+4x3

x

7

3

5x+4x3

)

′

_x

7

₎

′

(

ln 3 ⋅ (5x + 4

+ 28 ) =

1 + 4

3

5x+4x3

x

7

3

5x+4x3

x

3

₎

′

_x

6

(

ln 3 ⋅ (5 + 12 ) + 28 ) =

1 + 4

3

5x+4x3

x

7

3

5x+4x3

x

2

_x

6

.

(5 + 12 ) ln 3 + 28

3

5x+4x3

x

2

_x

6

+ 4

3

5x+4x3

x

7

x

g

2

(x) =

g

′ 2

=

(

log

₅

4_x

cos x

)

x

5

′

₍

_log

₄

_{cos x}

₎

_′

₅

_x

₅

_{− (}

_log

₄

_{cos x)(}

₅

_x

₅

₎

_′

(5

x

_x

5

₎

2

=

4 log

3

cos x(log cos x

₎

′

₅

x

_x

5

− (

_log

4

cos x) ((

₅

x

₎

′

_x

5

+ (

₅

x

_x

5

₎

′

)

25

x

_x

10

=

4 log

3

cos x ⋅

1

(cos x

− (

cos x)( ln 5 ⋅ + 5 )

cos x ln 10

)

′

5

x

5

log

4

5

x

5

x

4

25

x

_x

10

=

(− sin x)

− (

cos x)( ln 5 ⋅ + 5 )

4log3cos x cos x ln 10

5

x

5

log

4

5

x

5

x

4

25

x

_x

10

.

− (

cos x)(

ln 5 + 5

)

−4tg xlog3cos x ln 10

5

x

5

log

4

x

5

x

4

5

x

25

x

_x

10

(16)

UWAGA

Uwaga 10:

Do obliczania pochodnych funkcji złożonych postaci wykorzystujemy przekształcenia:

Zauważmy, że przed przekształceniem funkcji nie możemy zastosować ani wzoru na pochodną funkcji potęgowej, ani na pochodną funkcji wykładniczej, bo zmienna występuje i w wykładniku, i w podstawie potęgi. Również wzór na pochodną funkcji logarytmicznej wymaga, aby podstawa logarytmu była liczbą. Aby móc zastosować znane wzory na pochodne, przekształcamy przepisy tych funkcji tak, aby w podstawie potęgi i w podstawie logarytmu były liczby. Wykorzystując złożenie funkcji odwrotnych do siebie (funkcja jest funkcją odwrotną do funkcji ), otrzymujemy:

Natomiast ze wzoru na zmianę podstawy logarytmu mamy:

PRZYKŁAD

Przykład 13:

Zobaczmy zastosowanie tych wzorów do obliczenia pochodnej następujących funkcji: oraz

Wykorzystując przekształcenie , możemy obliczyć pochodną funkcji :

W przypadku pochodnej funkcji wykorzystamy wzór :

UWAGA

Uwaga 11:

Jeżeli chcemy obliczyć pochodną funkcji w zadanym punkcie, np. w , wykorzystując wzory, to najpierw liczymy pochodną dla dowolnego z dziedziny, a następnie dopiero wartość obliczonej pochodnej dla zadanego argumentu .

(f(x)

)

g(x)

oraz

_log

g(x)

f(x)

(f(x)

)

g(x)

=

_e

g(x) ln f(x)

oraz

_log

g(x) =

.

f(x) _{ln f(x)}ln g(x)

(f(x))

g(x)

y = ln x

y = e

x

(f(x)

)

g(x)

=

₍

_e

ln f(x) g(x)

₎

=

_e

g(x) ln f(x)

.

g(x) =

.

log

f(x) ln g(x)_{ln f(x)}

(x) =

dla x ∈ (0, +∞)

f

1

x

(x) =

sin x dla x ∈ (0, 1).

f

2

log

x

(f(x)

)

g(x)

=

_e

g(x) ln f(x)

_f

₁

(x) =

=

(xln x =

(1 ⋅ ln x + x ⋅ ) = (1 + ln x).

f

′ 1

( )

x

x ′

(

e

x ln x ′

)

e

x ln x

)

′

e

x ln x x1

x

f

2

log

f(x)

g(x) =

_{ln f(x)}ln g(x)

(x) =

f

′ 2

=

(

log

x

sin x =

)

′

(

ln sin x

_{ln x}

)

=

′

_{(ln sin x ln x − ln sin x(ln x}

₎

′

₎

′

x

ln

2

=

.

⋅ cos x ⋅ ln x − ln sin x ⋅

1 sin x x1

x

ln

2

ctg x ⋅ ln x −

ln sin x x

x

ln

2

= 2

x

0

x

0

(17)

PRZYKŁAD

Przykład 14:

Obliczymy , jeżeli .

Najpierw obliczamy pochodną funkcji dla dowolnego (w sposób podobny jak w poprzednim przykładzie):

a następnie

Pochodna funkcji a styczna do wykresu funkcji

Pojęcie stycznej do wykresu funkcji w danym punkcie wykresu jest ściśle związane z pochodną funkcji w punkcie . Styczną możemy traktować jako geometryczną interpretację pochodnej funkcji.

Pojęcie stycznej w sensie rachunku różniczkowego jest czymś innym niż styczna do figury czyli prosta mająca dokładnie jeden punkt wspólny z figurą, którą poznaje się w szkole średniej.

DEFINICJA

Definicja 12: Styczna do wykresu funkcji

Niech oraz funkcja będzie określona i ciągła w otoczeniu . Styczną do wykresu funkcji

Styczną do wykresu funkcji w punkcie w punkcie (w punkcie wykresu (w punkcie wykresu lub dla argumentu lub dla argumentu )) nazywamy prostą będąca granicznym położeniem siecznych wykresu funkcji przechodzących przez punkty i , gdy

.

f(x

₀

)

y=f

(x)

Rysunek 1: Styczna do wykresu funkcji w punkcie jako graniczne położenie siecznych, gdy .

(2)

f

′

_{f(x) = (3x)}

x2

f

x > 0

(x) =

f

′

=

((3x )

)

x2 ′

(

e

x2ln(3x)

)

′

e

x2ln(3x)

( ln(3x))

x

2 ′

(2x ⋅ ln(3x) + ⋅

) = (3x (x + 2xln(3x)) ,

e

x2ln(3x)

x

2

3 3x

)

x 2

(2) = (3 ⋅ 2 (2 + 2 ⋅ 2 ln(3 ⋅ 2)) = (2 + 4 ln 6) = 1296(2 + 4 ln 6).

f

′

₎

22

6

4

f

P( , f( ))

x

0

x

0

f

x

0

∈ R

x

0

f

O( )

x

0

f

x

0

P( , f( ))

x

0

x

0

x

0

f

( , f( ))

x

0

x

0

(x, f(x))

x → x

0 x0 x → x0

(18)

UWAGA

Uwaga 12:

Współczynnik kierunkowy siecznej przechodzącej przez punkty i jest dany wzorem

st

yc

zn

a

Rysunek 2: Sieczna i styczna do wykresu funkcji - uzasadnienie wzoru na współczynnik kierunkowy siecznej.

Styczna jest granicznym położeniem siecznych wykresu funkcji przechodzących przez punkty i , gdy , czyli współczynnik kierunkowy stycznej będzie odpowiadał granicy właściwej funkcji przy (o ile istnieje). Stąd widać już związek stycznej z pochodną funkcji.

UWAGA

Uwaga 13:

Geometrycznie styczna jest prostą, która w sąsiedztwie punktu styczności najlepiej przybliża wykres funkcji różniczkowalnej.

UWAGA

Uwaga 14:

Jeżeli jest przepisem stycznej do wykresu funkcji w punkcie , to liczba (współczynnik kierunkowy stycznej) jest równa pochodnej funkcji w punkcie .

( , f( ))

x

0

x

0

(x, f(x))

.

f(x)−f( )x0 x−x0

f

( , f( ))

x

0

x

0

(x, f(x))

x → x

0 f(x)−f( )_x−xx₀0

x → x

0

y = ax + b

f

x

0

a

f

x

0

(19)

PRZYKŁAD

Przykład 15:

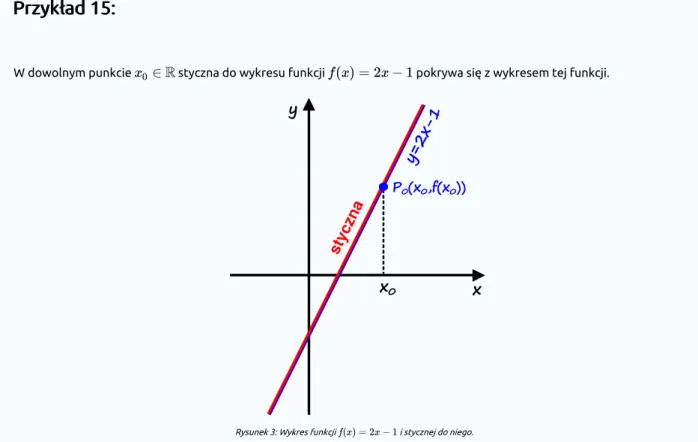
W dowolnym punkcie styczna do wykresu funkcji pokrywa się z wykresem tej funkcji.

st

yc

zn

a

Rysunek 3: Wykres funkcji i stycznej do niego.

W związku z tym, pochodna funkcji w każdym punkcie jest równa , bo jest równa współczynnikom kierunkowym stycznych do wykresu funkcji w punktach , które stale wynoszą . Zatem dla każdego .

Zwróćmy jeszcze raz uwagę, że określenie stycznej do wykresu funkcji jako prostej, która ma dokładnie jeden punkt wspólny z wykresem funkcji, jest błędne. Przykład stycznej do wykresu funkcji w punkcie , która ma więcej niż jeden punkt wspólny z wykresem przedstawia poniższy rysunek.

Rysunek 4: Wykres funkcji i stycznej do niego, które mają dwa punkty wspólne.

Natomiast w rozważaliśmy funkcję, której wykres pokrywa się ze styczną w dowolnym punkcie , czyli wykres i styczna mają nieskończenie wiele punktów wspólnych. Z drugiej strony, oczywiście, każdy z łatwością wskaże proste mające tylko jeden punkt wspólny z wykresem funkcji, a nie są stycznymi do tego wykresu.

∈ R

x

0

f(x) = 2x − 1

f(x) = 2x − 1

f

x

0

2 f

x

0

2 f

′

( ) = 2

x

0

x

0

∈ R

x

0

R

(20)

UWAGA

Uwaga 15:

Nie w każdym punkcie ciągłości funkcji istnieje styczna do wykresu tej funkcji.

UWAGA

Uwaga 16:

Jeżeli nie istnieje styczna do wykresu funkcji w punkcie , to nie istnieje również pochodna tej funkcji w punkcie .

PRZYKŁAD

Przykład 16:

Funkcja nie posiada ani stycznej, ani w .

Rysunek 5: Wykres funkcji nie mającej stycznej w punkcie .

Styczna w punkcie istnieje, jeżeli otrzymamy tą samą prostą jako graniczne położenie siecznych wykresu funkcji przy zmierzającym do z lewej strony i przy zmierzającym do z prawej strony. W przypadku funkcji każda

sieczna wykresu przechodząca przez punkty i , gdy , ma przepis , a zatem i prosta

będąca ich granicznym położeniem, przy , ma przepis . Natomiast, gdy , sieczne i prosta będąca ich granicznym położeniem mają przepis . Zatem prosta będąca położeniem granicznym lewostronnym (granica lewostronna) jest różna od prostej będącą położeniem granicznym prawostronnym (granicy prawostronnej), czyli prosta będąca położeniem granicznym obustronnym (granica obustronna) nie istnieje.

UWAGA

Uwaga 17:

Podsumowując, pochodna (właściwa) funkcji ciągłej w punkcie (czyli współczynnik kierunkowy stycznej w tym punkcie) będzie istniała, jeżeli będzie istniała styczna do wykresu funkcji w tym punkcie oraz będzie miała równanie kierunkowe (czyli styczna nie będzie pionowa).

W ostatniej uwadze został wspomniany przypadek pionowej stycznej do wykresu funkcji. Taka sytuacja ma miejsce, gdy funkcja

x

0

x

0

k(x) = |x − 3|

x

0

= 3

k(x) = |x − 3| x0= 3

x

0

x

0

x

0

k(x) = |x − 3|

( , k( ))

x

0

x

0

(x, k(x))

x < x

0

y = −x + 3

x → x

0

y = −x + 3

x > x

0

y = x − 3

x

0

O( )

0

(21)

jest ciągła w otoczeniu i obie pochodne jednostronne w są niewłaściwe (pochodna obustronna może istnieć lub nie).

st

yc

zn

a

Rysunek 6: Pionowa styczna do wykresu funkcji - istnieje pochodna niewłaściwa w .

st

yc

zn

a

Rysunek 7: Pionowa styczna do wykresu funkcji - nie istnieje pochodna w .

Zwróćmy uwagę, że przypadek stycznej pionowej spełnia definicję stycznej do wykresu funkcji. Przykładem takiej stycznej jest prosta , która jest styczną do wykresu funkcji w punkcie .

Dla ustalonego można łatwo wyprowadzić przepis na styczną do wykresu funkcji, jeżeli funkcja ma pochodną (właściwą) w punkcie . Na podstawie wcześniejszych obserwacji równanie stycznej do wykresu funkcji w punkcie ma postać Ponadto punkt styczności należy do stycznej, więc

Zatem równanie stycznej do wykresu funkcji w punkcie ma postać: Na podstawie tego wyprowadzenia sformułujmy twierdzenie.

TWIERDZENIE

Twierdzenie 8: o równaniu stycznej do wykresu funkcji

Niech oraz funkcja będzie określona w otoczeniu i posiada pochodną (właściwą) w punkcie . Równanie stycznej do wykresu funkcji w punkcie ma postać

O( )

x

0

x

0 x0 x0

x = 0

f(x) = x

√

3

_x

_{= 0}

0

∈ R

x

0

x

0

f

x

0

y = ( ) ⋅ x + b.

f

′

_x

₀

( , f( ))

x

0

x

0

f( ) = ( ) ⋅

x

0

f

′

x

0

x

0

+ b, st

ą

d b = f( ) − ( ) ⋅ .

x

0

f

′

x

0

x

0

f

x

0

y = ( ) ⋅ x + f( ) − ( ) ⋅ .

f

′

_x

₀

_x

₀

_f

′

_x

₀

_x

₀

∈ R

x

0

f

O( )

x

0

x

0

f

x

0

y = ( )(x − ) + f( ).

f

′

_x

₀

_x

₀

_x

₀

(22)

PRZYKŁAD

Przykład 17:

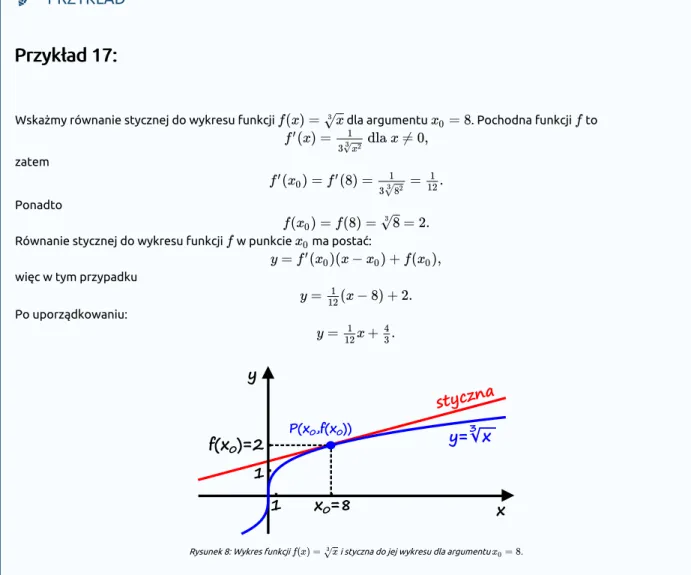
Wskażmy równanie stycznej do wykresu funkcji dla argumentu . Pochodna funkcji to zatem

Ponadto

Równanie stycznej do wykresu funkcji w punkcie ma postać: więc w tym przypadku

Po uporządkowaniu:

Rysunek 8: Wykres funkcji i styczna do jej wykresu dla argumentu .

Znając własności współczynnika kierunkowego prostej , możemy sformułować następujące twierdzenie.

TWIERDZENIE

Twierdzenie 9: o kącie nachylenia stycznej do dodatniej części osi

Niech oraz funkcja będzie określona w otoczeniu i posiada pochodną (właściwą) w punkcie . Niech oznacza miarę kąta skierowanego między dodatnią częścią osi i styczną do wykresu funkcji w punkcie . Wtedy

Jednym z zastosowań stycznej, a tym samym pochodnej funkcji, jest określenie kąta między krzywymi będącymi wykresami funkcji, które się przecinają.

f(x) = x

√

3

_x

_{= 8}

0

f

(x) =

dla x ≠ 0,

f

′ 1 3 x_√3 2

( ) = (8) =

= .

f

′

_x

₀

_f

′ 1 3 8_√3 2 ₁₂1

f( ) = f(8) =

x

0

√

3

8 = 2.

f

x

0

y = ( )(x − ) + f( ),

f

′

_x

₀

_x

₀

_x

₀

y = (x − 8) + 2.

1 12

y = x + .

1 12 43 f(x) = x√3 _x _{= 8} 0

a

y = ax + b

Ox

∈ R

x

0

f

O( )

x

0

x

0

α

Ox

f

( , f( ))

x

0

x

0

tg α = ( ).

f

′

_x

₀

(23)

DEFINICJA

Definicja 13: Kąt przecięcia się wykresów funkcji

Niech . Niech funkcje i będą określone w otoczeniu , posiadają pochodne właściwe lub niewłaściwe w punkcie oraz ich wykresy mają punkt wspólny .

Kątem przecięcia się wykresów funkcji

Kątem przecięcia się wykresów funkcji i i w punkcie w punkcie nazywamy kąt ostry lub prosty między stycznymi do wykresów tych funkcji w punkcie przecięcia .

y=g(x)

y=f(x)

styczna

styc

_zna

Rysunek 9: Kąt przecięcia się wykresów funkcji i .

Kąt przecięcia się wykresów funkcji możemy obliczyć, wykorzystując twierdzenie:

TWIERDZENIE

Twierdzenie 10: o kącie przecięcia się wykresów funkcji

Niech . Niech funkcje i będą określone w otoczeniu , posiadają pochodne (właściwe) w punkcie oraz ich wykresy mają punkt wspólny . Miara kąta przecięcia się wykresów funkcji i w punkcie wyraża się wzorem

Jeżeli , to .

Powyższy wzór jest konsekwencją wzoru na tangens różnicy kątów oraz związku pochodnej funkcji w punkcie ze styczną do wykresu funkcji w tym punkcie. Wartość jest równa tangensowi kąta lub kąta do niego przyległego. Wartość tangensa dla kątów przyległych różni się tylko znakiem. Szukamy tangensa dodatniego kąta ostrego, więc właściwą wartość wybieramy przez zastosowanie wartości bezwzględnej.

Różniczka funkcji i jej zastosowanie do obliczeń

przybliżonych

Z pojęciem pochodnej wiąże się pojęcie różniczki. Funkcja posiadająca pochodną (właściwą) w danym zbiorze jest nazywana funkcją różniczkowalną w tym zbiorze, ale czym jest różniczka?

∈ R

x

0

f g

O( )

x

0

x

0

( , )

x

0

y

0

f g

( , )

x

0

y

0

( , )

x

0

y

0 f g

∈ R

x

0

f g

O( )

x

0

x

0

( , )

x

0

y

0

φ

f g

( , )

x

0

y

0

φ = arctg

∣

_∣

f′( )− ( )x0 g′x0

, gdy ( ) ( ) ≠ −1.

1+ ( ) ( )f′_x 0g′x0

∣

f

′

x

0

g

′

x

0

( ) ( ) = −1

f

′

_x

₀

_g

′

_x

₀

_{φ =}

π 2 ( )− ( ) f′_x 0 g′x0 1+ ( ) ( )f′_x 0g′x0

φ

(24)

DEFINICJA

Definicja 14: Różniczka funkcji

Niech i funkcja ma pochodną właściwą w punkcie . Różniczką funkcji

Różniczką funkcji w punkcje w punkcje nazywamy funkcję zmiennej określoną wzorem

UWAGA

Uwaga 18:

Zauważmy, że różniczka funkcji w danym punkcje jest funkcją liniową postaci , gdzie jest stałą, a jest zmienną.

UWAGA

Uwaga 19:

Jeżeli funkcja ma pochodną właściwą w punkcie , to lub w innej postaci

Zatem i stąd czyli

Przy czym błąd przybliżenia , jaki popełniamy, spełnia warunek

czyli dąży do zera szybciej niż . Przyjrzyjmy się wzorowi

Oznaczmy argument przez . Wtedy i

Prawa strona tego wzoru to przepis stycznej do wykresu funkcji w punkcie , zatem interpretacją geometryczną przybliżenia funkcji przez powyższy wzór jest przybliżenie wykresu funkcji przez styczną do wykresu tej funkcji w punkcie .

Analizując powyższy wzór możemy również zauważyć, że pochodna funkcji w punkcie jest przybliżonym współczynnikiem proporcjonalności zmiany wartości funkcji do zmiany argumentu:

Liczba jest zmianą zmiennej niezależnej (argumentu) funkcji , zaś jest zmianą wartości funkcji odpowiadającym zmianie argumentu .

∈ R

x

0

f

x

0

f

x

0

df

x0

h

d (h) = ( ) ⋅ h.

f

x0

f

′

x

0

f

x

0

y = ah

a = ( )

f

′

x

0

h

f

x

0

∈ R

( ) =

,

f

′

_x

₀

_lim

h→0 f( +h)−f( )x0 x0 h

= 0.

lim

h→0 f( +h)−f( )− ( )⋅hx0 x0 f′x0 h

( ) ≈

f

′

_x

₀ f( +h)−f( )x0 x0 h

f( + h) ≈ f( ) + ( ) ⋅ h,

x

0

x

0

f

′

x

0

f( + h) ≈ f( ) + d (h).

x

0

x

0

f

x0

f( + h) − f( ) − d (h)

x

0

x

0

f

x0

= 0,

lim

h→0 f( +h)−f( )−d (h)x0 x0 f_x0 h

h

f( + h) ≈ f( ) + ( ) ⋅ h.

x

0

x

0

f

′

x

0

+ h

x

0

x

h = x − x

0

f(x) ≈ f( ) + ( ) ⋅ (x − ).

x

0

f

′

x

0

x

0

f

x

0

x

0

f

x

0

f

f(x) − f( ) ≈ ( )(x − ).

x

0

f

′

x

0

x

0

x − x

0

f

f(x) − f( )

x

0

x − x

0

(25)

PRZYKŁAD

Przykład 18:

Wyznaczymy różniczki funkcji w punktach i . Aby to zrobić obliczmy najpierw i :

Zatem skoro , to

PRZYKŁAD

Przykład 19:

Za pomocą różniczki określmy przybliżoną wartość liczby .

Przybliżymy wartość za pomocą różniczki funkcji w punkcie , według wzoru

. Dlaczego w punkcie ? Punkt jest niewygodny dla obliczenia , wiec zastąpimy go leżącym blisko niego na osi rzeczywistej punktem bardziej wygodnym dla obliczenia , bo .

f(x) = 3

x2

= 1

x

1

x

2

= 4

f

′

(1)

f

′

(4)

(x)

f

′

(1)

f

′

(4)

f

′

=

3

x2

ln 3 ⋅ 2x

= ln 3 ⋅ 2 = 6 ln 3

3

1

=

3

16

ln 3 ⋅ 8 = 344373768 ln 3

d (h) = ( ) ⋅ h

f

x0

f

′

x

0

d (h)

f

1

d (h)

f

4

= d

f

x1=1

(h) = 6 ln 3 ⋅ h

= d

f

x2=4

(h) = 344373768 ln 3 ⋅ h

8, 2

−−

−

√

3

8, 2

−−

−

√

3

_{f(x) = x}

_√

3

_{x = 8}

f(x) ≈ f( ) + d (x − )

x

0

f

x0

x

0

x = 8

x = 8, 2

√

3

x

= 8

x

0

√

3

x

−−

0

√

3

8 = 2

x = 8, 2 - punkt niewygodny

= 8

- punkt wygodny bliski x

x

0

f( ) =

x

0

√

3

8 = 2

(x) =

f

′

1 3 x

_√

3

−−

2

(8) =

=

f

′

1 3 8

_√

3

−−

2

1

12 x −

x

0

= 0, 2

f(x) ≈ f( ) + ( ) ⋅ (x − )

x

0

f

′

x

0

x

0

≈ 2 +

⋅ 0, 2 =

8, 2

−−

−

√

3

1

12

121

60

(26)

PRZYKŁAD

Przykład 20:

Za pomocą różniczki obliczmy w przybliżeniu wartość liczby .

Pochodne wyższych rzędów. Wzór Taylora

Możemy obliczyć pochodną funkcji pochodnej. W ten sposób otrzymujemy pochodną rzędu drugiego zadanej funkcji, a także pochodne wyższych rzędów. Pojęcie pochodnych wyższych rzędów znajduje zastosowanie między innymi we wzorze Taylora, który umożliwia przybliżanie funkcji w lepszy sposób niż robi to różniczka funkcji czy geometrycznie styczna.

DEFINICJA

Definicja 15: Pochodna rzędu

Definicja 15: Pochodna rzędu funkcji w punkcie

funkcji w punkcie

Niech .

Pochodną (właściwą) rzędu

Pochodną (właściwą) rzędu funkcji funkcji w punkcie w punkcie (lub pochodną pochodną -tego rzędu funkcji -tego rzędu funkcji w punkcie w punkcie ) oznaczamy przez i definiujemy jako

o ile funkcja jest określona w otoczeniu punktu i istnieje pochodna funkcji w punkcie . Przyjmujemy, że .

DEFINICJA

Definicja 16: Funkcja pochodna rzędu

Funkcję określoną w przedziale , której wartości w punktach są równe , nazywamy funkcją pochodną rzędu funkcją pochodną rzędu funkcji

funkcji w przedziale w przedziale lub pochodną pochodną -tego rzędu funkcji -tego rzędu funkcji w przedziale w przedziale , lub też -tą pochodną funkcji -tą pochodną funkcji w przedziale w przedziale i

oznaczamy dla .

7, 7

−−

−

√

3

x = 7, 7 - punkt niewygodny

= 8

- punkt wygodny bliski x

x

0

f( ) =

x

0

√

3

8 = 2

(x) =

f

′

1 3 x

_√

3

−−

2

(8) =

=

f

′

1 3 8

_√

3

−−

2

1

12 x −

x

0

= −0, 3

f(x) ≈ f( ) + ( ) ⋅ (x − )

x

0

f

′

x

0

x

0

≈ 2 +

⋅ (−0, 3) =

7, 7

−−

−

√

3

1

12

79

40 n

n ∈ N

n

f

x

0

n

f

x

0

( )

f

(n)

_x

₀

( ) =

( ) dla n ≥ 2,

f

(n)

_x

₀

_[

_f

(n−1) ′

_]

_x

₀

f

(n−1)

_x

₀

_f

(n−1)

_x

₀

( ) = ( )

f

(1)

_x

₀

_f

′

_x

₀

n

I

x ∈ I

f

(n)

(x)

_n

f

I

n

f

I

n

f

I

f

(n)

_{n ∈ N}

(27)

UWAGA

Uwaga 20:

Pochodne wyższych rzędów oznaczamy również w następujący sposób:

Ponadto przyjmuje się oznaczenie:

UWAGA

Uwaga 21:

Dla istnienia pochodnej rzędu funkcji w punkcie konieczne jest istnienie w pewnym otoczeniu punktu . Natomiast dla istnienia pochodnej rzędu funkcji w przedziale otwartym konieczne jest istnienie w tym samym przedziale otwartym , ponieważ dla każdego punktu z przedziału otwartego istnieje otoczenie tego punktu, które zawiera się w tym przedziale. Są to warunki konieczne istnienia pochodnej rzędu , ale nie są to warunki wystarczające, czyli jest możliwa sytuacja, gdy istnieje pochodna rzędu danej funkcji, ale pochodna rzędu już nie.

UWAGA

Uwaga 22:

jest nazywana definicją indukcyjną, ponieważ pochodną rzędu definiujemy za pomocą pochodnej rzędu , czyli definiujemy pojęcie dla za pomocą tego samego pojęcia określonego dla liczb naturalnych mniejszych od . Indukcyjnie również definiujemy pochodne jednostronne wyższego rzędu:

DEFINICJA

Definicja 17: Pochodna lewostronna rzędu

Definicja 17: Pochodna lewostronna rzędu funkcji w punkcie

funkcji w punkcie

Niech .

Pochodną lewostronną (właściwą) rzędu

Pochodną lewostronną (właściwą) rzędu funkcji funkcji w punkcie w punkcie oznaczamy przez i definiujemy jako

o ile funkcja jest określona w otoczeniu lewostronnym punktu i istnieje pochodna lewostronna funkcji w