Wykład I
Literatura
Podręczniki
1. G. M. Fitherholz – „Rachunek różniczkowy i całkowy” 2. W. Żakowski – „Matematyka” tom I
Zbiory zadań
1. W. Krysicki, L. Włodarski – „Analiza matematyczna w zadaniach” tom I i II 2. J. Banaś, Wędrychowicz – „Zbiór zadań z analizy matematycznej”
Oznaczenia
∀ – kwantyfikator ogólny (dla każdego)
∃ – kwantyfikator szczegółowy (istnieje)
ℕ – zbiór liczb naturalnych
ℤ – zbiór liczb całkowitych
ℚ – zbiór liczb wymiernych
ℝ – zbiór liczb rzeczywistych
ℂ – zbiór liczb zespolonych
𝑜𝑡(𝑥
0) – zbiór wszystkich otoczeń punktu 𝑥
0𝐶
[𝑎,𝑏] – zbiór funkcji ciągłych na przedziale(𝑎, 𝑏) i prawostronnie ciągłych w 𝑎 oraz lewostronnie ciągłych w 𝑏𝐶(𝐴) – zbiór funkcji ciągłych na 𝐴
𝐷(𝐴) – zbiór funkcji różniczkowych na 𝐴
𝐶
𝑛(𝐴)
– zbiór funkcji n-krotnie różniczkowalnych w sposób ciągły na 𝐴𝐷
𝑛(𝐴)– zbiór funkcji n-krotnie różniczkowalnych na 𝐴
Logika
Definicja 1.1 (Zdanie logiczne)
Zdaniem logicznym nazywamy wyrażenie, któremu można przypisać ocenę prawdy lub fałszu.
Oznaczenia logiczne
𝑝, 𝑞 – zdania logiczne 𝑝 ∨ 𝑞 – alternatywa 𝑝 ∧ 𝑞 – koniunkcja 𝑝 ⟹ 𝑞 – implikacja 𝑝 ⟺ 𝑞 – równoważność ~𝑝 – negacjaTautologia
Definicja 1.2 (Tautologia)Prawem logicznym nazywamy zdanie które jest zawsze prawdziwe. Udowadniamy za pomocą tabelki logicznej.
Prawo podwójnego zaprzeczenia: 𝑝 ⟺ ~(~𝑝) Prawo wyłączonego środka: 𝑝 ∨ ~𝑞
Prawo sprzeczności: ~(𝑝 ∧ ~𝑝)
Prawa De Morgana
I prawo: ~(𝑝 ∧ 𝑞) ⟺ ~𝑝 ∨ ~𝑞 II prawo: ~(𝑝 ∨ 𝑞) ⟺ ~𝑝 ∧ ~𝑞
Dowód I prawa De Morgana:
𝑝 𝑞 𝑝 ∧ 𝑞 ~𝑝 ~𝑞 ~(𝑝 ∧ 𝑞) ~𝑝 ∨ ~𝑞 ~(p ^ q ) ~p v ~q
1 1 1 0 0 0 0 1
0 1 0 1 0 1 1 1
1 0 0 0 1 1 0 1
Twierdzenia
Twierdzenie: 𝒁ałożenie ⟹ 𝑻eza Twierdzenie odwrotne: 𝑇 ⟹ 𝑍 Kontrapozycja: ~𝑇 ⟹ ~𝑍
Prawo transpozycji: (𝑍 ⟹ 𝑇) ⟺ (~𝑇 ⟹ ~𝑍)
Dowód prawa transpozycji:
𝑇 𝑍 ~𝑇 ~𝑍 𝑍 ⟹ 𝑇 ~𝑇 ⟹ ~𝑍 (𝑍 ⟹ 𝑇) ⟺ (~𝑇 ⟹ ~𝑍)
0 1 1 0 0 0 1
1 1 0 0 1 1 1
1 0 0 1 1 1 1
0 0 1 1 1 1 1
Wyrażenia zawierające zmienne, nazywamy formą zdaniową, np.: 𝑥2+ 𝑦2 > 0
Zbiory
Definicja 1.3 (Zbiory) 𝐴, 𝐵 – zbiory 𝐴 = 𝐵 ∶⟺ ∀𝑥 𝑥 ∈ 𝐴 ⟺ 𝑥 ∈ 𝐵 𝐴 ⊂ 𝐵 ∶⟺ ∀𝑥 𝑥 ∈ 𝐴 ⇒ 𝑥 ∈ 𝐵Definicja 1.4 (Działania na zbiorach)
𝐴, 𝐵 – zbiory
𝐴 ∪ 𝐵 ∶= 𝑥: 𝑥 ∈ 𝐴 ∨ 𝑥 ∈ 𝐵 – połączenie (suma) 𝐴 ∩ 𝐵 ∶= 𝑥: 𝑥 ∈ 𝐴 ∧ 𝑥 ∈ 𝐵 – przecięcie (iloczyn) 𝐴\𝐵 ∶= { 𝑥: 𝑥 ∈ 𝐴 ∧ 𝑥 ∉ 𝐵} – dopełnienie B do A (różnica)
𝑋 – przestrzeń
𝑋\𝐴 – dopełnienie zbioru 𝐴 do przestrzeni 𝑋
Definicja 1.5 (Rodzina zbiorów, połączenie i przecięcie dowolnej ilości zbiorów) ℝ ⊃ 𝐼 ∋ 𝑖 → 𝐴𝑖, 𝐴𝑖 – zbiór 𝐴𝑖 𝑖∈𝐼 = 𝑥:∃𝑖∈𝐼 𝑥 ∈𝐴𝑖 – połączenie 𝐴𝑖 𝑖∈𝐼 = 𝑥: ∀𝑥∈𝐼 𝑥 ∈𝐴𝑖 – przecięcie Przykład 1.1 Wyznaczyć: 1. 𝑖∈ℝ𝐴𝑖 2. 𝑖∈ℝ𝐴𝑖 Rozwiązanie: 1. 𝑖∈ℝ𝐴𝑖 = −∞, +∞ Uzasadnienie: 𝑖𝑛𝑓𝑖∈ℝ −𝑖2− 1 = −∞ 𝑠𝑢𝑝𝑖∈ℝ 2 + 𝑖2 = +∞ 2. 𝑖∈ℝ𝐴𝑖 = (−1,2) Uzasadnienie: 𝑖𝑛𝑓𝑖∈ℝ −𝑖2− 1 = −1 𝑠𝑢𝑝𝑖∈ℝ 2 + 𝑖2 = 2 𝐴𝑖= −𝑖2− 1, 2 + 𝑖2 𝑖 ∈ℝ Wykres prawych końców przedz. 𝐴𝑖 Wykres lewych końców przedz. 𝐴𝑖
Funkcje
Dana jest funkcja: 𝑓: 𝑋 ∋ 𝑥→𝑦 = 𝑓(𝑥) ∈ 𝑌 𝑿 – zbiór argumentów
𝒀– zbiór wartości
𝒚 = 𝒇 𝒙 – równanie wykresu
Uwaga!
Aby określić funkcję, musimy zadać zbiór argumentów, zbiór wartości i wykres.
Definicja 1.6 (Dziedzina i przeciwdziedzina)
𝐷𝑓 = 𝑥 ∈ 𝑋: ∃𝑦 ∈𝑌 𝑦 = 𝑓 𝑥
𝐷𝑓−1 = {𝑦 ∈ 𝑇: ∃
𝑥∈𝑋 𝑦 = 𝑓 𝑥 }
Definicja 1.7 (Odwzorowanie)
Funkcja f : X -> Y nazywa się odwzorowaniem jeżeli 𝐷𝑓 = 𝑋
Definicja 1.8 (Iniekcja, suriekcja, bijekcja)
Iniekcja (funkcja różnowartościowa) – jest odwzorowaniem, które dla dowolnych dwóch różnych
argumentów przyjmuje różne wartości.
Tzn. 𝐷𝑓 = 𝑋 ∧ ∀𝑥1,𝑥2∈𝑋 𝑓 𝑥1 = 𝑓 𝑥2 ⇒ 𝑥1 = 𝑥2
Suriekcja – odwzorowanie, przyjmuje wszystkie wartości ze zbioru 𝑌.
Tzn. 𝐷𝑓 = 𝑋 ∧ ∀𝑦∈𝑌 ∃𝑥∈𝑋 ∶ 𝑦 = 𝑓(𝑥)
Bijekcja – funkcja będąca jednocześnie iniekcja i suriekcją. Innymi słowy taka, że każdemu
elementowi obrazu odpowiada dokładnie jeden element dziedziny.
Definicja 1.9 (Funkcja odwrotna)
Niech: 𝑓: 𝑥 ∋ 𝑋 → 𝑦 = 𝑓(𝑥) ∈ 𝑌 jest bijekcją, wówczas 𝑓−1: 𝑌 ∋ 𝑥 → 𝑦 = 𝑓−1(𝑥) ∈ 𝑋
jest odwzorowaniem odwrotnym, przy czym 𝑦 = 𝑓−1 𝑥 ⇔ 𝑓 𝑦 = 𝑥
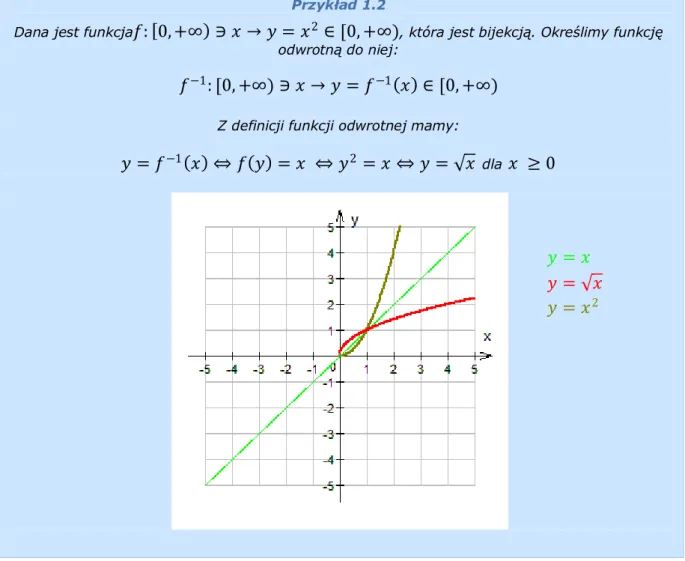
Przykład 1.2
Dana jest funkcja𝑓: 0, +∞ ∋ 𝑥 → 𝑦 = 𝑥2∈ [0, +∞), która jest bijekcją. Określimy funkcję
odwrotną do niej:
𝑓−1: [0, +∞) ∋ 𝑥 → 𝑦 = 𝑓−1 𝑥 ∈ [0, +∞)
Z definicji funkcji odwrotnej mamy:
𝑦 = 𝑓−1 𝑥 ⇔ 𝑓 𝑦 = 𝑥 ⇔ 𝑦2 = 𝑥 ⇔ 𝑦 = 𝑥 dla 𝑥 ≥ 0
Uwaga!
Wykres funkcji odwrotnej otrzymujemy przez symetrię wykresu funkcji zadanej względem prostej 𝑦 = 𝑥
𝑦 = 𝑥
𝑦 = 𝑥 𝑦 = 𝑥2
Funkcje cyklometryczne
Funkcja sinus i odwrotna do niej arcussinus
Funkcja 𝑠𝑖𝑛(𝑥) nie jest bijekcją (nie istnieje funkcja odwrotna), w związku z czym zawężamy 𝑠𝑖𝑛(𝑥) do przedziału −𝜋2,𝜋2
. Wynikiem takiego zabiegu jest funkcja:
𝑠𝑖𝑛 −𝜋 2,𝜋2 : − 𝜋 2, 𝜋 2 ∋ 𝑥 →𝑦 = 𝑠𝑖𝑛𝑥 ∈ [−1,1] Natomiast funkcja do niej odwrotna to arcussinus:
𝑎𝑟𝑐𝑠𝑖𝑛: −1,1 ∋ 𝑥→𝑦 = 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 ∈ −𝜋 2, 𝜋 2 𝑦 = 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 𝑠𝑖𝑛𝑦 = 𝑥 𝑥 ∈ [−1,1] 𝑦 ∈ [−𝜋 2, 𝜋 2]
Przykład 1.3 Rozwiąż równanie: 1. 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 =𝜋 4 2. 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 = 0 3. 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 = −34𝜋 ad. 1) Sprawdzamy założenia 𝜋
4 ∈ − 𝜋 2, 𝜋 2 , 𝑥 ∈ [−1,1] zatem 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 =𝜋 4⟺ 𝑥 = 𝑠𝑖𝑛 𝜋 4 ⟺ 𝑥 = 2 2 ∈ [−1,1] ad. 2) Sprawdzamy założenia 0 ∈ −𝜋
2, 𝜋
2 , 𝑥 ∈ [−1,1] zatem
𝑎𝑟𝑐𝑠𝑖𝑛𝑥 = 0 ⟺ 𝑥 = 𝑠𝑖𝑛 0 ⟺ 𝑥 = 0 ∈ [−1,1] ad. 3) Sprawdzamy założenia −34𝜋 ∉ −𝜋2,𝜋2 zatem równanie jest sprzeczne
𝑎𝑟𝑐𝑠𝑖𝑛𝑥 = −3
4𝜋 ⟺ 𝑥 ∈ ∅ Funkcja cosinus i odwrotna do niej arcuscosinus
Funkcja 𝑐𝑜𝑠(𝑥) nie jest bijekcją (nie istnieje funkcja odwrotna), w związku z czym zawężamy 𝑐𝑜𝑠(𝑥) do przedziału 0, 𝜋 . Wynikiem takiego zabiegu jest funkcja:
𝑐𝑜𝑠 𝑜,𝜋 : [0, 𝜋] ∋ 𝑥 →𝑦 = 𝑐𝑜𝑠𝑥 ∈ [−1,1]
Natomiast funkcja do niej odwrotna to arcuscosinus: 𝑎𝑟𝑐𝑐𝑜𝑠: −1,1 ∋ 𝑥 →𝑦 = 𝑎𝑟𝑐𝑐𝑜𝑠𝑥 ∈ 0, 𝜋
𝑦 = 𝑎𝑟𝑐𝑐𝑜𝑠𝑥
𝑐𝑜𝑠𝑦 = 𝑥 Funkcja tangens i odwrotna do niej arcustangens
Funkcja 𝑡𝑔(𝑥) nie jest bijekcją (nie istnieje funkcja odwrotna), w związku z czym zawężamy 𝑡𝑔(𝑥) do przedziału −𝜋2,𝜋2 . Wynikiem takiego zabiegu jest funkcja:
𝑡𝑔 −𝜋 2,𝜋2 : − 𝜋 2, 𝜋 2 ∋ 𝑥 →𝑦 = 𝑡𝑔𝑥𝜖ℝ Natomiast funkcja do niej odwrotna to arcustangens:
𝑎𝑟𝑐𝑡𝑔: ℝ ∋ 𝑥 →𝑦 = 𝑎𝑟𝑐𝑡𝑔𝑥 ∈ −𝜋 2, 𝜋 2 𝑦 = 𝑎𝑟𝑐𝑡𝑔𝑥 𝑡𝑔𝑦 = 𝑥 𝑥 ∈ [−1,1] 𝑦 ∈ [0, 𝜋] 𝑥 ∈ ℝ 𝑦 ∈ −𝜋 2, 𝜋 2
Funkcja cotangens i odwrotna do niej arcuscotangens
Funkcja 𝑐𝑡𝑔(𝑥) nie jest bijekcją (nie istnieje funkcja odwrotna), w związku z czym zawężamy 𝑐𝑡𝑔(𝑥) do przedziału 0, 𝜋 . Wynikiem takiego zabiegu jest funkcja:
𝑐𝑡𝑔 𝑜,𝜋 : 𝑥𝜖(0, 𝜋)→𝑦 = 𝑐𝑡𝑔𝑥𝜖ℝ
Natomiast funkcja do niej odwrotna to arcuscotangens: 𝑎𝑟𝑐𝑐𝑡𝑔: 𝑥𝜖ℝ→𝑦 = 𝑎𝑟𝑐𝑐𝑡𝑔𝑥𝜖 0, 𝜋
𝑦 = 𝑎𝑟𝑐𝑐𝑡𝑔𝑥
c𝑡𝑔𝑦 = 𝑥
𝑥 ∈ ℝ 𝑦 ∈ 0, 𝜋