Zastosowanie twierdzenia Darboux do rozwiązywania równań

Ciągłość funkcji jednej

zmiennej rzeczywistej

Autorzy:

Anna Barbaszewska-Wiśniowska

Spis treści

Spis treści

Definicja ciągłości funkcji. Przykłady Funkcja nieciągła. Typy nieciągłości funkcji Własności funkcji ciągłych

Definicja ciągłości funkcji. Przykłady

Definicja ciągłości funkcji. Przykłady

DEFINICJA

Definicja 1: Otoczenie punktu na prostej liczbowej

Definicja 1: Otoczenie punktu na prostej liczbowej

Otoczeniem

Otoczeniem punktu punktu nazywamy każdy przedział otwarty zawierający ten punkt. Otoczeniem punktu o promieniu nazywamy przedział . Otoczenia jednostronne punktu to odpowiednio:

otoczenie lewostronne punktu : otoczenie prawostronne punktu :

DEFINICJA

Definicja 2: Ciągłość funkcji w punkcie

Definicja 2: Ciągłość funkcji w punkcie

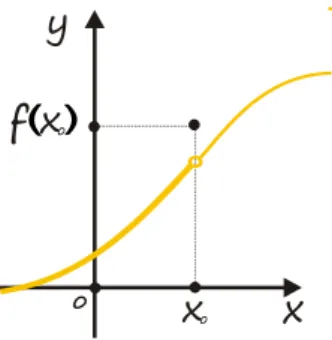
Niech funkcja będzie określona w pewnym otoczeniu . Mówimy, że funkcja funkcja jest ciągła w punkcie jest ciągła w punkcie wtedy i tylko wtedy, gdy spełnione są dwa warunki:

1. istnieje granica ,

2. granica ta jest równa wartości funkcji w punkcie , czyli .

DEFINICJA

Definicja 3: Ciągłość jednostronna

Definicja 3: Ciągłość jednostronna

Niech funkcja będzie określona przynajmniej w prawostronnym otoczeniu punktu .

Mówimy, że funkcja funkcja jest prawostronnie ciągła w punkcie jest prawostronnie ciągła w punkcie wtedy i tylko wtedy, gdy spełnione są dwa warunki: 1. istnieje granica prawostronna

2. granica ta jest równa wartości funkcji w punkcie czyli

Niech teraz funkcja będzie określona przynajmniej w lewostronnym otoczeniu punktu .

Mówimy, że funkcja funkcja jest lewostronnie ciągła w punkcie jest lewostronnie ciągła w punkcie wtedy i tylko wtedy, gdy spełnione są dwa warunki: 1. istnieje granica lewostronna

2. granica ta jest równa wartości funkcji w punkcie , czyli .

U

x

∈ R

x

r

U

= ( − r, + r)

x

x

x

x

U

= ( − r, ]

x

x

x

U

= [ , + r)

x

x

f

U

f

x

∈

D

f(x)

lim

x

lim

f(x) = f( )

x

f

x

f

x

∈

D

f(x)

lim

x

lim

f(x) = f( )

x

f

x

f

x

∈

D

f(x)

lim

x

lim

f(x) = f( )

x

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: O związku ciągłości w punkcie z ciągłością jednostronną w tym

O związku ciągłości w punkcie z ciągłością jednostronną w tym

punkcie

punkcie

Funkcja określona w otoczeniu jest ciągła w punkcie wtedy i tylko wtedy, gdy jest w tym punkcie lewostronnie i prawostronnie ciągła.

DEFINICJA

Definicja 4: Ciągłość funkcji w przedziale

Definicja 4: Ciągłość funkcji w przedziale

Funkcja

Funkcja jest ciągła w przedziale otwartym jest ciągła w przedziale otwartym , jeżeli jest ciągła w każdym punkcie tego przedziału. Funkcja

Funkcja jest ciągła w przedziale domkniętym jest ciągła w przedziale domkniętym , jeżeli jest ciągła w każdym punkcie wewnątrz tego przedziału oraz jest prawostronnie ciągła w punkcie i lewostronnie ciągła w punkcie .

Funkcja

Funkcja jest ciągła w dowolnym zbiorze jest ciągła w dowolnym zbiorze jeżeli jest odpowiednio ciągła w każdym punkcie tego zbioru. Funkcja jest ciągła

Funkcja jest ciągła, jeśli jest ciągła w całej swojej dziedzinie.

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: O ciągłości funkcji elementarnych

O ciągłości funkcji elementarnych

Wszystkie funkcje elementarne są ciągłe w swoich dziedzinach naturalnych.

U

x

f

(a, b)

f

[a, b]

a

b

PRZYKŁAD

Przykład 1: Badanie ciągłości funkcji w zadanym punkcie

Przykład 1: Badanie ciągłości funkcji w zadanym punkcie

Zbadamy ciągłość funkcji w punkcie . Dana jest funkcja

Dana jest funkcja

Rozwiązanie Rozwiązanie

Zgodnie z definicją ciągłości funkcji w punkcie musimy sprawdzić, czy istnieje granica funkcji w punkcie i czy jest ona równa wartości funkcji w tym punkcie. Aby sprawdzić istnienie granicy musimy tutaj obliczyć granice jednostronne funkcji , , gdyż funkcja w otoczeniu punktu jest dana dwoma wzorami: inaczej w lewostronnym, a inaczej w prawostronnym otoczeniu punktu .

.

Z równości granic jednostronnych wynika istnienie granicy, czyli pierwszy warunek ciągłości jest spełniony. Zauważmy, że obliczając granicę prawostronną skorzystaliśmy ze znanej granicy wyrażenia nieoznaczonego . Z istnienia tej granicy wynika istnienie i wartość odpowiedniej granicy jednostronnej.

Obliczymy wartość funkcji w punkcie .

Mamy więc , zatem funkcja jest ciągła w punkcie .

PRZYKŁAD

Przykład 2: Badanie ciągłości funkcji w zadanym punkcie

Przykład 2: Badanie ciągłości funkcji w zadanym punkcie

Zbadamy ciągłość funkcji w punkcie gdzie

Rozwiązanie Rozwiązanie

Podobnie jak w poprzednim przykładzie, badamy istnienie granicy funkcji w punkcie za pomocą granic jednostronnych.

Granice jednostronne są sobie równe, istnieje więc granica funkcji

zatem pierwszy warunek definicyjny ciągłości jest spełniony.

Wartość funkcji w punkcie nie jest równa granicy funkcji w tym punkcie, gdyż

zatem nie jest spełniony drugi warunek definicyjny ciągłości funkcji w tym punkcie. Funkcja nie jest ciągła w punkcie .

f

x

= 0

f(x) = {

= 0

+ x + 3

x

dla x > 0

dla x ≤ 0

x

x

f(x)

lim

f(x)

lim

lim

f(x)

x

x

f(x) =

( + x + 3) = 3,

lim

lim

x

f(x) =

=

⋅ 3 = 1 ⋅ 3 = 3

lim

lim

lim

= 3

lim

f

x

= 0

f(0) = + 0 + 3 = 3.

0

f(x) = f(0)

lim

f

x

= 0

f

x

= 1

f(x) =

⎧

_⎩

⎨

x

5

2 − x

dla x < 1

dla x = 1

x

= 1

dla x > 1

x

f(x) =

( ) = 1,

lim

lim

x

f(x) =

(2 − ) = 2 − 1 = 1.

lim

lim

x

f

f(x) = 1,

lim

= 1

x

f(x) = 1 ≠ f(1) = 5,

lim

f

x

= 1

PRZYKŁAD

Przykład 3: Badanie ciągłości funkcji w zadanym punkcie

Przykład 3: Badanie ciągłości funkcji w zadanym punkcie

Zbadamy ciągłość funkcji w punkcie gdzie

Rozwiązanie Rozwiązanie

Badamy istnienie granicy funkcji punkcie . W przeciwieństwie do poprzednich przykładów tu funkcja dana jest tym samym wzorem zarówno dla , jak i dla , możemy więc zapisać

Mianownik wyrażenia dąży do zera gdy . Jak zawsze w takiej sytuacji musimy zbadać, czy dąży on do zera po wartościach dodatnich czy ujemnych. Zauważamy, że dla mamy , czyli mianownik dąży do zera po wartościach ujemmnych, więc wyrażenia dąży do minus nieskończoności. Gdy wówczas i rozumując analogicznie stwierdzamy, że dązy do plus nieskonczoności. Aby kontynuować obliczanie granicy funkcji musimy przejść na granice jednostronne.

Granice jednostronne funkcji są różne, więc nie istnieje granica funkcji punkcie .

Nie jest spełniony pierwszy warunek definicyjny ciągłości, więc funkcja nie jest ciągła punkcie .

Funkcja nieciągła. Typy nieciągłości funkcji

Funkcja nieciągła. Typy nieciągłości funkcji

DEFINICJA

Definicja 5: Funkcja nieciągła

Definicja 5: Funkcja nieciągła

Funkcję

Funkcję nazywamy funkcją nieciągłą nazywamy funkcją nieciągłą, gdy nie jest ona ciągła w co najmniej jednym punkcie swojej dziedziny. Każdy taki punkt nazywamy punktem nieciągłości funkcjipunktem nieciągłości funkcji.

UWAGA

Uwaga 1:

Uwaga 1:

Funkcja nieciągła w punkcie może, ale nie musi, być ciągła jednostronnie w tym punkcie.

f

x

= 1

f(x) = {

arctg

= 1

0

dla x ≠ 1

dla x = 1

x

f

x

= 1

x < 1

x > 1

f(x) =

arctg

lim

lim

x → 1

x > 1

x − 1 < 0

x > 1

x − 1 > 0

arctg

= − ,

arctg

=

lim

lim

f

x

= 1

f

x

= 1

f

f

x

PRZYKŁAD

Przykład 4:

Przykład 4:

Dobierzemy wartość parametru tak, by funkcja dana wzorem

była nieciągła. Rozwiązanie Rozwiązanie

Dziedziną funkcji jest cały zbiór liczb rzeczywistych. Żeby funkcja była nieciągła wystarczy, by była nieciągła w przynajmniej jednym punkcie. Weźmy pod uwagę punkt . Nie istnieje granica funkcji w tym punkcie, gdyż granice jednostronne są różne.

. .

Nie jest spełniony pierwszy warunek definicyjny ciągłości, więc niezależnie od doboru stałej (wartości funkcji w zerze), funkcja nie jest ciągła w , zatem nie jest funkcją ciągłą.

(Zauważmy, że obliczając granice jednostronne skorzystaliśmy z istnienia dwóch granic podstawowych (wyrażeń nieoznaczonych) oraz . Z istnienia tych granic wynika istnienie odpowiednich granic jednostronnych.)

Odpowiedź Odpowiedź

Jako możemy przyjąć dowolna liczbę rzeczywistą.

PRZYKŁAD

Przykład 5:

Przykład 5:

Dobierzemy wartość parametru tak, by funkcja dana wzorem

była nieciągła w i jednocześnie lewostronnie ciągła w , Rozwiązanie

Rozwiązanie

Aby funkcja była lewostronnie ciągła w wartość funkcji w zerze musi być równa lewostronnej granicy tej funkcji w zerze. Mamy:

czyli musimy przyjąć , skąd . Odpowiedź

Odpowiedź

Dla funkcja nieciągła jest lewostronnie ciągła w zerze.

A

f(x) =

⎧

⎩

⎨

⎪

⎪

⎪

⎪

A

dla x < 0

dla x = 0

dla x > 0

f

= 0

x

f(x) =

=

⋅

=

lim

lim

lim

f(x) =

= 1

lim

lim

A

f

x

= 0

f

= 1

lim

lim

= 1

A

A

f(x) =

⎧

⎩

⎨

⎪

⎪

⎪

⎪

A

dla x < 0

dla x = 0

dla x > 0

= 0

x

x

= 0

x

f(0) = A,

lim

f(x) =

f(0) =

A =

A =

f

PRZYKŁAD

Przykład 6:

Przykład 6:

Dobierzemy wartość parametru tak, by funkcja dana wzorem

była nieciągła w i jednocześnie prawostronnie ciągła w . Rozwiązanie

Rozwiązanie

Podobnie jak w poprzednim przypadku, aby funkcja była prawostronnie ciągła w , musi zachodzić równość ,

czyli . Odpowiedź Odpowiedź

Dla funkcja nieciągła w zerze jest w tym punkcie funkcją prawostronnie ciągłą.

UWAGA

Uwaga 2: O nieciągłości typu ,,skokowego”

Uwaga 2: O nieciągłości typu ,,skokowego”

Gdy (jak w powyższym przykładzie) w punkcie nieciągłości istnieją skończone granice jednostronne ale są różne, to mówimy, że funkcja ma w nieciągłość typu „skok”nieciągłość typu „skok”.

(

(

Rysunek 1: C1. Nieciągłość typu „skok”.

A

f(x) =

⎧

⎩

⎨

⎪

⎪

⎪

⎪

A

dla x < 0

dla x = 0

dla x > 0

= 0

x

x

= 0

x

f(0) =

lim

f(x)

A = 1

A = 1

f

x

= 0

x

(

(

(

(

Rysunek 2: Ilustracja do uwag o nieciągłości typu "skokowego" – funkcje odpowiednio lewostronnie i prawostronnie ciągłe w punkcie nieciągłości typu „skok”.

ZADANIE

Zadanie 1:

Zadanie 1:

Treść zadania: Treść zadania:

Dobierzemy (jeżeli to możliwe) wartość parametru tak, by funkcja dana wzorem

była ciągła w .

Rozwiązanie: Rozwiązanie:

Aby funkcja była ciągła w , musi ona mieć granicę w tym punkcie i granica ta musi być równa wartości funkcji w tym punkcie. Stąd

, .

Odpowiedź Odpowiedź

Kładąc , otrzymujemy funkcję ciągłą w .

A

f(x) = {

A

dla x ≠ −1

dla x = −1

= −1

x

= −1

x

f(x) =

=

=

(x − 1) = −2

lim

lim

lim

lim

f(−1) = A

A = −2

x

= −1

ZADANIE

Zadanie 2:

Zadanie 2:

Treść zadania: Treść zadania:

Dobierzemy (jeżeli to możliwe) wartość parametru tak, by funkcja dana wzorem

była nieciągła w .

Rozwiązanie: Rozwiązanie:

Jako, że istnieje granica funkcji i - jak pokazaliśmy w ZADANIU 1 wynosi ona , więc aby funkcja nie była ciągła w tym punkcie, wystarczy dobrać jej wartość .

Odpowiedź Odpowiedź

Dla funkcja nie jest ciągła w .

ZADANIE

Zadanie 3:

Zadanie 3:

Treść zadania: Treść zadania:

Dobierzemy (jeżeli to możliwe) wartość parametru tak, by funkcja dana wzorem

była nieciągła w i jednocześnie lewostronnie ciągła w tym punkcie.

Rozwiązanie: Rozwiązanie:

Wiemy już, że aby funkcja nie była ciągła w punkcie parametr musi być różny od .

Aby funkcja była lewostronnie ciągła w punkcie wartość funkcji w tym punkcie musiałaby równać się jej granicy lewostronnej, czyli musiałaby zachodzić równość .

Z faktu istnienia granicy funkcji w punkcie wynika tu, że

więc musielibyśmy położyć , ale wtedy funkcja byłaby ciągła w punkcie . Odpowiedź

Odpowiedź

Nie można dobrać wartości parametru tak by funkcja była lewostronnie ciągła w punkcie i jednocześnie by była nieciągła w tym punkcie.

A

f(x) = {

A

dla x ≠ −1

dla x = −1

= −1

x

f(x)

lim

−2

f(−1) ≠ −2

A ≠ −2

x

= −1

A

f(x) = {

A

dla x ≠ −1

dla x = −1

= −1

x

f

x

= −1

A

−2

= −1

x

A = −2

= −1

x

f(x) = −2

lim

A = −2

x

= −1

A

f

x

= −1

UWAGA

Uwaga 3: O nieciągłości typu ,,luka”

Uwaga 3: O nieciągłości typu ,,luka”

Gdy (jak w powyższym przykładzie) w punkcie nieciągłości istnieją skończone granice jednostronne i są sobie równe ale nie są równe wartości funkcji w tym punkcie, mówimy że jest to nieciągłość typu „luka”. Obrazowo można zauważyć, że wówczas w wykresie funkcji jest „wykuta dziura”, a wartość funkcji leży „powyżej” lub „poniżej” niej.

(

(

Rysunek 3: C3. Nieciągłość typu „luka”

Własności funkcji ciągłych

Własności funkcji ciągłych

TWIERDZENIE

Twierdzenie 3: o działaniach arytmetycznych na funkcjach ciągłych

Twierdzenie 3: o działaniach arytmetycznych na funkcjach ciągłych

Jeżeli funkcje określone w zbiorze są ciągłe w punkcie , to funkcje (gdy ), są ciągłe w punkcie .

TWIERDZENIE

Twierdzenie 4: o ciągłości funkcji złożonej

Twierdzenie 4: o ciągłości funkcji złożonej

Jeżeli funkcja jest ciągła w punkcie i funkcja jest ciągła w punkcie oraz złożenie ma sens, wówczas funkcja złożona jest ciągła w punkcie .

x

f i g

A ⊂ R

x

∈ A

f + g, f − g, f ⋅ g,

g( ) = 0

x

/

x

f

x

g

y

= f( )

x

g ∘ f

TWIERDZENIE

Twierdzenie 5: o ciągłości funkcji odwrotnej

Twierdzenie 5: o ciągłości funkcji odwrotnej

Jeżeli funkcja jest ciągła i ściśle monotoniczna w przedziale , to funkcja odwrotna jest ciągła w przedziale , w szczególności:

jeśli funkcja jest ciągła i rosnąca w przedziale , to funkcja odwrotna jest ciągła i rosnąca w przedziale ,

jeśli funkcja jest ciągła i malejąca w przedziale , to funkcja odwrotna jest ciągła i malejąca w przedziale .

PRZYKŁAD

Przykład 7:

Przykład 7:

Funkcja jest ciągła i rosnąca w przedziale . Funkcja do niej odwrotna jest ciągła i rosnąca w przedziale .

=sin x 1 -π/2 -1 π/2 -π/2 π/2 [-π/2,π/2] =arcsin x

Rysunek 4: Ilustracja faktu, że funkcja odwrotna do funkcji ciągłej i rosnącej w przedziale jest również funkcją ciągłą i rosnącą.

PRZYKŁAD

Przykład 8:

Przykład 8:

Funkcja jest ciągła i malejąca w przedziale . Funkcja do niej odwrotna jest ciągła i malejąca w przedziale . =cos x 1 π/2 [0,π] =arccos x π π 1

Rysunek 5: Ilustracja faktu, że funkcja odwrotna do funkcji ciągłej i malejącej w przedziale jest również funkcją ciągłą i malejącą.

f

J

f

_f(J)

f

[a, b]

f

[f(a), f(b)]

f

[a, b]

f

[f(b), f(a)]

f(x) = sin x

[− , ]

f

(x) = arcsinx

[f(− ), f( )] = [−1, 1]

f(x) = cos x

[0, π]

f

(x) = arccosx

[f(π), f(0)] = [−1, 1]

UWAGA

Uwaga 4:

Uwaga 4:

W twierdzeniu o ciągłości funkcji odwrotnej istotne jest założenie o przedziale. Funkcja odwrotna do funkcji ciągłej w dowolnym zbiorze nie musi być ciągła. Na przykład funkcja dana wzorem

jest ciągła w zbiorze , gdyż jest ona ciągła w każdym punkcie tego zbioru, natomiast funkcja do niej odwrotna

nie jest ciągła, gdyż nie jest ona ciągła w punkcie (nie istnieje granica funkcji w tym punkcie, bo ).

Rysunek 6: Funkcja ciągła w zbiorze , do której odwrotna nie jest ciągła.

TWIERDZENIE

Twierdzenie 6: o monotoniczności funkcji ciągłej i różnowartościowej

Twierdzenie 6: o monotoniczności funkcji ciągłej i różnowartościowej

Niech funkcja będzie ciągła w przedziale . Wówczas jest różnowartościowa wtedy i tylko wtedy, gdy jest ściśle monotoniczna w tym przedziale.

TWIERDZENIE

Twierdzenie 7:

Twierdzenie 7: Weierstrassa (o osiąganiu kresów przez funkcje ciągłą w

Weierstrassa (o osiąganiu kresów przez funkcje ciągłą w

przedziale domkniętym)

przedziale domkniętym)

Jeżeli funkcja jest ciągła w przedziale domkniętym , to jest w tym przedziale ograniczona i osiąga swoje kresy tzn. istnieją takie punkty w przedziale , że

.

f(x) = { x

_{x − 1}

dla x ∈ [0, 1)

_{dla x ∈ [2, 3]}

A = [0, 1) ∪ [2, 3]

f(x) = { x

_{x + 1}

dla x ∈ [0, 1)

_{dla x ∈ [1, 2]}

= 1

x

(x) = 1 =

(x) = 2

lim

f

/ lim

f

f

[a, b]

f

f

[a, b]

,

c

c

[a, b]

f( ) =

c

inf

f(x), f( ) =

c

sup

f(x)

f( y=M a c2 b=c1 y=-M 2 c )= sup f(x) f(c )= inf f(x)1 _xϵ[a,b] xϵ[a,b]

Rysunek 7: Ilustracja twierdzenia Weierstrassa.

UWAGA

Uwaga 5:

Uwaga 5:

W twierdzeniu Weierstrassa ważne jest, by funkcja była ciągła w przedziale domkniętym. Nie wystarcza ciągłość w przedziale otwartym, bo np. funkcja ciągła w przedziale nie osiąga ani kresu dolnego ani górnego i nie jest ograniczona (bo nie jest ograniczona z dołu).

Rysunek 8: Funkcja ciągła w przedziale otwartym nieosiągająca kresów i nieograniczona.

TWIERDZENIE

Twierdzenie 8: Własność Darboux (przyjmowanie wartości pośrednich przez

Twierdzenie 8: Własność Darboux (przyjmowanie wartości pośrednich przez

funkcję ciągłą w przedziale)

funkcję ciągłą w przedziale)

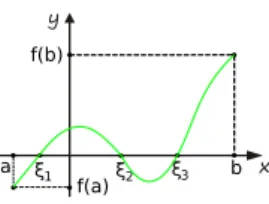
Jeżeli funkcja jest ciągła w przedziale oraz i leży pomiędzy , to istnieje taki punkt pośredni , że .

UWAGA

Uwaga 6:

Uwaga 6:

Własność Darboux orzeka, że funkcja ciągła w przedziale przyjmuje wszystkie wartości pośrednie między , więc jej wykres nie może się przerywać w tym przedziale.

f(x) =

(−1, 0)

f

[a, b]

f(a) = f(b)

/

c

f(a) i f(b)

ξ ∈ (a, b)

f(ξ) = c

a b c f(b) f(a) a b c f(a) f(b) ξ ξ ξ1 2 3

Rysunek 9: Ilustracja własności Darboux.

UWAGA

Uwaga 7: O istnieniu punktów pośrednich

Uwaga 7: O istnieniu punktów pośrednich

Z własności Darboux wynika, że przy stosownych założeniach o funkcji dla danego (z twierdzenia 6) istnieje przynajmniej jeden punkt . Może być ich więcej, gdy funkcja nie jest różnowartościowa tak jak na drugim rysunku w poprzednim przykładzie.

TWIERDZENIE

Twierdzenie 9: Wniosek z własności Darboux o znajdowaniu przybliżonych miejsc

Twierdzenie 9: Wniosek z własności Darboux o znajdowaniu przybliżonych miejsc

zerowych funkcji

zerowych funkcji

Jeżeli funkcja jest ciągła w przedziale , to istnieje punkt taki, że .

UWAGA

Uwaga 8:

Uwaga 8:

Założenie oznacza, że wartości funkcji na końcach przedziału maja różne znaki, leżą po różnych stronach osi , a jako że wykres (zgodnie z twierdzeniem Darboux) nie może się „przerywać”, więc musi przeciąć, przynajmniej raz oś . a b f(b) ξ ξ ξ1 2 3 f(a)

Rysunek 10: Ilustracja wniosku z własności Darboux o miejscach zerowych funkcji.

c

ξ

f

[a, b] oraz f(a) ⋅ f(b) < 0

ξ ∈ (a, b)

f(ξ) = 0

f(a) ⋅ f(b) < 0

0x⃗

Zastosowanie twierdzenia Darboux do

Zastosowanie twierdzenia Darboux do

rozwiązywania równań

rozwiązywania równań

PRZYKŁAD

Przykład 9: Zastosowanie wniosku z twierdzenia Darboux do rozwiązywania

Przykład 9: Zastosowanie wniosku z twierdzenia Darboux do rozwiązywania

równań

równań

Znajdziemy przybliżone pierwiastki równania . Rozwiązanie

Rozwiązanie

Najpierw sprawdzimy, czy nie znajdziemy rozwiązania pośród podzielników wyrazu wolnego. Zbiór podzielników . Oznaczając przez

mamy

Żaden z podzielników nie jest poszukiwanym rozwiązaniem. Zauważamy jednak, że wartości funkcji w obliczonych punktach maja, różne znaki. Zastosujemy wniosek z własności Darboux do przedziału . Funkcja jest ciągła na tym przedziale jako wielomian , więc na podstawie wniosku z własności Darboux w przedziale otwartym istnieje taki punkt że . Zatem równanie ma w przedziale

co najmniej jeden pierwiastek. Możemy wyznaczyć ten pierwiastek z większą dokładnością. Obliczymy wartość funkcji w punkcie , czyli w środku przedziału .

Rozważając teraz przedział zauważamy podobnie jak poprzednio, że funkcja jest ciągła na tym przedziale oraz że . Jest więc , a zatem równanie ma pierwiastek w przedziale otwartym . Postępując dalej w ten sposób, możemy wyznaczyć przybliżony pierwiastek z dowolną dokładnością.

Nie jest to jedyne rozwiązanie równania . Rozważając funkcję na przedziale mamy: . Funkcja jest ciągła na tym przedziale, więc na podstawie wniosku z własności Darboux w przedziale otwartym istnieje taki . Równanie ma więc w tym przedziale co najmniej jeden pierwiastek. Zauważmy, że pierwiastki są różne, gdyż przedziały

nie maja punktów wspólnych. Czyli równanie ma co najmniej dwa różne pierwiastki.

+ − − 2x − 2 = 0

x

_x

_x

P = {1, 2, −1, −2}

f(x) =

x

+ − − 2x − 2

_x

_x

f(1) = −3,

f(2) = 14,

f(−1) = −1,

f(−2) = 6.

[1, 2]

f

f(1) = −3 i f(2) = 14 czyli f(1) ⋅ f(2) < 0

(1, 2)

ξ

f( ) = 0

ξ

x

+ − − 2x − 2

x

x

(1, 2)

f ( ) =

> 0

[[1, ]

f

f(1) = −3 i f ( ) =

f(1) ⋅ f ( ) < 0

x

+ − − 2x − 2

x

x

(1, )

+ − − 2x − 2

x

_x

_x

_f

_{[−2, −1]}

f(−2) = 6 i f(−1) = −1 czyli f(−2) ⋅ f(−1) < 0

f

(−2, −1)

ξ

e f( ) = 0

ξ

x

+ − − 2x − 2

x

x

) i

ξ

ξ

(−2, −1) i (1, )

PRZYKŁAD

Przykład 10: Zastosowanie wniosku z własności Darboux do rozwiązywania

Przykład 10: Zastosowanie wniosku z własności Darboux do rozwiązywania

równań

równań

Pokażemy, że równanie ma dwa rozwiązania. Zauważmy, że jednym z nich jest liczba .

Pokażemy, że równanie to ma jeszcze inny pierwiastek pomiędzy zerem a jedynką.

Tworzymy funkcję , której miejsca zerowe są pierwiastkami rozwiązywanego równania. Funkcja jest ciągła w przedziale , czyli . Na podstawie wniosku z własności Darboux w przedziale otwartym , istnieje taki punkt . Zatem równanie ma w przedziale co najmniej jeden pierwiastek w sposób oczywisty różny od .

PRZYKŁAD

Przykład 11:

Przykład 11:

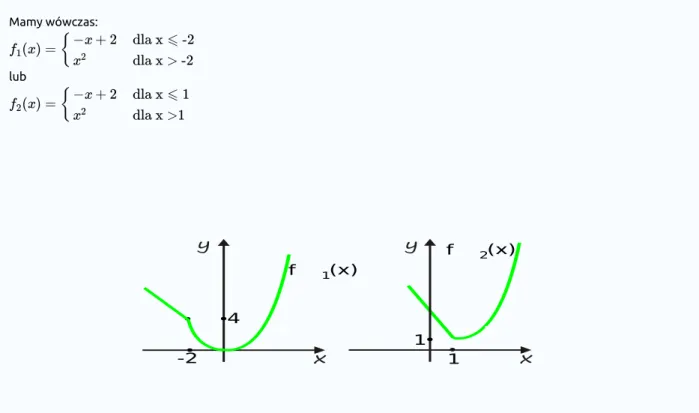
Zastanowimy się, czy można tak dobrać liczbę , aby funkcja

była ciągła.

Dziedziną funkcji jest cały zbiór liczb rzeczywistych . Aby była ciągła, musi być ona ciągła w każdym punkcie swojej dziedziny. Dla każdego punktu funkcja jest ciągła w jako funkcja elementarna (liniowa). Podobnie dla każdego punktu jest ciągła w jako funkcja elementarna (kwadratowa). Pozostaje problem ciągłości w punkcie . Możemy rozwiązać go klasycznie dobierając tak, aby istniała granica funkcji w punkcie oraz by ta granica równała się wartości funkcji .

Możemy jednak postąpić inaczej. Zauważamy, że dziedzina funkcji jest przedziałem, a z własności Darboux wiemy, że wykres funkcji ciągłej w przedziale nie może się przerwać. Narysujemy pomocniczo dwa wykresy funkcji liniowej i kwadratowej i tak dobierzemy , aby je scalić w jedną linię, którą można naszkicować bez odrywania ołówka od papieru.

-Rysunek 11: Punkty wspólne wykresów funkcji

= 4x

2

4, bo = 16 = 4 ⋅ 4

2

f(x) =

2

− 4x

_f

[0, 1] i f(0) = 1 i f(1) = −2

f(0) ⋅ f(1) < 0

(0, 1)

ξ ,

e f(ξ) = 0

2

= 4x

_{(0, 1)}

4

a

f(x) = { −x + 2

x

dla x ⩽ a

_{dla x > a}

f

R

f

x

< a

x

f

x

> a

x

f

x

x

= a

a

x

= a

lim

f(x)

f(a)

a

Na Rys. 11 widzimy, że wykresy przecinają się w dwóch punktach . Liczbę można, więc dobrać na dwa sposoby kładąc . Mamy wówczas: lub

-2

4

f

(x)

f

(x)

1

1

Rysunek 12: Wykresy dwóch różnych funkcji ciągłych powstałych wskutek sklejenia

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-09 21:09:53

Oryginalny dokument dostępny pod adresem: http://epodreczniki.open.agh.edu.pl/openagh-podreczniki_view.php? categId=4&handbookId=52

(−2, 4) oraz (1, 1)

a

a = −2 lub a = 1

(x) = {

f

−x + 2

_x

dla x ⩽ -2

_{dla x > -2}

(x) = {

f

−x + 2

_x

dla x ⩽ 1

_{dla x >1}