Analiza Matematyczna. Przegl ˛
ad własno ´sci funkcji elementarnych
Aleksander Denisiuk denisiuk@pjwstk.edu.pl
Polsko-Japo ´nska Wy˙zsza Szkoła Technik Komputerowych Wydział Informatyki w Gda ´nsku
ul. Brzegi 55 80-045 Gda ´nsk
Przegl ˛
ad własno ´sci funkcji elementarnych
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneNajnowsza wersja tego dokumentu dost ˛epna jest pod adresem
Pot ˛ega wymierna
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneTwierdzenie 1. Niech
n
∈ N
. Wtedy funkcjax
n przyx
∈ [0, +∞)
ro´snie i jest ci ˛agł ˛a.
Dowód.
x
n2− x
n1= (x
2− x
1)(x
n−12+ x
n−22x
1+ · · · + x
n−11)
.Wniosek 2. Istnieje funkcja, odwrotna do
x
n: [0, +∞) → [0, +∞)
, pierwiastek stopnian
:y
7→
√
ny
.Definicja 3. Niech
α
b ˛edzie liczb ˛a wymiern ˛a. Wtedy dlaa >
0
okre´slone jest
a
α w sposób nast ˛epuj ˛acy: 1. Dlan >
0
:x
n1=
√
na
,2. dla
m, n >
0
:a
mn= a
1Własno ´sci wymiernej pot ˛egi
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne Twierdzenie 4. 1.(a
α)
β= a
αβ,
a
α· b
α= (ab)
α,
a
α· a
β= a
α+β.
2. Dlaa >
1
orazα >
0 a
α>
1
.3. Dla
a >
1
funkcjaa
x ro´snie na zbiorze liczb wymiernych. Dowód. 2. Zało˙zymy, ˙zea
mn<
1
. 3.a
m1n1< a
m2n2 dla m1 n1<
m2 n2 .Funkcja wykładnicza
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneTwierdzenie 5. Niech dane b ˛ed ˛a
x, a
∈ R
,a >
1
. Istnieje jedyna liczba rzeczywistay
, taka, ˙ze dla dowolnych liczbα, β
∈ Q
,α < x < β
⇒ a
α6
y 6 a
β.Definicja 6. Definiujemy dla
a >
1
,x
∈ R
, pot ˛eg ˛ea
x jako jedyn ˛a liczb ˛e, okre´slon ˛a w twierdzeniu 5. Dla0 < a < 1
definiujemyWłasno ´sci funkcji wykładniczej
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne Twierdzenie 7. 1.(a
α)
β= a
αβ,
a
α· b
α= (ab)
α,
a
α· a
β= a
α+β.
2. Funkcja
a
x dlaa >
1
ro´snie, dla0 < a < 1
maleje na cał ˛a prost ˛a.3. Funkcja
a
x jest ci ˛agł ˛a∀x ∈ R
. 4. Funkcjaa
x jest dodatni ˛a∀x ∈ R
. 5. Dlaa >
1 lim
x→−∞a
x= 0
,lim
x→+∞a
x= +∞
, dla0 < a < 1
lim
x→−∞a
x= +∞
,lim
x→+∞a
x= 0
.Wykres funkcji
y
= a
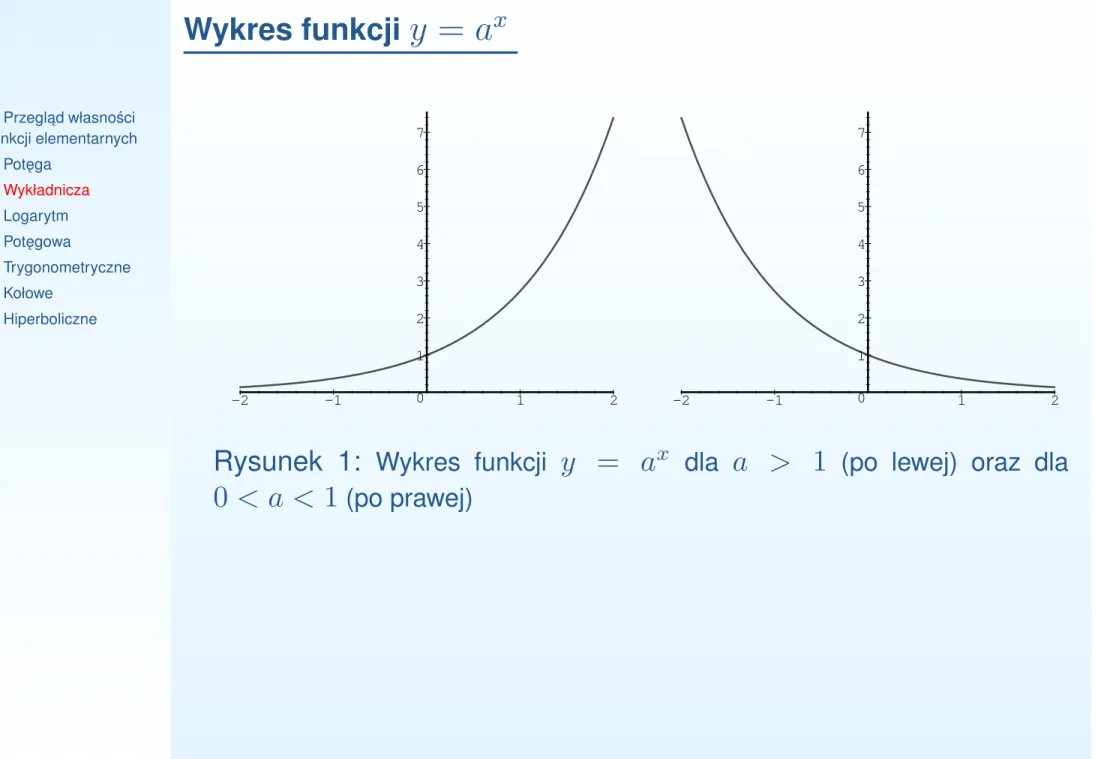
x •Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneRysunek 1: Wykres funkcji y = ax
dla a > 1 (po lewej) oraz dla
Logarytm
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneDefinicja 8. Funkcj ˛e
log
ax
: (0, +∞) → R, a ∈ (0, 1) ∪ (1, +∞)
definiujemy jako odwrotn ˛a doa
x: R → (0, +∞)
.Własno ´sci logarytmu
Twierdzenie 9. 1.
log
a(x
1· x
2) = log
ax
1+ log
ax
2,log
a(
x1x2
) = log
ax
1− log
ax
2,log
a(x
α) = α · log
ax
,log
ax
=
logb xlogba.
2. Funkcja
y
= log
ax
jest ci ˛agł ˛a i rosn ˛ac ˛a na półprostej(0, +∞)
dlaa >
1
oraz malej ˛ac ˛a dla0 < a < 1
.3.
lim
x→0+
log
ax
= −∞
, x→+∞lim
log
ax
= +∞
przya >
1
orazlim
Wykres funkcji
y
= log
ax
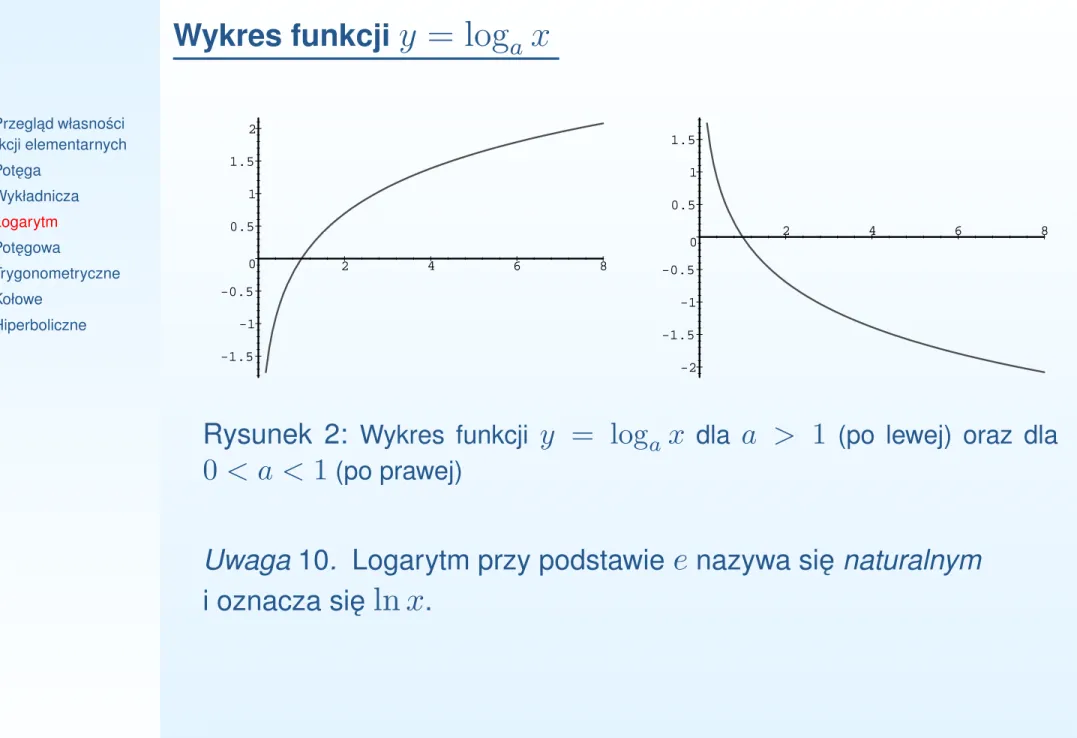
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -1.5 -1 -0.5 0 0.5 1 1.5 2 2 4 6 8 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 4 6 8Rysunek 2: Wykres funkcji y = loga x dla a > 1 (po lewej) oraz dla
0 < a < 1 (po prawej)
Uwaga 10. Logarytm przy podstawie
e
nazywa si ˛e naturalnym i oznacza si ˛eln x
.Funkcja pot ˛egowa
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneDefinicja 11. Dla
α
∈ R
, okre´slamy funkcj ˛ex
α: (0, +∞) → (0, ∞)
w sposób nast ˛epuj ˛acy:x
α= e
α ln x.Własno ´sci funkcji pot ˛egowej
Twierdzenie 12. 1. Funkcja
x
α jest funkcj ˛a ci ˛agł ˛a na(0, +∞)
. 2. Funkcjax
α jest funkcj ˛a rosn ˛ac ˛a przyα >
0
i malej ˛ac ˛a przyα <
0
na przedziale(0, +∞)
. 3.lim
x→0+
x
α
= 0
przyα >
0
orazlim
x→0+
x
α
= +∞
przyα <
0
.4.
lim
x→+∞
x
α
= +∞
przyα >
0
orazlim
x→+∞
x
Wykres funkcji
y
= x
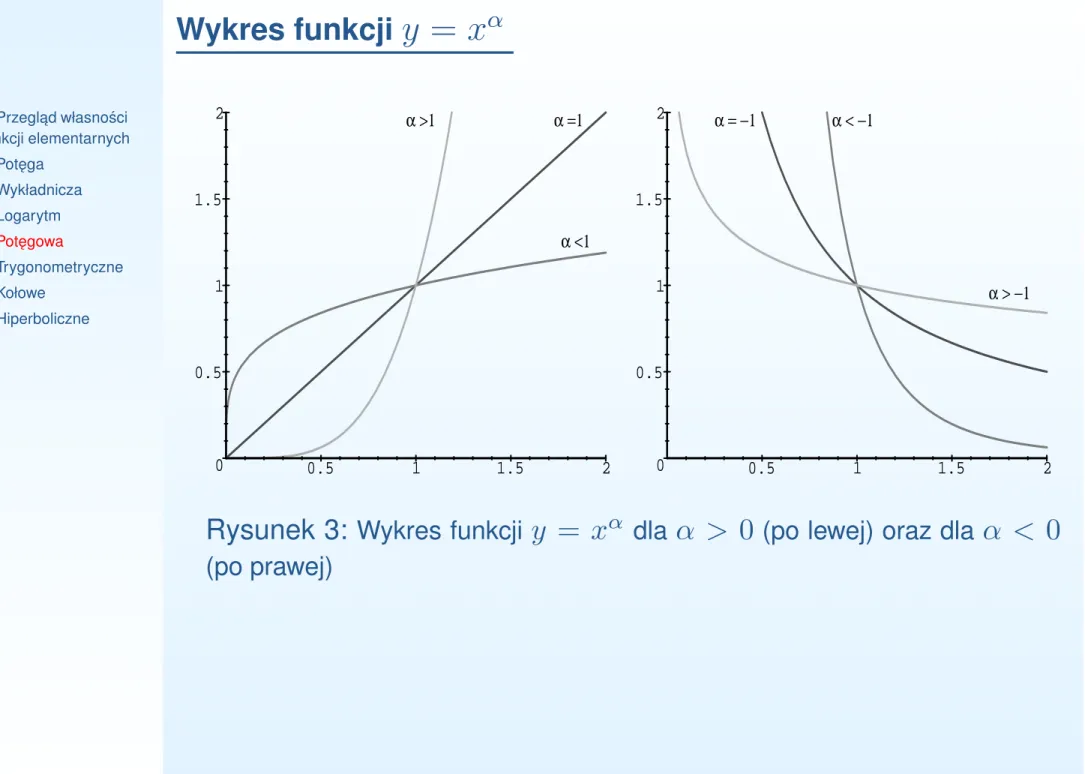
α •Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne 0 0.5 1 1.5 2 0.5 1 1.5 2 α >1 α =1 α <1 0 0.5 1 1.5 2 0.5 1 1.5 2 α < −1 α = −1 α > −1Rysunek 3: Wykres funkcji y = xα
dla α > 0 (po lewej) oraz dla α < 0 (po prawej)
Podstawowe własno ´sci funkcji trygonometrycznych
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneTwierdzenie 13. 1.
sin(x + y) = sin x cos y + cos x sin y
, 2.cos(x + y) = cos x cos y − sin x sin y
,3.
sin
2x
+ cos
2y
= 1
, 4.sin 0 = 0
,sin
π2= 1
, 5.cos 0 = 1
,cos
π2= 0
,Własno ´sci funkcji trygonometrycznych
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneWniosek 14. 1.
| sin x| 6 1
,| cos x| 6 1
, 2.sin(−x) = − sin x
,cos(−x) = cos x
, 3.sin(x − y) = sin x cos y − cos x sin y
, 4.cos(x − y) = cos x cos y + sin x sin y
, 5.sin x + sin y = 2 sin
x+y2cos
x−y2 ,6.
sin x − sin y = 2 sin
x−y2cos
x+y2 , 7.cos x = sin(
π2− x)
,8.
sin(x + 2π) = sin x
,cos(x + 2π) = cos x
, 9.| sin x| 6 |x|
.Funkcje okresowe
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneDefinicja 15. Funkcja
f
(x)
nazywa si ˛e okresow ˛a, je˙zeli istnieje minimalna liczbaT
∈ R
, takia, ˙ze∀x
zachodzif
(x + T ) = f (T )
. LiczbaT
przy tym nazywa si ˛e okresem funkcjif
(x)
.Uwaga 16. Własno´s´c 8 oznacza, ˙ze funkcje
sin x
icos x
maj ˛a okres2π
. Mo˙zna udowodni´c, ˙ze2π
jest najmniejszym z okresów. Uwaga 17. Stała funkcja nie jest okresow ˛a.Własno ´sci funkcji
sin x
oraz
cos x
. Cd.
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneTwierdzenie 18. Funkcje
sin x
orazcos x
s ˛a ci ˛agłe na całej prostejR
.Dowód.
•
sin x
jest ci ˛agł ˛a w zerze.•
sin x − sin x
n= 2 cos
x+x2 nsin
xn2−x jest ci ˛agiemniesko ´nczone małym dla ci ˛agu
x
n→ x
.•
cos x = sin(
π2− x)
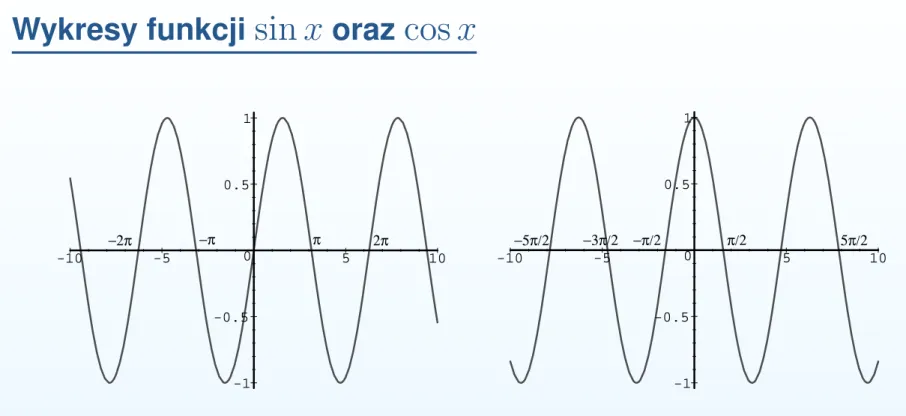
.Wykresy funkcji
sin x
oraz
cos x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -1 -0.5 0 0.5 1 -10 -5 5 10 π 2π −π −2π -1 -0.5 0 0.5 1 -10 -5 5 10 π/2 5π/2 −π/2 −5π/2 −3π/2Funkcje
tg x
,
ctg x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneDefinicja 20. 1.
tg x =
cossinxx2.
ctg x =
cossinxx.Uwaga 21. W literaturze angloj ˛ezycznej u˙zywa si ˛e oznacze ´n
tg x
orazctg x
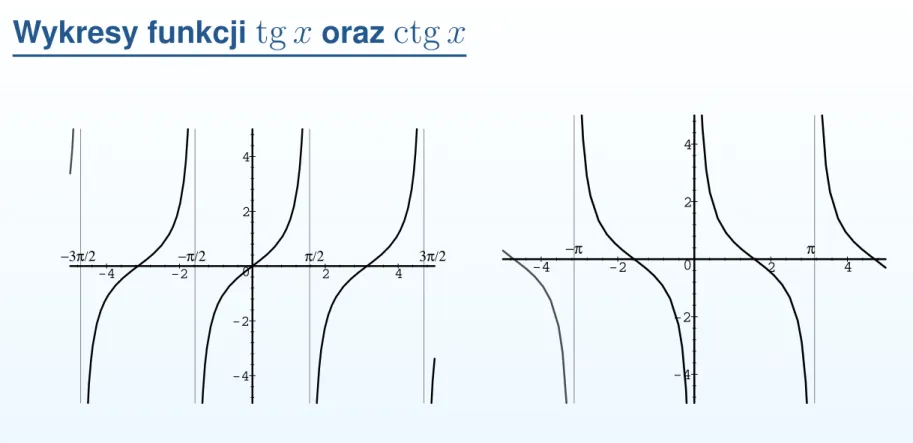
.Własno ´sci funkcji
tg x
ictg x
Twierdzenie 22. 1. Funkcja
tg x
jest ci ˛agł ˛a przyx
6=
π2+ kπ
, za´s funkcjactg x
jest ci ˛agł ˛a przyx
6= kπ
.2. Funkcje
tg x
orazctg x
maj ˛a okresπ
.3. Funkcja
tg x
ro´snie na ka˙zdym z przedziałówWykresy funkcji
tg x
oraz
ctg x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -4 -2 0 2 4 -4 -2 2 4 π/2 3π/2 −π/2 −3π/2 -4 -2 0 2 4 -4 -2 2 4 π −πFunkcje kołowe (odwrotne trygonometryczne funkcje)
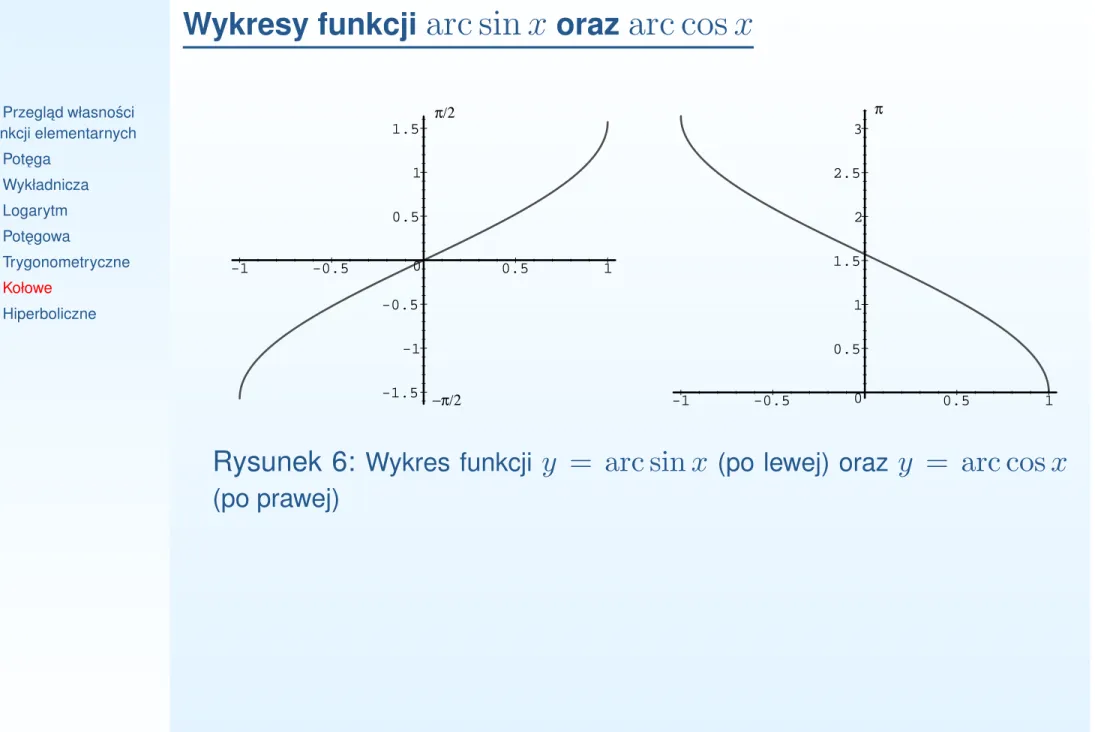
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneDefinicja 23. •
arc sin x : [−1, 1] → [−
π2,
π2]
jest funkcj ˛a odwrotn ˛a dosin x : [−
π2,
π2] → [−1, 1]
.•
arc cos x : [−1, 1] → [0, π]
jest funkcj ˛a odwrotn ˛a docos x : [0, π] → [−1, 1]
.•
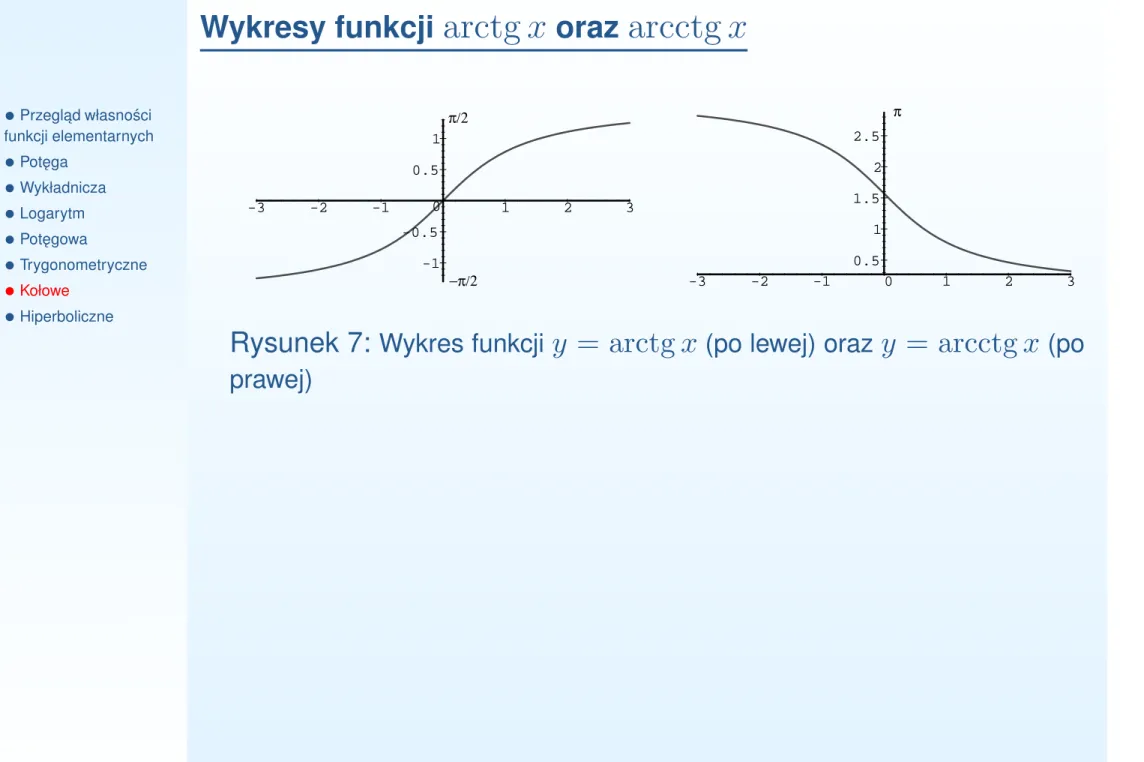
arctg x : (−∞, +∞) → (−
π2,
π
2
)
jest funkcj ˛a odwrotn ˛a dotg x : (−
π2,
π2
) → (−∞, +∞)
.•
arcctg x : (−∞, +∞) → (0, π)
jest funkcj ˛a odwrotn ˛a doctg x : (0, π) → (−∞, +∞)
.Twierdzenie 24. 1. Wszystkie te funkcje s ˛a ci ˛agłe, 2. funkcje
arc sin x
iarctg x
s ˛a rosn ˛ace,Wykresy funkcji
arc sin x
oraz
arc cos x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -1.5 -1 -0.5 0 0.5 1 1.5 -1 -0.5 0.5 1 −π/2 π/2 0 0.5 1 1.5 2 2.5 3 -1 -0.5 0.5 1 πRysunek 6: Wykres funkcji y = arc sin x (po lewej) oraz y = arc cos x
Wykresy funkcji
arctg x
oraz
arcctg x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -1 -0.5 0 0.5 1 -3 -2 -1 1 2 3 −π/2 π/2 0.5 1 1.5 2 2.5 -3 -2 -1 0 1 2 3 πRysunek 7: Wykres funkcji y = arctg x (po lewej) oraz y = arcctg x (po prawej)
Funkcje hiperboliczne
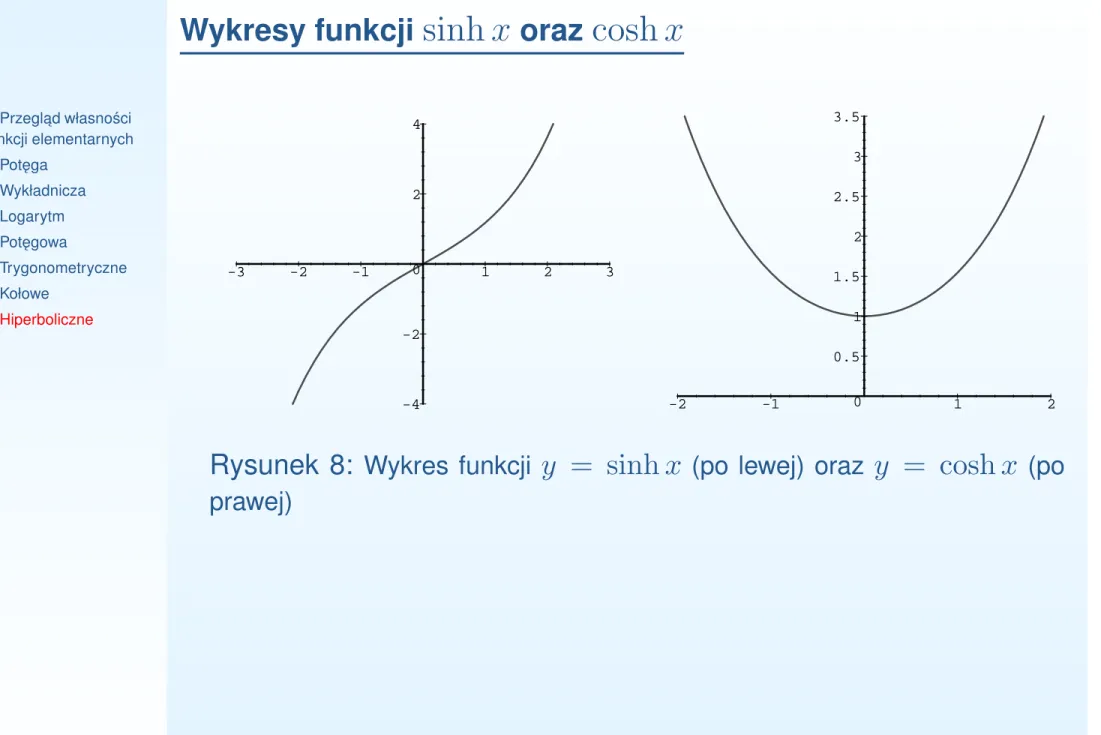
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •HiperboliczneDefinicja 25. 1. Funkcja
sinh =
ex−2e−x nazywa si ˛e sinusem hiperbolicznym2. Funkcja
cosh =
ex+2e−x nazywa si ˛e cosinusem hiperbolicznym 3. Funkcjatgh =
coshsinhxx=
eexx−+e−xe−x nazywa si ˛e tangensem
hiperbolicznym
4. Funkcja
ctgh =
coshsinhxx=
eexx+−ee−x−x nazywa si ˛e cotangensemhiperbolicznym
Twierdzenie 26. Funkcje hiperboliczne s ˛a ci ˛agłe we wszystkich punktach prostej
R
(cotangens hiperboliczny oprócz punktux
= 0
).Twierdzenie 27.
sinh(x + y) = sinh x · cosh y + cosh x · sinh y,
cosh(x + y) = cosh x · cosh y + sinh x · sinh y.
Wykresy funkcji
sinh x
oraz
cosh x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -4 -2 0 2 4 -3 -2 -1 1 2 3 0 0.5 1 1.5 2 2.5 3 3.5 -2 -1 1 2Rysunek 8: Wykres funkcji y = sinh x (po lewej) oraz y = cosh x (po prawej)
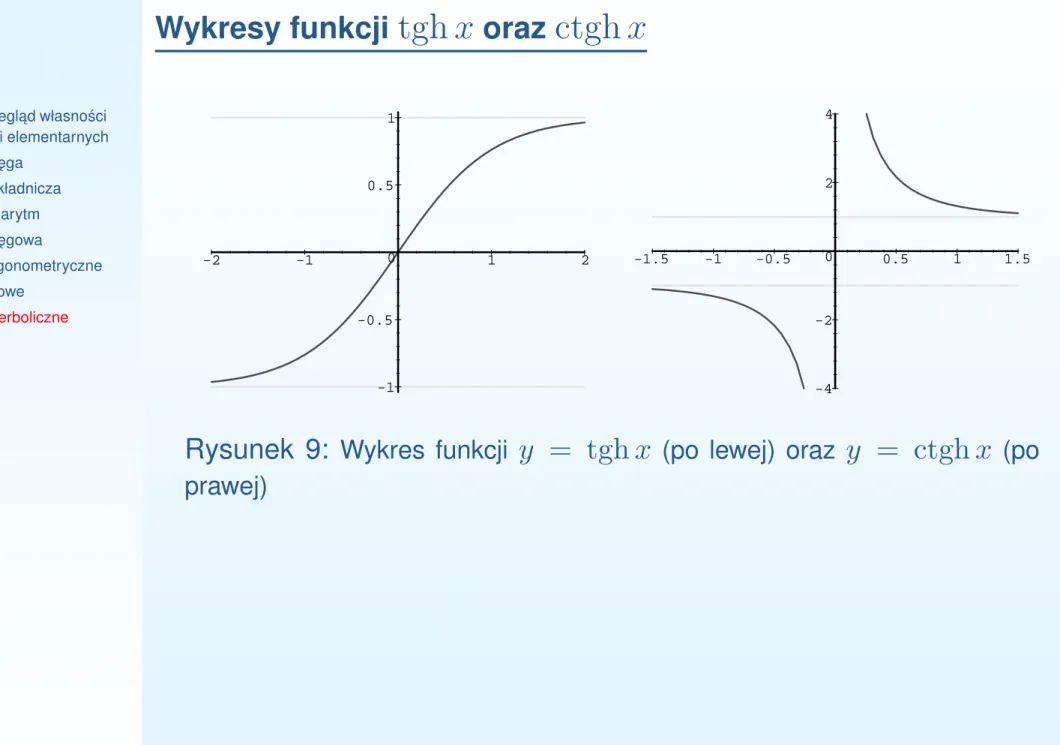
Wykresy funkcji
tgh x
oraz
ctgh x
•Przegl ˛ad własno´sci funkcji elementarnych •Pot ˛ega •Wykładnicza •Logarytm •Pot ˛egowa •Trygonometryczne •Kołowe •Hiperboliczne -1 -0.5 0 0.5 1 -2 -1 1 2 -4 -2 0 2 4 -1.5 -1 -0.5 0.5 1 1.5Rysunek 9: Wykres funkcji y = tgh x (po lewej) oraz y = ctgh x (po prawej)