Podstawy teorii uczenia Podstawy teorii uczenia

Podstawy teorii uczenia Podstawy teorii uczenia

Wykład 4

Włodzisław Duch

Katedra Informatyki Stosowanej UMK Google: W. Duch

Co było Co było

Najprostsze rozproszone pamięci skojarzeniowe.

•BCM, Binarna Pamięć Skojarzeniowa;

•CMM, macierze korelacji, zastosowania do słowników;

•BAM, dwukierunkowa progowa pamięć asocjacyjna.

Co będzie Co będzie

• Prawdopodobieństwa

• Uczenie Bayesowskie

Uczenie Uczenie Uczenie Uczenie

• Chcemy się czegoś nauczyć o strukturze danych, stworzyć model, który potrafi ją analizować.

• W nauce i zastosowaniach technicznych tworzy się modele

parametryczne zjawisk. Są łatwe w interpretacji, ale wymagają teorii i można je zrobić tyko w stosunkowo prostych przypadkach.

Np. prawa fizyki opierają się na takich modelach.

• Empiryczne modelowanie nieparametryczne nie zakłada żadnego modelu, tylko dopasowuje się do danych.

Takie modele dominują w biologii. Uczymy się z danych!

• Mając przykłady = dane treningowe, tworzymy model danych

odpowiadający na specyficzne pytania, oceniając te cechy danych, które mogą się przydać do przyszłych ocen.

• Uczenie = ocena parametrów; paradoksalnie model nieparametryczny ma dużo parametrów, ale nie mających bezpośredniej interpretacji.

Obiekty w przestrzeni cech Obiekty w przestrzeni cech

• Opis matematyczny reprezentuje obiekty O przy pomocy

pomiarów, jakie na nich przeprowadzono, podając wartości cech {O_i} => X(O_i), gdzie X_j(O_i) jest wartością j-tej cechy opisującej O_i

• Atrybut i cecha są często traktowane jako synonimy, chociaż ściśle ujmując “wiek” jest atrybutem a “młody” cechą, wartością.

• Typy atrybutów:

kategoryczne: symboliczne, dyskretne – mogą mieć charakter nominalny (nieuporządkowany), np. “słodki, kwaśny, gorzki”, albo porządkowy, np. kolory w widmie światła,

albo: mały < średni < duży (drink).

ciągłe: wartości numeryczne, np. wiek.

x₂

x₁

x₃ x(O)

Wektor cech X =(x₁,x₂,x₃ ... x_d),

o d-składowych wskazuje na punkt w przestrzeni cech.

Prawdopodobieństwo Prawdopodobieństwo Prawdopodobieństwo Prawdopodobieństwo

Przewidywaniom można przypisać prawdopodobieństwo.

Próbkom X przypisać można K kategorii (klas) C₁ ... C_K

Ogólnie Ci jest stanem którego prawdopodobieństwo chcemy ocenić.

P_k = P(C_k), a priori (bezwarunkowe) prawd. zaobserwowania X  ^Ck

1

1; ( )

K

k

k k

k

P P N C

 N

 



Jeśli nic innego nie wiemy to njabardziej prawdopodobna klasa X to klasa większościowa:

; arg max

m k k

C m P

 

X

Klasyfikator większościowy: przypisuje X do klasy większościowej.

Np: prognoza pogody – jutro taka sama jak dzisiaj (zwykle działa).

Rodzaje prawdopodobieństwa Rodzaje prawdopodobieństwa

Tablica współwystępowania klasa-cecha: P⁽C,r_i⁾⁼N⁽C,r_i)/N

N⁽C, r_i) = macierz,

rzędy = klasy, kolumny = cechy r_i P⁽C, r_i) – prawdopodobieństwo

łączne, P obserwacji obiektu z klasy

C dla którego cecha xri

     

     

     

     

     

1 1 1 2 1 3

2 1 2 2 2 3

3 1 3 2 3 3

4 1 4 2 4 3

5 1 5 2 5 3

, , ,

, , ,

, , ,

, , ,

, , ,

P C r P C r P C r P C r P C r P C r P C r P C r P C r P C r P C r P C r P C r P C r P C r

 

 

 

 

 

 

 

 

P⁽C) to prawd. a priori pojawienia się obiektów z danej klasy, przed wykonaniem pomiarów i określeniem, że xr_i ma jakąś wartość.

To suma w danym rzędzie:  ^, i   

i

P C x r  P C



P⁽xr_i) to prawd że znajdujemy jakąś obserwację dla które cecha xr_i

czyli suma dla danej kolumny.  ^{j, i}  ^{ i }

j

P C x r  P x r



Prawdopodobieństwa warunkowe Prawdopodobieństwa warunkowe

Jeśli znana jest klasa C (rodzaj obiektu) to jakie jest prawdopodobieństwo że ma on własność xr_i ^?

P⁽xr_i|C) oznacza warunkowe prawdopodobieństwo, że znając klasę C ^cecha x będzie leżała w przedziale r_i^.

Suma po wszystkich wartościach cech daje 1:

 ^, i   

i

P C x r  P C



 _i ^|   ^, _i   ^/

P x r C  P C x r P C

P_C⁽x⁾⁼P⁽x|C) rozkład prawd. warunkowego to po prostu przeskalowane prawdopodobieństwo łączne, trzeba podzielić P⁽C,x^)/P⁽C⁾

 i ^|  ¹

i

P x r C 



dla łącznego

prawdopodobieństwa Dlatego mamy:

Reguły sumowania Reguły sumowania

Relacje probabilistyczne wynikają z prostych reguł sumowania!

Macierz rozkładu łącznych prawdopodobieństw: P⁽C, x^{) dla}

dyskretnych wartości obserwacji x, liczymy ile razy

zaobserwowano łącznie N(C,x), skalujemy tak by prawdop.

sumowało się do 1, czyli P(C, x) = N(C,x)/N

   

 

1

1

, ;

| 1;

n

i i

n

i i

P C P C x

P x C













Rząd macierzy P(C, x) sumuje się do:

dlatego P(x|C)=P(C, x)/P(C)

sumuje się do

Kolumna macierzy P(C, x) sumuje się do:

dlatego P(C|x)=P(C, x)/P(x) sumuje się do

   

 

, ;

| 1;

i i

C

i C

P x P C x

P C x









Twierdzenie

Twierdzenie BayesBayesaa

Formuła Bayesa pozwala na obliczenie prawdopodobieństwa

a posteriori P⁽C|x⁾ (czyli po dokonaniu obserwacji) znając łatwy do zmierzenia rozkład warunkowy P⁽x|C^).

Sumują się do 1 bo wiemy, że jeśli obserwujemy x_i to musi to być jedna z

C klas, jak też wiemy, że jeśli obiekt jest z klasy C ^to x musi mieć jedną z wartości xi

Obydwa prawdopodobieństwa są wynikiem podzielenia P⁽C,x_i^).

Formułka Bayesa jest więc oczywista.

Inaczej: H=hipoteza, E=obserwacja

 

 

   

     

     

1;

1

| | 1;

| , /

| , /

C

i i

i

i C

i i

i i i

P C P x

P x C P C x P x C P C x P C P C x P C x P x





 









 

 ^| _i   _i  _i ^|   

P C x P x  P x C P C

   ^|   

| ( )

P E H P H P H E

 P E

Przykład: ryby Przykład: ryby

Chapter 1.2, Pattern Classification (2nd ed)

by R. O. Duda, P. E. Hart and D. G. Stork, John Wiley & Sons, 2000 Automatyzacja sortowania dwóch gatunków ryb, łososia i suma

morskiego, które przesuwają się na pasie sortownika.

Czujniki oceniają różne cechy: długość, jasność, szerokość, liczbę płetw Patrzymy na histogramy.

• Wybieramy liczbę przedziałów, np. n=20 (dyskretne dane)

• obliczamy szerokość przedziału =(x_maxx_min)/n^,

• obliczamy N^(C,r_i) = #sztuk C  {łosoś, sum} w każdym przedziale

r_i ^{= [}x_min+(i-1), x_min+ii=1...n

• prawdopodobieństwo łączne P(C,r_i)=N(C,r_i)/N^{, gdzie} N = liczba ryb Łączne prawdopodobieństwo P(C,r_i) = P(r_i|C)P(C)

Histogramy Histogramy

Rozkład liczby ryb w dwóch wymiarach w 20 przedziałach:l długość i jasność. Zaznaczono optymalne progi podziału.

P⁽r_i|C) przybliża rozkład prawdopodobieństwa dla klasy P⁽x|C^).

Możemy go dokładnie obliczyć tylko w granicy nieskończenie wielu przykładów i podziału na nieskończenie wiele przedziałów.

W praktyce zawsze dzielimy na niewielką liczbę przedziałów.

Przykłady histogramów Przykłady histogramów

Histogramy w 2D: użyteczne ale mogą być trudne do analizy.

SigmaPlot, Origin, pakiety statystyczne np. SPSS je pokazują.

Wyniki zależą od dyskretyzacji ciągłych wartości

http://www.shodor.org/interactivate/activities/Histogram/

Różne aplety tworzące wykresy mają zastosowanie w biznesie http://www.quadbase.com/espresschart/help/examples/

http://www.stat.berkeley.edu/~stark/SticiGui/index.htm Histogramy w kamerach i aparatach cyfrowych:

Histogramy 2D w bioinformatyce Histogramy 2D w bioinformatyce

Popularna prezentacja: dwie zmienne nominalne (geny, próbki) vs.

zmienna ciągła (aktywność) znormalizowana do [-1,+1].

Ekspresja genów dla 16 typów w komórek typu B; kolor zastępuje wysokość słupka histogramu.

•Intensywność = -1 =>

hamowana, jasnozielony

•Intensywność = 0 => normalna, czarny

•Intensywność =+1 => wysoka, jasnoczerwony

Aktywność genu(nazwa genu, typ komórek)

Prawdopodobieństwo warunkowe Prawdopodobieństwo warunkowe

Przewidywania nie mogą być gorsze niż klasyfikator większościowy!

Zwykle możemy określić prawdopodobieństwo warunkowe, mając dane X ^C_k jaka jest najbardziej prawdopodobna klasa?

   ^| 

k k

P X  P X C

Łączne prawdopodobieństwo X dla _k

Czy znajomość prawd. warunkowych wystarczy do przewidywań?

Nie! Ważne jest prawd. posterioryczne:

 ^, k   ^| k   k

P X C  P X C P C

 k ^|   ^, k   ^/

P C X  P X C P X Fig. 2.1, Duda, Hart, Stork,

Pattern Classification (Wiley).

Reguła

Reguła BayesBayesaa

Prawd. posterioryczne są unormowane:

Reguła Bayesa dla 2 klas wynika z prostej równości:

P(X) to bezwarunkowe prawdop.

wylosowania X; zwykle to 1/n, czyli jednakowe dla n probek.

Dla P₁=2/3 i P₂=1/3 robi się:

 

1

| 1

K

k k

P C



 ^X 

     

   

, |

|

i i

i i

P C P C P

P C P C





X X X

X

 i ^|   ^| i     i

P C X  P X C P C P X

Fig. 2.2, Duda, Hart, Stork, Pattern Classification (Wiley).

Decyzje

Decyzje BayesBayesowskieowskie Decyzje

Decyzje BayesBayesowskieowskie

Decyzja Bayesa: mając próbkę X wybierz klasę 1 jeśli:

Prawdopodobieństwo błędu:

Średni błąd:

 1 |   2 | 

P C X  P C X

 |  min   1 |  , 2 |  

P  X  P C X P C X

   ^|   ^|   

P  E P  ^P  P d



  ^X    ^{X X X}

Regułą Bayesa minimalizuje średni błąd P(|X)

Używając reguły Bayesa mnożymy obie strony przez P(X):

 | 1  1  | 2   2

P X C P C  P X C P C

Szansa (

Szansa (LikelihoodLikelihood)) Szansa (

Szansa (LikelihoodLikelihood))

Dane używane są do ocen prawdopodobieństwa.

Bayesowskie decyzje można powiązać z ilorazem szans:

Przy jednakowych prawd. a priori decydują prawdop. warunkowe.

Całkowity błąd przewidywań na skończonej bazie próbek:

   ^| 

P   P 

X

X

Założenie: P(X) daje się ocenić z częstości występowania X.

       

   

   

 

1 1 2 2

1 2

2 1

| |

|

|

P C P C P C P C

P C P C

P C P C



  

X X

X X

X

Fig. 2.3, Duda, Hart, Stork, Pattern Classification (Wiley).

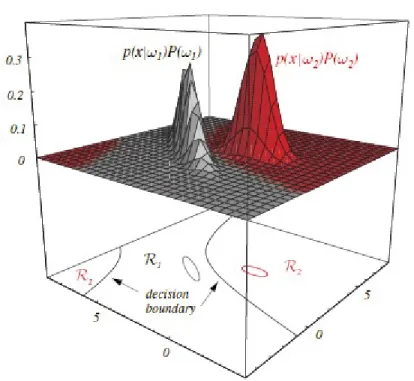
Regiony decyzji w

Regiony decyzji w 2D 2D Regiony decyzji w

Regiony decyzji w 2D 2D

Gaussowskie rozkłady prawd warunkowych dla obu pomiarów (długość, jasność):

Regiony decyzji w 2D są hiperboliczne, regiony w R₂ są rozłączne.

Elipsy pokazują stałe wartości P_k(X).

Fig. 2.6, Duda, Hart, Stork, Pattern Classification.

Kwiatki Kwiatki

Mamy dwa rodzaje Irysów:

Irys Setosa oraz Irys Virginica

Długość liści określamy w dwóch przedziałach, r₁=[0,3] cm i r₂=[3,6] cm.

Dla 100 kwiatów dostajemy następujące rozkłady (Setosa, Virginica):

36 4 ( , )

8 52 N C r  

  

 

Prawdopodobieństwa łączne i warunkowe różnych kwiatów Irysów:

0.36 0.04 ( , )

0.08 0.52

P C r  

  

 

Stąd

   

   

1 2

1 2

40, 60

44, 56

N C N C

N r N r

 

 

   

   

1 1

2 2

0.4; 0.44

0.6; 0.56

P C P r

P C P r

 

 

 ^|   ^,   ^{/ 0.90 0.10 ;}  ^|  ^{0.82 0.07}

0.13 0.87 0.18 0.93

P r C P C r P C   P C r  

      

   

wiersze kolumny

Przykład Przykład Przykład Przykład

C₁ to stan natury, choroba “denga”, a C₂ to brak dengi, czyli zdrowie.

Załóżmy, że prawdopodobieństwo zachorowania to P(C1)=1/1000

Załóżmy, że test T ma dokładność 99%, czyli wynik dodatni dla chorego na dengę ma prawdopodobieństwo P(T=+| C₁) = 0.99, a negatywny dla zdrowych ludzi to również P(T=| C2) = 0.99.

Jeśli test wypadł pozytywnie, jaka jest szansa, że masz dengę?

Jakie jest prawdopodobieństwo P(C1|T=+)?

P(T=+) = P(C1,T=+)+P(C2,T=+) = P(T=+|C1) P(C1)+P(T=|C2) P(C2)

= 0.99*0.001+0.01*0.999=0.011 P(C1|T=+)=P(T=+| C1)P(C1)/P(T=+)

= 0.99*0.001/0.011 = 0.09, or 9%

Kalkulator Baysowski jest tu: http://StatPages.org/bayes.html

Podsumowanie Podsumowanie Podsumowanie Podsumowanie

Chcemy prawd. posterioryczne:

Minimalizację błędów można robić na wiele sposobów:

Można wprowadzić koszty różnych typów błędów i minimalizować ryzyko używając Bayesowskich

procedur. Bezpośrednie oceny prawdopodobieństw dla X o więcej niż 2 wymiarach wymagają zbyt wielu danych, dlatego potrzebny jest model M() minimalizujący błędy.

     

 

| | ^{i i}

i

P C P C P C  X P

X X

   

1 1

1 ^K _ii; ^K _i | _i

i i

E P E P C K

 

     

X

X X

Likelihood x Prior



Evidence

gdzie K_i(X) = 1 dla X z klasy C_i, lub 0 dla innych klas.

Ocena modelu: dwa typy błędów Ocena modelu: dwa typy błędów Ocena modelu: dwa typy błędów Ocena modelu: dwa typy błędów

Macierz pomyłek (konfuzji)

 prawda|przewidziane ^{TP FN}

FP TN

P P

P P P

 

 

 

 

    

Notacja często używana w aplikacjach medycznych:

P_ sukces, true positive (TP); P_P_ ułamek TP do wszystkich P+;

P_ sukces, true negative (TN); P_P_ ułamek TN do wszystkich P_-

Dokładność = P_ + P_ = 1Błąd = 1  P_  P_

P_ fałszywy alarm, false positive (FP); np. zdrowy uznany za chorego

P_ strata, false negative (FN); np. chory uznany za zdrowego.

Co dalej?

Co dalej?

• Samoorganizacja – uczenie bez nadzoru

• Mapowanie topograficzne i mózgi

• SOM – Samoorganizująca Się Mapa

• Growing Cell Structures

• Przykłady zastosowań

• Przykłady wizualizacji

• Samoorganizacja i mapy ekwiprobabilistyczne

• Uczenie konkurencyjne.

• Gaz neuronowy.

• Skalowanie wielowymiarowe i redukcja wymiarowości problemu.

Koniec wykładu 4 Koniec wykładu 4