Postać algebraiczna liczby zespolonej

(1)

Postać algebraiczna liczby

zespolonej

Autorzy:

Agnieszka Kowalik

(2)

Postać algebraiczna liczby zespolonej

Autor: Agnieszka Kowalik

DEFINICJA

Definicja 1: Postać algebraiczna liczby zespolonej

Niech , gdzie będzie dowolną liczbą zespoloną. Zauważmy, że liczbę możemy zapisać następująco:

Wówczas oznaczając , oraz otrzymujemy postać algebraicznąpostać algebraiczną (Hamiltona, kanoniczną) liczby zespolonej

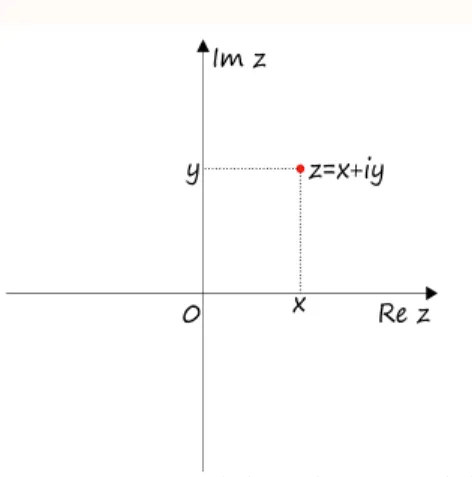
Rysunek 1: Interpretacja geometryczna liczby zespolonej w postaci algebraicznej

Niech będzie liczbą zespoloną w postaci algebraicznej. Przypomnijmy, że liczbę nazywamy częścią rzeczywistączęścią rzeczywistą liczby i oznaczamy sybolem , zaś liczbę nazywamy częścią urojonączęścią urojoną liczby i oznaczamy symbolem .

PRZYKŁAD

Przykład 1:

Dla liczby zespolonej częścią rzeczywistą jest liczba , a częścią urojoną liczba .

Niech oraz będą liczbami zespolonymi. Liczby i , jako uporządkowane pary punktów, są równe wtedy i tylko wtedy, gdy oraz . Stąd, zapisując liczby i w postaci algebraicznej jako oraz

otrzymujemy, że wtedy i tylko wtedy, gdy oraz .

Postać kanoniczna liczby zespolonej umożliwia dodawanie i mnożenie liczb zespolonych tak samo jak wielomianów, tzn. podobny do podobnego (dla dodawania) i każdy z każdym (dla mnożenia), w przypadku mnożenia pamiętając o warunku . Przy dzieleniu przez liczbę zespoloną mnożymy dzielną i dzielnik przez , otrzymując w mianowniku liczbę rzeczywistą.

z = (x, y)

x, y ∈ R

z

z = (x, y) = (x, 0) + (0, y) = (x, 0) + (y, 0) ⋅ (0, 1).

x = (x, 0) y = (y, 0)

i = (0, 1)

z

z = x + iy.

z = x + iy

x

z

Rez

y

z

Imz

z = 3 − i

Rez = 3

Imz = −1

= ( , )

z

1

x

1

y

1

z

2

= ( , )

x

2

y

2

z

1

z

2

=

x

1

x

2

y

1

=

y

2

z

1

z

2

z

1

=

x

1

+ i

y

1

=

+ i

z

2

x

2

y

2

z

1

=

z

2

Re = Re

z

1

z

2

Im = Im

z

1

z

2

= −1

i

2

z = x + iy

x − iy

(3)

PRZYKŁAD

Przykład 2:

Niech , . Mamy:

DEFINICJA

Definicja 2: Sprzężenie liczby zespolonej

Niech , gdzie . SprzężeniemSprzężeniem liczby nazywamy liczbę daną wzorem

Rysunek 2: Sprzężenie liczby zespolonej

TWIERDZENIE

Twierdzenie 1: Własności sprzężenia liczb zespolonych

Niech . Prawdziwe są następujące własności:

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

z = 2 − 3i w = −1 + i

z + w = 2 − 3i − 1 + i = (2 − 1) + (−3i + i) = 1 + (−2i) = 1 − 2i.

z − w = 2 − 3i − (−1 + i) = (2 − (−1)) + (−3i − i) = 3 − 4i.

z ⋅ w = (2 − 3i) ⋅ (−1 + i) = −2 + 2i + 3i − 3(i = −2 + 5i − 3(−1) = −2 + 3 + 5i = 1 + 5i.

)

2

=

= − + i.

z

w

−1 + i

2 − 3i

(−1 + i)(−1 − i)

(2 − 3i)(−1 − i)

−2 − 2i + 3i + 3i

2

1 + i − i − i

2

−5 + i

₂

5 ₂

1 ₂

z = x + iy

x, y ∈ R

z

z¯

= x − iy.

z¯

z, , ∈ C

z

1

z

2

a)

¯

z

¯¯¯¯¯¯¯¯¯¯¯¯¯1

+

z

2¯

= + ;

z

¯ z

1

¯

2

c)

z

¯¯¯¯¯¯¯¯¯¯¯1

⋅

z

2¯

= ⋅ ;

z

¯ z

1

¯

2

e)

( )

¯ ¯¯¯¯¯¯¯¯¯

z

= z;

g) z − = 2iImz.

z¯

b)

z

¯¯¯¯¯¯¯¯¯¯¯¯¯¯1

−

z

2¯

= − ;

z

¯ z

1

¯

2

d)

( )

z

1

=

, dla

≠ 0;

z

2 ¯¯¯¯¯¯¯¯¯¯¯¯¯¯

_z

1

¯

z

¯

2

z

2

f) z + = 2Rez;

z¯

(4)

Data generacji dokumentu: 2019-04-15 04:31:55

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=5465768a8f5ea276c56a42bf16fc9a16