Transmisyjna Mikroskopia elektronowa
Sławomir Kret,
kret@ifpan.edu.pl
Instytut Fizyki PAN
Transmisyjna Mikroskopia Elektronowa TEM
(Transmission Electron Microscopy)
informacje o defektach i składzie chemicznym z wnętrza materiału rozdzielczość w zależności od trybu pracy
Aktualny rekord w eksperymentalnym mikroskopie 0.05 nm (50 pm)
Skaningowa Mikroskopia Elektronowa (SEM)
topografia powierzchni
sklad chemiczny powierzchni
Geneza TEM
W 1923 Prince Louis de Broglie postulował falową naturę materii.
W 1927 Hans Bush pokazał, że cewki magnetyczne mogą ogniskować
wiązkę elektronową w taki sam sposób, jak szklane soczewki światło.
W 1927 C.J. Davisson i L.H Germer oraz G. P. Thompson i A. Reid
niezależnie zademonstrowali dyfrakcję elektronową wykazując falową naturę
elektronów.
7 kwietnia 1931 Ernst Ruska i Max Knoll otrzymali pierwszy obraz TEM
wykorzystując dwie soczewki magnetyczne.
Budowa transmisyjnego mikroskopu
elektronowego
Wyrzutnia elektronów (działo elektronowe)
Kondensor – układ soczewek skupiających elektrony Komora preparatu
Obiektyw – tworzy obraz: rzeczywisty, odwrócony, powiększony
Ekran – materiał święcący w wyniku bombardowania elektronami, np. siarczek cynku
Soczewki pośrednie i projekcyjna – powiększają i rzutują obraz utworzony przez obiektyw.
System rejestracji obrazu – klisza fotograficzna, kamera TV, matryca CCD Detektory promieniowania rentgenowskiego, filtry energii, spektrometry strat energii elektronów. Ernst August Friedrich Ruska (1906 -1988) Nobel 1986
Jeol 2000EX IF-PAN (1989) 200kV Rozdzielczość 0.27 nm
Rozdzielczość ograniczona przez soczewki
Przełom w TEM
działo z emisja polową +korekcja aberracji sferycznej
Jeol 2000ex IF-PAN 0.25 nm
LaB
6HRTEM imaging of atoms at sub-Ångström resolution, O'Keefe et al. J Electron Microsc (Tokyo).2005; 54: 169-180
Microsc. Microanal.,Vol.9(Suppl.3),038 (2003)
G. Benner, M. Matijevic, A. Orchowski, B. Schindler* , M. H., P. Hartel Carl Zeiss SMT’s new sub-Angstrom UHRTEM 0.25 nm 0.1 nm 0.06 nm
Napięcie przyspieszające [kV] [nm] (nm) relatywistyczna prędkość (x108 m/s) 100 0.00386 0.00370 1.644 200 0.00273 0.00251 2.086 300 0.00223 0.00197 2.330
Rozdzielczość a długość fali
Jeol 2000EX IF-PAN (1989) 200kV 0.27 nm
Rozdzielczość ograniczona przez soczewki
FEI Titan+ Cs + monochromator 300kV ( =2 pm) 0.07 nm (70 pm)
Rozdzielczość ograniczona przez szczątkową aberrację chromatyczną,
Oddziaływanie wysokoenergetycznych elektronów z atomem
- energia 100-1000 eV
1. Nie rozproszone
2. Nisko kątowe rozpraszanie elastyczne
3. Wysoko kątowe rozpraszanie elastyczne
4. Wstecznie rozproszone
5. Rozproszenie nieelastyczne na zewnętrznej powłoce
6. Rozproszenie nieelastyczne na wewnętrznej
Padający elektron
elektron Augera
wybity elektron (jonizacja)
poziom próżni poziom Fermiego
charakterystyczny foton X
dziura Elektron ze stratą
energii
Oddziaływanie wysokoenergetycznych elektronów z ciałem
stałym – rozpraszanie nieelastyczne
Sygnały produkowane przez sondę elektronową w cienkim
krysztale wykorzystywane do tworzenia obrazów i/lub
spektroskopii
padająca wiązka elektronowa 10m ….0.1 nm
elektrony przechodzące bez rozproszenia
elektrony rozproszone nieelastycznie EELS elektrony rozproszone elastycznie
DYFRAKCJA
CTEM, SAD, HRTEM, Z-contrast
Cienki preparat t=5-200 nm
ciepło
wstecznie rozproszone elektrony
elektrony wtórne elektrony Auger’a Fotony widzialne katodoluminescencja Promieniowanie X EDX
Dlaczego elektrony są tak interesujące ?
Rozpraszanie na:
Średnia droga
swobodna [nm]
Długość absorpcji
[nm]
Neuutrony
jądrach
10
710
8X-rays
elektronach
10
310
5elektrony
potencjale
10
10
2Bardzo silne oddziaływanie z materią
Sygnał od 1 atomu w próbce dla elektronów jest
Image from:Electron Microscopy in Solid Stage Physics H.Bethge and J. Heydenreich , Elesevier 1987
Kąt padania wiązki jonów 1-25°, ale <5 ° pozwala uniknąć selektywnego trawienia Napnięcie przyspieszające 4-9kV (200V- 8kV) czas 1-48h
Jony Argonu, chłodzenie ciekłym azotem pośrednio, ( strumieniem gazu obojętnego ) próżnia 10-5 Torr (10-3 Torr podczas trawienia)
Wykonanie przekroju poprzecznego : 10-50 nm grubości
Trawienie jonowe powoduje defekty radiacyjne i amorfizuje powierzchnie Ograniczenie uszkodzeń poprzez:
- niższe napięcie , zmniejszanie kąta padania wiązki jonów, chłodzenie preparatu
Precision Ion Polishing System (PIPS™) na wyposażeniu IF-PAN
Dzialła jonowe 100V - 6KV
kąty 0º-10º
Wideo mikroskop z „zoomem” Chłodzenie ciekłym azotem
Obraz TEM Obraz dyfrakcyjny Socz. Proj. probka Przysłona kontrastu Soczewki pośrednie obraz 1 objektyw Pł. Ogniskowa Przys.Selec. obraz 2
k
ik
d2
ghkl
The Ewald sphere construction
1/d
hkln
= 2 d
hklsin
1/
The Ewald sphere for high
energy electrons
Diffraction occurs when the Ewald sphere intersects a reciprocal lattice nodes
For 200 kV electrons, 1/λ = 1/0.00273 nm = 366 nm-1
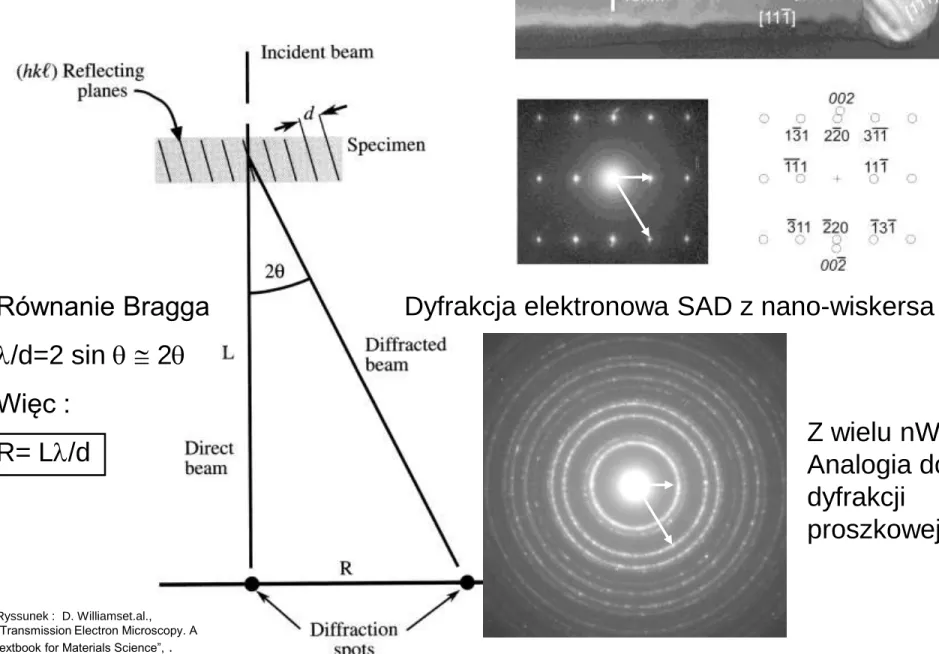
Równanie Bragga
/d=2 sin 2 Więc :
R= L/d
Dyfrakcja elektronowa SAD z nano-wiskersa ZnTe
Z wielu nW Analogia do dyfrakcji
proszkowej X-ray
Dyfrakcja elektronowa
Fot. P.Dluzewski, S.Kret IF-PAN Ryssunek : D. Williamset.al.,
“Transmission Electron Microscopy. A textbook for Materials Science”,.
BF
DF
DF
Diffraction contrast: bright and dark field
Picures from : D. Williams et.al., “Transmission Electron Microscopy. A textbook for Materials Science”,.
Two-beam conditions for Si near 001 zone axis
Kontrast dyfrakcyjny: jasne i ciemne pole
Krystality Pd o wymiarach 5-15 nmPERFECT CRYSTALS
Thickness contours
For a wedge specimen, the separation of the fringes in the image is determined by the angle of the wedge and the extinction distance, ξg.
. Photo : S.kret IFPAN
– Considers many beams
– Intensity in one or more diffracted beams can be large in comparison with transmitted beam
– Multiple scattering allowed
– “Absorption ” (loss of electrons) allowed
– Can explain intensity accurately what is impossible with kinematical theory - However still phenomenological treatment of inelastic scattering
Dynamical theory of diffraction contrast
Kinematical approximation
– Intensity of diffracted beam is small – Single scattering event
So..
Bloch waves in silicon crystal
in two beam and multi beam conditions
220 excited s~=0
Perfect 001 zone axis orientation proper method for perfect crystal but complicated to use in the case of defected or deformed crystal
g g g g g g g i z is i dz d z is i i dz d 0 0 0 0 0 2 exp 2 expThe Howie-Whelan equations for two beams and perfect crystal
Description of the amplitude of diffracted 0 and g as a function of z is given by:
Integration over the entire thickness gives the 0 and g at exit surface of the specimen The bright-field intensity is then given by 00*
The dark-field intensity is then given by gg*
g B F cos c g V
Vc the volume of unit cell
the Bragg angle
the electron wavelength Fg the structure factor The extinction distance is given by:
K
iK
Ds
gS
g<0
Excitation error
or
Deviation parametr „s
g”
ghkl„Absorption” high-angle scattering ( elastic and/or inelastic)
can be accounted for by replacing 1/
by 1/+i/
’’” a parameter ’ which is usually about 0.1 is really a fudge factor that modifies H-W equations to fit the experimental observations „
Analytical solution of the Howie-Whelan equations
2 2 2 2 * 2 ) ( sin eff eff g g g g S tS Ig 2 2 1 g eff s S
where
CRYSTAL WITH DEFECTS
Intuitive description of diffraction contrast of dislocation
Bragg conditions locally satisfied
Atomic plane bending Axial BF
TB-DF
Photo :P.Dłużewski IF-PAN
Sample ł. GELCZUK et.al. WEMiF ,Wrocław
The Two-Beam Dynamical Approximation
Howie-Whelan equations for two beams
With : column approximation , absorption , crystal deformation
g g g g g g g g i i R g z s i i i dz d R g z s i i i i i dz d ' 0 0 0 ' 0 ' 0 ' 0 0 0 1 ) ( 2 exp 1 ) ( 2 exp 1 1 R
Is the displacement fieldThe column approximation
At the bottom surface of the sample, the contribution of the electrons to the intensity on a point in the exit surface of the sample is coming at most from an area which is at the base of a cone.
=0.0037 nm 100 kV
b ~ 0.01 radians t= 100 nm
Diameter of the column 2nm
A
B
c
2
BSpecimen
Top
Bottom
t
t
A
B
c
0 0 0 dz dR dy dR dx dRContrast from single dislocation
The quantity gR in H-W equantions depend on the scalar gb or gbu
as well as in kinematical approximation where the amplitude of diffracted beam is :
r 2 b R ) 1 ( 4 2 cos ln ) 1 ( 2 2 1 ) 1 ( 4 2 sin 2 1 b b b u r RIn isotropic elasticity, the displacement R near a dislocation at a point (r,) is given as
for screw dislocations and
for edge dislocations
u is dislocation line , b Burgers vector ,
Poisson’s ratio
t g g i g R sz dz i 0 )) ( 2 exp( where t is the thickness of the foil z
x dz
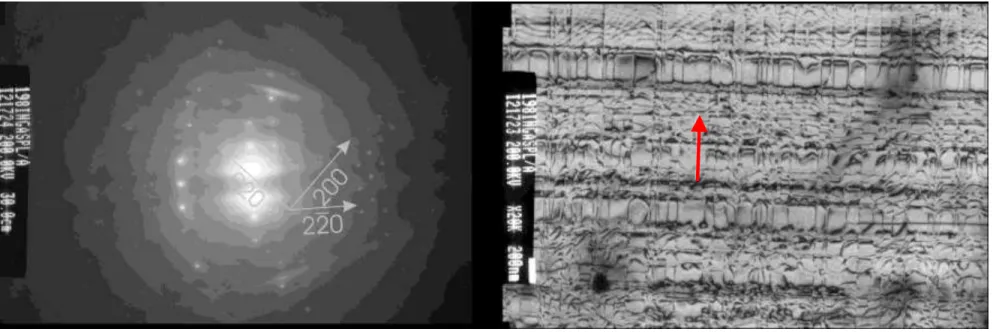
Kontrast dyfrakcyjny: Warunek dwuwiązkowy
Siatka dyslokacji niedopasowania GaAs/In0.07GaAs
Foto :P.Dłużweski IF-PAN
Próbka: ł. GELCZUK et.al. WEMiF ,Wrocław
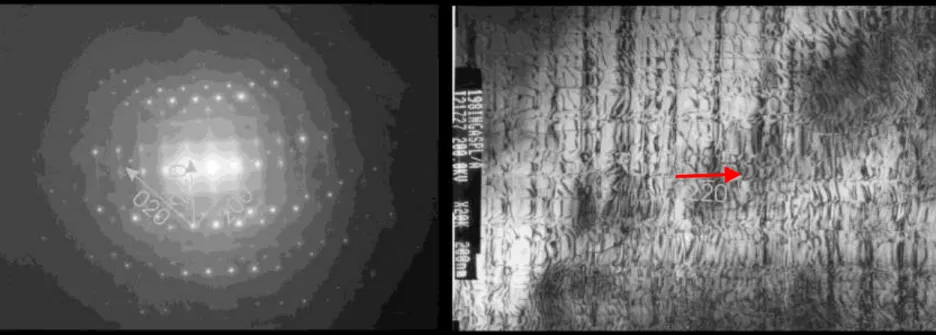
Kontrast dyfrakcyjny: Warunek dwuwiązkowy
Siatka dyslokacji niedopasowania GaAs/In0.07GaAs
Foto :P.Dłużweski IF-PAN
Próbka: ł. GELCZUK et.al. WEMiF ,Wrocław
Foto :P.Dłużweski IF-PAN
Próbka: ł. GELCZUK et.al. WEMiF ,Wrocław
Dyslokacja znika jeśli
g
b
0
Kontrast dyfrakcyjny: Warunek dwuwiązkowy
In 1967 Head showed that under g·b = 0 dynamical conditions in bright feld screw dislocation in -CuZn still exhibits significant and complex contrast. invisibility criterion can be not valide for anisotropic materials
Single dislocation in
Al - 8%at Li
MicroScope for Windows
(Prof. Veli-Tapani Kuokkala , Tampere University of Technology)
based on the dynamical two-beam theory
column approximation.
The program calculates and displays brightfield and darkfield images of dislocations and stacking faults.
Coherently strained heterostructures
Self-organized Si/SiGe QDs
Photo M.Zak IFPAN
M.Zak at al. . Mikron 2008 in press
20nm
dome
[011]
pyramid
Pyramid and dome shapes and dimensions of the SiGe islands
Determinatin of the strain in coherently strained Si/SiGe QD
using the two beam diffraction contrast simulation
Finite element model of dome shape QDs
3D FE mesh nodes on the surface of model of dome shape SiGe QD
Calculated colore coded
u
x displacement of the surface nodes FE coordinatesCrystal cooordinates
Cross-section by 3D FE model of QD x z t z 0=1, g=0 0<1, g>0
u
xg=220
g=220
A C B B' A' C' Soczewka obiektywu Przyslona kontrastu
Równolegla wiązka elektronów
P.ogniskowa
Plaszczyzna obrazu Syntylator lub film wlókna optyczne
-g O g
Plaszczyzna obiektu
Cienka folia t=5-30nm
Tryb pracy HRTEM
Zasada tworzenia obrazu HRTEM
(selekcja wiązek ugiętych na obrazie dyfrakcyjnym)
Interferencja 2 wiązek
(a) (b)
HRTEM GaAs <110>
Zn Te monowarstwa 0.3 nm 7 wiązek Rozdzielczość 0.27 nm13 wiązek
Rozdzielczość 0.16 nmSYMULACJA HRTEM :
ETAP I
wysokoenergetyczne elektrony w krysztale
weak-phase-object
propagacja z
metoda " multislice " : podział grubego kryształu na plasterki "weak-phase-object aproximation"
Cowley and Moodie (1957)
p r) ( ) ( ) ( ) ( 1 1 1 n r n r qn r n
z 0 V x y z dz E e i r qn ( ) exp ( , , ) 1 z y x n 2 2 2 1 ) ( (r) exp -ikz p Funkcja "przezroczystości" plasterka (n+1)
Propagator
http://cimesg1.epfl.ch/CIOL/ems.html by P.Stadelman Internetowy symulator TEM
GaAs kierunek wiązki padającej <110>
Amplitudy wiązki pierwotnej i główne wiązki ugięte
(bez absorpcji)
SYMULACJA HRTEM :
ETAP II
elektrony w układzie optycznym mikroskopu
przybliżenie nieliniowe formowania obrazu
w oświetleniu częściowo koherentnym K.Ishizuka 1980 Uwzględnia aberracje układu optycznego mikroskopu
GaAs <110> Zone axis In
0.5Ga 0.5As <110> Zone axis
Symulacje HRTEM 200 kV LaB6
Grub
ość
[nm]
GaAs/Ga
0.65In
0.35As 23ML
x=0.35
a/a=0.027
naprężenie ~ 3GPa
Kontrast dyfrakcyjny w rzucie płaskim [001] Pseudo heksagonalna sieć kropek
Średnia odległość ok. 30 nm
LPS-ESPCI
Przekrój poprzeczny
Elektrony w kierunku <110>
Choices of the images and ROI
LPS-ESPCI
Pomiar rozkładów dystorsji sieci na
obrazach HRTEM
a
x=13.25 pixels
a
z=18.66 pixels
Lokalne dystorsje sieci
x
u
x x
y
u
y y
Kret S. et al. 1999 J.Appl Phys. 86 , 21
Rozkład indu w wyspie
GaAs/Ga
0.65In
0.35As 23ML
na podstawie analizy
HRTEM i modelowania
FE
Ucieczka indu do zrelaksowanej części wyspy !
H. Kirmse, W. Neumann, Humboldt-Universität zu Berlin
Spektrum EDX
Metody spektroskopowe
FEG-EDX
Liniowy profil składu
nanodrut ZnTe/katalizator
E.Janik at al..Nanotechnology, 18,2007, 475606,
ZnTe Au-Ga+??
Analiza strat energii elektorów rozproszonych nieelastycznie EELS
Spektroskopia strat energii elektronów
i mapowanie składu chemicznego
Takie informacje mogą być uzyskane w skali nanometrycznej
ELNES
Extender fine structure (EXELFS) - atom-specific radial distribution of
JEOL 2000EX P..Dłużewski, S.Kret, , A. Szczepańska IF-PAN 2005
115 nm
240 nm 45 nm
JEOL 2000EX S.Kret, P..Dluzewski , A. Szczepańska IF-PAN 2005
5 nm
wydzielenia koherentne Rozmiar 3.5-4.5 nm Kształt : „fasetki” 111
Tecnai G2 F20 S-Twin Cs corrected GIF-EELS S.Kret, A. Szczepańska ,Y. Lefraisim, M. Hytch CEMES 2005 r Tuluza
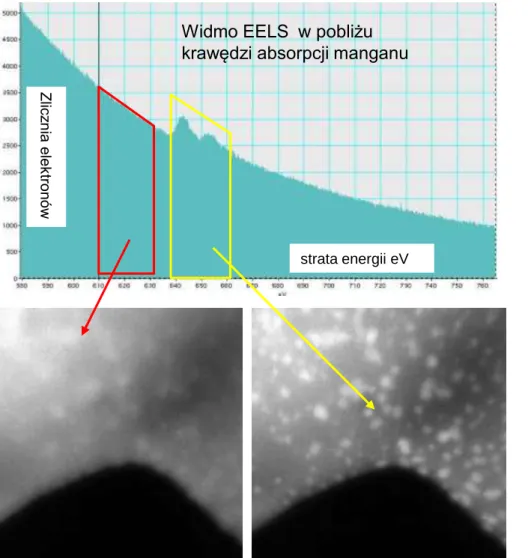
Mapa rozkładu manganu wydzielenia 3-5 nm średnicy
Widmo EELS w pobliżu krawędzi absorpcji manganu
Z lic zni a el ek tr on ów strata energii eV
Obrazy przed i po krawędzi absorbcji
Ga
EELS kolumny atomowej
1.4Å
As
Z-contrast STEM
Z=31
Z=33
Zródło: S. J. Pennycook,“Structure Determination through Z-Contrast Microscopy,”
p. 173 in Advances in Imaging and Electron Physics, Vol 123, ed. by P. G. Merli, G. Calestani, and M. Vittori-Antisari, 2002
RAFAL E. DUNIN-BORKOWSKI et. al. MICROSCOPY RESEARCH AND TECHNIQUE 64:390–402 (2004)
Holografia elektronowa (niskiej rozdzielczości)
precyzyjne pomiary zmiany fazy fali elektronowej
wizualizacja lokalnych pól magnetycznych i elektrycznych,
W.D.Rau et. al, phys. Stat. Sol. (b) 222 , 213 (200)
Nanocząski FeNi, wiry magnetyczne
Tranzystory 0.3m NMOS i PMOS Amplituda i faza
Problem rzutu i uśredniania
I dużo więcej………
Np. +dyfrakcja………
Słabe punkty TEMu
Konieczność wykonania preparatu zniszczenie materiału
Słabe próbkowanie
lokalne informacje tylko z obszarów przezroczystych dla elektronów a jednak około 0.1-0.5 mm2 dla najlepszych preparatów
Artefakty preparatyki
- relaksacja naprężeń w cienkiej folii - amorfizacja, defekty radiacyjne
Zniszczenia radiacyjne elektronami próbka przestaje być reprezentatywna
- jonizacja i niszczenie wiązań chemicznych
- nagrzewanie i dyfuzja składników w słabo przewodzących próbkach - wybijanie lub przesuwanie atomów, rozpylanie
Wysokie koszty aparatury, pracochłonne przygotowanie preparatów
Skomplikowana „klawiszologia” i interpretacja danych wyobraźnia i wiedza mikroskopisty (ciągle potrzebny)
- J.Kozubowski, Metody transmisyjnej mikroskopii elektronowej, Wydawnictwo Śląsk, Katowice 1975.
- Spence, J. C. H., “Experimental High Resolution Transmission Electron Microscopy”, North-Holland, Amsterdam, Holanda, 1994.
- Williams, D. B. y Barry Carter, C., “Transmission Electron Microscopy. A textbook for Materials Science”, Plenum Press, New York, USA, 1996.