Wytrzymao materiaw.

2.Wytrzymałość materiałów

2.1 Ściskanie i rozciąganie prętów

2.1.1

Obliczyć o ile wydłuży się pod własnym ciężarem pręt o długości l, jeżeli wykonany jest z aluminium o gęstości ρ = 2,6 g/cm3 _{i module Younga E = 64 MPa.}

y dx x l x 2.1.2

Dla prętów pokazanych na rysunkach obliczyć wydłużenie całkowite. Dla przypadku C) wyznaczyć również przemieszczenia punktów A i B. Moduł Younga dla wszystkich prętów przyjąć równy E. Dane: F, E, d ,a ,l A) φ2d _φ1,5d l l F B) l/2 φ2d l l F 2F φ1, 5d C) l l/2 l l

φ3a φ2a φ3a

2.1.3

Obustronnie utwierdzony pręt o przekroju kołowym (przedstawiony na rysunku) oziębiono o

∆t°C. Obliczyć reakcje ścian oraz naprężenia w prętach, jeżeli liniowy współczynnik rozszerzalności wynosi α, a moduł Younga jest równy E. Pręt dodatkowo obciążono siłą 7P zaznaczoną na rysunku.

(Termiczne wydłużenie liniowe opisuje zależność ∆l=α∆tl)

7P

φd φ2d

R1=? R2=?

l l

2.1.4

Obustronnie utwierdzony pręt o przekroju kołowym (przedstawiony na rysunku) obciążono siłą Q a następnie ogrzano. Obliczyć o ile ogrzano ten pręt, rekcję R2 a także naprężenia w

prętach, jeżeli reakcja jednej ze ścian po ogrzaniu wynosi 2Q; liniowy współczynnik

rozszerzalności jest równy α, Moduł Younga dla pręta przyjąć równy E.

Q φa φ1, 5a R₁=2Q R2=? l l 2.1.5

Pręt o przekroju kołowym obciążony jest siłami P i 2P jak przedstawiono na rysunku. Wyznaczyć reakcję ścian. Szerokość szczeliny wynosi δ a moduł Younga dla materiału z którego wykonany jest pręt E.

L δ 2P P L L φ2d φd 2.1.6

Filar mostu w całości ma być zanurzony w wodzie. Jak musi się zmieniać przekrój poprzeczny tego filaru wykonanego z betonu o gęstości ρ, aby naprężenia w dowolnym przekroju były równe wytrzymałości betonu na ściskanie kc. Przyjąć że górna powierzchnia

2.1 Zginanie belek

2.2.1

Dla belek przedstawionych na rysunkach sporządzić wykresy siły tnącej (T) oraz momentu gnącego (Mg) a) 2a _a 3a F 2F B A b) 2a a 3a F M = 2Fa B A c) M = 0,5qa2 a a 2a A M = 0,5qa2 q B 2.2.2

W celu zbadania wpływu naprężeń na własności magnetyczne ciał stosuje się próbki w kształcie pasków materiału o przekroju prostokątnym w układzie jak na rysunku. Jaką wartość muszą mieć siły F aby zbadać próbkę w zakresie do granicy plastyczności (200MPa), jeżeli próbki mają długość L = 9 cm, szerokość b = 1 cm i grubość h = 0,3 mm. W jakim obszarze można przeprowadzać badania.

l/3 l/3 l/3

F F

2.2.3

Jak długi pręt o masie całkowitej m (o przekroju kołowym) można wykonać z materiału o gęstości ρ, aby pręt ten po ułożeniu go poziomo i podparciu jego końców nie uległ zniszczeniu pod własnym ciężarem. Naprężenie maksymalne na zginanie materiału pręta wynosi kg. Wskaźnik wytrzymałości przekroju porzecznego belki na zginanie dla belki o

przekroju kołowym wynosi W = πR3/4 2.2.4

Zaprojektuj belkę o przekroju prostokątnym, przy założeniu stałej jej grubości h = const, jako belkę o równomiernej wytrzymałości na rozciąganie. Obliczenia wykonaj dla obciążenia przedstawionego na rysunku. l l F B A h R_A=F/2 RB=F/2 2.2.5

Po belce o długości l podpartej na obu końcach może przemieszczać się człowiek o ciężarze G. Wyznaczyć wymaganą grubość belki o przekroju kwadratowym aby człowiek nie spowodował zniszczenia belki, jeżeli naprężenie dopuszczalne na zginanie wynosi kg

2.2.6

Wyznaczyć maksymalną wartość naprężeń rozciągających w belce suwnicy przedstawionej na rysunku, jeżeli wskaźnik wytrzymałości przekroju porzecznego belki na zginanie wynosi W. A R_A x Q B R_B Q d l

Rozwiązania: 2.1.1.R

Rozpatrzmy wydłużenie elementu pręta o długości dx znajdującego się w odległości x od dolnego końca pręta. Element ten jest rozciągany siłą równą co do wartości ciężarowi pręta znajdującego się poniżej tego elementu.

( )

x m

( )

x g Sxg

F = =ρ

Z prawa Hooke’a otrzymujemy:

( )

( )

dx E g x dx E S g x S dx E S x F dx E dx dx S x F ρ ρ = = = ∆ ⇒ ∆ = ,

Aby wyznaczyć całkowite wydłużenie pręta musimy zsumować (scałkować) wydłużenia wszystkich elementów dx. E l g dx x E g dx E g x dx l l l l 2 2 0 0 0 ρ ρ ρ = = = ∆ = ∆

∫

∫

∫

Odpowiedź: całkowite wydłużenie pręta wyniesie: 0,2mm 2 2 ≈ = ∆ E l g l ρ 2.1.2.R A)

Reakcję ściany wyznaczamy z zależności:

F R F

R− =0⇒ =

Korzystając z prawa Hooke’a otrzymujemy:

ES Fl l l l E S F E = ∆ ∆ = ⇒ =ε σ

Wydłużenie całkowite jest sumą wydłużeń obu prętów:

2 1 2 1 ES Fl ES Fl l l l=∆ +∆ =− − ∆ , gdzie 2, 1 d S =π 2 2 16 9 d S = π E d Fl l ₂ 9 25 π − = ∆ (pręt jest ściskany) B)

Reakcję ściany wyznaczamy z zależności: R+2F−F =0⇒R=−F

2 2 1 3 2 1 ) 2 ( 2 ES l F F ES Fl ES Fl l l l l=∆ +∆ +∆ = + + − ∆ ,

gdzie 2, 1 d S =π 2 2 16 9 d S = π E d Fl l ₂ 9π = ∆ C) E a Fl l ₂ 9 27 π − = ∆ E a Fl x E a Fl x B A 2 2 9 19 9 8 π π − = ∆ − = ∆ 2.1.3.R

Całkowite wydłużenie pręta składa się z wydłużenia (skrócenia) termicznego i wydłużenia mechanicznego. Z uwagi na to, że pręt jest utwierdzony jest ono zerowe.

0 = ∆ + ∆ = ∆l l_t l_m

Wydłużenie termiczne obliczamy z zależności: t

l l_t =− ∆

∆ 2α - minus oznacza oziębianie, a czynnik 2 wynika z faktu że rozpatrujemy wydłużenie obu fragmentów pręta jednocześnie.

Wydłużenie mechaniczne jest sumą wydłużeń obu fragmentów:

(

)

(

) (

)

2 1 2 1 2 1 2 1 1 1 2 1 5 7 7 4 7 d E l R P d E l R P d E l R ES l R P ES l R l l l_m π π π − = − + − = − + − = ∆ + ∆ = ∆ Z warunków zadania:

(

)

(

2

)

1 1 2 2 1 2 7 5 1 5 7 2 0 5 7 2 0 d tE P R R P d tE d E l R P tl l π α π α π α ∆ − = − = ∆ = − + ∆ − ⇒ = ∆

Drugą reakcję obliczamy z warunku równowagi sił:

(

2

)

2 1 2 2 1 2 28 5 1 7 0 7 d tE P R P R R R P R π α∆ + − = − = ⇒ = − −

(

)

2 2 2 1 1 1 5 28 5 8 5 2 7 4 d P tE d d tE P S R π α π π α

σ =− = − − ∆ = ∆ − - minus przed R1 oznacza ściskanie.

(

)

_tE d P d d tE P S R ∆ + = ∆ + = − = α π π π α σ 5 2 5 28 5 2 28 2 2 2 2 2 2 2.1.4.R 2 2 2 1 2 2 4 9 32 9 34 a Q a Q Q R a E Q t π σ π σ π α − = − = = = ∆ 2.1.5.R

Wskazówka: całkowite wydłużenie pręta wyniesie δ

Jeżeli przyjmiemy że obie reakcje skierowane są w lewo otrzymamy:

L E d P R L E d P R 6 3 2 6 3 7 2 2 2 1 δ π δ π − = + = 2.1.6.R

Rozpatrzmy element filaru o wysokości dx. Na górną powierzchnię tego elementu działa, zgodnie z warunkami

zadania siła: y dx x x q=k_c

( )

x qS

( )

x F = ,

Wypadkowa siła działająca na element dx musi być równa zeru.

(

)

( )

(

)

( )

, , 0 w dx dx w F Q x F dx x F Q F x F dx x F − + = + = + + + + r r r r

gdzie Fw oznacza siłę wyporu działającą na ten element natomiast Qdx jego ciężar.

( )

x gS x dx gS x dx qS

( ) (

x

)

gS x dx S q dx x F( + )= +ρ ( ) −ρ_w ( ) = + ρ−ρ_w ( ) Siłę działającą na dolna powierzchnię elementu możemy zapisać w postaci:

(

x dx

)

qS

(

x dx

)

(

S

( )

x dS

)

q qS

( )

x qdS

F + = + ≅ + = +

(

) ( )

( )

(

q

)

dx g x S dS dx x S g dS q w w ρ ρ ρ ρ − = − = , Po scałkowaniu otrzymamy:

( )

(

) (

)

x C q g x S ₌ ρ−ρw ₊ ln

Stałą C wyznaczamy z warunku że dla x = 0 pole S(x) = S0, stąd C = ln(S0), czyli:

( ) (

)

( )

(

)

_      − = − =       x q g S x S x q g S x S w w ρ ρ ρ ρ exp , ln 0 0

Odpowiedź: Pole przekroju filaru powinno rosnąć zgodnie z równaniem:

( )

(

)

_      − = x q g S x S _exp ρ ρw 0 2.2.1.R A)

Zadanie rozpoczynamy od wyznaczenia reakcji podporowych.

Z warunku równowagi momentów sił względem punktu A otrzymujemy:

F R R F a R a F a F M B B B A 3 2 0 6 4 0 6 3 2 2 0 = = + − = + − ⇒ =

∑

Z równowagi sił: F R F R R F A B A y 3 1 0 0 = = − + ⇒ =

∑

Następnie belkę dzielimy na trzy obszary i wyznaczamy w nich T i Mg

1. 0<x<2a F R T _A 3 1 = = Fx x R M_{g A} 3 1 = = 2. 2a<x<3a

F F F F R T _A 3 4 3 1 = + = + =

(

x a

)

Fx Fx aF Fx aF F x R M_{g A} 2 3 4 2 3 1 2 = + − = − − + = 3. 3a<x<6a F F F F F F R T _A 3 2 2 3 1 2 = + − =− − + =

(

x a

)

Fx Fa F aF Fx M_g 4 3 2 3 2 2 3 4 _{− − − =− +} =

Na podstawie obliczeń sporządzamy odpowiednie wykresy:

x M_g 6a 3a 2a 2/3Fa 2Fa x T 2a 6a 3a 4/3F -2/3F 1/3F

B) Reakcje podporowe obliczamy analogicznie jak w przypadku a) i otrzymujemy:

F R

R_A = _B=12

Podobnie jak poprzednio wyznaczamy T i Mg w trzech obszarach:

1. 0<x<a Fx x R M F R T A g A 2 1 2 1 = = = = 2. a<x<3a

(

x a

)

Fx Fx Fa Fx Fa F x R M F F R T A g A + − = + − = − − = − = − = 2 1 2 1 2 1 3. 3a<x<6a

T nie ulega zmianie na skutek działania pary sił o momencie M a więc :

F T =1 2 Fa Fx Fa Fa Fx M Fa Fx M_g 3 2 1 2 2 1 2 1 + − = + + − = + + − = Odpowiednie wykresy: x T -0,5F 0,5F 6a a x M_g 1,5Fa -0,5Fa 0,5Fa a 3a 6a C)

Reakcje podporowe wyznaczamy z równowagi momentów i sił, przy czym ciągły jednorodny rozkład siły o gęstości q traktujemy jak siłę Fq przyłożoną w jego centrum

aq R R aq R F M a R a F M M B B B q B q A = = + ⇒ = + − = + + − − ⇒ =

∑

0 2 2 0 2 0 2 0 aq aq aq R F R R F A q B A y = − = = − + ⇒ =

∑

2 0 0

Dla 3 obszarów otrzymujemy: 1. 0<x<a 2 0 2 qa M M T g = = = 2. a<x<3a qa qx qa qx qa a x q R T = _A − ⋅( − )= − + =− +2

Do wyznaczenia momentu gnącego korzystamy z faktu że wkład pochodzący od ciągłego rozkładu siły (na długości x-a) jest równoważny wkładowi od siły (równej Fq(x) = (x-a)q)

umiejscowionej w środku tego rozkładu (ramię działania tej siły to r = (x-a)/2).

(

)

( ) ( )

(

) (

)

2 2 2 2 _{q x a} a x qa qa x r x F a x R M M_g = + _A − − _q = + − − − 3. 3a<x<4a

(

)

(

)

(

)

2 3 4 2 2 3 ) 3 ( ) 3 ( 0 2 2 2 2 2 _qa qa qax qa qax qa qax qa a x R a a r x a F a x R M M T B q A g = − + + − − + = − + − − − − + = =

Wykresy sił i momentów przedstawia rysunek:

x T qa -qa a 3a 4a x M_g qa2 0,5qa2 a 3a 4a 2.2.2.R

Aby rozwiązać przedstawione zagadnienie należy zbadać rozkład naprężeń na powierzchni belki, czyli również rozkład momentu gnącego. W tym celu wyznaczmy najpierw reakcje podporowe RA i RB. Z uwagi na symetrię zagadnienia mamy:

F R F R R R R_{A B} = ⇒ = − = = 0 2 2

Następnie dzielimy belkę na trzy obszary o długości l/3 każdy i wyznaczamy w nich moment gnący: a) w obszarze I 0<x</3 Fx M_g =− b) w obszarze II l/3<x<2/3l

(

)

3 3 3 l F l R F R x l x R Fx M_{g A} = _A − − _A =−      − + − = c) w obszarze III 2/3l<x<l

(

R R F

)

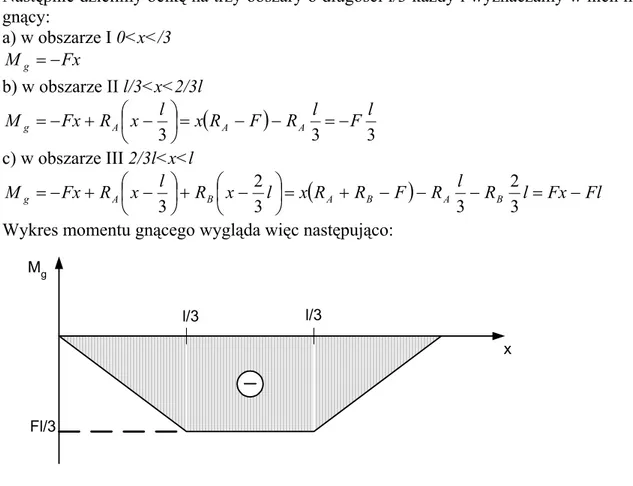
R l R l Fx Fl x l x R l x R Fx M_{g A B} = _A + _B − − _A − _B = −      − +       − + − = 3 2 3 3 2 3

Wykres momentu gnącego wygląda więc następująco:

Jak widać moment jest maksymalny (a zarazem ma stałą wartość Mg = Fa) w obszarze od l/3

do 2/3l, więc w tym obszarze należy prowadzić badania.

M_g

x

Fl/3

l/3 l/3

Aby znaleźć wartość naprężeń na powierzchni próbki korzystamy z zależności:

W M_g =

σ ,

gdzie W – wskaźnik wytrzymałości przekroju poprzecznego belki na zginanie, dla belki prostokątnej: 6 2 bh W = Po podstawieniu otrzymamy: l bh F bh Fl 2 3 6 2 2 σ σ = ⇒ =

Jeżeli za σ przyjmiemy granicę plastyczności i podstawimy otrzymamy N m m m m N F 1 10 9 2 10 9 10 / 10 2 2 2 8 2 2 8 = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ = −₋ −

Odpowiedź: Należy przyłożyć siłę l bh F 2 2 σ = =1N 2.2.3.R

Reakcje podporowe dla pręta obciążonego jednorodnie (ciężarem własnym) będą sobie równe i równe połowie ciężaru pręta:

Slg Q R R R_{A B} ρ 2 1 2 1 = = = =

Moment gnący dla tak obciążonej belki:

( )

2

(

2

)

2 1 2 1 2 1 2 1 x lx Sg Sgx Slgx x x Q x R M_g = _A ⋅ − = ρ − ρ = ρ −

Aby znaleźć maksymalną wartość momentu liczymy pochodną względem x.

(

)

2 max max 8 1 2 1 0 2 2 1 Sgl M l x x l Sg dx dM g g ρ ρ = = ⇒ = − =

Dla maksymalnego momentu gnącego korzystamy z zależności:

C g k W M = max , gdzie 4 3 R π = W C k R gl R = 3 2 2 8 4 π ρπ , ale m=ρπR2l⇒R= m ρπl 5 2 2         = g m k l C ρ ρπ

Odpowiedź: maksymalna długość pręta wynosi:

5 2 2         = g m k_C ρ ρπ l 2.2.4.R

Belka jest symetryczna, więc możemy rozpatrywać zagadnienie w przedziale 0<x<l, w tym przedziale tym moment gnący opisany jest zależnością:

Fx M_g

2 1 = ,

dla przekroju prostokątnego wskaźnik wytrzymałości wynosi:

( ) ( )

6 2 h x b x W =

( )

( )

( )

( ) ( )

6 2 h x b x M x W x W x M dop g g dop = ⇒ = _σ = σ stąd:

( )

dop h Fx x b σ 2 3 =

Czyli otrzymujemy liniowo zmieniającą się szerokość przekroju z maksimum w środku belki równym: dop h Fl b σ 2 max 3 = ,

Belka taka widziana z góry:

b(x) bma x =b (l )

Stosowanie takiej belki byłoby jednak kłopotliwe, dlatego w praktyce stosuje się belki o innym kształcie. jeżeli podzielimy (myślowo) naszą belkę na paski tak jak pokazują linie przerywane i odpowiednio złożymy, to otrzymamy belkę będącą w istocie piórem resoru:

F

2.2.5.R

Wyznaczmy reakcję podporową w podporze A, w tym celu skorzystamy z warunku

x

G

B A

zerowania się momentów względem podpory B:

( )

(

)

( )

(

)

l x l G x R x l G l x R M A A B − = = − + − =

∑

0

Moment gnący na lewo od człowieka:

( )

( )

(

)

l x l G x R

M_g ξ = _A ⋅ξ = ξ − , gdzie ξ jest odległością od lewej podpory.

Moment ten osiąga wartość ekstremalną w punkcie działania siły G (jest to zarazem wartość maksymalna dla całej belki z uwagi na brak innych sił poza reakcjami podporowymi)

( )

l Gx Gx x M_g 2 − =

Zbadajmy w jakim położeniu (x) człowiek wywoła największy moment gnący, w tym celu policzmy pochodną:

( )

l x l Gx G dx x dM_g 2 1 0 2 0 = = − ⇒ =

Czyli maksymalny moment gnący dla: x l 2 1 = Pl M_g 4 1 max =

Z warunku wytrzymałości na zginanie:

W M k_g = gmax , gdzie 3 6 1 h = W 3 2 3 h Pl k_g = ostatecznie: 3 2 3 g k Pl h= .

Odpowiedź: belka musi mieć grubość co najmniej równą: 3 2 3 g k Pl h=

2.2.6.R

Z warunków równowagi momentów otrzymujemy reakcje podporowe:

(

)

(

x d

)

l Q R d x l l Q R B A + = − − = 2 2 2

Momenty gnące w miejscach przyłożenia sił (tylko tam mogą one osiągać maksimum):

(

l x d

l Qx x R

M_g1 = _A = 2 −2 −

)

, dla siły na lewej osi wózka

(

x d

)(

l x d

)

Qd l Q Qd d x R

M_g2 = _A( + )− = + 2 −2 − − , dla siły na prawej osi wózka W celu znalezienia maksymalnych wartości momentów gnących liczymy ich pochodne względem x i przyrównujemy je do zera.

2 max 1 1 1 2 2 4 2 0       − = − = ⇒ = d l l Q M d l x dx dM g g 2 max 2 2 2 2 2 4 3 2 0       − = − = ⇒ = d l l Q M d l x dx dM g g

Jak widać oba momenty mają taką samą wartość maksimum, a więc do policzenia maksymalnego naprężenia możemy wziąć którykolwiek z nich.

2 max max 2 2      − = = l d lW Q W M_g σ

Maksymalna wartość naprężeń rozciągających wyniesie: 2 max 2 2      − = l d lW Q σ