Badania polimorfizmu i dynamiki
izomerów neoheksanolu
Ewa Juszyńska
Praca na stopień doktora nauk fizycznych wykonana pod kierunkiem
Prof. dr hab. Marii Massalskiej - Arodź
Instytut Fizyki Jądrowej im. H. Niewodniczańskiego Polskiej Akademii Nauk
Zakład Badań Strukturalnych
Serdecznie pragnę podziękować mojemu promotorowi Prof. dr hab. Marii
Massalskiej-Arodź za cenne rady i poświęcony czas, podzielenie się wiedzą,
ważne wskazówki i korekty, które umożliwiły mi napisanie niniejszej rozprawy.
Dziękuję za wprowadzenie mnie do świata nauki.
Dziękuję Pracownikom Zakładu Badań Strukturalnych za stworzenie miłej
atmosfery. Szczególnie pragnę podziękować Dr. Piotrowi M. Zielińskiemu i Mgr
inż. Jackowi Ściesińskiemu za nieocenioną pomoc w przeprowadzeniu pomiarów
metodą kalorymetrii adiabatycznej.
Dziękuję Prof. dr hab. Antoniemu Kocotowi z Instytutu Fizyki
Uniwersytetu Śląskiego za pomoc w przeprowadzeniu badań metodą
spektroskopii dielektrycznej.
Dziękuję Dr Ireneuszowi Natkańcowi oraz Prof. dr hab. Krystynie
Hołdernej –Natkaniec z Instytutu Fizyki Uniwersytetu im. Adama Mickiewicza w
Poznaniu za naukę i pomoc w pomiarach neutronowych oraz przy interpretacji
wyników metodami chemii kwantowej. Bardzo jestem wdzięczna za przekazaną
wiedzę i za poświęcony czas podczas mojego stażu w Zjednoczonym Instytucie
Badań Jądrowych w Dubnej.
Dziękuję mojej Rodzinie szczególnie Mężowi za okazane wsparcie i cierpliwość.
Ewa
Juszyńska
Praca ta powstała częściowo ze środków projektu badawczo promotorskiego
nr. NN 202 176 135 finansowanego przez Komitet Badań Naukowych
Spis treści
I. Wstęp………...………...4
II. Analiza termiczna przejść fazowych………...……….…12
II.1. Różnicowa kalorymetria skaningowa (DSC)…………..………..12
II. 1. 1. Literaturowe rezultaty badań przejść fazowych w 2,2-dwumetylobutanolu i 3,3-dwumetylobutanolu……….……….….14
II. 1. 2. Rezultaty badań przejść fazowych w czterech izomerach neoheksanolu metodą DSC………..…………...……..15
II. 2. Kalorymetria adiabatyczna………...….…...22
II. 2. 1. Budowa kalorymetru adiabatycznego………..……..………..25
II. 2.2. Obliczenia funkcji termodynamicznych……….…...…………28
II. 2.3. Pomiary kalorymetryczne dla trzech izomerów neoheksanolu…...…..………31
III. Spektroskopia dielektryczna………..……….……43
III.1. Układ pomiarowy stosowany w pomiarach dielektrycznych………...…45
III.2. Analiza sytuacji fazowej oraz opis zjawiska relaksacji dielektrycznej dla wybranych dwumetylobutanoli………...……46
IV. Dynamika wibracyjna dwumetylobutanoli………...……64
IV.1. Spektroskopia absorpcyjna………..…...….67
IV.1.1. Aparatura pomiarowa………...……...68
IV.1.2. Badanie dynamiki izomerów neoheksanolu………..…...……70
IV.1.2.1. Badania w zakresie dalekiej podczerwieni………..…………..71
IV.1.2.2. Badania w zakresie środkowej podczerwieni………..…...……...78
IV. 2. Spektroskopia neutronowa………...………...82
IV.2.1. Własności i źródła neutronów ………..…………82
IV.2.2. Podział spektroskopowych metod neutronowych ……….…...84
IV. 2.3. Rozpraszanie neutronów. ……….……...…85
IV.2.3.1 Nieelastyczne rozpraszanie neutronów………...…....90
IV.2.3.2 Dyfrakcja neutronów (NPD)………...…..…..91
IV.2.4. Spektrometr odwrotnej geometrii NERA-PR….………..………93
IV.2.5. Eksperymentalne wyniki IINS ……….…………97
IV.2.6. Eksperymentalne wyniki NPD……….…..………….106
IV. 3. Modelowanie struktury i dynamiki wibracyjnej molekuł dwumetylobutanoli metodami mechaniki kwantowej………..………..….…………110
IV.3.1 Optymalizacja struktury molekuły………..……....….………111
IV.3.2 Klastry (dimery, trimery, tetrametry)…...115
IV.3.3. Obliczenia częstotliwości wibracyjnych ……….….….……….118
a) izolowana molekuła……….….…..….……118
b) dimery, trimery oraz tetrametry………....…………..124
IV.4. Podsumowanie wyników badań spektroskopowych………...…………126
V. Podsumowanie………..……….127
Spis literatury……….…………...………...………...………129 Dodatek 1……….D1 Dodatek 2……….D9 Dodatek 3………..….D22
I. WSTĘP
Tematem rozprawy doktorskiej są badania polimorfizmu faz stałych i właściwości dynamicznych molekuł izomerów dwumetylobutanoli. Przedmiotem badań były cztery dwumetylobutanole (DM-B) o sumarycznym wzorze molekuł C6H13OH, a mianowicie
2,2-dwumetylo-1-butanol (2,2-DM-1-B) czyli CH3CH2C(CH3)2CH2OH zwany neoheksanolem,
3,3-dwumetylo-1-butanol (3,3-DM-1-B) czyli (CH3)3CCH2CH2OH, 3,3-dwumetylo-2-butanol
(3,3-DM-2-B) czyli (CH3)3CCH(OH)CH3 oraz 2,3-dwumetylo-2-butanol (2,3-DM-2-B) czyli
(CH3)2CHC(CH3)2OH. Molekuły poszczególnych DM-B różnią się między sobą obecnością
oraz położeniem grup funkcyjnych CH3, CH2, CH oraz OH (rys. 1-4). W molekułach
badanych substancji grupa hydroksylowa jest podstawiona w alifatycznym butanie odpowiednio do atomu węgla oznaczonego jako C(1) (1-butanol) lub jako C(2) (2-butanol), co powoduje różny polimorfizm i wpływa na dynamikę molekularną faz stałych [Massalska- Arodź i inni, 2004; Juszyńska i inni, 2006 a, b]. Molekuły 1-butanolowe posiadają grupy metylenowe CH2, w przeciwieństwie do 2-butanolowych, które posiadają grupy C-H. Ze
względu na budowę molekuł izomery 2,2-DM-1-B i 3,3-DM-1-B są alkoholami pierwszorzędowymi, 3,3-DM-2-B – jest alkoholem drugorzędowym, zaś 2,3-DM-2-B – trzeciorzędowym. Molekuły DM-B należą do grupy symetrii „C1” co oznacza, że nie można określić ich osi, płaszczyzn i środka symetrii. Istnieje jedynie tożsamościowy element symetrii E, który „działa” poprzez obrót o 360o wokół dowolnie wybranej osi, co jest równoznaczne z pozostawieniem molekuły bez żadnej zmiany.
(a) (b)
Rysunek 1. Schemat molekuły 2,2-DM-1-B typu trans (a) i gauche (b). Zaznaczone są atomy kolejnych węgli oraz atom tlenu.
(a) (b)
Rysunek 2. Schemat molekuły 3,3-DM-1-B typu trans (a) i gauche (b). Zaznaczone są atomy kolejnych węgli oraz atom tlenu.
Rysunek 3. Schemat molekuły 3,3-DM-2-B. Zaznaczone są atomy kolejnych węgli oraz atom tlenu.
(a) (b)
Rysunek 4. Schemat molekuły 2,3-DM-2-B typu trans (a) i gauche (b). Zaznaczone są atomy kolejnych węgli oraz atom tlenu.
Na rysunkach 1-4 naniesione są wektory momentów dipolowych (czerwone strzałki) głównych grup funkcyjnych tworzących molekuły badanych związków. Momenty dipoloweμr poszczególnych wiązań wynoszą odpowiednio 1.5 D dla O-H, 1.2 D dla C-O,
oraz 0,3 D zarówno dla C-H jak i dla grupy funkcyjnej CH3, (1 D = 3,33564 10–30 C m)
[Debye, 1929]. Zwroty wektorów momentów dipolowych określone są od atomu posiadającego cząstkowy ładunek dodatni do atomu posiadającego cząstkowy nadmiar elektronów. Moment dipolowy μr polarnych cząsteczek złożonych, jakimi są molekuły badanych związków jest sumą momentów dipolowych poszczególnych wiązań. Prezentowane schematy molekuł DM-B zostały otrzymane z obliczeń kwantowo mechanicznych metodą DFT. Wartości kątów zawartych pomiędzy wiązaniami i długości poszczególnych wiązań, które posłużyły do wyznaczenia momentów dipolowych μr molekuł omawianych związków zawarte są w Tabeli IV.3 w rozdziale IV.3.
Dzięki rozgałęzionej strukturze wiązań C-C wszystkie molekuły DM-B są, z dobrym przybliżeniem, globularne. Taka geometria molekuł determinuje pojawienie się w tych substancjach, oprócz faz uporządkowanego kryształu [White i Geballe, 1979], również faz plastycznych typu ODIC zwanych też fazami rotacyjnymi ze względu na swobodę zmian reorientacyjnych molekuł [Suga, 2003]. Własności kryształów plastycznych odkryte zostały przez Timmermansa [Timmermans, 1961]. Zarówno fazy krystaliczne jak i fazy plastyczno-krystaliczne charakteryzują się uporządkowaniem dalekiego zasięgu środków ciężkości molekuł rozłożonych w sieci krystalicznej. W trakcie ogrzewania uporządkowanego kryształu w procesie topnienia następuje jednoczesne uruchomienie translacyjnych i rotacyjnych stopni swobody. Natomiast przy topnieniu fazy plastycznej uruchamiane zostają jedynie translacyjne stopnie swobody. Uruchomienie rotacyjnych stopni swobody następuje w niższej temperaturze przy przejściu z fazy krystalicznej do fazy plastycznego kryształu. Dla organicznych substancji o złożonych molekułach pomiędzy uporządkowanym kryształem a nieuporządkowaną cieczą może pojawić się kilka faz pośrednich, w których dynamika dotyczy różnych stopni swobody [Kitajgorodski, 1976].
Na rysunku 5 przedstawiony został schematyczny podział faz termodynamicznych przewidywanych dla izomerów DM-B o globularnym kształcie molekuł. Zarówno dla przechłodzonej cieczy izotropowej jak również dla faz rotacyjnych można oczekiwać tworzenia fazy szklistej. Stan krystaliczny i szklisty są odmiennymi formami stanu stałego materii [Allen, 1994]. Istnieje kilka definicji szkła cieczy, które opisują ich własności fizyczne - np. „szkło wykazuje izotropię wszystkich własności fizycznych”, czy definicja morfologiczna - „szkło jest amorficzne, czyli nie posiada wykształconej postaci, przyjmuje zaś kształt naczynia, w którym zastygło”. Uważa się, że „strukturę szkła charakteryzuje brak uporządkowania dalekiego zasięgu, a w konsekwencji brak refleksów na dyfraktogramach
rentgenowskich” oraz że szkło powstaje podczas ochładzania fazy ciekłej, w temperaturze zwanej temperaturą witryfikacji, gdy lepkość fazy ciekłej osiąga 1013 P·s [Novikov i Sokolov, 2004].
Rysunek 5. Schemat przewidywanych faz termodynamicznych w układach o globularnych molekułach DM-B.
W ostatnich dziesięcioleciach materiały tworzące szkła są intensywnie badane [Angell, 1995]. Począwszy od jednej z pierwszych definicji zaproponowanej przez Kauzmanna [Kauzmann, 1948], która mówi, że szkło to ciecz o zamrożonych pewnych stopniach swobody pojecie szkła ulegało znacznemu rozszerzeniu. W połowie ubiegłego wieku ok. 1968 roku, rozpoczęły się badania innej odmiany szkieł. Są to tzw. szkła orientacyjne czyli szkła faz rotacyjnych [Adachi i inni, 1968], charakteryzujące się zamrożonym nieporządkiem orientacyjnym molekuł, któremu towarzyszy ich regularne rozłożenie w sieci krystalicznej. W latach siedemdziesiątych ubiegłego stulecia zostały rozpoczęte badania tzw. szkieł anizotropowych [Suga i Seki, 1974], gdzie środki ciężkości molekuł zamrożonej fazy ciekłokrystalicznej są przypadkowo rozmieszczone w przestrzeni próbki, podczas gdy daleko- zasięgowy charakter wykazuje uporządkowanie długich osi molekuł. Obecnie prowadzone są również badania szkieł, w których nieporządek odnosi się do konformacji łańcuchów molekularnych w fazie krystalicznej [Saito i Wright, 1983].
Szkło fazy ciekłej otrzymujemy przy dostateczne szybkim ochładzaniu, gdy uda się uniknąć wcześniejszej krystalizacji. Natomiast szkło fazy plastycznej uzyskujemy w procesie ochładzania, gdy najpierw nastąpi krystalizacja fazy plastycznej, a dalsze ochładzanie nie wywoła przejścia do fazy uporządkowanego kryształu. Temperatura Tg przejścia szklistego
podczas ochładzania przechłodzonej cieczy szacowana jest jako Tg ≈ 2 Tm/3, gdzie Tm jest
temperaturą topnienia [Sakka i inni, 1986 i 1986; Stickel i inni, 1996]. Z obniżaniem temperatury lepkość przechłodzonej fazy ciekłej silnie rośnie, czemu towarzyszy coraz powolniejszy ruch molekuł. W temperaturze witryfikacji (zeszklenia) ruchy molekuł są tak wolne, że zmiany konfiguracji molekuł nie są w stanie nadążyć za zmianami temperatury i substancja przestaje być w równowadze termodynamicznej. Pomiędzy temperaturami Tm i Tg
czasy charakterystyczne τ ruchów molekuł ulegają zmianie o szesnaście rzędów wielkości, przy czym przyjmuje się, że w temperaturze Tg wartość τ wynosi 100 s [Donth, 2001].
Gwałtowne spowolnienie dynamiki molekuł w trakcie obniżania temperatury do Tg
wywołuje „superarrheniusowską” relaksację strukturalną (tzw. proces α). Zależność czasu relaksacji od temperatury jest opisywana równaniem Vogela - Fulchera – Tammanna [Vogel, 1921; Grest i Cohen, 1980; Scherer, 1992]
) /( ( exp ) (T =τ0 DT0 T −T0 τ , (I.1)
gdzie τ0 to czas relaksacji w granicy wysokich temperatur, parametr D opisuje odchylenie od
liniowego „arrheniusowskiego” przebiegu zależności temperatury lg τ (1/Τ); T0, przy której
zamiera ruch molekuł, jest temperaturą o kilkadziesiąt stopni (30 - 50 K) niższą od Tg
odpowiadającą tzw. temperaturze Kauzmanna Tk [Stickel i inni, 1996; Kokshenev, 1999;
Alba-Simionesco i inni, 1999]. Parametr m~1/D ma istotny sens fizyczny [Novikov, 2005] i służy do klasyfikacji szkieł. Dla dużych wartości m (tzw. „fragility”), uzyskuje się kruche szkła (silne odstępstwo od zachowania arrheniusowskiego), podczas gdy dla małych wartości parametru m uzyskujemy silne szkła (zachowanie arrheniusowskie). Duże wartości parametru m≈ 200 zostały stwierdzone dla polimerów. Dużo mniejsze wartości parametru m stwierdzono dla alkoholi o różnej budowie molekularnej, takich jak alkohole cykliczne [Dissado i Hill, 1983], gliceryna [Böhmer i inni, 1993], salol [Stickel i inni, 1996], metanol [Natkaniec i inni, 2005], etanol [Suga i inni, 1974], neoheksanol [Johari, 1976] itp. Opis dynamiki w szkłach oraz w przechłodzonych fazach, z których one powstają jest trudny ze względu na niearheniusowski, a także niedebajowski charakter procesu relaksacji strukturalnej. Spowolnienie dynamiki molekuł przy zmierzaniu do przejścia szklistego jest związane ze wzrostem kooperacyjności ruchów molekuł, czemu towarzyszy wzrost energii
aktywacji [Adam i Gibbs, 1965]. Miarą wielkości kooperacyjności jest parametr 1-b zdefiniowany przez funkcję odpowiedzi układu Kolhrauscha - Williamsa – Wattsa [Williams i Watts, 1970; Palmer i inni, 1984] w postaci
b T F
t
F( )= (0) exp (−(τ/τ( )) ). (I.2) Opisuje ona relaksacyjne dochodzenie do równowagi w niskich temperaturach, odmiennie od eksponencjalnego F(t) w wysokich temperaturach. Parametr b przyjmuje wartości 0≤b≤1.
Dla niektórych substancji szkłotwórczych oprócz relaksacji strukturalnej można zaobserwować kilka innych procesów takich jak szybka bądź wolna relaksacja typu β [Buchenau i inni 1986; Johari i Goldstein, 1970 i 1971], bardzo wolne mody Fischera [Donth, 2001] oraz tzw. pik bozonowy związany z drganiami wibracyjnymi molekuł w okolicy Tg [Buchenau i inni 1986; Donth, 2001].
W ujęciu termodynamicznym przejście pomiędzy przechłodzoną cieczą a szkłem nie jest przejściem fazowym ani pierwszego ani drugiego rodzaju gdyż decyduje o nim kinetyka ruchów molekularnych [Patkowski, 2001]. Klasyfikowane jest, jako słabe przejście fazowe drugiego rodzaju gdyż wykazuje pewne charakterystyczne dla tego typu przemian własności [Allen i Zinkernagel 1994]. Przemiany zachodzące w fazach szklistych są nierównowagowe, przy czym fazy szkliste są fazami metastabilnymi [Sastry, 2001] o bardzo długim czasie życia. Objawia się to relaksacją entalpii opisywaną również równaniem 2.
Dotychczas fazę szklistą stwierdzono w dwóch izomerach DM-B. Dla 2,2-DM-1-B badania przeprowadzone były metodą DTA [Chan i Johari, 1974; Edelmann, 1990, Edelmann i inni 1991] oraz relaksacji dielektrycznej [Johari, 1976], również przy podwyższonym ciśnieniu [Edelmann, 1990]. Dla 3,3-DM-1-B badania przeprowadzone były metodą DSC, kalorymetrii adiabatycznej oraz relaksacji dielektrycznej [Massalska-Arodź i inni, 2004].
W celu pełnej identyfikacji faz stałych występujących w dwumetylobutanolach oraz określenia dynamiki ich molekuł przeprowadzone zostały badania czterech izomerów kilkoma komplementarnymi metodami eksperymentalnymi. Badania polimorfizmu czterech substancji DM-B przeprowadzone zostały przy użyciu dwóch metod kalorymetrycznych oraz spektroskopii optycznej w zakresie dalekiej i środkowej podczerwieni w Zakładzie Badań Strukturalnych, Instytutu Fizyki Jądrowej PAN w Krakowie. Określenie wewnętrznej dynamiki molekuł DM-B przy pomocy metody neutronowej, tzw. nieelastycznego niekoherentnego rozpraszania neutronów IINS, jak również pomiary dyfrakcji neutronowej NPD przeprowadzono w Zjednoczonym Instytucie Badań Jądrowych w Dubnej. Badania dielektryczne zostały wykonane w Zakładzie Biofizyki i Fizyki Molekularnej, Uniwersytetu
Śląskiego. Obliczenia kwantowo-mechaniczne metodą funkcjonału gęstości DFT oraz pół-empiryczną metodą PM3 zostały przeprowadzone w Poznańskim Centrum Superkomputerowo-Sieciowym PCSC, natomiast obliczenia metodą Hartree-Focka (HF) przeprowadzono w Akademickim Centrum Komputerowym CYFRONET AGH.
Praca została podzielona na pięć rozdziałów.
WSTĘP - jest wprowadzeniem do poznania materiału badawczego, zastosowanych metod eksperymentalnych oraz określa cel prowadzonych badań. Przedstawiono również przewidywane fazy termodynamiczne, których obecność jest silnie zdeterminowana geometrycznym kształtem molekuł dwumetylobutanoli.
Rozdział drugi poświęcony jest zaprezentowaniu wyników badań eksperymentalnych mających na celu określenie polimorfizmu faz stałych dwumetylobutanoli. Rozdział ten zawiera wyniki badań kalorymetrycznych z zastosowaniem metody różnicowej kalorymetrii skaningowej DSC oraz metody kalorymetrii adiabatycznej. Przedstawię wartości funkcji termodynamicznych dla przejść fazowych uzyskanych dzięki pomiarom zależności ciepła właściwego od temperatury. Na podstawie analizy zgromadzonych wyników o sytuacji fazowej dwumetylobutanoli zostaną zaproponowane diagramy fazowe.
Rozdział trzeci dotyczy określenia dynamiki molekuł dwumetylobutanoli metodą spektroskopii dielektrycznej.
W kolejnym rozdziale czwartym zostaną przedstawione wyniki badań prowadzonych metodą spektroskopii absorpcyjnej (IR) i niekoherentnego nieelastycznego rozpraszania neutronów (IINS). W celu interpretacji wibracyjnych widm IINS oraz IR przeprowadzono optymalizację struktury zarówno w przybliżeniu izolowanej molekuły jak i dla klastrów dimerów lub trimerów bądź tetrametrów molekuł połączonych oddziaływaniami typu wiązania wodorowego. Metodami chemii kwantowej: pół - empiryczną PM3 i funkcjonału gęstości DFT (metoda B3LYP z bazą 6-311G**) oraz HF za pomocą programu Gaussian 03, wyliczono częstości i intensywności pasm drgań normalnych w widmach IINS i IR dla izolowanych molekuł. Dla klastrów zbudowanych z dwóch, trzech lub czterech molekuł wyliczone zostały charakterystyczne pasma typowe dla układów z wiązaniem wodorowym. Charakter wibracji drgań normalnych w widmach został określony na podstawie wizualizacji drgań za pośrednictwem programu gOpenMol. Wyniki obliczeń kwantowo-mechanicznych zostaną również zawarte w Dodatkach 1 oraz 2, dotyczących dynamiki wibracyjnej
W rozdziale piątym przedstawione zostanie podsumowanie uzyskanych informacji na temat własności termodynamicznych i dynamicznych czterech dwumetylobutanoli.
Praca zawiera również spis używanych symboli fizycznych oraz spis literatury, z której korzystano przy jej przygotowywaniu, a także publikacji o znaczeniu historycznym dla rozpatrywanych zagadnień.
Uzupełnieniem niniejszej rozprawy doktorskiej są Dodatki 1-3.
Dodatek 1 dotyczy teoretycznych podstaw obliczeń metodami chemii kwantowej.
Dodatek 2 zawiera tabele z zestawieniem częstotliwości eksperymentalnych G(ν) oraz IR wraz z wyliczonymi metodą DFT, PM3 i HF oraz przypisanie rodzaju drgania dla izolowanych molekuł czterech dwumetylobutanoli.
W dodatku 3 dołączone zostały tabele z wynikami ciepła właściwego uzyskane metodą kalorymetrii adiabatycznej, które posłużyły do określenia odpowiednich funkcji termodynamicznych, o których mowa jest w rozdziale drugim.
II. Analiza termiczna przejść fazowych
Terminem analizy termicznej określa się zespół metod laboratoryjnych, przeznaczonych do badań własności fizycznych substancji pod wpływem zmian temperatury. Twórcą tej metody jest Le Chatelier, który jako pierwszy opisał badania wielu reakcji w ciele stałym na skutek zmian temperatury [Shelby, 2005]. Za pośrednictwem analizy termicznej można między innymi identyfikować skład fazowy substancji, pozwala ona dokonywać pomiarów entalpii oraz entropii jak również badać kinetykę i mechanizmy szeregu reakcji. Przy odpowiedniej czułości układu pomiarowego na zmiany temperatury, jest ona stosowana w zakresie analityki chemicznej, kinetyki procesów krystalizacji oraz przemian fazowych. Pozwala również określić stabilność termodynamiczną faz oraz służy do badań reaktywności cieczy i ciał stałych. Znanych jest wiele metod analizy termicznej, które dzieli się w zależności od mierzonych dzięki nim wielkości [Schulze 1974; Shelby, 2005].
II.1. Różnicowa kalorymetria skaningowa (DSC)
Do występnego określenia polimorfizmu dwumetylobutanoli, jak również do wyznaczenia wartości funkcji temodynamicznych (entalpii i entropii) została wykorzystana różnicowa kalorymetria skaningowa (DSC – Differential Scanning Calorymetry). Wyniki tej metody rejestrowane są w postaci zmian przepływu ciepła w jednostce czasu w zależności od temperatury.
Badania zostały przeprowadzone za pomocą mikrokalorymetru DSC 7 firmy Perkin – Elmer w Zakładzie Badań Strukturalnych IFJ PAN. Schemat mikrokalorymetru przedstawiony jest na rysunku II.1. Posiada on komputerowy układ sterowania zmianami temperatury oraz urządzenie rejestrujące efekty cieplne. Masa badanych próbek umieszczonych w aluminiowych naczyńkach zawierała się w przedziale od ok. 5 do 11 mg. Ogólnie zasadę metody DSC można przedstawić następująco: zarówno próbkę badaną jak i próbkę wzorcową, dla której w analizowanym przedziale temperatur nie zachodzą żadne przemiany fazowe, ogrzewa się z jednakową szybkością (ΔT/Δt = const) i mierzona jest różnica mocy dostarczonej do obu naczyniek (próbki i wzorca) w funkcji temperatury. Innymi słowy, dokonujemy pomiaru różnicy przepływu ciepła ΔQ/Δt pomiędzy oboma naczyńkami, w funkcji temperatury. Wielkość różnicy entalpii ΔH próbki w funkcji temperatury jest proporcjonalna do pojemności cieplnej próbki, jeżeli naczyńko z badaną próbką oraz wzorcowe naczyńko mają takie same charakterystyki termiczne.
Rysunek II.1. Schemat mikrokalorymetru DSC 7 firmy Perkin – Elmer.
Natomiast w okolicy przejścia fazowego aby utrzymać warunek stałego tempa zmian temperatury porcje ciepła dostarczane do próbki w naczyńku i do wzorcowego naczyńka są już inne. Jest to przyczyną, że rejestruje się anomalie na krzywej
t Q Δ Δ
. Miarą wielkości efektu cieplnego ΔH obserwowanego przy przejściu fazowym dla ustalonej masy próbki jest powierzchnia pod anomalią
T T t t Q H T T Δ Δ Δ Δ Δ = Δ
∫
2 1 , (II.1)gdzie T1 oznacza temperaturę rozpoczęcia zaś T2 temperaturę zakończenia przemiany fazowej
[Janik, 1989].
Próbki badanych dwumetylobutanoli były ochładzane i ogrzewane w zakresie temperatur od temperatury pokojowej T = 298 K do temperatury T = 93 K, z różnym tempem ΔT/Δt zmian temperatury, które zmieniano w zakresie od 1 K/min do 25 K/min. Temperatura była mierzona za pomocą czujników platynowych umieszczonych pod dnem naczyniek pomiarowych. Przyjęto, że temperatura przejścia fazowego jest wartością temperatury w maksymalnym punkcie piku. Błąd pomiaru temperatury wynosi 0.5 K. Przed rozpoczęciem pomiaru przeprowadzono kalibrację aparatury przy pomocy indu, cynku oraz wody o znanych wartościach temperatury przemian fazowych oraz dokonano pomiaru tzw. linii bazowej, która powinna być równoległa do osi temperatury. Rejestrowane termogramy są różnicą efektów termicznych i linii bazowej. We wszystkich dynamicznych metodach pomiarowych takich jak DSC obserwuje się tzw. histerezę aparaturową dodatnią lub ujemną. Jest to zjawisko związane z nieznacznym wyprzedzeniem (przy ochładzaniu) lub opóźnieniem (przy
ogrzewaniu) wskazań termometru w stosunku do rzeczywistej temperatury badanej próbki. Daje to błąd rzędu 0.5 K przy oszacowaniu temperatury przejścia fazowego.
II. 1. 1. Literaturowe rezultaty badań przejść fazowych
w 2,2-dwumetylobutanolu i 3,3-dwumetylobutanolu
Dwa spośród czterech izomerów neoheksanolu czyli 2,2-DM-1-B oraz 3,3-DM-1-B, zostały wcześniej zbadane przy zastosowaniu metody termicznej analizy różnicowej DTA [Chan i Johari, 1974; Edelmann, 1990, i inni 1991] i DSC [Massalska–Arodź i inni, 2004]. Temperatury przejść fazowych dla neoheksanolu podane przez R. K. Chan’a i G. P. Johari’ego [Chan i Johari, 1974] z pomiarów DTA są następujące: Tg = 163 K Tc = 183 K,
oraz Tm = 241 K, gdzie: Tg, Tc i Tm to temperatury odpowiednio przejścia szklistego,
krystalizacji i topnienia. Uzyskana faza szklista jest szkłem fazy plastycznej. Wyniki badań prowadzonych przez R. K. Chan’a i G. P. Johari’ego również dla innych neo-alkoholi ukazują, że substancje te, podobnie jak alkohole alifatyczne, które były przedmiotem badań Timmermansa [Timmermans, 1961], charakteryzują się posiadaniem fazy plastycznej. Obie klasy substancji są glass-formerami i tworzą fazę szklistą plastycznych kryształów.
Substancja 2,2DM-1-B była przebadana przez R. Edelmanna, przy użyciu metody DTA przy różnych ciśnieniach p w zakresie temperatur 100 K - 340 K [Edelmann, 1990; Edelmann i inni 1991]. Dla neoheksanolu przy p=0 uzyskane zostały przejścia fazowe w następujących temperaturach: C3’→C2 (187.9 K), C3’’→C2 (196.4 K), C3→C2 (198.6 K), C2→C1 (210.4 K), C1→L (250.6 K) oraz uzyskano przejście szkliste. Szkło uległo mięknięciu przy temperaturze 158 K. Przy wyższych ciśnieniach polimorfizm staje się jeszcze bogatszy o dodatkową fazę CIV (rys.II.2).
Substancja 3,3-DM-1-B została przebadana metodą DSC na mikrokalorymetrze Pyris-1 DSC firmy Perkin - Elmer w Osace, Japonia. Zarejestrowany polimorfizm [Massalska– Arodź i inni, 2004] silnie zależy od szybkości ochładzania substancji, mianowicie wolne ochładzanie z tempem 5 K/min powoduje rejestrację anomalii na krzywej ochładzania, która odpowiada za spontaniczną krystalizację przechłodzonej cieczy izotropowej w temperaturze T = 195 K. Natomiast, ochładzanie badanej próbki z tempem 10 K/min nie pozwoliło na zaobserwowanie żadnej anomalii na krzywej termicznej. Jednakże w trakcie ogrzewania uzyskano przejście szkliste w temperaturze około Tg = 150 K, które na termogramie objawiło
Rysunek II.2. Diagram fazowy 2,2-DM-1-B [Edelmann, 1990]. Litera S jest skrótem od solid. W pracy, w opisie wyników jest zastąpiona literą C.
się poprzez niewielki wzrost przepływu ciepła w jednostce czasu. Niskotemperaturowa faza jest tzw. fazą szklistą cieczy o zamrożonym nieporządku pozycyjnym i orientacyjnym molekuł. W trakcie dalszego ogrzewanie próbki zaobserwowano tzw. zimną krystalizację (nazywaną tak dla odróżnienia do krystalizacji uzyskiwanej przy ochładzaniu) w temperaturze Tcc = 188 K. Zarejestrowana krystalizacja odpowiada przejściu fazowemu pomiędzy
przechłodzoną cieczą izotropową, do której nastąpiło mięknięcie fazy szklistej, a fazą krystaliczną o uporządkowaniu pozycyjnym i orientacyjnym molekuł. Duża wartość entalpii obserwowana dla wyżej temperaturowej anomalii zarejestrowanej przy 231 K odpowiada za topnienie stabilnej fazy krystalicznej.
II. 1. 2. Rezultaty badań przejść fazowych
w czterech izomerach neoheksanolu metodą DSC
Celem prowadzonych badań własności cieplnych czterech dwumetylobutanoli za pomocą metody DSC było wyznaczanie temperatur przejść fazowych, ich rodzaju oraz oszacowanie efektów termicznych jakie im towarzyszą. Przeprowadzone pomiary dały informacje o podstawowych własnościach termicznych badanych alkoholi.
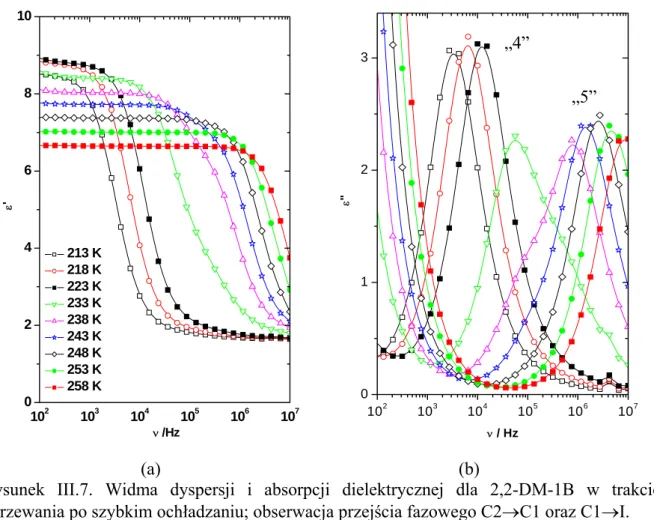
Uzyskane termogramy DSC (Rys. II.3-II.6) przedstawiają przepływ ciepła w zależności od temperatury. Z pomiarów DSC przeprowadzonych dla 2,2-DM-1-B wynika, że podczas ochładzania próbki z szybkością 10 K/min uzyskano egzotermiczną przemianę
160 180 200 220 240 260 0 20 40 60 80 100 Δ W [m W] Temperatura [K] 10 K/min 160 180 200 220 240 260 280 300 -5 0 5 10 15 20 25 Δ W [m W] Temperatura [K] 10 K/min (a) (b)
Rysunek II.3. Termogram DSC otrzymany podczas ochładzania (niebieska krzywa) i ogrzewania (czerwona krzywa) 2,2-dwumetylo-1-butanolu (a) oraz zarejestrowany przy ogrzewaniu z szybkością 10 K/min po raptownym schłodzeniu próbki do temperatury 150 K (b) [Juszyńska i inni, 2006].
świadczącą o krystalizacji cieczy w temperaturze Tc = 212 K, czyli o pojawieniu się
uporządkowania pozycyjnego molekuł neoheksanolu. Dalsze ochładzanie substancji nie spowodowało innych przemian fazowych. Natomiast podczas ogrzewania neoheksanolu z tą samą szybkością zmian temperatury uzyskano dwie endotermiczne anomalie w temperaturze 235.5 K i 250.8 K. Niskotemperaturowa przemiana odpowiada za przejście z fazy stałej do innej fazy stałej o większym nieporządku molekuł. Anomalia obserwowana w temperaturze 250.8 K odpowiada za topnienie fazy stałej do fazy izotropowej cieczy. Takie zachowanie próbki obrazuje przedstawiony rejestrogram na rys. II.3a. Z kolei podczas ogrzewania tej próbki, po wcześniejszym bardzo szybkim jej ochładzaniu do temperatury ok. 150 K, uzyskano dwie anomalie w temperaturach 178.7 K i 234,7 K (rys. II.3b). Niskotemperaturowa
endotermiczna przemiana wydaje się być przemianą do fazy metastabilnej, gdyż powtarzając pomiary w podobnych warunkach nie udało się zaobserwować jej ponownie. Dalsze ogrzewanie próbki prowadziło do topnienia substancji w temperaturze Tm1 = 234.7 K.
Temperatura topnienia, podczas tak przeprowadzonego pomiaru, jest niższa niż w przypadku „kontrolowanego” ochładzania próbki z zadanym tempem, które wynosiło 1-10 K/min, przy czym Tm =250.8 K. Uzyskane wartości temperatur topnienia 2,2-DM-1-B są różne i
najprawdopodobniej zależą od tego jakiego typu faza stała była ogrzewana.
Pomiary przeprowadzone dla 3,3-DM-1-B na mikrokalorymetrze DSC 7 potwierdziły [Juszyńska i inni, 2006] wcześniej zarejestrowane i opisane wyniki eksperymentalne [Massalska – Arodź i inni, 2004]. Na rysunku 4 przedstawiono krzywą DSC uzyskaną dla 3,3-DM-1-B po szybkim ochłodzeniu do 100 K, podczas którego nie zarejestrowano żadnych zmian w zachowaniu krzywych DSC ogrzewano substancję z tempem ΔT/Δt = 10 K/min. Zarejestrowane zostały wówczas cztery anomalie w temperaturach: 150 K, 196.4 K, 231.5 K, 233.5 K. Anomalia przy temperaturze 150 K została przypisana mięknięciu szkła fazy ciekłej, natomiast anomalia przy 196.4 K spontanicznej krystalizacji przechłodzonej cieczy, która wtedy powstała. Stabilna faza krystaliczna 3,3-DM-1-B uległa topnieniu w 231.5 K, natomiast w temperaturze o 2 K wyższej widoczna jest kolejna mała anomalia związana prawdopodobnie z pewnym zanieczyszczeniem próbki. Jednakże we wcześniejszych pomiarach DSC opisanych w pracy [Massalska-Arodź, 2004] małą anomalię, która towarzyszyła topnieniu zaobserwowanemu w temperaturze 230 K od strony niższych temperatur. 1 4 0 1 6 0 1 80 2 0 0 2 2 0 2 4 0 2 6 0 28 0 0 2 0 4 0 6 0 8 0 1 0 0 Δ W [mW] Temperatura [K] 1 0 K /m in
Rysunek II.4. Termogram DSC otrzymany podczas ogrzewania substancji 3,3-dwumetylo-1-butanolu [Juszyńska i inni, 2006].
Takie położenie piku mogłoby być spowodowane topnieniem metastabilnej fazy, której domieszka mogła współistnieć poniżej tej anomalii.
Natomiast pomiary krzywych przepływu ciepła w jednostce czasu w zależności od temperatury przeprowadzone z szybkością ochładzania ΔT/Δt = 5 K/min taką jak w pracy [Massalska-Arodź i inni, 2004], potwierdziły uzyskany wcześniej rezultat: podczas ochładzania zarejestrowano w temperaturze T = 195 K krystalizację przechłodzonej cieczy izotropowej, natomiast podczas ogrzewania jedynie pojedynczą endotermiczną anomalię odpowiadającą za topnienie fazy krystalicznej.
Na rysunku II.5 zaprezentowany został rezultat pomiarów dla 3,3-DM-2-B uzyskany podczas ochładzania i ogrzewania próbki ze stałym tempem ΔT/Δt = 10 K/min. Podczas ochładzania zaobserwowano egzotermiczną anomalię w temperaturze Tc = 260 K, związaną z
krystalizacją przechłodzonej cieczy izotropowej do fazy plastycznej, która ulega zaszkleniu w
160 180 200 220 240 260 280 300 0 20 40 60 80 100 Δ W [mW] Temperatura [K] 10 K/ min
Rysunek II.5. Termogram DSC otrzymany podczas ochładzania (niebieska krzywa) i ogrzewania (czerwona krzywa) 3,3-dwumetylo-2-butanolu [Juszyńska i inni, 2006].
temperaturze 210 K dając zmianę rejestrowanego przepływu ciepła o typowym schodkowym kształcie [Littleton i Roberts 1920; Yamamoto, 1964, 1965]. Jednak podczas ogrzewania nie udało się zaobserwować mięknięcia szkła fazy plastycznej, lecz jedynie endotermiczne anomalie. Przy T3 = 249.9 K obserwowano pojedyncze przejście typu „ciało stałe - ciało
stałe”, które może być opisane jako przejście pomiędzy fazami stałymi o różnym nieporządku. Przy dalszym ogrzewaniu obserwowano „zachodzące na siebie” endotermiczne anomalie w temperaturach: T2 = 271.7 K i T1 = 274.3 K, Tm = 275 K, z których ostatnia jest
związana z topnieniem krystalicznej fazy plastycznej do cieczy izotropowej. Sekwencja faz uzyskanych w pomiarach DSC została potwierdzona metodą kalorymetrii adiabatycznej
(rozdział II. 2). Dla porównania temperatury przejść fazowych uzyskanych metodą kalorymetrii adiabatycznej są następujące: T3 = 239 K, T2 = 255.6 K i T1 = 264 K, Tm = 275.5
K.
Krzywe termiczne dla czwartego izomeru 2,3-DM-2-B przedstawiono na rysunku II.6a i b. W trakcie ochładzania z tempem ΔT/Δt = 10 K/min, zarejestrowano krystalizację przechłodzonej cieczy izotropowej w temperaturze Tc = 231 K (rys. II.6a). Podczas
ogrzewania (ΔT/Δt = 10 K/min) zaobserwowano anomalie w temperaturach T1 = 248.6 K i Tm
=259.7 K, związane najprawdopodobniej z topnieniem mieszaniny faz krystalicznych.
160 180 200 220 240 260 280 0 20 40 60 80 100 Δ W [mW] Temperatura [K] 10 K/ min 220 230 240 250 260 270 0 20 40 60 80 100 Δ W [mW ] Temperatura[K] 10 K/min (a) (b)
Rysunek II.6. Termogram DSC otrzymany podczas ochładzania (niebieska krzywa) i ogrzewania (czerwona krzywa) 2,3-dwumethylo-2-butanolu (a) oraz wykres przepływu ciepła w zależności od temperatury podczas ogrzewania po raptownym ochłodzeniu próbki do temperatury 223 K (b) [Juszyńska i inni, 2006].
Natomiast raptowne ochłodzenie 2,3-DM-2-B do temperatury około 223 K doprowadziło do zarejestrowania podczas ogrzewania spontanicznej krystalizacji przechłodzonej fazy izotropowej. Dalsze ogrzewania pozwoliło zaobserwować topnienie mieszaniny dwóch faz stałych (rys. II.6b), które objawia się poprzez złożoną anomalię. Wartości temperatur przejść fazowych uzyskanych w pomiarze, którego wynik widoczny jest na rys.II.6b są następujące Tcc = 225 K, T1 = 251.4 K i Tm = 260 K.
Na rysunku II.7 naniesiono tak zwane „temperatury pikowe” przejść fazowych w zależności od tempa ΔT/Δt ochładzania i ogrzewania substancji. Temperatury typu „onset” (temperatura, w której rejestruje się początek przemiany fazowej) byłyby trudne do wyznaczenia ze względu na zbyt małe odległości temperatur przejść np. dla 3,3-DM-2-B,
gdzie poszczególne anomalie zaobserwowane przy ogrzewaniu nachodzą na siebie. Wartości temperatur topnienia dla 2-butanoli o bardziej globularnych molekułach są wyższe od wartości uzyskanych dla 1-butanoli, które posiadają molekuły bardziej zbliżone do elipsoidalnych. Spontaniczną krystalizację przechłodzonej fazy ciekłej uzyskałam w trakcie ogrzewania dla trzech izomerów 2,2-DM-1-B, 3,3-DM-1-B i 2,3-DM-2-B .
0 5 10 15 20 180 200 220 240 260 280 Temperatura [K ] dT/dt [K/min]
Rysunek II.7. Zależność temperatury topnienia (linia czerwona i puste symbole) i krystalizacji (linia niebieska i pełne symbole) substancji: 2,2-dwumetylo-1-butanol (▲,Δ), 3,3-dwumetylo-1-butanol (○, ●), 3,3-dwumethylo-2-butanol (■, □), 2,3-dwumethylo-2-butanol (♦, ◊). Krystalizacja dla 3,3-dwumetylo-1-butanol zarejestrowana była podczas ogrzewania (niebieska linia przerywana) [Juszyńska i inni, 2006].
W Tabeli II.1 i II.2 zestawione zostały temperatury przejść fazowych Tp podczas
ochładzania (Tabela II.1) i ogrzewania (Tabela II.2) wraz z ich wartościami zmian entalpii i entropii. Pola powierzchni pod każdą anomalią na uzyskanych termogramach wyliczono względem linii bazowej i dostarczają informacji o całkowitych efektach cieplnych wywołanych zmianami zachodzącymi w próbkach. Wartości entalpii przejścia ΔH wyliczono stosując równanie II.1. Natomiast korzystając z równania II.2
p
T H S = Δ
Δ (II.2)
wyliczono wartości entropii ΔS przejść fazowych dwumetylobutanoli. Małe wartości entalpii topnienia alkoholi 2,2-DM-1-B, 3,3-DM-1-B i 3,3-DM-2-B sugerują, że topnienie substancji następowało z fazy o znacznym nieporządku molekuł do fazy o jeszcze większym nieporządku molekuł. Uzyskane wartości zmiany entropii spełniają kryterium Timmermansa
Tabela II.1. Termodynamiczne parametry charakterystycznych temperatur przemian fazowych (krystalizacja Tc, przejście szkliste Tg) oraz ich wartości zmian entalpii ΔH i
entropii ΔS (±10 %) dla badanych izomerów podczas ochładzania z tempem ΔT/Δt = 10 K/min. W nawiasie znajdują się literaturowe temperatury przejść fazowych: [1] Chan i Johari 1974;[2] Edelmann, 1990, i inni 1991; [3] Massalska – Arodź i inni, 2004.
Substancja TC [K] Tg [K] 2,2-DM-1-B 218.92* 212 ΔH=661 ΔS=3.1 (163 [1]) (158 [2]) 3,3-DM-1-B (cc)188a 186.5a 196.44*a ΔH=4798 ΔS=24.4 (156a [3]) 144.9a 150.6*a 3,3-DM-2-B 267.6* 260 ΔH=5596 ΔS=21.5 220* 213 2,3-DM-2-B 233.8* 231±1 ΔH=8814.6 ΔS=38
[ΔH] = [J/g], [ΔS] = [J/g K], symbol * oznacza temperatury przejść fazowych ekstrapolowane do zerowego tempa zmian temperatury w próbce, symbol a oznacza temperatury anomalii zarejestrowanej podczas ogrzewania.
Tabela II.2. Termodynamiczne parametry charakterystycznych temperatur przemian fazowych (faza stała- faza stała, topnienie Tm) oraz ich wartości zmian entalpii ΔH i entropii
ΔS (±10 %) dla badanych izomerów podczas ogrzewania z tempem ΔT/Δt = 10 K/min. W tabeli przedstawiono również temperatury przejść fazowych wyznaczone przez: [1] Dannhauser, 1965; [2] Chan i Johari 1974; [3] Edelmann, 1990, i inni 1991; [4] Massalska– Arodź i inni, 2004. Substancja T3 [K] T2 [K] T1 [K] Tm [K] 2,2-DM-1-B 187.9 198.6 210.4 234.26* 235.5 ΔH=847 ΔS=3.6 (241 [1,2]) (250.6 [3]) 250.03* 250.8 ΔH=585.5 ΔS=2.3 3,3-DM-1-B 234 [4] 230* 231.5 ΔH=5712.6 ΔS=24.7 3,3-DM-2-B 249.9* 249 ΔH=119.5 ΔS=0.4783 271,7* 274,3* 275.5* 275 ΔH=7209.5 ΔS=26. 2 2,3-DM-2-B 248.63* 257.5* 259.7 ΔH=10441.2 ΔS=40.2
[ΔH]=[J/g], [ΔS]=[J/g K], symbol * oznacza temperatury przejść fazowych ekstrapolowane do zerowego tempa zmian temperatury w próbce.
[Timmermans, 1961], które mówi, że z topnieniem fazy plastycznej mamy do czynienia jeżeli wartość ΔS jest mniejsza od 21 kcal/mol. Sugeruje to, że następowało topnienie fazy rotacyjnej. Duża wartość entropii topnienia odnotowana dla 2,3-DM-2-B odpowiada przemianie z fazy krystalicznej o wysokim uporządkowaniu molekuł do fazy ciekłej o wysokim nieporządku molekuł izomeru.
Badania DSC dwumetylobutanoli pozwoliły na otrzymanie fazy szklistej dwóch izomerów tj. dla 3,3-DM-1-B, 3,3-DM-2-B. Natomiast dane literaturowe dostarczają informacji, że 2,2-DM-1-B również wykazuje tendencję do tworzenia szkła fazy plastycznej.
Potwierdzenie faz termodynamicznych otrzymanych metodą DSC uzyskano przeprowadzając badania z zastosowaniem metody bardzo czułej na wykrywanie nawet faz metastabilnych, a mianowicie metody kalorymetrii adiabatycznej.
II. 2. Kalorymetria adiabatyczna
Kalorymetria jest metodą badań ciała stałego, która pozwala na śledzenie efektów cieplnych jakie towarzyszą przemianom fazowym w substancjach chemicznych poddanych ogrzewaniu. Pomiar temperaturowej zależności pojemności cieplnej C(T) substancji daje możliwość obserwacji kinetyki i określenia charakteru przejść fazowych oraz oszacowania parametrów termodynamicznych takich jak entalpia H, entropia S oraz energia wewnętrzna U i entalpia swobodna Gibbsa G dla tych przejść.
Kalorymetr adiabatyczny jest kalorymetrem nieizotermicznym, w którym temperatura końcowa procesu cieplnego różni się od temperatury początkowej, przy czym wymiana energii z otoczeniem jest minimalizowana. Fenomenologiczna definicja ciepła właściwego przy stałym ciśnieniu Cp lub przy stałej objętości Cv jest określona w warunkach równowagi
termodynamicznej badanej próbki w następujący sposób ; 1 P p p T H m C ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = V p T U m C ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = 1 v , (II.3)
gdzie mp oznacza masę próbki. Dla ciał stałych (w przeciwieństwie do gazów) różnica
pomiędzy Cp a Cv jest niewielka, gdyż ich rozszerzalność cieplna jest znikoma.
Pomiary ciepła właściwego przy użyciu kalorymetru adiabatycznego polegają na dostarczeniu do odizolowanego od otoczenia naczynia z próbką określonej ilości energii cieplnej Δ i pomiar przyrostu temperatury TQ Δ . Mierzona pojemność cieplna C(T) wyraża się następującym wzorem
T Q T C m T C T C p p Δ Δ = + = ( ) ( ) ) ( 0 , (II.4)
gdzie C0(T) jest pojemnością cieplną naczynia kalorymetrycznego. W czasie eksperymentów,
gdy objętość próbki ulega zmianie, mierzone eksperymentalnie ciepło właściwe Cp(T) można
interpretować jako podatność substancji na dostarczenie do niego energii Δ , przy czym Q odpowiedź układu to przyrost temperatury. Wyliczoną wartość ciepła właściwego Cp(T)
przypisuje się temperaturze średniej T z zakresu TΔ , co można zapisać następująco
2 2 k p p T T T T T = +Δ = + , ΔT =Tk −Tp. (II.5) Wyznaczenie ciepła właściwego Cp(T) badanej substancji wymaga uwzględnienia pojemności
cieplnej C0(T) pustego naczynka bez próbki.
Badania kalorymetryczne można przeprowadzać na dwa sposoby. Pierwszym z nich jest klasyczna metoda adiabatyczna, żargonowo nazywana metodą punktową, w której w trakcie ogrzewania substancji otrzymujemy bezwzględne wartości ciepła właściwego w poszczególnych temperaturach wybranego do badań zakresu. Liczba punktów uzyskanych w takim eksperymencie zależy od ilości ciepła dostarczonego w kolejnych ogrzewaniach i przemian zachodzących w próbce. Drugim sposobem pomiaru jest metoda pseudo DTA, żargonowo zwana metodą „dryftową”, polegająca na wyznaczaniu pochodnej temperatury względem czasu w funkcji czasu przy warunku stałej porcji ciepła dostarczanej w jednostce czasu do próbki. Wówczas
t Tt Q T Q T C T C Δ ΔΔ Δ = Δ Δ = − ( ) ) ( 0 , (II.6)
przy czym t to czas. Przy założeniu ΔQ Δt =const, równanie II.6 przyjmuje postać ; ) ( ) ( ) ( 0 T C T C const T t T − = Δ Δ (II.7)
W eksperymencie z użyciem metody „dryftowej” wielkością mierzoną jest ΔT Δt(T). Metoda ta dostarcza jakościowej informacji o anomaliach (zmianach) ciepła właściwego nie tylko w trakcie ogrzewania, ale również w trakcie ochładzania próbki. Ochładzanie i ogrzewanie zachodzi w sposób ciągły, ze stałą prędkością Δ /Q Δt. Jest to metoda dynamiczna - w trakcie pomiaru badana substancja nie znajduje się w stanie równowagi termodynamicznej. Metoda dryftowa dostarcza informacji nie tylko o przejściach fazowych, ale również o takich efektach termicznych jak: histereza temperaturowa, przegrzanie czy
przechłodzenie badanej fazy termodynamicznej. Istotnym jest to, że metoda ta pozwala wykrywać subtelne efekty cieplne (anomalie) oraz bardzo dokładnie oszacować temperatury przejść fazowych (szczególnie temperaturę Tg) i opisać kinetykę przemian fazowych.
Kalorymetr adiabatyczny umożliwia badanie bardzo powolnych procesów takich jak np. relaksacja entalpii w okolicy przejścia szklistego mogących trwać wiele godzin, a nawet dni. Faza metastabilna zmierza bardzo wolno do równowagi termodynamicznej. Relaksację entalpii takiego układu termodynamicznego można obserwować poprzez zmiany jego temperatury czyli samoogrzewanie lub samochładzanie próbki [Kohlrausch, 1954; Gumiński, 1964; Suga i Seki, 1979] β τ ⎟⎠ ⎞ ⎜ ⎝ ⎛ − − ∞ =T B t t T( ) ( ) exp , (II.8)
gdzie T(∞) jest temperaturą równowagi, τ jest czasem relaksacji, parametr 1-β jest miarą kooperacyjności dynamiki molekuł układu.
Kalorymetr pozwala również na obserwację krystalizacji. Powstawanie fazy krystalicznej jest zjawiskiem złożonym. W trakcie przemiany fazowej (krystalizacji) zachodzą dwa następujące po sobie procesy, najpierw nukleacja zarodków nowej fazy, a następnie ich wzrost. Przy powstawaniu nowej fazy energia dla procesu nukleacji jest znacznie wyższa niż w przypadku procesu wzrostu. Krzywa tempa nukleacji w funkcji temperatury ma maksimum poniżej analogicznej krzywej dla wzrostu zarodków nowej fazy.
Fazy stałe badanych DM-B występują w kilku odmianach polimorficznych. Można wyróżnić dwa typy polimorfizmu: enancjotropowy i monotropowy. Enancjotropowy układ przejść fazowych jest obserwowany dla stabilnych faz termodynamicznych występujących w ściśle określonych niezachodzących na siebie zakresach temperatur. Monotropowy układ przejść fazowych cechuje to, że jest on odmienny przy ochładzaniu i przy ogrzewaniu. Różne rodzaje przejść fazowych zostały sklasyfikowane przez Ehrenfesta [Robert i Theodore 1979].
Przejścia fazowe I-go rodzaju charakteryzuje skokowa zmiana entropii i objętości, współistnienie dwóch sąsiednich faz w punkcie przemiany, występowanie ciepła utajonego przemiany oraz możliwość uzyskania fazy termodynamicznie niestabilnej np. poprzez przechłodzenie fazy wysokotemperaturowej. Bardzo ważne miejsce w naszych badaniach zajmują przemiany typu porządek-nieporządek (przemiany II-go rodzaju), które polegają na tym, że w fazie niskotemperaturowej występuje pewien rodzaj uporządkowania, którego brak jest w fazie wyżej temperaturowej. Stan nieporządku wynika: ze swobody przemieszczeń środków ciężkości molekuł przy równoczesnej swobodzie zmian orientacji molekuł jak w
fazach ciekłych; ze swobody zmian orientacji molekuł - jest to tzw. nieporządek orientacyjny jaki występuje w krystalicznych fazach plastycznych; ze swobody przemieszczenia środków ciężkości atomów lub molekuł (tzw. nieporządek pozycyjny, jaki występuje w anizotropowych fazach ciekłokrystalicznych); oraz ze zmian konformacji wewnętrznej molekuł (tzw. nieporządek konformacyjny molekuł w niektórych fazach krystalicznych).
Miarą nieporządku jest entropia. Jeżeli skok entropii w przejściu fazowym jest duży (>> 21 J/mol K) to świadczy to o przejściu z fazy dobrze uporządkowanej (kryształ) do fazy nieuporządkowanej (ciecz). Jeżeli zaś skok entropii przyjmuje wartość ≈ 21 J/mol K lub mniejszą to mamy do czynienia z przejściem z częściowo uporządkowanej fazy, np. fazy plastycznej, do fazy nieuporządkowanej (cieczy). Entalpia swobodna G (potencjał termodynamiczny Gibbsa) zdefiniowana jako
) ( ) ( ) (T H T T S T G =Δ − Δ Δ , (II.9)
określa stabilność faz termodynamicznych. W układzie enencjotropowym entropia S(T) fazy wyżej temperaturowej jest wyższa. W danym zakresie temperatur stabilna jest faza o najmniejszym G(T).
II. 2. 1. Budowa kalorymetru adiabatycznego
Pomiary z zastosowaniem kalorymetrii adiabatycznej zostały wykonane na układzie pomiarowym zaprojektowanym i wykonanym w Zakładzie Badań Strukturalnych IFJ PAN. Kalorymetr pozwala wyznaczyć m.in. ciepło właściwe substancji w szerokim zakresie temperatur od temperatur azotowych do ok. 300 K. Naczynie z próbką (rys. II. 8, 9) zawieszone jest na jedwabnej nici wewnątrz osłony adiabatycznej, która jest umieszczona w tzw. wolno wiszącej osłonie radiacyjnej. Próbka wraz z osłonami znajduje się w tzw. zbiorniku wewnętrznym, na końcu ramienia, na którym umocowane są cylindry radiacyjne. Cały układ umieszczony jest w kriostacie, stalowym, próżnioszczelnym płaszczu otaczającym zbiornik wypełniony cieczą kriogeniczną (azot). Aby zmniejszyć wymianę ciepła z otoczeniem, w przestrzeni wewnętrznej płaszcza panuje próżnia rzędu 10-3 mbar, podczas gdy w zbiorniku wewnętrznym panuje próżnia rzędu 10-5 mbar. Osłona wolno wisząca zapobiega powstawaniu gradientów temperatury na osłonie adiabatycznej, jakie mogłyby powstać z powodu sąsiedztwa ze zbiornikiem kriogenicznym. Osłona adiabatyczna ma taki sam cylindryczny kształt jak próżnioszczelne i wykonane z miedzi pokrytej złotem naczyńko pomiarowe o pojemność 8 ml. Na zewnętrznej ścianie osłony nawinięty jest grzejnik z drutu
manganinowego podłączony do naczynia pomiarowego obok platynowego termometru oporowego. Dla utrzymania stałości temperatury niezbędnej do wyeliminowania strat ciepła pomiędzy osłoną adiabatyczną a naczyńkiem pomiarowym, zastosowano dodatkowo dwie termopary dwupunktowe. Jedna końcówka termopary jest przymocowana do naczyńka z próbką, a druga do osłony adiabatycznej. Pomiaru ilości ciepła dostarczonego w eksperymencie do naczyńka z próbką dokonuje się poprzez pomiar mocy prądu grzejącego i okresu grzania.
Układ próżniowy kalorymetru składa się z pompy dyfuzyjnej i pompy rotacyjnej oraz z tzw. rezerwuaru próżni wstępnej o objętości 70 l. Niedogodnością w stosowaniu tej metody jest użycie dużej ilości substancji tak, aby jej pojemność cieplna była porównywalna z pojemnością cieplną naczynia kalorymetrycznego. Jednak im większa próbka tym większa dokładność pomiaru ciepła właściwego. Czułość pomiaru temperatury wynosi 10 μK.
Rysunek II.8. Schemat kalorymetru adiabatycznego: 1 - grzejnik, 2 – próbka, 3 - osłona adiabatyczna, 4 - osłona wolno wisząca, 5 – zbiornik wewnętrzny, 6 - zawieszka ekranu, 7 – rurka centralna, 8 – ekran, 9 – płaszcz wewnętrzny, zbiornik azotu, 10 – rurka cieplna, 11 – rurka wewnętrzna w komorze z azotem, 12 – izolacja, 13 – płaszcz próżniowy.
Rysunek II.9. Widok naczyńka kalorymetrycznego wraz z osłoną adiabatyczną po lewej stronie i osłoną wolno-wiszącą po stronie prawej.
Podłączony do układu pomiarowego komputer z oprogramowaniem steruje pomiarem C(T) jak również pozwala na zmiany parametrów eksperymentu. Stosując program Vik, w każdej chwili eksperymentu można wizualizować efekty pomiaru.
Pomiary metodą „dryftową” polegają na tym, że badana substancja może być ochładzana lub ogrzewana w sposób ciągły poprzez osłonę adiabatyczną, która odpowiednio spełnia rolę chłodnicy lub grzejnika. Temperatury osłon adiabatycznej i wolno-wiszącej są stabilizowane, czyli utrzymywane w stałej różnicy temperatur względem naczynia z próbką poprzez oddzielne regulatory PID w oparciu o sygnały napięciowe z odpowiednich termopar.
Pomiary metodą punktową polegają na tym, że dostarcza się do badanej próbki stałą porcję energii w równych odstępach czasu co powoduje wzrost temperatury. W konsekwencji tego zabiegu można wyznaczyć wartości ciepła właściwego badanej substancji w kolejnych temperaturach. Energia do układu jest dostarczana dzięki grzałce naczynia kalorymetrycznego jak i osłony wolno-wiszącej. Pomiar każdego punktu C(T) jest poprzedzony oczekiwaniem na dojście układu do równowagi w nowej temperaturze. Zazwyczaj w pomiarach stosowaliśmy 4 minutowe ogrzewania po wcześniejszym 16 minutowym oczekiwaniu na równowagę.
Oszacowanie funkcji termodynamicznych w przejściu fazowym wymaga pomiaru zwanego „entalpy run”, który polega na jednym ogrzewaniu w całym zakresie temperatur obejmującym granice występowania anomalii (danego przejścia fazowego).
31 ,5 32,0 3 2,5 33 ,0 33,5 3 4,0 2 38 2 40 2 42 2 44 2 46 2 48 T [K] cza s [h ] 0 50 10 0 15 0 20 0 25 0 30 0 35 0 Δ T/ Δ t [mK/mi n]
Rysunek II.10. Krzywa zależności tempa zmian temperatury („dryftu”) w funkcji czasu zarejestrowana podczas ogrzewania, gdy w układzie nie występują przemiany fazowe. Wzrost temperatury pokazuje krzywa schodkowa.
Po dostarczeniu porcji energii i ustaleniu się równowagi termodynamicznej w układzie (rysunek II.10) nie obserwuje się anomalnych zmian temperatury ani wartości dryftów, pod warunkiem, że w obserwowanym zakresie temperatur nie pojawia się żadna anomalia związana z przejściem fazowym.
W przeprowadzonych pomiarach kalorymetrycznych zostały użyte następujące masy próbek: dla 2,2-DM-1-B było to 5.5279 g, dla 3,3-DM-2-B to 6.1349 g zaś dla 2,3-DM-2-B to 6.6007 g, przy czym masa molowa każdego izomeru wynosi 102.17476 g/mol. Każda próbka była badana w kilkunastu seriach pomiarowych.
II. 2.2. Obliczenia funkcji termodynamicznych
Pomiary temperaturowych zmian pojemności cieplnej pozwalają ustalić wartości temperatur przejść fazowych oraz obliczyć temperaturowe zależności funkcji termodynamicznych, tj. entalpii H i entropii S oraz entalpii swobodnej Gibbsa G (wzór II.9) w poszczególnych fazach termodynamicznych.
Wartości entalpii ΔH(T) niskotemperaturowych faz krystalicznych obserwowanych dla izomerów neoheksanolu zostały obliczone przy użyciu zależności
dT T C H k p T T p( )
∫
= Δ . (II.10)Zmianę entropii ΔS jaka towarzyszy zmianie temperatury od Tp do Tk obliczono korzystając
z zależności [Atkins, 1999; Demichowicz-Pigoniowa, 1980]
∫
= Δ k p T T p T dT T C S ( ) . (II.11)Na rysunkach II.9, II.11 oraz II.14 ΔH(T) oraz ΔS(T) dotyczą entalpii oraz entropii w temperaturze T określonej przez równanie II.5. W poszczególnych fazach uzyskano dla ΔH(T) i ΔS(T) różne zależności od temperatury. Przy przejściu fazowym w temperaturze Tf
obserwowano anomalię na krzywej Cp(T), której odpowiada skokowy wzrost wartości entalpii
H
Δ oraz entropii ΔS. Dokonując obliczeń entalpii swobodnej∆G(T) dla poszczególnych faz otrzymałam diagramy fazowe dla badanych izomerów. Dla każdej substancji pomiary punktów ciepła właściwego, poprzez bezpośredni pomiar pojemności cieplnej, przeprowadzone zostały podczas ogrzewania próbki zarówno po wolnym jak i po gwałtownym ochłodzeniu helem od temperatury pokojowej do 100 K. Obserwacje zmian zachodzących w badanych próbkach zarówno w trakcie ogrzewania jak i ochładzania umożliwiła metoda „dryftowa”. Dzięki temu było wiadomo czy raptowne ochładzanie substancji prowadziło najpierw do jej krystalizacji do fazy plastycznej, która uległa zaszkleniu czyli też do zeszklenia fazy ciekłej.
Dotychczas tylko jeden spośród czterech izomerów neohekasanolu tj. 3,3-DM-1-B został przebadany metodą kalorymetrii adiabatycznej, a wyniki eksperymentu zostały opisane w pracy Massalska–Arodź i inni, 2004. Pomiary pojemności cieplnej 3,3-DM-1-B przy zastosowaniu kalorymetru adiabatycznego przeprowadzone zostały w zakresie temperatur od 13 K do 302 K. Rezultatem pomiarów było uzyskanie szkła cieczy izotropowej, które ulega mięknięciu transformując w temperaturze Tg = 146 K do przechłodzonej fazy ciekłej, z której
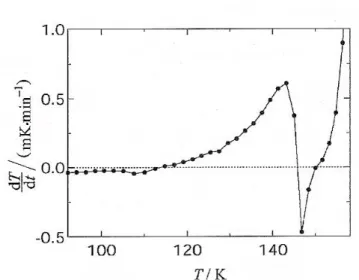
to szkło powstało. Zastosowana metoda dryftowa, czyli pomiar temperaturowej zależności tempa zmian temperatury w próbce czyli dryftu dT/dt(t) pozwoliła na określenie dokładnej temperatury przejścia szklistego - patrz rys.II.11 i II.12.
Przyjmując, że w stanie równowagi termodynamicznej dT/dt jest bardzo bliskie zera, a odstępstwa od tej wartości sugerują pojawienie się anomalii termodynamicznej, transformację w temperaturze Tg określa zmiana „znaku” dryftów z wartości dodatnich na ujemne. Przejście
Rysunek II.11. Relaksacja entalpii w okolicy przejścia szklistego obserwowana poprzez zmianę temperaturowej zależności tempa zmian temperatury (dryft) w 3,3-DM-1-B. Przejście dryftu przez zero pozwala wyznaczyć wartość Tg [Massalska-Arodź i inni, 2004].
właściwego ~ 45 J/mol K w zakresie temperatur od 110 K do 143 K, przy czym przejście szkliste pozbawione jest skokowej zmiany entropii. Podczas dalszego ogrzewania. zaobserwowano krystalizację przechłodzonej cieczy co spowodowało brak punktów pomiarowych dla cieczy w pewnym zakresie temperatur. Całkowita krystalizacja pozwoliła uzyskać stabilną fazę krystaliczną, która topi się w temperaturze Tm = 235.68 K. Oszacowane
wartości entalpii i entropii topnienia wynoszą odpowiednio: Δ = 9.54 kJ/mol, H ΔS = 40.9 J/mol K. Zatem topnieniu uległa dobrze uporządkowana faza krystaliczna. Skok entropii w trakcie procesu topnienia jest miarą nieuporządkowana molekuł w fazie cieczy w stosunku do fazy krystalicznej (Rys. II.12). Alkohol 3,3-DM-1-B został jako jedyny zbadany w bardzo szerokim przedziale temperatur do 13 K. Miarą nieporządku rozłożenia molekuł w fazie szklistej jest tzw. entropia konfiguracyjna Sc(0) w temperaturze 0 K zwana entropią
resztkową. Aproksymacja krzywej Sg(T) fazy szklistej pomniejszona o Sk(T) fazy
krystalicznej (uzyskanej przy wolnym ochładzaniu) pozwoliła określić wartość entropii Sc(0)
= Sg(0) - Sk(0) = 4.9 J/mol K. Autorzy pracy oszacowali dla 3,3-DM-1-B temperaturę T0=125
K, poniżej której przechłodzona nieuporządkowana faza cieczy miałaby mniejszą wartość entropii niż uporządkowana faza krystaliczna. Aby zapobiec takiemu paradoksowi, zwanemu paradoksem Kauzmanna [Kauzmann, 1948] musi nastąpić przejście cieczy do szkła powyżej temperatury T0. Zatem poniżej T0 faza szklista nie może powstać. Sprawdzając poprawność
Rysunek II.12. Wykres entropii w funkcji temperatury dla faz termodynamicznych 3,3-DM-1-B [Massalska-Arodź i inni, 2004].
II. 2.3. Pomiary kalorymetryczne dla trzech izomerów neoheksanolu
Pomiary pojemności cieplnej dla trzech izomerów dwumetylobutanoli zostały podjęte w celu potwierdzenia polimorfizmu fazy stałej i oszacowania temperatur przejść fazowych oraz zmian entropii jakie im towarzyszą. Wyniki Cp(T) dla trzech izomerów są zebrane w
Dodatku 3.
Pomiary kalorymetryczne 2,2-DM-1-B były wykonywane kilkukrotnie, zarówno podczas szybkiego ochładzania substancji oparami helu, wolnego ochładzania osłonami okalającymi naczyńko z próbką, jak również podczas ogrzewania po wolnym i szybkim ochładzaniu.
Podczas szybkiego ochładzania próbki aby uzyskać szkło fazy ciekłej nie udało się uniknąć krystalizacji. Na rysunku II.13 zaprezentowana jest krzywa dryftowa uzyskana podczas szybkiego ochładzania 2,2-DM-1-B z szybkością 5 K/min. Przegięcie na krzywej zmian dT/dt w funkcji czasu odpowiada za krystalizację przechłodzonej cieczy izotropowej do fazy plastycznej w temperaturze Tc = 181 K, którą odczytujemy z czerwonej krzywej T(t).
W trakcie zachodzenia krystalizacji przechłodzonej cieczy izotropowej mamy do czynienia z procesem egzotermicznym, podczas którego badana próbka oddaje ciepło do układu, co
Ciecz Szkło Cieczy Kryształ Przechłodzona Ciecz
odzwierciedla niewielki wzrost temperatury (widoczny dopiero przy znacznym powiększeniu) w okolicy przegięcia na krzywej zmian dT/dt(t). Zbliżona wartość temperatury krystalizacji przechłodzonej cieczy do fazy plastycznej, Tc = 183 K, została uzyskana metodą DTA i
opisana przez Chana i Johariego [Chan i Johari, 1974], a także metodą DSC (Tc = 179 K) po
szybkim ochładzaniu próbki do 150 K (rys.II.3b). Dalsze szybkie ochładzanie 2,2-DM-1-B doprowadziło do uzyskania, w znacznie niższej temperaturze, fazy szklistej; jest to faza szklista plastycznego kryształu. Temperaturę przejścia szklistego Tg = 123 K mogłam wyznaczyć na podstawie danych otrzymanych metodą dynamiczną („dryftową”) podczas ogrzewania.
0 20 40 60 -7000 -6000 -5000 -4000 -3000 -2000 -1000 0 0 20 40 60 100 120 140 160 180 200 220 240 260 280 300 Te mp e ratura [K] czas [s] dT /dt [mK/ mi n]
Rysunek II.13. Krzywa zależności tempa zmian temperatury w funkcji czasu dla 2,2-DM-1-B. Temperaturę pokazuje czerwona krzywa.
Temperatura Tg = 163 K podana przez Chana i Johariego oraz Tg = 158 K uzyskana
przez Edelmanna pomiarach DTA znacznie różnią się od temperatury Tg uzyskanej przeze
mnie metodą dryftową w kalorymetrze adiabatycznym.
Na rysunku II.14 przedstawiona jest temperaturowa zależność ciepła właściwego, otrzymana dla 2,2-DM-1-B w dwóch seriach pomiarowych metodą punktową (punkty czarne i czerwone). Dla próbki wcześniej wolno ochłodzonej, w zakresie temperatur od 100 K do 320 K zarejestrowano trzy anomalie ciepła właściwego (czarne punkty). Dwie spośród nich (niskotemperaturowe) przy ok. 195 K i 209 K związane są z przejściami fazowymi pomiędzy trzema różnymi fazami stałymi, natomiast trzecia przy ok. 233 K to topnienie fazy C1. W porównaniu do C (T) dla fazy krystalicznej C3 uzyskanej dla próbki wcześniej wolno
ochładzanej, dla próbki szybko ochładzanej zaobserwowano wyraźny wzrost Cp(T) w okolicy
Tg (punkty czerwone, rysunek II.14 okienko). Odpowiada on mięknięciu szkła fazy
plastycznej GC2 do fazy C2, która uległa zeszkleniu przy gwałtownym ochładzaniu. Następnie, przy dalszym ogrzewaniu próbki, faza plastyczna C2 przechodzi do fazy krystalicznej C3 w temperaturze 148 K. W temperaturze 195 K, dla obu reżimów pomiaru (punkty czarne i czerwone), obserwowana jest anomalia dająca duży efekt cieplny, co oznacza, że ciepło jest silnie pochłaniane przez próbkę. Tak duży efekt cieplny związany jest z przejściem dobrze uporządkowanej fazy krystalicznej C3 do plastycznej fazy krystalicznej C2, co potwierdza duża wartość skoku entropii ΔS (Tabela III.3).
100 150 200 250 300 0 1000 26000 27000 28000 100 120 140 160 300 350 400 450 Cp [J / m o l K ] Temperatura [K] C p [J/ mo l K ] Temperatura [K] GC2 C3 C2 I C1 C2 C3 C3 GC2 C2
Rysunek II.14. Wykres zależności ciepła właściwego od temperatury dla 2,2-DM-1-B. Punkty czerwone otrzymane po szybkim ochładzaniu próbki, punkty czarne otrzymane po wolnym ochładzaniu próbki. Ciepło właściwe obliczono na mol badanej substancji.
Kolejna anomalia, która pojawia się w temperaturze 209 K jest związana z przejściem fazowym C2→C1. Obserwowany efekt cieplny związany z tym przejściem fazowym jest znacznie mniejszy od obserwowanego w niższej temperaturze. Przejście fazowe C2→C1 jest transformacją pomiędzy dwoma fazami plastyczno – krystalicznymi, przy czym faza wyżej temperaturowa jest fazą, w której molekuły 2,2-DM-1-B wykazują większy nieporządek orientacyjny. Na silny nieporządek w fazie C1 wskazuje mała, w porównaniu z pozostałymi,
anomalia odpowiadająca za topnienie tej fazy przy Tm1 = 233 K. W tabeli II.3 zestawione są
wartości temperatur oraz zmian entalpii HΔ i entropiiΔS dla trzech przejść fazowych dla 2,2-DM-1-B.
Gdy porównujemy temperatury przejść fazowych uzyskane przez Edelmanna metodą DTA z wynikami przedstawionymi w niniejszej pracy zwraca uwagę fakt, że nie obserwował on fazy, która ulegała topnieniu kalorymetrze w temperaturze Tm1. Przejście fazowe C3→C2
uzyskał on w temperaturze 198.6 K, a C2→C1 w temperaturze 210. 4 K, podobnie jak w naszych pomiarach. Edelmann uzyskał dodatkowo przejścia z dwóch różnych faz metastabilnych C3’ i C3’’ do fazy C2 w temperaturach 187.9 K i 196.4 K. W przeprowadzonych przeze mnie pomiarach tych faz nie obserwowałam. Najprawdopodobniej zostały one wyhodowane w warunkach wysokiego ciśnienia.
Tabela II.3. Parametry przejść fazowych dla 2,2-DM-1-B
Przejście fazowe faza C3-faza C2 faza C2-faza C1 faza C1-ciecz T [K] H Δ [J/mol] S Δ [J/mol K] 194,9151 5772,58 29,61 209,19 2689,13 12,85 233,11 4414,9 17,86
Zmiana entropii przejścia z fazy C3 do fazy C2 wynosząca ΔS = 29.61 [J/mol K] potwierdza, że próbka która była wolno ochładzana od fazy ciekłej uległa transformacji do dobrze uporządkowanej fazy krystalicznej C3. Podczas ogrzewania następuje przejście z fazy C3 do fazy C2 związane z uruchomieniem reorientacyjnych stopni swobody molekuł czyli przejście z krystalicznej fazy uporządkowanej do innej krystalicznej fazy o pewnym nieporządku orientacyjnych stopni swobody molekuł. Kolejne przejście z fazy C2 do fazy C1 jest przejściem do fazy o znacznie większym nieporządku orientacyjnym molekuł, lecz wciąż uporządkowanie pozycyjne molekuł jest zachowane. Plastyczno-krystaliczna faza C2 przypada na zakres temperatur od 195 K do 209 K. Natomiast faza C1 występuje w zakresie temperatur od 209 do 233 K, przy czym jest to również faza plastyczno - krystaliczna. Jednak tej fazy nie udało się zeszklić. Temperatury przejść fazowych uzyskane w różnych seriach pomiarowych metodą kalorymetrii adiabatycznej były zawsze bardzo zbliżone, niezależnie od szybkości wcześniejszego ochładzania i od tempa ogrzewania badanej próbki. Na wysoko temperaturowe przejścia fazowe nie miało również wpływu to do jakiej temperatury niskotemperaturowej fazy krystalicznej czy szklistej została ochłodzona przechłodzona faza
ciekła 2,2-DM-1-B. Istotną różnicą był uzyskany efekt cieplny podczas ogrzewania. Podczas ogrzewania po wolnym ochładzaniu intensywność anomalii Cp(T) odpowiadająca przejściu
fazowemu C3→C2 jest znacznie mniejsza (mniejszy efekt cieplny) w porównaniu do uzyskanej po szybkim ochłodzeniu, natomiast intensywność anomalii przejścia C2→C1 jest większa w porównaniu do uzyskanej po szybkim ochłodzeniu substancji. Efekt cieplny towarzyszący topnieniu C1→I jest porównywalny dla obu procesów ochładzania. Na rysunku II.15 przedstawiono ΔS(T) i ΔG(T) obliczone w oparciu o wyniki Cp(T) otrzymane w
zakresie temperatur od 100 K do 300 K (czarne punkty).
100 120 140 160 180 200 220 240 260 280 300 0 200 400 S [J / mo l K] Temperatura [K] Tm T1 T2 100 120 140 160 180 200 220 240 260 280 300 G(T ) Temperatura [K] Tm T1 T2 (a) (b)
Rysunek II.15. Zmiana entropii (a) i entalpii swobodnej (b) od temperatury, obliczone dla poszczególnych faz termodynamicznych 2,2-DM-1-B.
Uzyskana w moich pomiarach temperatura topnienia Tm1 = 233 K różni się od wartości
Tm uzyskanych w pomiarach metodą DTA przez Edelmanna (Tm = 250.6 K) i przez
Dannhausera [Dannhauser i inni, 1965]; oraz Chana i Johariego (Tm = 241 K) jak i przez
Dworkina (Tm = 224.5 K) [Dworkin, 1980]. Edelmann wskazuje, że przyczyną różnych
wartości temperatury topnienia jest problem różnej czystości badanej próbki. Im większe zanieczyszczenie próbki tym temperatura topnienia jest niższa. Jednak topnienie w moich pomiarach metodą DSC przebiegało w temperaturze 251 K. To przemawia raczej za hipotezą, że w pomiarach adiabatycznych i DTA oraz DSC topiły się różne fazy (patrz rys. II.3a). Równocześnie warto przypomnieć, że po szybkim ochładzaniu próbki do 150 K topnienie obserwowałam przy 235 K po wcześniejszej krystalizacji przy 179 K (rys. II.3b). Różnica w temperaturze topnienia może być związane z wpływem tempa chłodzenia próbki na rodzaj fazy, której zarodki powstawały przy obniżaniu temperatury. Wydaje się, że sytuacja fazowa dla 2,2-DM-1-B jest bardziej złożona i planowane są dalsze badania.
Rysunek II.16 przedstawia wyniki obserwacji dryftu dla substancji 3,3-DM-2-B w pobliżu przejścia szklistego przy temperaturze Tg = 223 K, które ilustrują relaksację entalpii w
szkle i przechłodzonej fazie plastycznej.
250 500 750 1000 1250 1500 100 150 200 250 300 250 500 750 1000 1250 1500 -8 -4 0 4 8
Temperat
ura [K]
Czas [s]
dT/dt
[mK/
min]
Rysunek II.16. Zmiana „dryftu” w pobliżu przejścia szklistego fazy plastycznej dla 3,3-DM-2-B. Krzywa czerwona pokazuje zmiany temperatury podczas ogrzewania równymi porcjami energii.
Rysunek II.17 przedstawia punkty Cp(T) uzyskane metodą punktową podczas ogrzewania
substancji 3,3-DM-2-B poddanej wcześniejszemu ochładzaniu z tempem 1 mK/min. Próbka wykazuje bogaty polimorfizm fazy stałej. Zostały zarejestrowane trzy przejścia pomiędzy kolejnymi fazami C4→C3, C3→C2 oraz C2→C1 i topnienie fazy C1.
Wartości temperatury poszczególnych przejść fazowych oraz skoku Δ i H ΔS jakie im towarzyszą zebrano w Tabeli II.4. Nie udało się zarejestrować mięknięcia szkła GC4 obserwowanego metodą dryftową. Podczas ogrzewania próbki, w temperaturze 239 K pojawia się anomalia dająca bardzo mały efekt cieplny o charakterze endotermicznym, którą wiążemy z przejściem fazy plastycznej C4 do innej fazy plastycznej C3. Dalsze ogrzewanie powoduje pojawienie się w temperaturze 255 K anomalii odpowiadającej przejściu fazowemu C3→C2 pomiędzy fazami plastyczno-krystalicznymi. Efekt cieplny w tym procesie jest większy od efektu niżej temperaturowego. W trakcie tego przejścia próbka silnie pochłania ciepło, co świadczy o znacznym wzroście nieporządku molekuł. Kolejne przejście C2→C1 jest bardzo słabe. Największy efekt cieplny towarzyszy topnieniu w temperaturze 275 K.
![Rysunek II.2. Diagram fazowy 2,2-DM-1-B [Edelmann, 1990]. Litera S jest skrótem od solid](https://thumb-eu.123doks.com/thumbv2/9liborg/3014081.4518/15.892.223.723.107.565/rysunek-diagram-fazowy-edelmann-litera-jest-skrótem-solid.webp)
![Rysunek II.4. Termogram DSC otrzymany podczas ogrzewania substancji 3,3-dwumetylo-1- 3,3-dwumetylo-1-butanolu [Juszyńska i inni, 2006]](https://thumb-eu.123doks.com/thumbv2/9liborg/3014081.4518/17.892.238.697.786.1084/rysunek-termogram-otrzymany-ogrzewania-substancji-dwumetylo-dwumetylo-juszyńska.webp)
![Rysunek II.12. Wykres entropii w funkcji temperatury dla faz termodynamicznych 3,3-DM-1- 3,3-DM-1-B [Massalska-Arodź i inni, 2004]](https://thumb-eu.123doks.com/thumbv2/9liborg/3014081.4518/31.892.241.709.106.524/rysunek-wykres-entropii-funkcji-temperatury-termodynamicznych-massalska-arodź.webp)
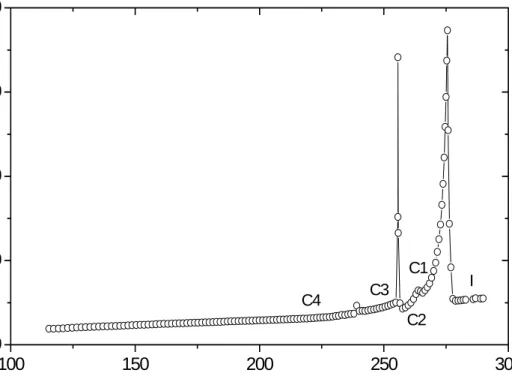
![Rysunek III.2. Temperaturowe zmiany czasów relaksacji obserwowane dla trzech procesów relaksacyjnych w 3,3-DM-1-B [Massalska-Arodz i inni, 2004]](https://thumb-eu.123doks.com/thumbv2/9liborg/3014081.4518/48.892.286.621.369.664/rysunek-temperaturowe-czasów-relaksacji-obserwowane-procesów-relaksacyjnych-massalska.webp)
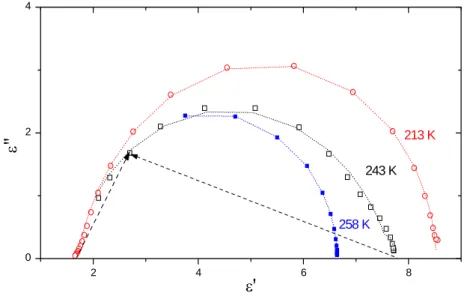
![Rysunek III.3. Diagramy Cole-Cole dla neoheksanolu [Dannhauser i inni, 1965] dla kilku temperatur: 208 K, 225 K, 235 K, 239.5 K, 241.3 K, 247 K, 268 K](https://thumb-eu.123doks.com/thumbv2/9liborg/3014081.4518/49.892.286.616.110.574/rysunek-diagramy-cole-cole-neoheksanolu-dannhauser-kilku-temperatur.webp)