Przyszłość metody elementów skończonych

Klasyczna i izogeometryczna metoda

elementów skończonych

Autorzy:

Maciej Paszynski

Uogólnienie funkcji bazowych poprzez iloczyn tensorowy na 2D Uogólnienie funkcji bazowych poprzez iloczyn tensorowy na 3D Siatki nieregularne

Implementacja w MATLABie generacji funkcji bazowych na podstawie wektora węzłów Rozdział 3. Sformułowania wariacyjne dla różnych problemów i metod

Transport ciepła za pomocą izogeometrycznej metody elementów skończonych Transport ciepła za pomocą tradycyjnej metody elementów skończonych Równania konwekcji-dyfuzji

Problem modelowy przepływu laminarnego (problem Stokesa) Równania liniowej sprężystości

Sformułowania wariacyjne a całkowanie numeryczne Implementacja w MATLABie problemu transportu ciepła

Implementacja w MATLABie problemu adwekcji-dyfuzji metodą Galerkina Rozdział 4. Solwery układów równań liniowych generowanych podczas obliczeń MES

Algorytm eliminacji Gaussa

Algorytm eliminacji Gaussa z pivotingiem Algorytm LU faktoryzacji

Algorytm solwera frontalnego Algorytm solwera wielo-frontalnego Algorytm solwera zmienno-kierunkowego Preconditioner

Algorytm solwera iteracyjnego

Wybór solwera w zależności od rodzaju problemu

Implementacja w MATLABie algorytmu solwera zmienno-kierunkowego dla problemu projekcji bitmapy Rozdział 5. Metody stabilizacji

Stabilizacja metody elementów skończonych

Stabilizacja równań adwekcji-dyfuzji za pomocą metody minimizalizacji reziduum

Stabilizacja równań adwekcji-dyfuzji za pomocą metody Streamline Upwind Petrov-Galerkin (SUPG) Stabilizacja równań Stokesa za za pomocą metody minimalizacji reziduum

Stabilizacja równań Stokesa za za pomocą metody Discontinuous Galerkin (DG) Implementacja w MATLABie problemu adwekcji-dyfuzji ze stabilizacją metodą SUPG

Implementacja w MATLABie problemu adwekcji-dyfuzji za stabilizacją metodą minimalizacji reziduum Rozdział 6. Przetwarzanie siatek obliczeniowych

Generacja i adaptacja siatek obliczeniowych Algorytm h-adaptacji

Algorytm p-adaptacji Algorytm hp-adaptacji

Aproksymacja na siatce z wiszącymi węzłami Analiza izogeometryczna na siatkach adaptacyjnych

Implementacja w MATLABie adaptacyjnego algorytmu projekcji bitmapy

Rozdział 7. Metoda elementów skończonych dla problemów niestacjonarnych i nieliniowych Problemy niestacjonarne

Przykłady operatorów różniczkowych i prawej strony dla różnych niestacjonarnych problemów fizycznych Metoda explicite

Metoda implicite Schemat Cranka-Nicolson Schemat alpha

Przykład niestacjonarnego problemu liniowego: propagacja zanieczyszczeń Implementacja w MATLABie schematu alpha dla problemu transportu ciepła

Przykład niestacjonarnego problemu nieliniowego: przepływ nieliniowy w ośrodku niejednorodnym Rozdział 8. Matematyczne sformułowanie metody elementów skończonych

Przestrzenie funkcyjne

Jednowymiarowy element skończony

Jednowymiarowe sformułowania silne i słabe dla problemu eliptycznego Jednowymiarowa metoda elementów skończonych

Przykład jednowymiarowej metody elementów skończonych Dwuwymiarowy element skończony

Dwuwymiarowe sformułowania silne i słabe dla problemu eliptycznego Dwuwymiarowa metoda elementów skończonych

Algorytm adaptacyjny

Zbieżność metody elementów skończonych Izogeometryczna metoda elementow skonczonych Przyszłość metody elementów skończonych

Wprowadzenie do podręcznika o metodzie

Wprowadzenie do podręcznika o metodzie

elementów skończonych

elementów skończonych

Podręcznik ten przedstawia obszerne wprowadzenie do metody elementów skończonych, z uwzględnieniem metod analizy izogeometrycznej.

Rozdziały uzupełnione są o przykładowe kody MATLABa (możliwe do uruchomienia w darmowej wersji Octave). Autorem tekstu jest prof. dr hab. Maciej Paszyński.

Autorami kodów MATLABa są dr inż. Marcin Łoś oraz dr inż. Maciej Woźniak z Katedry Informatyki z mojego zespołu Algorytmów i Systemów Adaptacyjnych.

Chciałbym bardzo podziękować Panom Maćkowi i Marcinowi za zaawansowane implementacje w MATLABie.

Chciałbym również bardzo podziękować mojej żonie, dr hab. Annie Paszyńskiej z Uniwersytetu Jagiellońskiego za pomoc w przygotowaniu wielu rysunków do podręcznika.

Chciałbym bardzo serdecznie podziękować recenzentom, prof. Maciejowi Pietrzykowi i prof. Krzysztofowi Banasiowi za bardzo wnikliwe przeczytanie książki i szczegółowe recenzje, których uwzględnienie znacznie podniosło poziom podręcznika. Podręcznik mój adresowany jest dla studentów studiów technicznych i informatycznych, i z tego względu koncentruje się na aspektach praktycznych i implementacyjnych poszczególnych zagadnień związanych z metodą elementów skończonych. Podręcznik mój natomiast nie porusza zagadnień matematycznej teorii zbieżności metody elementów skończonych. Czytelników których interesują matematyczne podstawy metody elementów skończonych zachęcam do przeczytania rozdziału

"Matematyczne sformułowanie metody elementów skończonych". Czytelników bardziej zainteresowanych aspektami implementacyjnymi i ogólnym wprowadzeniem do metody elementów skończonych zachęcam do pominięcia tego rozdzaiłu przy pierwszym czytaniu i rozpoczęcia lektury od rozdziału "Przykładowy problem dwuwymiarowej projekcji bitmapy".

Podręcznik ten opisuję zarówno klasyczną metodę elementów skończonych oraz izogeometryczną metodę elementów skończonych. Pierwsze prace naukowe na temat metody elementów skończonych pochodzą z roku 1940 od Richarda Couranta (profesor matematyki, urodzony w Lublińcu w Polsce w roku 1888 na ówczesnym terytorium niemieckim, wyemigrował do USA) i Alexandra Hrennikoffa (profesor inżynierii lądowej, urodzony w Rosji, wyemigrował do Kanady), oraz Feng Kanga w Chinach w roku 1950 [1][2][3]. Metoda ta nabrała impetu w latach 1960-1970 dzięki pracy Olgierda Ziemkiewicza (profesor inżynierii lądowej, żyjącą w Wielkiej Brytanii, o Polskich korzeniach) [4]. W ostatnich latach rosnącą popularnością cieszy się

izogeometryczna metoda elementów skończonych, propagowana przez zespół prof. T. J. R. Hughes'a, stosująca funkcje bazowe z rodziny B-spline, cechujące się ciągłością wyższego stopnia [5]. Równolegle do metod analizy izogeometrycznej rozwijane są metody adaptacyjne, korzystające z klasycznej metody elementów skończonych, stosujące hierarchiczne funkcje bazowe. Algorytmy adaptacyjne pozwalające na eksponencjalną zbieżność dokładności rozwiązania względem rozmiaru siatki obliczeniowej, rozwijane są przez grupę prof. Leszka Demkowicza (polski matematyk i profesor mechaniki, pracujący na Uniwersytecie Teksańskim w Austin) [6][7]. Obserwuje się również próby łączenia metod adaptacyjnych z analizą izogeometryczną, poprzez tworzenie nowych rodzin wielomianów, możliwych do definiowania na siatkach adaptacyjnych, umożliwiających mieszanie wielomianów z rodziny B-spline różnego stopnia [8].

Klasyczna metoda elementów skończonych na siatkach regularnych jest szczególnym przypadkiem izogeometrycznej metody elementów skończonych.

Jedyna różnica, polega na tym, iż funkcje bazowe używane w klasycznej metodzie elementów skończonych są wielomianami stopnia p o ciągłości we wnętrzu elementów, natomiast na granicy elementów skończonych są one klasy . Izogeometryczna metoda elementów skończonych uogólnia funkcje bazowe na wielomiany stopnia p które mogą być klasy na całym obszarze obliczeniowym. Mogą one być również klasy tylko we wnętrzach elementów oraz klasy na granicy elementów. W szczególności funkcje B-spline używane w izogeometrycznej metodzie elementów skończonych definiowane są przez tzw. wektory węzłów. Poprzez powtórzenie węzłów na granicy elementów uzyskuje się funkcje B-spline równoważne klasycznym wielomianom Lagrange'a.

Izogeometryczna metoda elementów skończonych stosowana jest zazwyczaj na siatkach będących obrazem regularnych (kwadratowych lub sześciennych) grup elementów, natomiast klasyczna metoda elementów skończonych może używać elementów kwadratowych lub trójkątnych w 2D, oraz sześciennych, czworościennych, pryzm i piramid w 3D. Istnieją natomiast nowoczesne metody definiowania funkcji B-spline na elementach trójkątnych i czworościennych, i wówczas ta równoważność (fakt iż izogeometryczna metoda elementów skończonych zwiększa ciągłość funkcji bazowych) jest zachowana.

Klasyczna metoda elementów skończonych aproksymuje pola skalarne i wektorowe występujące w obliczeniach inżynierskich w sposób kawałkami ciągły, a izogeometryczna metoda elementów skończonych w sposób globalnie ciągły. Istnieją oczywiście problemyobliczeniowe dla których metoda izogeometryczna daje lepsze przybliżenie, oraz problemy obliczeniowe dla których klaszyczna metoda elementów skończonych daje lepsze przybliżenia.

Jakie elementy w moim przekonaniu powinien zawierać podręcznik o klasycznej metodzie elementów skończonych? 1. Wprowadzenie definicji elementu skończonego i klasycznych funkcji bazowych, takich jak wielomiany Lagrange'a oraz

hierarchiczne wielomiany stosowane na przykład w adaptacyjnej metodzie elementów skończonych. Definicje te powinny obejmować przynajmniej elementy prostokątne i trójkątne w dwóch wymiarach.

2. Wprowadzenie algorytmów generacji siatek obliczeniowych, w szczególności zbudowanych z trójkątów i czworościanów, oraz algorytmów adaptacji siatek obliczeniowych

3. Przedstawienie szeregu przykładowych problemów prostych w formie silnej i w formie słabej

4. Przedstawienie algorytmów generacji układów równań, macierzy lewej strony (w przypadku niektórych problemów nazywanej macierzą sztywności) i wektora prawej strony

5. Przedstawienie algorytmów solwerów stosowanych do rozwiązywania układów równań 6. Przedstawienie przykładowych problemów obliczeniowych z wynikami

7. Przedstawienie metod stabilizacji dla problemów trudnych obliczeniowo, np. metody Discountinuous Galerkin (DG) lub metody Streamline Upwind Petrov-Galerkin (SUPG)

Ad.1) Definicje formalne klasycznej metody elementów skończonych opisane zostały w modułach rozdziału "Matematyczne sformułowanie metody elementów skończonych".

Książka zawiera również szereg nieformalnych definicj. W szczególności elementy trójkątne opisane zostały w rozdziale "Siatki nieregularne"; wielomiany Lagrange'a na elementach prostokątnych i sześciennych zdefiniowane zostały poprzez powtórzenie węzłów w wektorze węzłów definiujących funkcje bazowe B-spline (pamiętając że wielomany Lagrange'a zawierają się w funkcjach B-spline) w rozdziale "Dyskretyzacja za pomocą różnych funkcji bazowych"

C

k

hp

C

p−1

_C

0

C

k

Ad.2) Algorytmy generacji siatek są obszernie opisane w rozdziale "Przetwarzanie siatek obliczeniowych",

Ad.3) Formy słabe i formy silne nie zależą od sposobu dyskretyzacji. W rozdziale "Sformułowania wariacyjne dla różnych problemów i metod" podanych jest szereg sformułowań wariacyjnych niezależnych od tego czy używamy metody klasycznej czy izogeometrycznej. Mamy w szczególności równania transportu ciepła, równania konwekcji-dyfuzji, problem Stokesa, oraz równania problemu liniowej sprężystości.

Rozdziały te zawierają również dyskretyzację zazwyczaj wykonaną z pomocą izogeometrycznej metody elementów skończonych, jednakże w części ogólnej dotyczącej sformułowań silnych i wariacyjnych są one niezależne od metody dyskretyzacji.

Ad.4) Zagadnienie generacji układów równań wynikających z dyskretyzacji klasyczną metodą elementów skończonych zostało zilustrowane w rozdziale "Transport ciepła za pomocą tradycyjnej metody elementów skończonych" dla przypadku

dwuwymiarowego. Odpowiednie algorytmy dla klasycznej metody elementów skończonych umieszczono w rozdziale "Formalne matematyczne sformułowanie metody elementów skończonych". Umieszczono tam również przykład jednowymiarowej klasycznej metody elementów skończonych.

Ad.5) Algorytmy solwerów opisane są w rozdziale "Solwery układów równań liniowych generowanych podczas obliczeń MES", w modułach "Algorytm eliminacji Gaussa", "Algorytm eliminacji Gaussa z pivotingiem", "Algorytm LU faktoryzacji", "Algorytm solwera frontalnego", "Algorytm solwera wielo-frontalnego", "Algorytm solwera zmienno-kierunkowego", "Preconditioner". Ad.6) W rozdziale "Sformułowania wariacyjne dla różnych problemów i metod", w module "Transport ciepła za pomocą tradycyjnej metody elementów skończonych" podany jest przykład sformułowania słabego i silnego dla dwuwymiarowego problemu transportu ciepła z wykorzystaniem klasycznej metody elementów skończonych, oraz szereg algorytmów dotyczących generacji układu równań. W rozdziale "Formalne matematyczne sformułowanie metody elementów skończonych" umieszczono przykład jednowymiarowej klasycznej metody elementów skończonych, oraz szereg przydatnych algorytmów.

Ad.7) Metoda stabilizacji DG zostala opisana w rozdziale "Metody Stabilizacji" w module "Stabilizacja równań Stokesa za za pomocą metody Discontinuous Galerkin (DG)". W module "Stabilizacja równań adwekcji-dyfuzji" opisano metodę Streamline Upwind Petrov-Galerkin (SUPG) która działa zarówno dla klasycznej jak i izogeometrycznej metody metody elementów skończonych

Jakie elementy w moim przekonaniu powinien zawierać podręcznik o izogemetrycznej metodzie elementów skończonych? 1. Wprowadzenie funkcji bazowych B-spline definiowanych na grupie (patchu) elementów. Definicje te powinny obejmować

sposób definicji funkcji za pomocą wektora węzłów

2. Wprowadzenie do algorytmów mapowania obiektów geometrycznych przez patche elementów w systemach CAD, mapowania patchów elementów na obiekty geometryczne, oraz algorytmów adaptacji patchów elementów 3. Przedstawienie szeregu przykładowych problemów prostych w formie silnej i w formie słabej

4. Przedstawienie algorytmów generacji układów równań, macierzy lewej strony (w przypadku niektórych problemów nazywanej macierzą sztywności) i wektora prawej strony

5. Przedstawienie algorytmów solwerów stosowanych do rozwiązywania układów równań 6. Przedstawienie przykładowych problemów obliczeniowych z wynikami

7. Przedstawienie metod stabilizacji dla problemów trudnych obliczeniowo, np. metody minimalizacji reziduum, metody SUPG Ad.1) Ten apekt został szczegółowo opisany w rozdziale "Dyskretyzacja za pomocą różnych funkcji bazowych", moduły "Liniowe funkcje bazowe", "Funkcje bazowe wyższego stopnia rzędu Ck w 1D", "Ulepszona analiza izogeometryczna w 1D", "Uogólnienie funkcji bazowych poprzez iloczyn tensorowy na 2D", "Uogólnienie funkcji bazowych poprzez iloczyn tensorowy na 3D" Ad.2) Aspekt obliczeń adaptacyjnych w metodzie izogeometrycznej jest pokrótce opisany w rozdziale "Przetwarzanie siatek obliczeniowych" moduł "Analiza izogeometryczna na siatkach adaptacyjnych". Aspekt mapowania obiektów CAD na grupy elementów został w podręczniku pominięty ze względu na swoją obszerność i przynależność do pokrewnej (ale innej) tematyki związanej z modelowaniem geometrii w systemach informatycznych.

Ad.3) Zagadnienie to zilustrowane zostało w rozdziale "Przykładowy problem dwuwymiarowej projekcji bitmapy" moduły "Aproksymacja za pomocą funkcji bazowych B-spline", "Wyprowadzenie układu równań liniowych", "Wygenerowanie układu równań linowych za pomocą obliczeń analitycznych", "Rozwiązanie układu równań linowych", "Interpretacja rozwiązania". Ad.4) Algorytmy te zostały opisane w rozdziale "Solwery układów równań liniowych generowanych podczas obliczeń MES", moduły "Algorytm eliminacji Gaussa", "Algorytm eliminacji Gaussa z pivotingiem", "Algorytm LU faktoryzacji", "Algorytm solwera frontalnego", "Algorytm solwera wielo-frontalnego", "Algorytm solwera zmienno-kierunkowego", "Preconditioner". Wszystkie te algorytmy jako takie są niezależne od faktu czy używamy klasycznej czy izogeometrycznej metody elementów skończonych. Dodatkowo moduły "Algorytm solwera iteracyjnego" oraz "Wybór solwera w zależności od rodzaju problemu" dotyczą przypadku izogeometrycznej metody elementów skończonych.

Ad.5) Algorytmy solwerów opisane są w rozdziale "Solwery układów równań liniowych generowanych podczas obliczeń MES", w modułach "Algorytm eliminacji Gaussa", "Algorytm eliminacji Gaussa z pivotingiem", "Algorytm LU faktoryzacji", "Algorytm solwera frontalnego", "Algorytm solwera wielo-frontalnego", "Algorytm solwera zmienno-kierunkowego", "Preconditioner". Ad.6) W rozdziale "Przykładowy problem dwuwymiarowej projekcji bitmapy" i "Sformułowania wariacyjne dla różnych problemów i metod" znajdują się obszerne przyklady obliczeniowe dla izogeometrycznej metody elementów skończonych. Ad.7) Metoda stabilizacji izogeometrycznej metody elementów skończonych zostala opisana w rozdziale "Metody Stabilizacji" w modułach "Stabilizacja równań Stokesa za za pomocą metody minimalizacji reziduum" , oraz "Stabilizacja równań adwekcji-dyfuzji za pomocą metody Streamline Upwind Petrov-Galerkin (SUPG)".

Dodatkowo podręcznik zawiera rozdział opisujący rozszerzenie metody elementów skończonych na problemy niestacjonarne (modelujące stan systemów zmieniający się w czasie) oraz wspomniany wcześniej rozdział wprowadzający do matematycznych podstaw metody elementów skończonych.

Wszelkie uwagi oraz pytania dotyczące treści książki proszę kierować na adres maciej.paszynski@agh.edu.pl

Rozdział 1. Wstęp do metody elementów

Rozdział 1. Wstęp do metody elementów

skończonych

skończonych

Przykładowy problem dwuwymiarowej projekcji

Przykładowy problem dwuwymiarowej projekcji

bitmapy

bitmapy

W rozdziale tym zajmiemy się przykładowym problemem projekcji, który posłuży nam do zbudowania intuicji leżącej u podstaw metody elementów skończonych.

PRZYKŁAD

Przykład 1: Problem projekcji bitmapy

Przykład 1: Problem projekcji bitmapy

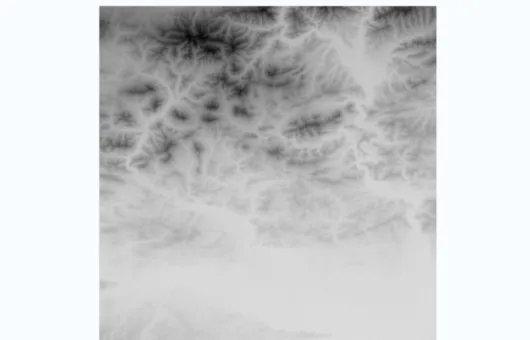
Wyobraźmy sobie że dostaliśmy dwuwymiarową bitmapę taką jak na Rys. 1. Bitmapa ta reprezentuję zdjęcie satelitarne ukształtowania terenu. Bitmapa jest monochromatyczna, każdy piksel bitmapy posiada wartość całkowitą w zakresie od 0 do 255. Wartość piksela równa 0, reprezentowana na rysunku przez czarne piksele, oznacza fragmenty terenu których średnia wysokość jest najwyższa. Są to miejsca położone na szczytach gór. Z koleji wartość piksela równa 255, reprezentowana na rysunku przez piksele w kolorze białym, oznaczają fragmenty terenu których średnia wysokość jest najniższa. Są to miejsca położone w dolinach gór.

Rysunek 1: Dwuwymiarowa bitmapa reprezentująca ukształtowanie terenu. Intensywność każdego piksela waha się pomiędzy wartościami 0 a 255. Wartość 0 (kolor czarny) teren o najwyższej wysokości (szczyt góry), wartość 255 (kolor biały) oznacza teren o najniższej wysokości (najniższy punkt w dolinie).

Przyglądnijmy się teraz jak wygląda reprezentacja komputerowa terenu opisana taką bitmapą. Nasz teren podzielony został na obszary kwadratowe reprezentowane przez poszczególne piksele. Jedyna informacja jaką mamy dla każdego takiego fragmentu terenu, to jego średnia wysokość odpowiadająca wysokości reprezentowanej przez intensywność piksela. Gdyby rzeczywistość wyglądała tak jak na naszej bitmapie, wówczas musieli byśmy skakać z jednej kwadratowej płaskiej platformy na drugą kwadratową płaską platformę, a ich wysokości zmieniały by się od 0 do 255, w pewnych jednostkach wynikających z różnicy pomiędzy minimalnym i maksymalnym ukształtowaniem terenu.

Rysunek 2: Ciągła aproksymacja terenu na podstawie bitmapy przedstawiającej mapę ukształtowania terenu. Teraz, dla lepszej ilustracji, najwyższe fragmenty terenu zaznaczone zostały kolorem czerwonym, a najniższe fragmenty terenu zaznaczone zostały kolorem ciemnoniebieskim.

Wyobraźmy sobie teraz że chcemy uciąglić naszą komputerowa reprezentacje terenu. Chcemy żeby wysokości zmieniały się w sposób ciągły, tak jakby nasz wszechświat odlany był ze smukłego plastiku. Oczywiście taka reprezentacja terenu będzie bardziej zbliżona do rzeczywistości, ale nadal będzie jedynie jej przybliżeniem. Chcemy dokonać "plastikowego" odlewu naszego terenu tak jak przedstawiono to na Rys. 2. Nasz model nie jest już bitmapą zawierającą płaskie piksele, jest natomiast smukłym plastikowym odlewem rzeczywistości po którym można ześlizgiwać się z jednego miejsca na inne.

Aproksymacja za pomocą funkcji bazowych B-spline

Aproksymacja za pomocą funkcji bazowych B-spline

Żeby napisać program komputerowy obliczający takie ciągłe przybliżanie terenu, musimy wykonać następujące czynności. Po pierwsze, musimy opisać nasz problem w sposób formalny, matematyczny. W szczególności musimy wybrać matematyczną definicję obiektu - bitmapy, oraz matematyczną definicje naszego ciągłego opisu terenu reprezentowanego przez bitmapę. Rozsądnym rozwiązaniem wydaje się powiedzenie iż bitmapa jest funkcją określoną na obszarze

gdzie poprzez oznaczamy cały obszar na którym rozpięta jest nasza bitmapa.

Z koleji nasza ciągła reprezentacja świata będzie reprezentowana przez funkcję o wartościach rzeczywistych.

Chcemy by nasza funkcja była "smukła" i ciągła. Matematycznie zapisujemy warunek że nasza funkcja będzie klasy , oznacza to że w każdym punkcie będzie na tyle smukła żeby dało się policzyć jej pochodne w kierunkach prostopadłych do brzegów naszego obszaru. Oznacza to praktycznie iż w każdym punkcie możemy do wykresu naszej funkcji przyłożyć "linijkę" prostopadle do jednego z brzegów naszego obszaru, i zmierzyć kąt pomiędzy tą linijką a podstawą (powierzchnią płaską rozpostartą na wysokości zerowej). Pochodna to przecież nic innego jak tangens tego kąta. Innymi słowy nasza funkcja nie będzie miała "załamań" ani przerw, na których nie byłoby wiadomo jak przykładać naszą linijkę. Na załamaniach linijka ta przeskakiwała by z jednej pozycji na drugą, a w przypadku dziury w ogóle nie byłoby wiadomo jak ją przyłożyć. Oczywiście możliwość mierzenia pochodnej (przykładania linijki) w dwóch kierunkach prostopadłych do brzegu obszaru oznacza również możliwość przykładania linijki i mierzenia pochodnych kierunkowych w dowolnych innych kierunkach nie prostopadłych do brzegu. Możemy więc gładko przemieszczać się po powierzchni wykresu takiej smukłej funkcji, w dowolnych kierunkach.

Jak uzyskać taką ciągłą smukłą funkcję? Musimy zdecydować jak nasza funkcja zostanie skonstruowana. Na przykład, możemy obszar na którym rozpięta jest bitmapa podzielić na pewne elementy, i na tych elementach zdefiniować zbiór wielu smukłych funkcji, z których następnie "skleimy" naszą funkcję .

Wyobraźmy sobie że na wysokości odpowiadającej wysokości zerowej (takiej której odpowiada wartość piksela zero) budujemy płaską dwuwymiarową siatkę, której liczba kwadratowych elementów jest dowolna. Oczka te zgodnie z przyjętą nomenklaturą nazwiemy elementami skończonymi, ponieważ każdy z tych elementów posiada ograniczony skończony obszar. Elementów tych może być mniej niż pikseli w bitmapie, i wtedy nad każdym takim elementem rozpiętych będzie kilka pikseli. Granice pomiędzy naszymi elementami nie muszą zgadzać się z granicami pikseli. Mogą one być dowolnie zdefiniowane na płaskiej powierzchni. Może również być tak, że naszych elementów jest więcej niż pikseli, i wtedy w każdym pikselu znajdować się będzie wiele takich elementów. Załóżmy jednak że naszych elementów jest mniej niż pikseli. Tworzą one regularną siatkę o elementach skończonych.

Teraz, na każdym takim elemencie definiujemy smukłą funkcję. Możemy w tym celu posłużyć się funkcjami B-spline. Funkcje te zostały po raz pierwszy wprowadzone przez amerykańskiego matematyka rumuńskiego pochodzenia Isaaka Jakuba Schoenberga [9].

Funkcje B-spline są powszechnie stosowane w modelowaniu i symulacjiach komputerowych dzięki rosnącej popularności dziedziny zwanej analizą izogeometryczną rozpowszechnianej przez prof. T.J.R. Hughesa.[5].

Ideą tych metod jest zastosowanie rodzin funkcji B-spline do obliczeń za pomocą metody elementów skończonych.

Funkcje te oznaczamy , gdzie oraz oznaczają numeracje naszych funkcji, a 2 oznacza iż są to wielomiany kawałkami drugiego stopnia, klasy .

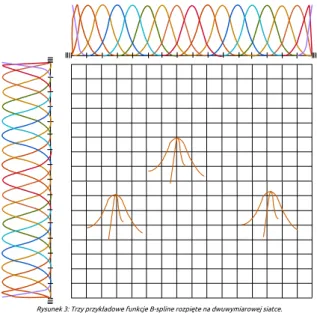
Rysunek 3: Trzy przykładowe funkcje B-spline rozpięte na dwuwymiarowej siatce.

Rys. 3 przedstawia trzy przykładowe dwuwymiarowe funkcje B-spline rozpięte na dwuwymiarowej siatce. Każda taka dwuwymiarowa funkcja spline powstaje poprzez wybranie i przemnożenie przez siebie dwóch jednowymiarowych funkcji B-spline, jednej wybranej ze zbioru jednowymiarowych funkcji B-spline rozpiętych wzdłuż poziomego brzegu siatki, i drugiej wybranej ze zbioru jednowymiarowych funkcji B-spline rozpiętych wzdłuż pionowego brzegu siatki. Zbiory te nazywamy bazami jednowymiarowych funkcji B-spline.

Te jednowymiarowe funkcje B-spline oznaczamy z koleji oraz gdzie zmienne oraz identyfikują kierunki (osie układu współrzędnych) wzdłuż których określone są nasze B-spline'y (oś pozioma oraz oś pionowa ), oraz oznaczają numeracje tych funkcji (którą kolejną jednowymiarową funkcję B-spline wybieramy z takiej jednowymiarowej bazy), oraz 2 oznacza ponownie że są to wielomiany kawałkami drugiego stopnia, klasy (czyli że umiemy z nich liczyć pierwsze pochodne). Następnie wybrane funkcje jednowymiarowe są przemnażane przez siebie, co daje nam smukłą dwumymiarową funkcję B-spline. Taką metodę tworzenia dwuwymiarowych funkcji przez przemnażanie stosownych jednowymiarowych funkcji nazywa się iloczynem tensorowym funkcji.

Jest to zilustrowane na . Uzyskane w ten sposób dwuwymiarowe funkcje B-spline mają kształt smukłego "pagórka", określonego na dziewięciu sąsiadujących elementach. Najwyższy punkt takiej funkcji - pagórka znajduje się w centrum środkowego elementu.

Ω = [1, maxx] × [1, maxy] ∋ (x, y) → BITMAP(x, y) ∈ [0, 255]

Ω

u

Ω = [1, maxx] × [1, maxy] ∋ (x, y) → u(x, y) ∈ [0, 255]

C

1

u

∗

Nx

Ny

(x, y)

Bi,j;2

i

j

C

1

(x)

B

x i;2

B

yj;2

(y)

x

y

x

y i

j

C

1

(x, y) =

(x)

(y)

Bi,j;2

B

x i;2

B

yj;2

Funkcje te schodzą gładko do wartości zerowej, przyjmowanej na brzegach kwadratu zdefiniowanego przez dziewięć elementów na których funkcja ta jest określona. Funkcje te zgodnie z przyjętą nomenklaturą nazwiemy funkcjami bazowymi.

Rysunek 4: Dwuwymiarowa funkcja B-spline sklejona za pomocą dwóch jednowymiarowych funkcji B-spline.

Naszą ciągłą aproksymacje terenu uzyskamy w ten sposób, że zsumujemy ze sobą wiele takich smukłych pagórków - B-spline'ów. Każdy z nich zostanie przeskalowany (podniesiony do góry lub dół) tak by w sumie otrzymać ciągłą aproksymację terenu. Jeśli poprawnie dobierzemy wysokości poszczególnych pagórków, dostaniemy wówczas smukłe przybliżenia naszego terenu tak jak przedstawiono to na Rys. 2.

Powstaje teraz pytanie, w jaki sposób dobrać wysokości do których wyciągniemy nasze funkcje bazowe. Pierwsza metoda która przychodzi nam do głowy to wybrać wartość piksela z znajdującego się dokładnie w najwyższym punkcie B-spline (na środku pagórka). Niestety metoda ta ma kilka wad. Po pierwsze, jeśli naszych funkcji bazowych B-B-spline jest mniej niż pikseli, to wówczas ignorujemy wszystkie sąsiednie piksele znajdujące się w obszarze naszego B-spline'a, wybierając jedynie jedną wartość ze środka obszaru. Możliwe że nasza bitmapa posiada pewne zaburzenia i że trafimy akurat na lokalny odskok będący błędem pomiaru, lub że trafimy akurat w lokalną dziurę w ukształtowaniu terenu, lub w lokalne drzewo lub budynek który akurat zakłócił pomiar ukształtowania terenu. Po drugie, zauważmy że nasze funkcje bazowe rozpościerają się na kwadracie dziewięciu elementów. Skoro każdą taką funkcję B-spline skojarzyć można ze środkiem swojego elementu, oraz każda z tych funkcji rozpościera się na dziewięć sąsiednich elementów, oznacza to iż na każdym elemencie rozpostartych jest w sumie dziewięć takich funkcji, oraz że sąsiadujące funkcje zachodzą na siebie. Jeśli więc rozciągalibyśmy funkcje tak aby ich punkt maksymalny pokrywał się z centralnym pikselem, oraz zsumowalibyśmy te wszystkie funkcje razem w celu uzyskania naszej globalnej funkcji , to wówczas na każdym elemencie, nawet w punkcie centralnym, nasza wynikowa aproksymacja (suma tych funkcji) byłaby wyżej niż nasz centralny piksel, dlatego iż sąsiednie osiem funkcji również byłyby niezerowe na danym elemencie i podnosiłyby one wartość naszej aproksymacji w tym punkcie do góry.

Wyprowadzenie układu równań liniowych

Wyprowadzenie układu równań liniowych

Problem doboru współczynników kombinacji liniowej funkcji B-spline służących do aproksymacji bitmapy (problem skalowania poszczególnych B-spline'ów) jest problemem globalnym, i należy rozwiązać go biorąc pod uwagę wszystkie współczynniki równocześnie.

W tym celu przeprowadzamy następujące rozumowanie, które jest podstawą intuicji leżących u podstaw metody elementów skończonych.

Wyprowadzenie 1: Wyprowadzenie układu równań liniowych dla problemu

Wyprowadzenie 1: Wyprowadzenie układu równań liniowych dla problemu

izogeometrycznej projekcji

izogeometrycznej projekcji

Celem naszym jest wykonanie aproksymacji bitmapy za pomocą smukłej funkcji Nasza smukła funkcja powstaje poprzez kombinację liniową wielu funkcji bazowych

gdzie to współczynniki tej kombinacji, których wartości musimy policzyć. Nasze funkcje bazowe rozpięte są na elementach siatki. Funkcji tych jest więc również , i w związku z powyższym musimy obliczyć współczynników . Każdy z tych współczynników mówi mi jak przeskalować jedną

funkcję bazową, dwuwymiarową funkcję B-spline .

W jaki sposób obliczyć te współczynniki .

Zamiast wybierać wartości pikseli, użyjemy metody uśredniania. Do uśredniania zastosujemy również nasze funkcje bazowe

B-spline. Chcemy aby nasza aproksymacja przybliżała bitmapę .

Wybierzmy więc dowolnie jedną funkcję B-spline

. Wybraliśmy funkcję o indeksach . Dla uproszczenia nazwialiśmy ją .

Trzy przykładowe wybory naszej funkcji B-spline zilustrowane są na rysunku Rys. 3. Funkcję tą nazwiemy funkcją testującą. Jest to standardowa nomenklatura używana w metodzie elementów skończonych.

Następnie użyjemy naszej funkcji testującej w celu obliczenia średniej z bitmapy w otoczeniu tej funkcji.

Innymi słowy chcemy żeby nasza aproksymacja przybliżała naszą bitmapę z takim rozkładem uśredniania jaki daje nam nasza funkcja testująca. Żeby zapisać tą operację matematycznie, przemnożymy nasze równania aproksymacji przez funkcję testującą i policzymy całkę

.

Największy wpływ na wartość tej średniej, zgodnie z wyglądem funkcji bazowej B-spline, ma punkt centralny, a punkty coraz bardziej oddalone mają coraz mniejszy wpływ na wartość średniej.

Zauważmy teraz że jeden wybór funkcji testującej daje nam jedno równanie.

Na ile sposobów możemy wybrać nasze funkcje testujące? Skoro każda z nich jest B-spline'm skojarzonym z centrum elementu, a elementów jest oznacza to że możemy wybrać funkcji testujących.

BITMAP(x, y)

u

u

u(x, y)

≈ BITMAP(x, y)

u

u(x, y) =

∑

Nx,Ny

(x) (y)

i=1,j=1

ui,j

B

xi

B

yj

u(x, y)

=

j

(y)

∗

Nx

Ny

Nx

∗

Ny

∗

Nx

Ny

ui,j

ui,j

(x, y) =

(x) (y)

Bi,j;2

B

x i

B

yj

{ }i = 1, . . ,

ui,j

Nx

; j = 1, . . . ,

Ny

u(x, y) ≈ BITMAP(x, y)

v(x, y) =

Bk,l;2

(x, y) =

B

x k

B

yl

k, l

v

u

u(x, y)v(x, y) =

BITMAP(x, y)v(x, y)

∫

Ω

∫

Ω

v

∗

Każdy z takich wyborów funkcji testujących daje nam jedno równanie, dostajemy więc układ równań

Pytanie które należy teraz zadać, to kwestia niewiadomych w naszym układzie równań. Mamy równań, ale gdzie znajdują się niewiadome? Czym są niewiadome w naszym układzie równań? Żeby dotrzeć do niewiadomych, należy przypomnieć sobie jak skonstruowana została nasza funkcja aproksymująca bitmapę.

Nasze niewiadome to współczynniki

określające w jaki sposób "wyciągamy" poszczególne B-spline "pagórki" w celu uzyskania jak najlepszej aproksymacji bitmapy. Wstawiamy więc naszą kombinację liniową funkcji B-spline w miejsce in dostajemy

Korzystamy teraz z algebraicznej właściwości układu równań, która to pozwala nam wyciągnąć sumę wraz ze współczynnikami przed poszczególne całki

Zauważmy teraz iż powyższy układ równań można zapisać w postaci macierzowej.

W szczególnoci zaznaczone w kolorze czerwonym współczynniki tworzą wektor niewiadomych, całki

tworzą macierz, której wiersze numerowane są od , a kolumny

od . Jest tak ponieważ całki zawierają iloczyny dwóch dwuwymiarowych funkcji B-spline, dwóch

"pagórków" rozpiętych na siatce elementów skończonych. Pierwsza funkcja B-spline, zaznaczona kolorem czarnym, używana jest do aproksymacji, natomiast druga funkcja B-spline, zaznaczona kolorem niebieskim, używana jest do próbkowania bitmapy (do liczenia średniej z bitmapy). Wektorem prawej strony jest wektor całek w których to bitmapa jest przemnażana przez

"niebieskiego" B-spline'a testującego używanego do uśredniania, i odcałkowywana zgodnie z rozkładem opisanym przez naszego testującego B-spline'a.

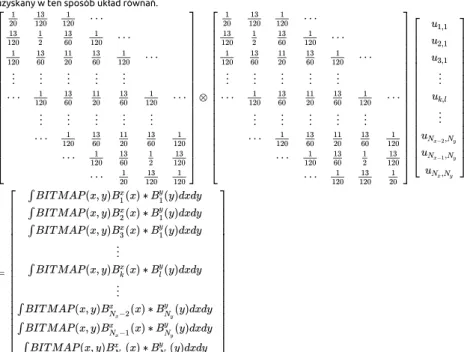
Podsumowując, uzyskaliśmy w ten sposób następujący układ równań, w którym niewiadome to współczynniki

W "magiczny" sposób rozwiązanie powyższego układu równań da nam najlepsze współczynniki przybliżenia bitmapy poprzez nasze B-spline'y.

Wspomniana "magia" wynika tutaj ze sposobu określania poszczególnych równań naszego układu, w którym to postulowaliśmy iż średnio, w sensie rozkładu określonego funkcjami testującymi B-spline, nasza aproksymacja odpowiadać będzie bitmapie.

Wygenerowanie układu równań linowych za pomocą

Wygenerowanie układu równań linowych za pomocą

obliczeń analitycznych

obliczeń analitycznych

Następny etap to wygenerowanie układu równań liniowych oraz jego rozwiązanie.

Oczywiście zależy nam na tym żeby wybrane algorytmy generacji oraz rozwiązywania układów równań były najszybsze możliwe.

∗

Nx

Ny

∫ u(x, y)

B

x

(x) (y)

= ∫ BITMAP(x, y)

(x) (y)

1

B

y1

B

x1

B

y1

∫ u(x, y)

B

x

(x) (y)

= ∫ BITMAP(x, y)

(x) (y)

1

B

y2

B

x1

B

y2

⋮

∫ u(x, y)

B

x

(x) (y)

= ∫ BITMAP(x, y)

(x) (y)

k

B

yl

B

xk

B

yl

⋮

∫ u(x, y)

B

x

(x)

(y)

= ∫ BITMAP(x, y)

(x)

(y)

Nx

B

y −1 Ny

B

xNx

B

y −1 Ny

∫ u(x, y)

B

x

(x)

(y)

= ∫ BITMAP(x, y)

(x)

(y)

.

Nx

B

y Ny

B

x Nx

B

y Ny

∗

Nx

Ny

u

u(x, y) ≈

∑

_i,j

u

i,j

B

xi

(x) (y)

B

yj

{ }i = 1, . . . ,

ui,j

Nx

, j = 1, . . . ,

Ny

u

∫

∑

i,j

u

i,j

B

ix

(x) (y)

B

jy

B

x1

(x) ∗ (y)

B

y1

= ∫ BITMAP(x, y)

B

x1

(x) ∗ (y)

B

y1

∫

∑

_i,j

u

i,j

B

ix

(x) (y)

B

jy

B

x1

(x) ∗ (y)

B

y2

= ∫ BITMAP(x, y)

B

x1

(x) ∗ (y)

B

y2

⋮

∫

∑

i,j

u

i,j

B

ix

(x) (y)

B

jy

B

xk

(x) ∗ (y)

B

yl

= ∫ BITMAP(x, y)

B

xk

(x) ∗ (y)

B

yl

⋮

∫

∑

_i,j

u

i,j

B

xi

(x) (y)

B

yj

B

xNx

(x) ∗

B

(y)

= ∫ BITMAP(x, y)

(x) ∗

(y)

y −1 Ny

B

x Nx

B

y −1 Ny

∫

∑

_i,j

u

i,j

B

xi

(x) (y)

B

yj

B

xNx

(x) ∗

B

(y)

= ∫ BITMAP(x, y)

(x) ∗

(y)

y Ny

B

x Nx

B

y Ny

∫

(x) (y)

(x) ∗ (y)

= ∫ BITMAP(x, y)

(x) ∗ (y)

∑

i,j

u

i,j

B

xi

B

yj

B

x1

B

y1

B

x1

B

y1

∫

(x) (y)

(x) ∗ (y)

= ∫ BITMAP(x, y)

(x) ∗ (y)

∑

i,j

u

i,j

B

xi

B

yj

B

x1

B

y2

B

x1

B

y2

⋮

∫

(x) (y)

(x) ∗ (y)

= ∫ BITMAP(x, y)

(x) ∗ (y)

∑

i,j

u

i,j

B

xi

B

yj

B

xk

B

yl

B

xk

B

yl

⋮

∫

(x) (y)

(x) ∗

(y)

= ∫ BITMAP(x, y)

(x) ∗

(y)

∑

_i,j

u

i,j

B

xi

B

yj

B

xNx

B

y −1 Ny

B

x Nx

B

y −1 Ny

∫

(x) (y)

(x) ∗

(y)

= ∫ BITMAP(x, y)

(x) ∗

(y)

∑

i,j

u

i,j

B

xi

B

yj

B

xNx

B

y Ny

B

x Nx

B

y Ny

, j

u

i

∫

B

x

(x) (y)

(x) ∗ (y)dx

i

B

yj

B

xk

B

yl

i = 1, . . . ,

Nx

; j = 1, . . . ,

Ny

k = 1, . . . ,

Nx

; l = 1, . . . ,

Ny

{ }i = 1, . . . ,

u

i,j

N

x

; j = 1, . . .

N

y

⎡

⎣

⎢⎢

⎢⎢

⎢⎢

∫

B

x 1,p

B

y1,p

B

x1,p

B

y1,p

∫

B

x 2,p

B

y1,p

B

x1,p

B

y1,p

⋮

∫

B

x ,p Nx

B

y ,p Ny

B

x1,p

B

y 1,p

∫

B

x 1,p

B

y1,p

B

x2,p

B

y1,p

∫

B

x 2,p

B

y1,p

B

x2,p

B

y1,p

⋮

∫

B

x ,p Nx

B

y ,p Ny

B

x2,p

B

y 1,p

⋯

⋯

⋮

⋯

∫

B

x 1,p

B

y1,p

B

xNx,p

B

y ,p Ny

∫

B

x 2,p

B

y1,p

B

xNx,p

B

y ,p Ny

⋮

∫

B

x ,p Nx

B

y ,p Ny

B

xNx,p

B

y ,p Ny

⎤

⎦

⎥⎥

⎥⎥

⎥⎥

⎡

⎣

⎢⎢

⎢⎢

u

1,1

u

2,1

⋮

u

Nx,Ny

⎤

⎦

⎥⎥

⎥⎥

=

⎡

⎣

⎢⎢

⎢⎢

⎢

∫ BITMAP(x, y)

B

x

(x) ∗ (y)dx

1

B

y1

∫ BITMAP(x, y)

B

x

(x) ∗ (y)dx

1

B

y2

⋮

∫ BITMAP(x, y)

B

x

(x) ∗

(y)dx

Nx

B

y Ny

⎤

⎦

⎥⎥

⎥⎥

⎥

W pierwszej kolejności generujemy macierz zawierającą całki z iloczynów dwuwymiarowych funkcji B-spline.

Możemy dla uproszczenia przyjąć że wektory węzłów są równoodległe, oraz że jednostką odległości wzdłuż danej osi układu współrzędnych jest odległość pomiędzy dwoam węzłami w wektorze węzłów.

Zauważmy najpierw że

Innymi słowy dzięki temu że nasze dwuwymiarowe B-spline'y powstają poprzez przemnożenie jednowymiarowych B-spline'ów, możemy rozdzialić nasze dwuwymiarowe całki na iloczyn dwóch jednowymiarowych całek, w których przemnażamy i całkujemy pary jednowymiarowych B-spline'ów.

Musimy więc wygenerować następującą macierz

Zauważmy że macierz ta ma następującą strukturę. W wierszach zmieniają się pierwsze B-spline'y w obu całkach pojedynczych (całce po $x$ i całce po $y$). Wiersze zmieniają się tak, że najpierw mamy kolejno B-spline'y

dla ustalonego . Następnie powtarzamy wszystkie dla ustalonego , i tak

dalej, występują bloki wszystkich kolejnych B-spline'ów względem dla kolejnych ustalonych B-spline'ów aż do ostatniego

bloku w którym występują kolejno dla ustalonego ostatniego

W kolumnach sytuacja jest podobna, dotyczy ona natomiast drugich B-spline'ów w każdej całce pojedynczej. Kolumny zmieniają

się więc tak, że najpierw mamy kolejno B-spline'y dla ustalonego . Następnie powtarzamy wszystkie

dla ustalonego , i tak dalej, występują bloki wszystkich kolejnych B-spline'ów względem dla kolejnych ustalonych B-spline'ów aż do ostatniego bloku w którym występują kolejno dla ustalonego ostatniego

Macierz która ma taką strukturę jest iloczynem Kroneckera dwóch mniejszych macierzy, jednej w której występują same wyrazy z pierwszych całek pojedynczych (pary B-spline'ów względem ),

i drugiej w której występują same wyrazy z drugich całek pojedynczych (pary B-spline'ów względem ). Matematyczny zapis takiego iloczynu Kroneckera to symbol pomiędzy dwoma wspomnianymi macierzami. Symbol "=" z przodu oznacza iż iloczyn Kroneckea tych macierzy daje naszą dużą macierz.

Zapis oznacza, iż przemnażamy przez siebie odpowiednie wyrazy dwóch macierzy tak żeby dostać oryginalną macierz .

Rysunek 5: Baza jednowymiarowych B-spline'ów.

Musimy teraz obliczyć całki z iloczynów par jednowymiarowych B-spline'ów, przedstawionych na rysunku Rys. 5.

Zauważmy najpierw że jeśli przemnożymy przez siebie dwa jednowymiarowe B-spline'y których wykresy nie nachodzą na siebie (matematycy powiedzą "które nie mają wspólnego suportu"), na przykład oraz z rysunku Rys. 5, wówczas całka Dzieje się tak dlatego ponieważ na każdym przedziale przedstawionym na rysunku Rys. 5 jeden z B-spline'ów jest równy zeru, czyli

Następnie, możemy przyjąć jako jednostkę długości średnicę elementu, wówczas każdy przedział będzie miał średnicę równą jeden.

Następnie musimy wprowadzić wzory na poszczególne segmenty B-spline'a (przedstawione na prawym panelu rysunku Rys. 5).

Segementy te oznaczamy .

Ponieważ jedynie całki z nachodzących na siebie B-spline'ów dają niezerowe wartości, nad każdym przedziałem musimy tak naprawdę obliczyć następujące całki, występujące w macierzy elementowej, w których nachodzą na siebie poszczególne segmenty B-spline'ów. Ponieważ podane wzory na segmenty obowiązują nad przedziałem 0,1, a całka nie zmienia się podczas przesunięcia (podobnie jak objętość pod stołem nie zmieni się jeśli przesuniemy stół na inne miejsce na płaskiej podłodze), możemy dla uproszczenia policzyć nasze całki właśnie w przedziale 0,1.

∫

B

x

dxdy = ∫

dx∫

dy

i,p

B

yj,p

B

xk,p

B

yl,p

B

xi,p

B

xk,p

B

yj,p

B

yl,p

⎡

⎣

⎢⎢

⎢⎢

⎢⎢

∫

B

x

dx∫

dy

1,p

B

x1,p

B

y1,p

B

y1,p

∫

B

x

dx∫

dy

2,p

B

x1,p

B

y1,p

B

y1,p

⋮

∫

B

x

dx∫

dy

,p Nx

B

x1,p

B

y ,p Ny

B

y 1,p

∫

B

x

dx∫

dy

1,p

B

x2,p

B

y1,p

B

y1,p

∫

B

x

dx∫

dy

2,p

B

x2,p

B

y1,p

B

y1,p

⋮

∫

B

x

dx∫

dy

,p Nx

B

x2,p

B

y ,p Ny

B

y 1,p

⋯

⋯

⋮

⋯

∫

B

x

dx∫

dy

1,p

B

xNx,p

B

y 1,p

B

yNy,p

∫

B

x

dx∫

dy

2,p

B

xNx,p

B

y 1,p

B

yNy,p

⋮

∫

B

x

dx∫

dy

,p Nx

B

xNx,p

B

y ,p Ny

B

y ,p Ny

⎤

⎦

⎥⎥

⎥⎥

⎥⎥

,

, . . . ,

B

x 1,p

B

x2,p

B

xNx,p

B

y 1,p

B

x1,p

,

B

x2,p

, . . . ,

B

xNx,p

B

y 2,p

x

B

y j,p

,

, . . . ,

B

x 1,p

B

x2,p

B

xNx,p

B

y ,p Ny

,

, . . . ,

B

y 1,p

B

y2,p

B

yNy,p

B

x 1,p

,

, . . . ,

B

y 1,p

B

y2,p

B

yNy,p

B

x 2,p

y

B

x i,p

B

y1,p

,

B

y2,p

, . . . ,

B

yNy,p

B

x ,p Nx

x

y

⊗

=

⊗

⎡

⎣

⎢⎢

⎢⎢⎢

⎢

∫

B

x

dx

1,p

B

x1,p

∫

B

x

dx

2,p

B

x1,p

⋮

∫

B

x

dx

,p Nx

B

x1,p

∫

B

x

dx

1,p

B

x2,p

∫

B

x

dx

2,p

B

x2,p

⋮

∫

B

x

dx

,p Nx

B

x2,p

⋯

⋯

⋮

⋯

∫

B

x

dx

1,p

B

xNx,p

∫

B

x

dx

2,p

B

xNx,p

⋮

∫

B

x

dx

,p Nx

B

xNx,p

⎤

⎦

⎥⎥

⎥⎥⎥

⎥

⎡

⎣

⎢⎢

⎢⎢

⎢⎢

∫

B

y

dy

1,p

B

y1,p

∫

B

y

dy

1,p

B

y1,p

⋮

∫

B

y

dy

,p Ny

B

y 1,p

∫

B

y

dy

1,p

B

y1,p

∫

B

y

dy

1,p

B

y1,p

⋮

∫

B

y

dy

,p Ny

B

y 1,p

⋯

⋯

⋮

⋯

∫

B

y

dy

1,p

B

yNy,p

∫

B

y

dy

1,p

B

yNy,p

⋮

∫

B

y

dy

,p Ny

B

y ,p Ny

⎤

⎦

⎥⎥

⎥⎥

⎥⎥

⊗

N

1;2

B

4;2

(x)

(x)dx = 0

∫

_{[ , ]t0t6}

B

1;2

B

4;2

(x)

(x)dx =

∫

[ , ]t0t6

B

1;2

B

4;2

(x)

(x)dx +

(x)

(x)dx +

(x)

(x)dx +

∫

_{[ , ]t0t1}

B

1;2

B

4;2

∫

[ , ]t1t2

B

1;2

B

4;2

∫

[ , ]t2t3

B

1;2

B

4;2

(x)

(x)dx +

(x)

(x)dx +

(x)

(x)dx =

∫

_{[ , ]t3t4}

B

1;2

B

4;2

∫

[ , ]t4t5

B

1;2

B

4;2

∫

[ , ]t5t6

B

1;2

B

4;2

(x) ∗ 0dx +

(x) ∗ 0dx +

(x) ∗ 0dx +

∫

[ , ]t0t1

B

1;2

∫

[ , ]t1t2

B

1;2

∫

[ , ]t2t3

B

1;2

0 ∗

(x)dx +

0 ∗

(x)dx +

0 ∗

(x)dx =

∫

_{[ , ]t3t4}

B

4;2

∫

[ , ]t4t5

B

4;2

∫

[ , ]t5t6

B

4;2

0 + 0 + 0 + 0 + 0 + 0 = 0

[ ,

ti

ti+1

]

, ,

B

1

B

2

B

3

(x) =

B

1 12

x

2

(x) = − + x +

B

2

x

2 12

(x) = (1 − x

B

3 12

)

2

[ ,

ti

ti+1

]

⎡

⎢⎢

⎢

(x) (x)dx

1 1 1 1 1

(x) (x)dx

2 1 1

(x) (x)dx

3

⎤

⎥⎥

⎥

Innymi słowy mamy tylko 9 możliwości nachodzenia na siebie poszczególnych segmentów.

Ponieważ segmenty i są symetryczne, dodatkowo mamy symetrię macierzy, czyli tak naprawdę musimy policzyć sześć całek

Z symetrii segmentów wynika również iż segment ma kształ odwróconego segmentu ,

i dlatego , innymi słowy odwrócenie funkcji nie zmienia wartości całki (podobnie jak

przekręcenie stołu o 180 stopni nie zmienia objętości znajdującej się pod stołem), oraz ,

tak naprawdę musimy więc policzyć jedynie cztery całki

Obliczamy jednowymiarowe całki z wielomianów

Uwzględniając symetrie obliczonych całek, wpisujemy je w stosowne miejsca w naszej matrycy i dostajemy

Sumując teraz wygenerowane w ten sposób kawałki macierzy dostaniemy dwie macierze tworzące nasz układ równań w postaci produktu Kroneckera macierzy.

Sumowanie przeprowadzamy w następujący sposób:

Poza wypisanymi wyrazami macierzy umieszczonymi na pięciu przekątnych, pozostałe wyrazy macierzy są równe 0. Innymi słowy naszą matrycę przesuwamy wzdłuż przekątnej od lewego górnego rogu macierzy do prawego dolnego rogu, i sumujemy nakładające się na siebie wyrazy. W ten sposób uzyskamy dwie macierze które tworzą za pomocą tak zwanego produktu Kroneckera Rys. 7 naszą macierz .

Kolejny problem do rozwiązania to policzenie całek prawej strony. Całka prawej strony to próbkowanie bitmapy przemnożonej przez poszczególne funkcje testujące (B-

spline'y używane do uśredniania bitmapy w obszarze na którym są określone).

Używamy od teraz nowej notacji, w której wprowadzamy dwuwymiarową funkcję B-spline, funkcję zmiennych , będącą

iloczynem dwóch jednowymiarowych funkcji B-spline .

Zauważmy że przemnożenie bitmapy przez B-spline'a oznacza iż całkę tą musimy policzyć jedynie po dziewięciu elementach na których określony jest B-spline .

Musimy rozwiązać teraz dwa problemy. Pierwszy problem to jaki wzór ma dziewięć fragmentów naszego B-spline'a na tych dziewięciu elementach na których jest on określony. Drugi problem, to jak policzyć całkę z bitmapy przemnożonej przez wielomian.

Zauważmy że jednowymiarowe B-spline'y składają się z trzech segmentów opisanych zgodnie z . W związku z tym, nasz dwuwymiarowy B-spline testujący na dziewięciu elementach na których jest określony składa się z odpowiednich iloczynów tych segmentów.

.

Jest to zilustrowane na rysunku Rys. 6.

⎡

⎣

⎢⎢

⎢

(x) (x)dx

∫

1 0

B

1

B

1

(x) (x)dx

∫

1 0

B

2

B

1

(x) (x)dx

∫

1 0

B

3

B

1

(x) (x)dx

∫

1 0

B

1

B

2

(x) (x)dx

∫

1 0

B

2

B

2

(x) (x)dx

∫

1 0

B

3

B

2

(x) (x)dx

∫

1 0

B

1

B

3

(x) (x)dx

∫

1 0

B

2

B

3

(x) (x)dx

∫

1 0

B

3

B

3

⎤

⎦

⎥⎥

⎥

B

1

B

3

⎡

⎣

⎢⎢

⎢

(x) (x)dx

∫

1 0

B

1

B

1

==

==

(x) (x)dx

∫

1 0

B

1

B

2

(x) (x)dx

∫

1 0

B

2

B

2

==

(x) (x)dx

∫

1 0

B

1

B

3

(x) (x)dx

∫

1 0

B

2

B

3

(x) (x)dx

∫

1 0

B

3

B

3

⎤

⎦

⎥⎥

⎥

B

3

B

1

(x) (x)dx =

(x) (x)dx

∫

1 0

B

1

B

1

∫

01

B

3

B

3

(x) (x)dx =

(x) (x)dx

∫

1 0

B

2

B

3

∫

01

B

1

B

2

⎡

⎣

⎢⎢

∫

(x) (x)dx

1 0

B

1

B

1

==

==

(x) (x)dx

∫

1 0

B

1

B

2

(x) (x)dx

∫

01

B

2

B

2

==

(x) (x)dx

∫

1 0

B

1

B

3

==

==

⎤

⎦

⎥⎥

(x) (x)dx = (

)(

)dx =

)dx = ( ) =

∫

1 0

B

1

B

1

∫

01 12

x

2 21

x

2

∫

0114

x

4 14 x 5 5

|

10 201

(x) (x)dx = (− + x + )(− + x + )dx = ( − 2 + x + )dx =

∫

1 0

B

2

B

2

∫

01

x

2 12

x

2 12

∫

01

x

4

x

3 14

( ) − 2(

x5

+ (

+ ( x) = + =

5

|

10 x44

)

10 x 2 2

)

10 14

|

10 15 14 209

(x) (x)dx = (

)(− + x + )dx = (− + + )dx =

∫

1 0

B

1

B

2

∫

01 12

x

2

x

2 12

∫

01 x 4 2 x 3 2 x 2 4

(− ) + ( ) + ( ) = − + +

x5

=

10

|

10 x84

|

10 12x3

|

10 101 18 121 12013

(x) (x)dx = (

)( (1 − x )dx = ( − + )dx =

∫

1 0

B

1

B

3

∫

01 12

x

2 12

)

2

∫

01 x 4 4 x 3 2 x 2 4

( ) − ( ) + ( ) =

x5

− +

=

20

|

10 x 4 8

|

10 x 3 12

|

10 201 18 121 1201

=

⎡

⎣

⎢⎢

⎢

(x) (x)dx

∫

1 0

B

1

B

1

(x) (x)dx

∫

1 0

B

2

B

1

(x) (x)dx

∫

1 0

B

3

B

1

(x) (x)dx

∫

1 0

B

1

B

2

(x) (x)dx

∫

1 0

B

2

B

2

(x) (x)dx

∫

1 0

B

3

B

2

(x) (x)dx

∫

1 0

B

1

B

3

(x) (x)dx

∫

1 0

B

2

B

3

(x) (x)dx

∫

1 0

B

3

B

3

⎤

⎦

⎥⎥

⎥

⎡

⎣

⎢⎢

1 20 13 120 1 120 13 120 9 20 13 120 1 120 13 120 1 20

⎤

⎦

⎥⎥

⎡

⎣

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢⎢

⎢

1 20 13 120 1 120

⋯

⋮

13 120

+

9 20 201

+

13 120 12013 1 120

⋮

⋯

1 120

+

13 120 12013

+ +

1 20 209 201

+

13 120 12013

⋮

1 120

⋯

⋯

1 120

+

13 120 12013

+ +

1 20 209 201

⋮

+

13 120 12013 1 120

⋯

⋯

1 120

+

13 120 12013

⋮

+ +

1 20 209 201

+

13 120 12013 1 120

⋯

⋯

1 120

⋮

+

13 120 12013

+ +

1 20 209 201

+

13 120 12013 1 120

⋯

⋮

1 120

+

13 120 12013

+

9 20 201 13 120 1 120 13 120 1 20

⎤

⎦

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥⎥

⎥

(x, y)

(x, y) =

(x)

(y)

Bk,l;2

B

x k;2

B

yl;2

v(x, y) =

Bk,l;2

(x, y)

(x, y)

Bk,l;2

(x) (y), (x) (y), (x) (y)

B

1

B

1

B

2

B

1

B

3

B

1

(x) (y), (x) (y), (x) (y)

B

1

B

2

B

2

B

2

B

3

B

2

(x) (y), (x) (y), (x) (y)

Rysunek 6: Podział dwuwymiarowego B-spline na poszczególne segmenty.

Tak więc problem liczenia całki bitmapy przemnożonej przez funkcję testującą B-spline sprowadza się do problemu policzenia dziewięciu całek. Na przykład, jeśli chcemy przeliczyć całkę dla B-spline'a testującego , wówczas musimy policzyć następujące dziewięć całek:

W powyższych wzorach wyrażenia typu oznaczają przeliczanie współrzędnych B-spline'a którego

całkujemy na indeksy pikseli bitmapy na których on się rozpościera.

Zmienne x i y zmieniają się od 0 do 1. W obrębie jednego elementu, mamy pikseli w kierunku

oraz pikseli w kierunku , gdzie oznacza rozmiar bitmapy (całkowitą liczbę pikseli w kierunku i )

natomiast oznacza liczbę elementów siatki w kierunku i . Tak więc zmienia się od 0 do ,

czyli obejmuje liczbę pikseli bitmapy w kierunku na pojedyńczym elemencie, natomiast zmienia się od 0 do liczby pikseli bitmapy w kierunku na pojedyńczym elemencie.

Dodatkowo przesuwamy nasz zakres tak żeby przeglądać piksele odpowiednich elementów na których rozpięty jest nasz B-spline

testujący. Na przykład wyrażenie oznacza że przesuwamy się po pikselach elementu numer w

kierunku , oznacza że przesuwamy się po pikselach elementu numer w kierunku ,

oznacza że przesuwamy się po pikselach elementu numer w kierunku . Podobnie

oznacza że przesuwamy się po pikselach elementu numer w kierunku , oznacza

że przesuwamy się po pikselach elementu numer w kierunku , oraz oznacza że przesuwamy się

po pikselach elementu numer w kierunku . Jak więc policzyć takie całki po pixelach?

Musimy rozbić całkę na sumę całek po poszczególnych pikselach, na przykład dla pierwszej całki

gdzie suma zaznaczona na czerwono rozpościera się po wszystkich pikselach z pojedynczego elementu (jest ich

), bitmapa jest próbkowana w punktach pikseli rozpostartych na danym elemencie, a całki zaznaczone na niebiesko, liczone są z funkcji B-spline po pojedynczych pikselach. Wystarczy teraz że policzymy pojedyncze całki z trzech segmentów

i wstawimy je do wzorów na całki, na przykład

Liczenie całek funkcji testujących z bitmapy zrobiło się trochę skomplikowane. Podsumujmy, musimy policzyć wiele całek z bitmapy, przemnożone przez różne dwuwymiarowe B-spliny, tak zwane funkcje testujące. Każdą z tych całek liczymy tak że rozbijamy ją na całkę po dziewięciu elementach na których rozpięty jest B-spline testujący, i sumujemy te wynikowe dziewięć całek, wpisując otrzymaną liczbę do jednego wiersza wektora prawej strony. Z kolei żeby policzyć całkę po każdym z tych dziewięciu elementów na których rozpięty jest nasz B-spline testujący, całki te rozbijamy na poszczególne piksele które leża na tym elemencie, próbkujemy naszą bitmapę po tych pikselach i liczymy całkę z naszych segmentów B-spline'ów po wszystkich pikselach. Wszystko to razem sumujemy (suma po dziewięciu elementach na których leży B-spline testujący, suma po pikselach elementów).

Rozwiązanie układu równań linowych

Rozwiązanie układu równań linowych

W wyniku generacji układu równań dostaliśmy macierz zapisaną w postaci produktu Kroneckera dwóch macierzy pięcio-przekątniowych, oraz prawą stronę policzoną z mozołem dla poszczególnych B-spline'ów testujących. Musimy teraz rozwiązać

(x, y)

Bk,l;2

(x) (y)BITMAP((k − 1 + x) ∗ maxx/ , (l − 1 + y) ∗ maxy/ )dxdy,

∫

1

0

∫

01

B

1

B

1

Nx

Ny

(x) (y)BITMAP((k + x) ∗ maxx/ , (l − 1 + y) ∗ maxy/ )dxdy,

∫

1

0

∫

01

B

2

B

1

Nx

Ny

(x) (y)BITMAP((k + 1 + x) ∗ maxx/ , (l − 1 + y) ∗ maxy/ )dxdy,

∫

1

0

∫

01

B

3

B

1

Nx

Ny

(x) (y)BITMAP((k − 1 + x) ∗ maxx/ , (l + y) ∗ maxy/ )dxdy,

∫

01

∫

01

B

1

B

2

Nx

Ny

(x) (y)BITMAP((k + x) ∗ maxx/ , (l + y) ∗ maxy/ )dxdy,

∫

1

0

∫

01

B

2

B

2

Nx

Ny

(x) (y)BITMAP((k + 1 + x) ∗ maxx/ , (l + y) ∗ maxy/ )dxdy,

∫

01

∫

01

B

3

B

2

Nx

Ny

(x) (y)BITMAP((k − 1 + x) ∗ maxx/ , (l + 1 + y) ∗ maxy/ )dxdy,

∫

1

0

∫

01

B

1

B

3

Nx

Ny

(x) (y)BITMAP((k + x) ∗ maxx/ , (l + 1 + y) ∗ maxy/ )dxdy,

∫

1

0

∫

01

B

2

B

3

Nx

Ny

(x) (y)BITMAP((k + 1 + x) ∗ maxx/ , (l + 1 + y) ∗ maxy/ )dxdy.

∫

1

0

∫

01

B

3

B

3

Nx

Ny

(k − 1 + x) ∗ maxx/N

x

maxx/Nx

x

maxy/Ny

y

maxx, maxy

x y

,

Nx

Ny

x y

x ∗ maxx/Nx

maxx/Nx

x

y ∗ maxy/Ny

y

(k − 1 + x) ∗ maxx/N

x

k

x (k + x) ∗ maxx/Nx

k + 1

x

(k + 1 + x) ∗ maxx/N

x

k + 2

x

(l − 1 + y) ∗ maxy/N

y

l

y (l + y) ∗ maxy/Ny

l + 1

y

(l + 1 + y) ∗ maxy/N

y

+2l

y

(x) (y)BITMAP((k − 1 + x) ∗ maxx/ , (l − 1 + y) ∗ maxy/ )dxdy =

∫

1

0

∫

01

B

1

B

1

Nx

Ny

BITMAP((k − 1) ∗ maxx/

+ i, (l − 1) ∗ maxy/

+ j)

∑

i=1,maxx/ ;j=1,maxy/Nx Ny

Nx

Ny

(x)dx

(y)dy

∫

_(i−1,i)∗ 1 maxx/Nx

B

1

∫

(j−1,j)∗maxy/Ny1

B

1

maxx/

Nx

∗ maxy/

Ny

∫ (x)dx = ∫

B

1 1₂

x

2

dx =

1₂x₃3

,

∫ (x)dx = ∫(− + x + )dx = − + + x,

B

2

x

2 12 x 3 3 x 2 2 12

∫ (x)dx = ∫ (1 − x dx = ∫(1 − 2x + ) = x − +

B

3 12

)

2

x

2

x

2 x 3 3

(x)dx

= (

)

= (

)

∫

(i−1,i)∗ 1 maxx/Nx

B

1 1 2x 3 3

|

i maxx/Nx i−1 maxx/Nx 1 2 − ( i−1 ) maxx/Nx 3 ( i ) maxx/Nx 3 3

(y)dy

= (

)

= (

)

∫

(j−1,j)∗ 1 maxy/Ny

B

1 1 2x 3 3

|

j maxy/Ny j−1 maxy/Ny 1 2 − ( j−1 ) maxy/Ny 3 ( j ) maxy/Ny 3 3