teo­ria do ćwi­cze­nia

Spis treści

POMIARY WIELKOŚCI FIZYCZNYCH I ICH BŁĘDY...1

METODY POMIAROWE...5

NIEPEWNOŚĆ POMIAROWA I METODY JEJ OKREŚLENIA...7

Niepewność standardowa pomiarów bezpośrednich...8

Ocena niepewności pomiarowej typu A...8

Ocena niepewności pomiarowej typu B...15

Niepewność standardowa pomiarów pośrednich ...17

Niepewność rozszerzona...21

Dokładność metody zerowej mostkowej - przykład...23

ROZKŁAD STATYSTYCZNY MAXWELLA...25

WSTĘP DO TEORII POMIARÓW

POMIARY WIELKOŚCI FIZYCZNYCH I ICH BŁĘDY

Pomiar jest podstawowym źródłem informacji w fizyce. Pomiarem nazywa się czynności doświadczalne mające na celu wyznaczenie wartości badanej wielkości fizycznej. Istotą każdego pomiaru jest porównanie wartości mierzonej z wzorcem miary tej wielkości przyjętym za jednostkę (np. pomiar długości w m, km itp.). Wynik pomiaru musi zatem składać się z dwóch części: wartości liczbowej, określającej ile razy

mierzona wielkość jest większa lub mniejsza od przyjętego wzorca oraz rodzaju jednostki.

Pomiary wielkości fizycznych dzielimy na bezpośrednie i pośrednie. Pomiary bezpośrednie polegają wprost na porównaniu danej wielkości z odpowiednią miarą wzorcową, wynik pomiaru otrzymuje się bezpośrednio bez wykonywania jakichkolwiek obliczeń.

W pomiarach pośrednich wartość badanej wielkości jest wyznaczana na podstawie pomiarów bezpośrednich innych wielkości fizycznych, które są z nią powiązane znanym prawem fizycznym, czyli występuje konieczność wyliczenia wartości wielkości mierzonej y na podstawie bezpośrednich pomiarów innych wielkości x1, x2,..., xn związanych z nią znaną zależnością funkcyjną y  f(x₁,x₂,x₃,....,x_n).

W trakcie pomiaru nigdy nie można bezwzględnie dokładnie wyznaczyć rzeczywistej wartości mierzonej wielkości, uzyskana wartość liczbowa zawsze różni się od przewidywań teorii. W odniesieniu do przyczyn tej rozbieżności używa się terminu błąd pomiaru. W tym zastosowaniu pojęcie błąd pomiaru występuje w znaczeniu jakościowym, natomiast w znaczeniu ilościowym błąd pomiarowy oznacza różnicę pomiędzy wynikiem pomiaru a rzeczywistą wartością. Błąd bezwzględny definiujemy jako różnicę wyniku pomiaru x i wartości rzeczywistej xR:

R

x x x 

 (1)

a błąd względny jako stosunek błędu bezwzględnego do wartości rzeczywistej: 1      R R x x x x x (2) Należy podkreślić, że pojęcie wartości rzeczywistej jest czysto teoretyczne, gdyż

praktycznie nie jest znana. Z tego względu operowanie wartością błędu jest utrudnione.

Uwzględniając przyczyny powstawania błędów występujących podczas wykonywania pomiarów można wyróżnić następujące trzy kategorie: błędy grube, błędy systematyczne i błędy przypadkowe.

Błędy grube powstają na skutek nieumiejętności użycia danego przyrządu, pomyłek przy odczytywaniu i zapisie wyników, nagłej zmiany warunków pomiaru itp. Dla błędów grubych różnica między wynikiem pomiaru i wartością rzeczywistą jest na ogół bardzo duża. Dla serii pomiarów wyniki obarczone błędem grubym są łatwe do wykrycia i usunięcia. Na wykresach mierzonych lub wyznaczanych wielkości punkty pomiarowe nie obarczone błędami grubymi układają się zgodnie z prawidłowością występująca w teorii badanego zjawiska, natomiast wyniki obarczone tym błędem odbiegają znacznie od pozostałych. Błędy grube eliminuje się poprzez:

 wychwytywanie ich w czasie wykonywania doświadczeń i powtarzanie odpowiednich pomiarów (uwaga słuszna, gdy eksperymentator posiada doświadczenie w przeprowadzaniu pomiarów),

 wychwytywanie ich w czasie opracowywania wyników, pojedyncze podejrzane przypadki należy eliminować, w przypadku pewnej liczby błędnych danych w serii należy poszukać przyczyn natury systematycznej. Pomiary są obarczone błędami systematycznymi, gdy przy powtarzaniu pomiarów dla serii pomiarowej występuje różnica między wartościami zmierzonymi a wartością rzeczywistą podlegająca pewnej prawidłowości, natomiast rozrzut wyników poszczególnych pomiarów jest niewielki lub w ogóle nie występuje. Błędy systematyczne wynikają z:

 mało dokładnego ustawienia eksperymentu (np. nieuwzględnienie siły wyporu powietrza przy dokładnym ważeniu),

 wad urządzeń pomiarowych (np. waga dźwigniowa z przesuniętym punktem zawieszenia, czasomierz wskazówkowy ze środkiem skali nie pokrywającym się z osią wskazówek, źle wyskalowane przyrządy),

 ze stanu zewnętrznych warunków pomiaru (zbyt wysoka temperatura w pomieszczeniu),

 niedoskonałości eksperymentatora (błąd paralaksy w trakcie odczytu wskaźników analogowych).

Obecnie błąd systematyczny można w pewnych wypadkach traktować jako zjawisko przypadkowe, gdyż nie znamy zazwyczaj jego wielkości i znaku. W tym ujęciu wykonując pomiar danym przyrządem dysponujemy tylko jedną realizacją zmiennej losowej. Losową próbkę można jednak uzyskać, jeżeli pomiary zostaną wykonane przy użyciu zbioru przyrządów o tej samej dokładności. Postępując w ten sposób można uzyskać doświadczalny rozkład prawdopodobieństwa dla błędu uważanego za systematyczny. Wynikające z tego konsekwencje matematyczne zostaną przedstawione przy omawianiu niepewności pomiaru.

Występowanie błędów przypadkowych objawia się jako rozrzut wyników pomiaru wokół wartości rzeczywistej. Wynik każdego kolejnego pomiaru jest inny. O tym jaka jest szansa uzyskania wyników większych lub mniejszych od x0 decyduje rodzaj rozkładu statystycznego (np. Gaussa, prostokątny, jednostajny), któremu te wyniki podlegają. Błędy przypadkowe wynikają z różnych przypadkowych i nie dających się uwzględnić

czynników. W fizyce klasycznej, gdzie większość zjawisk jest opisywana przez prawa deterministyczne, przyczyną statystycznego rozrzutu wyników pomiaru mogą być:

• niedokładność i przypadkowość działania ludzkich zmysłów (eksperymentator każdy kolejny pomiar wykona nieco inaczej),

• fluktuacji warunków pomiaru (wilgotność, temperatura, ciśnienie, zużycie elementów biorących udział w doświadczeniu),

• nieokreślenie samej mierzonej wielkości fizycznej,

• szumy (elektromagnetyczne, termiczne) generowane w samym układzie pomiarowym oraz zakłócenia zewnętrzne.

W ogólności przyczyny występowania błędów podczas pomiarów wynikają z: • niedoskonałości eksperymentatora,

• niedoskonałości przyrządów pomiarowych, • niedoskonałości metod pomiarowych, • niedoskonałości mierzonych obiektów, a analiza ich prowadzi do następujących wniosków:

• błędy grube należy całkowicie wyeliminować odpowiednio starannie przeprowadzając pomiary i uważnie analizując wyniki (wynik pomiaru nie powinien być obarczony ich wpływem),

• błędy systematyczne mogą być korygowane na etapie wyboru metody pomiarowej i analizy wyników pomiarów, ich granice powinny być wyraźnie określone,

• błędów przypadkowych ze względu na ich losowy (przypadkowy) charakter nie można całkowicie uniknąć ani skorygować, ale można minimalizować ich wpływ na wynik końcowy.

METODY POMIAROWE

Metoda pomiarowa to zastosowany podczas pomiaru sposób porównania wartości mierzonej z wzorcem miary tej wielkości. Istnieje wiele metod pomiarowych różniących się sposobem postępowania i zastosowanymi narzędziami. Uwzględniając sposób postępowania podczas pomiaru i rodzaj zastosowanych narzędzi pomiarowych, z czym wiąże się zwykle osiągalna dokładność wyniku, rozróżnia się metody bezpośredniego odczytu i metody porównawcze. Wśród metod porównawczych można wyróżnić następujące rodzaje: metodę różnicową, metodę przez podstawienie i metody zerowe.

W metodzie bezpośredniego odczytu, zwanej też metodą odchyleniową, wartość wielkości mierzonej zostaje określona na podstawie odchylenia wskazówki lub innego wskazania (np. cyfrowego) narzędzia pomiarowego. Podczas pomiaru wzorzec wielkości mierzonej nie występuje bezpośrednio, natomiast przy produkcji narzędzia pomiarowego cały szereg wartości wzorcowych został wykorzystany do odpowiedniego wykonania podziałki (wzorcowanie podziałki). Metoda ta jest najprostsza, najłatwiejsza w zastosowaniu, daje natychmiastowe wyniki, ale przy wykorzystaniu analogowych narzędzi pomiarowych jest stosunkowo mało dokładna. Dokładność metody znacznie zwiększyła się z chwilą zastosowania bardzo dokładnych przyrządów cyfrowych.

Niedokładność pomiaru wykonywanego tą metodą wynika głównie z istnienia dopuszczalnego błędu systematycznego narzędzia pomiarowego określonego jego klasą dokładności.

Metoda różnicowa jest metodą porównawczą, w której w układzie pomiarowym występuje wzorzec wielkości o wartości zbliżonej do wartości mierzonej (np. jednowartościowy wzorzec nienastawialny). W tym przypadku bezpośrednio mierzy się różnicę obu wartości, a wynik pomiaru określa się następująco: x x_W x, gdzie: xW – wartość wzorcowa, x – zmierzona bezpośrednio różnica z uwzględnieniem jej znaku.

Ponieważ wartość wzorcowa jest zwykle określona z pomijalnie małym błędem, błąd pomiaru wartości x wynika z niedokładności bezpośredniego pomiaru różnicy x.

Metoda pomiarowa przez podstawienie jest metodą porównania bezpośredniego. W układzie pomiarowym znajduje się wzorzec wielkości mierzonej o wartościach nastawianych w szerokich granicach. Podczas pomiaru wartość mierzoną x zastępuje się wartością wzorcową xW dobraną w taki sposób, aby skutki (np. odchylenia wskazówki miernika) wywoływane przez obie wartości były takie same, z czego wynika zależność:

W

x x  .

Metoda przez podstawienie jest metodą bardzo dokładną, ponieważ praktycznie eliminuje błędy wprowadzane przez układ porównania. Po wielokrotnym powtórzeniu pomiaru i obliczeniu wartości średniej (zminimalizowaniu błędów przypadkowych) błąd wyniku pomiaru jest praktycznie równy błędowi dopuszczalnemu dla wzorca.

Metody pomiarowe zerowe są najdokładniejszymi metodami porównania bezpośredniego. Porównanie wartości mierzonej z wartością wzorcową (lub z zespołem wartości wzorcowych) odbywa się za pomocą układu pomiarowego, w którym przez zmianę parametrów elementów składowych doprowadza się do zaniku (do zera) napięcia lub prądu w kontrolowanej gałęzi układu. Czynność doprowadzania do zaniku napięcia lub prądu nazywa się równoważeniem układu, a wskaźnik służący do zaobserwowania tego stanu (np. galwanometr) nazywa się wskaźnikiem równowagi. Dokładność zerowych metod pomiaru jest bardzo duża, zależy od dokładności wykonania zastosowanych w układzie wzorców oraz od czułości wskaźnika równowagi. Zastosowanie bardzo dokładnych wzorców oraz zastosowanie wskaźnika równowagi o wysokiej czułości ogranicza błędy systematyczne metody do wartości pomijalnych wobec błędów przypadkowych. Podczas dokładnych pomiarów wykonuje się zwykle serię pomiarów i statystyczną analizę wyników pomiaru.

Rozróżniamy zerowe metody mostkowe oraz zerowe metody kompensacyjne. Metody mostkowe stosuje się najczęściej do dokładnych pomiarów takich parametrów jak rezystancja, pojemność i indukcyjność w układach z prądem stały lub przemienny.

Metody kompensacyjne służą zwykle do pomiaru napięcia lub do pośredniego pomiaru innych wielkości przetworzonych uprzednio na napięcie. W metodzie kompensacyjnej nieznaną wartość napięcia mierzonego U porównuje się z nastawianą dokładnie znaną wartością wzorcową UW, wytworzoną za pomocą kompensatora. Układ pomiarowy doprowadza się do równowagi przez zmianę wartości UW, a w chwili równowagi zachodzi równość: U UW. Szczególnie ważną zaletą metod kompensacyjnych jest to,

że w chwili zrównoważenia układu przez badany obiekt nie płynie prąd, zatem nie występuje błąd systematyczny metody, wynikający ze spadku napięcia na rezystancji wewnętrznej obiektu badanego.

NIEPEWNOŚĆ POMIAROWA I METODY JEJ OKREŚLENIA

Z istoty natury pomiaru wynika zatem, że nie można nigdy niezależnie od metody pomiarowej, bezwzględnie dokładnie wyznaczyć rzeczywistej wartości wielkości fizycznej, czyli dokonać pomiaru absolutnie dokładnego. Pomiary mogą być wykonywane tylko ze skończoną dokładnością. Ponieważ nie jest znana nigdy rzeczywista wartość mierzonej wielkości posługiwanie się pojęciem błędu pomiaru, zdefiniowanym jako różnica pomiędzy wynikiem pomiaru a wartością rzeczywistą, jest niewygodne. Podawanie tylko wyniku pomiaru jest jednak niewystarczające, opracowanie wyników pomiaru powinno zawierać także ocenę ich wiarygodności, czyli niepewność pomiaru. Takie podejście jest zgodne z zaleceniami Międzynarodowej Normy Oceny Niepewności Pomiaru [1], uzgodnionej w 1995 r. i przyjętej ustawowo w Polsce w 1999 roku [2].

Niepewność pomiaru jest ogólnie zdefiniowana jako parametr związany z rezultatem pomiaru, charakteryzujący rozrzut wyników, który można w uzasadniony sposób

przypisać mierzonej wartości. Pojęciem jakościowym związanym z terminem niepewność jest dokładność. Pomiarem dokładniejszym jest pomiar o mniejszej niepewności.

Miarą niepewności pomiarowej jest niepewność standardowa, która może być szacowana na dwa sposoby:

 ocena typu A – wynika ze statystycznej analizy serii n równoważnych i nieskorelowanych obserwacji wielkości x podlegającej błędowi przypadkowemu,

 ocena typu B – wynika z naukowego osądu eksperymentatora, biorącego pod uwagę wszystkie posiadane informacje o pomiarze i źródłach jego niepewności. Stosowana jest w przypadku niemożności przeprowadzenia statystycznej analizy serii pomiarów np. dla błędu systematycznego.

Jako symbol niepewności standardowej przyjęto oznaczenie u (od angielskiego słowa

uncertainity), które może być zapisane na trzy sposoby:

 u – niepewność standardowa dowolnej wielkości

 u(x) – niepewność standardowa wielkości x wyrażonej symbolem

 u(długość wahadła) – niepewność wielkości wyrażonej słownie.

Niepewność względna jest definiowana jako stosunek niepewności standardowej do wielkości mierzonej:

 

 

x x u x u_r  (W.3)

Wymiar niepewności standardowej u(x) jest taki sam jak wymiar wielkości mierzonej, natomiast niepewność względna jest wielkością bezwymiarową, co umożliwia porównywanie za jej pomocą niepewności wielkości fizycznych posiadających różny wymiar.

Niepewność standardowa pomiarów bezpośrednich

Ocena niepewności pomiarowej typu A

Ocena niepewności pomiarowej typu A dotyczy określenia niepewności dla pomiarów obarczonych błędami przypadkowymi. Z jednego pomiaru nie można wnioskować o jego

dokładności. Dlatego konieczne jest wykonanie serii n bezpośrednich pomiarów wielkości fizycznej x, poprzez wielokrotne, niezależne powtórzenie rozpatrywanego pomiaru. Wyniki w serii będą różnić się losowo, oznaczmy je x1, x2, x3, ... xn, gdzie n jest ilością powtórzeń pomiaru w serii. Wyniki można traktować jako n realizacji zmiennej losowej o wartości oczekiwanej xo (utożsamianej z wartością rzeczywistą) oraz odchyleniu standardowym  i stosować standardowe rezultaty teorii błędów. Wartość

rzeczywista jest nieznana, ale w większości przypadków dla serii pomiarów najlepszym oszacowaniem mierzonej wartości jest średnia arytmetyczna:



  n i i x n x 1 1 (W.4)

Jest to podstawowe twierdzenie teorii pomiarów tzw. pierwszy postulat Gaussa. Wynika ono z faktu równości prawdopodobieństw zawyżenia jak i zaniżenia wielkości mierzonej. Tym samym błędy powinny kompensować się. Przy skończonej ilości pomiarów w serii może jednak wystąpić nierównomiernie rozłożenie wyników wokół wartości rzeczywistej. Tym samym wartość średnia x jest jedynie bliska wielkości rzeczywistej

xR, ale jej nie równa. Zbliżenie to jest tym lepsze im dłuższa jest seria pomiarowa. Równość x  x_R występuje tylko dla nieskończenie dużych serii pomiarów, praktycznie niemożliwej do wykonania.

W serii wyniki pomiarów rozkładają się wokół wartości średniej w tzw. krzywą Gaussa. Aby się o tym przekonać należy zakres pomiarowy podzielić na przedziały o równej szerokości x i obliczyć, ile pomiarów z serii mieści się w każdym z nich (rys. 1).

Oczywiście zwiększając n można zmniejszyć szerokości poszczególnych przedziałów rozkładu, ale nadal zostanie zachowany jego dyskretny charakter. Obwiednia dzwonowa poprowadzona po środkach przedziałów (patrz rys. 1) jest pewnym wyidealizowaniem, pokazuje wygląd rozkładu normalnego, gdyby był funkcją ciągłą (dla n). Taka postać łatwiej poddaje się analizie matematycznej i dlatego jest często stosowana, ale nie należy zapominać, że realny rozkład normalny ma strukturę ziarnistą. Ciągły rozkład Gaussa jest następującą funkcją matematyczną:

 

  2 2 2 2 1  _    x x e x P (W.5)

gdzie parametr  , zwany w statystyce odchyleniem standardowym, określa rozkład wyników pomiarów wokół wartości średniej.

Kształt krzywej Gaussa, zwanej również krzywą dzwonową, bardzo silnie zależy od wartości odchylenia standardowego  . Na rys. 2 pokazano przebiegi krzywej Gaussa dla kilku różnych wartości odchylenia standardowego. Dla małych odchyleń standardowych krzywa jest bardzo stroma i odchylenia od wartości oczekiwanej są bardzo małe. Im większe odchylenie standardowe tym krzywa jest bardziej płaska. Zauważmy, że na krzywej Gaussa można wyróżnić obszary o przeciwnie skierowanej krzywiźnie. W okolicy maksimum krzywa jest wypukła, a daleko poza maksimum wklęsła. Obszary o przeciwnej krzywiźnie są oddzielone punktami przegięcia, odpowiadają im na osi odciętych punkty x i x.

Ponieważ rozkład Gaussa opisuje zjawisko probabilistyczne można określić jedynie prawdopodobieństwo znalezienia się dowolnego wyniku pomiaru xi (i = 1, 2, 3....n) w określonym przedziale wartości x ,A xB . I tak:

 w przedziale x,x mieści się 68,26% wyników z serii,  w przedziale x2,x2 mieści się 95,45% wyników z serii,  w przedziale x3,x3 mieści się 99,73% wyników z serii.

Prawdopodobieństwo, że dany wynik pomiaru z serii pomiarowej znajdzie się w przedziale x,x wynosi zatem 0,683. Prawdopodobieństwo, z jakim w zadanym przedziale znajdzie się dowolny pomiar z serii nosi nazwę poziomu ufności, a przedział przedziału ufności.

Rys. 1. Rozkład pomiarów w serii wokół wartości średniej x jest rozkładem Gaussa.

Rys. 2. Przebieg krzywej ciągłego rozkładu normalnego w zależności od odchylenia standardowego. Im większe jest odchylenie standardowe, tym krzywa jest szersza i

Rys. 3. Interpretacja graficzna przedziałów ufności i poziomów ufności p oraz współzależność między nimi.

W interpretacji graficznej prawdopodobieństwu znalezienia wyniku pomiaru w odpowiednim przedziale odpowiada pole pod krzywą Gaussa odcięte tym przedziałem przy założeniu, że pole pod całą krzywą równa się jeden (rys. 3a, 3b).

Analiza kształtu krzywej Gaussa prowadzi do wniosku, że wybór przedziału 

 

 x

x , jako określającego rozrzut wyników pomiarów wokół wartości średniej jest najbardziej optymalny, co wynika z faktu, że jest on wyznaczony przez punkty przegięcia krzywej. Sztuczne zmniejszenie przedziału ufności do x ,d xd (rys. 3c) prowadzi do znacznego obniżenia poziomu ufności (o pole pod krzywą Gaussa odcięte przedziałami x , xd , x , xd , które jest duże, bo na tych odcinkach krzywa Gaussa jest wypukła). Podniesienie poziomu ufności (rys. 3d) jest możliwe tylko przez znaczne poszerzenie przedziału ufności do x ,c xc , gdyż pola pod krzywą w przedziałach oddalonych od średniej x dalej niż o  wnoszą mały wkład do poziomu ufności (krzywa Gaussa na tych obszarach jest wklęsła).

Odchylenie standardowe  w teorii pomiarów przyjmuje się za miarę rozrzutu wyników pomiaru i definiuje sią jako niepewność standardową pojedynczego pomiaru, którą oblicza się przy pomocy wyrażenia:

 







1



1 2    



 n x x x u n i i  (W.6)

Występujący w wyrażeniu czynnik



n1



można uzasadnić faktem, że ponieważ część informacji zawartej w serii x1,x2,x3, ... xn została wykorzystana do określenia wartości średniej x , uśrednianie związane z odchyleniem standardowym następuje z mniejszą liczbą punktów swobody i stąd dzielenie przez



n1



zamiast przez n.

Natomiast dla wartości średniej x uznawanej za wynik serii n pomiarów jako niepewność standardową przyjmuje się odchylenie standardowe wartości średniej  ix

wynosi ona:

 









 

n x u n n x x x u n i i x     



 1 1 2  (W.7)

Wartość niepewności standardowej wartości średniej jest n razy mniejsza od niepewności standardowej pojedynczego pomiaru. Wartości niepewności standardowych

 

x

u lub u

 

x , choć wyznaczone przy pomocy jednoznacznych wzorów są równe prawdziwym wartościom odchylenia standardowego i odchylenia standardowego średniej tylko w granicy dla nieskończonej ilości pomiarów. Dla skończonej liczby pomiarów niepewność pomiaru jest określona ze skończoną dokładnością. Przyjmuje się, że dla wyznaczenia niepewności standardowej jako odchylenia standardowego należy wykonać 510 pomiarów, co pozwala na ocenę niepewności pojedynczego pomiaru rzędu 2030%. Wykonywanie zbyt dużej liczby pomiarów nie jest opłacalne, ponieważ dokładność wyznaczenia niepewności dość powoli zwiększa się ze wzrostem n ilości pomiarów.

Reasumując wykonanie serii n pomiarów umożliwia:

 oszacowanie niepewności spowodowanych błędami przypadkowymi,  zwiększenie dokładność niepewności.

Wykonanie niewielkiej liczby 2 lub 3 pomiarów można przyjąć jako sprawdzian powtarzalności, za wynik pomiaru należy wówczas przyjąć średnią, a dla oceny niepewności pomiaru stosować ocenę typu B.

Trzeba zdecydowanie silnie podkreślić, że same parametry rozkładu ( x ,σ)nie dają pełnej informacji statystycznej. Taką informacją jest jedynie wykres rozkładu w postaci dyskretnej (tzw. histogram) lub w postaci ciągłej. Punkty eksperymentalnie otrzymanego histogramu niejednokrotnie znacznie odbiegają od teoretycznej krzywej Gaussa,

ponieważ N nie jest wystarczająco duże. W ćwiczeniu w celu ułatwienia otrzymania docelowej ciągłej krzywej rozkładu stosujemy metodę Simpsona umożliwiającą przeliczenie punktów eksperymentalnych P(xi ) na punkty położone bliżej docelowej

krzywej PS(xi ) i w związku z tym ułatwiające jej znalezienie. Zależność Simpsona ma postać:



( ) ( ) ( )



, ) ( _i  025 _i1 2 _i  _i1 S x P x P x P x P (1.1)

i jest właściwością krzywej Gaussa określającą współzależność trzech sąsiednich punktów pomiarowych. Parametry rozkładu normalnego można wyznaczyć następującymi sposobami:

średnia x : na bazie wzoru (W.4); z wykresu rozkładu normalnego - jako miejsce położenia jego maksimum;

odchylenie standardowe σ : na bazie wzoru (W.6); z wykresu rozkładu normalnego określając położenie punktów przegięć.

Ocena niepewności pomiarowej typu B

Ocena niepewności pomiarowej typu B jest stosowana, gdy statystyczna analiza serii pomiarów nie jest możliwa. Taka sytuacja zachodzi dla błędu systematycznego lub dla błędu przypadkowego, gdy dostępnych jest tylko kilka rezultatów pomiaru. Co ma miejsce, gdy ze względów eksperymentalnych nie ma możliwości powtórzenia doświadczenia.

Ocena niepewności typu B opiera się na naukowym osądzie eksperymentatora, możliwie obiektywnym, wykorzystującym wszystkie informacje o pomiarze i źródłach jego niepewności. W tym celu może on wykorzystać między innymi:

 doświadczenie i wiedzę na temat przyrządów i obiektów mierzonych,

 informacje producenta przyrządów (np. klasę przyrządów, działkę elementarną),

 dane z poprzednich pomiarów,

 niepewności przypisane danym zaczerpniętym z literatury.

Ocena niepewności typu B polega na oszacowaniu niepewności maksymalnej, oznaczanej symbolem  (duża delta), czyli największej jaka może wystąpić w danym pomiarze.

Najczęściej ocena typu B dotyczy określenia niepewności wynikających ze skończonej dokładności przyrządów. Aktualnie prawie wszystkie używane przyrządy pomiarowe to proste przyrządy mechaniczne lub elektroniczne mierniki cyfrowe. Dla prostych przyrządów mechanicznych, do których można zaliczyć linijkę, termometr, śrubę mikrometryczną, jako niepewność maksymalną przyjmuje się działkę elementarną

przyrządu, np. oszacowana niepewność maksymalna pomiaru temperatury przy pomocy typowego termometru wynosi Δt1o C.

W elektronicznych przyrządach cyfrowych wartość odpowiadająca zmianie ostatniej cyfry, zwana działką elementarną, określa rozdzielczość przyrządu. Niepewność maksymalna zazwyczaj jest kilkakrotnie większa od działki elementarnej. Podawana jest przez producenta przyrządu i najczęściej zależy od wielkości mierzonej x oraz zakresu z, na którym dokonuje się pomiaru i wyznaczana jest z zależności: xc₁xc₂z.

Jeśli za pomocą woltomierza, dla którego podane przez producenta wartości c1 i c2

wynoszą odpowiednio: c1=0,2% i c2=0,1% zmierzono napięcie o wartości U = 98,25 V na

zakresie z = 150 V, to niepewność maksymalna tego pomiaru jest równa 0,35 V.

Na końcowy wynik oszacowania niepewności oprócz dokładności przyrządów składa się również dokładność samego eksperymentatora. Własną niepewność odczytu, czy niedoskonałość zmysłów, szczególnie trudno jest ocenić. Podczas pomiaru czasu przy pomocy stopera należy uwzględnić szybkość reakcji fizjologicznej podczas jego włączania i wyłączania, która może być rzędu 0,2 s lub mniejsza. Można ją oszacować próbując kilkukrotnie zatrzymać stoper na określonej pozycji. Łączna niepewność pomiaru czasu jest dwukrotnie większa, ponieważ niedokładności włączania i wyłączania stopera sumują się. W wyniku takiej analizy może się okazać, że w celu zwiększenia dokładności pomiaru użycie precyzyjniejszego stopera jest bezcelowe. Lepszym rozwiązaniem będzie zastosowanie elektronicznego pomiaru czasu z użyciem fotokomórki.

Jak wynika z określenia niepewności maksymalnej, jeśli nie występują żadne dodatkowe informacje, wynik pomiaru powinien wystąpić z jednakowym prawdopodobieństwem w przedziale x. Dla rozkładu jednostajnego, który występuje w tym przypadku jako

odchylenie standardowe przyjmuje się połowę szerokości rozkładu podzieloną przez 3 . Zgodnie z zaleceniami normy [1] zaleca się niepewność standardową wyrazić poprzez niepewność maksymalną za pomocą wzoru:

 

3

x x

Gdy występują oba typy niepewności zarówno statystyczny rozrzut wynikający z błędów przypadkowych jak i niepewność wynikająca z dokładności przyrządów i obie są tego samego rzędu, to żadna z nich nie może być pominięta. W tym przypadku całkowita niepewność standardową wyraża się wzorem:

 

 

3 2 2 x x u  _x   (W.9)

Niepewność standardowa pomiarów pośrednich

Wiele wielkości fizycznych nie można wyznaczyć jako wynik pomiaru bezpośredniego. Takie wielkości są związane z k innymi wielkościami fizycznymi x1, x2,...xk wyznaczanymi z pomiarów bezpośrednich odpowiednią zależnością funkcyjną:



x x xk



f

y ₁, ₂,..., (W.10)

Po przeprowadzeniu pomiarów znane są wyniki x , ₁ x ,...., ₂ x_k i niepewności standardowe u

 

x₁ , u

 

x₂ , ...., u

 

xk mierzonych wielkości x1 , x2 ,...xk.

Jako wynik pomiaru wielkości y przyjmuje się wielkość y wyznaczoną z zależności:



x x xk



f y

y  1, 2,..., (W.11)

Wartość y obarczona jest pewną skończoną niepewnością u_c

 

y , na która przenoszą się niepewności standardowe wielkości mierzonych bezpośrednio u

 

x1 , u

 

x2 ,.., u

 

xk .

Niepewność u_c

 

y nosi nazwę niepewności złożonej (od angielskiego terminu

combined uncertainty), a sposoby jej obliczania to prawo przenoszenia niepewności lub

prawo propagacji niepewności.

W przypadku pomiarów bezpośrednich nieskorelowanych tzn. gdy każdą z wielkości x1 , x2 ,...xk wyznacza się niezależnie, bezwzględną niepewność złożoną uc

 

y wielkości y

szacuje się przy pomocy następującego wzoru:

 

 

 

 

_

 

                                              k i i i k k c u x x y x u x y x u x y x u x y y u 1 2 2 2 2 2 2 1 1 ... (W.12)

Pochodne cząstkowe i x y  

oblicza się różniczkując związek y f



x1,x2,...,xk



względem zmiennej x traktując pozostałe zmienne jak stałe.i

Prawo przenoszenia niepewności przyjmuje przejrzystą i wygodną do praktycznych obliczeń postać, gdy zamiast niepewności złożonej bezwzględnej zostanie wyznaczona niepewność złożona względna u_c,r

 

y :

 

 

y y u y u_c,r  c (W.13)

W tym celu wyrażenie (W.12) dzielimy obustronnie przez y, a następnie wyrażenia wewnątrz nawiasów po prawej stronie równości mnożymy i dzielimy przez x , cok

prowadzi do postaci:

 

 



            k i i i i i c x x u y x x y y y u 1 2 (W.14)

Niepewność złożoną względną można zatem wyrazić jako sumę geometryczną

niepewności względnych

 

i i x x u

wielkości mierzonych bezpośrednio pomnożonych przez

bezwymiarowe wagi w w postaci i

y x x y w i i i    , czyli

 

 





 



 k i i r i r c y w u x u 1 2 , (W.15)

Jeśli zależność funkcyjna pomiędzy wielkościami x1, x2,...xk wyrażona jest w postaci potęgowo – iloczynowej typu:

k n k n n x x x C y  1  2 ... 2 1 (W.16) to wagi y x x y w i i i    są odpowiednio równe:





i n k n i n n i i n k n i n n i i i n x x x x C x x x x x x C y x x y w k i k i                    ... ... ... ... 2 1 2 1 2 1 2 1 (W.17)

czyli niepewność złożona względna wielkości y wyraża się zależnością:

(W.18)

W szczególnym przypadku jeśli wielkość y wyraża się zależnością iloczynowo - ilorazową wielkości x1, x2,...xk, przy obliczaniu wag otrzymuje się jako wynik jedność. W tym przypadku złożona niepewność względna jest sumą geometryczną względnych niepewności wielkości x :i

 

_



 



  k i i r c r c y u x u 1 2 , , (W.19)

Wartości wag dla najczęściej spotykanych funkcji zebrane są w poniższej tabeli, gdzie symbol C oznacza nie tylko stałą, ale również pozostałą cześć wzoru funkcyjnego nie zawierającą zmiennej x , czyli stanowiącą czynnik stały przy obliczaniu odpowiedniej_i

pochodnej cząstkowej.

typ zależności funkcyjnej waga

y x x y w i i i    n Cx y  n ax Ce y  ax

 

ax C y  ln 1/ln

 

ax

Otrzymane zgodnie z prawem przenoszenia niepewności wyrażenie (W.12) wiążące niepewność złożoną u_c

 

y wielkości y z niepewnościami standardowymi u

 

x1 , u

 

x2 ,..,

 

xk

u wielkości x1, x2,...xk mierzonych bezpośrednio jest słuszne zarówno w przypadku

 

 

_



 



_

 

               k i i i i k i i r i c r c x x u n x u n y y u y u 1 2 1 2 ,

wyznaczenia niepewności u

 

x₁ , u

 

x₂ ,.., u

 

xk z zastosowaniem metody oceny

niepewności typu A jak i oceny typu B.

Jeżeli bezpośrednie pomiary wielkości x1, x2,...xk pozwalają jedynie na zastosowanie metody oceny niepewności typu B, czyli wyznaczenie niepewności maksymalnych  ,x₁

2

x

 ,...x_k, wówczas uwzględniając jednostajny rozkład mierzonych wielkości w przedziałach xi x_i należy zgodnie z wyrażeniem (W.8) obliczyć niepewności standardowe pomiarów bezpośrednich jako:

 

3 i i x x u  _(W.20)

W tym przypadku wyrażenie opisujące niepewność złożoną sprowadza się do postaci:

 

_

                                                  k i i i k k c x x y x x y x x y x x y y u 1 2 2 2 2 2 2 1 1 3 1 ... 3 1 (W.21)

a dla zależności potęgowo – iloczynowej (W.16) niepewność złożona względna

 

 

_

             k i i i i c r c x x n y y u y u 1 2 , 3 1 (W.22)

Prawidłowo przeprowadzony rachunek błędów, automatycznie odpowiada na pytania:  które wielkości fizyczne x należy zmierzyć z większą dokładnością dlai

uzyskania zmniejszenia niepewność pomiarowej wielkości wynikowej y;  która niepewność standardowa bezwzględna u

 

xi wnosi największy wkład

do policzonej niepewności złożonej uc,r

 

y

Otrzymane wnioski z analizy błędów są ważne i pouczające, pozwalają na ewentualne efektywniejsze powtórzenie doświadczenia.

Niepewność rozszerzona

Niepewności standardowa u

 

x i niepewność złożona u_c

 

y wyznaczają przedziały domknięte, takie że prawdopodobieństwo znalezienia wartości rzeczywistej pomiaru odpowiednio w przedziale od x u

 

x do x u

 

x lub od yu_c

 

y do yu_c

 

y wynosi 0,683. Niepewności te są miarą dokładności pomiarów i umożliwiają porównywanie dokładności różnych metod pomiarowych.

Aby wyciągać wnioski o zgodności wyniku pomiaru z innymi wynikami Międzynarodowa Norma Niepewności Pomiarów [1] wprowadza pojęcie niepewności rozszerzonej (z języka angielskiego expanded uncertainty), oznaczanej U

 

x . Niepewność rozszerzoną wybiera się tak, aby w przedziale U

 

x , zwanym przedziałem objęcia znajdowała się przeważająca większość wyników pomiaru, potrzebna do określonych zastosowań. Wartość niepewności rozszerzonej U

 

x jest iloczynem niepewności standardowej i bezwymiarowego współczynnika rozszerzenia k:

 

x k u

 

x

U   (W.23)

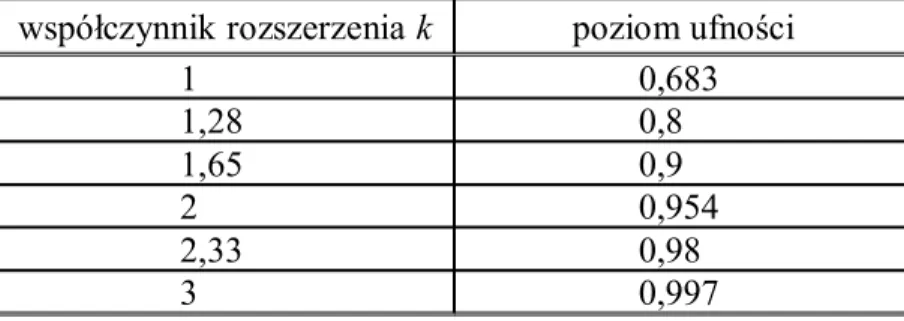
Tak zdefiniowany przedział objęcia można utożsamiać z przedziałem ufności, a prawdopodobieństwo objęcia z poziomem ufności. Przykładowe poziomy ufności dla kilku najczęściej stosowanych współczynników k podaje poniższa tabela:

Tabela 1. Poziomy ufności dla wybranych współczynników rozszerzenia k. współczynnik rozszerzenia k poziom ufności

1 0,683 1,28 0,8 1,65 0,9 2 0,954 2,33 0,98 3 0,997

W przypadku oceny typu B dla niepewności standardowej przedział objęcia nie ma ścisłej interpretacji statystycznej. W zgodzie z międzynarodową praktyką do obliczenia niepewności rozszerzonej przyjmuje się wówczas domyślnie wartość k=2, wartości inne

niż 2 mogą być stosowane tylko w wyniku decyzji uprawnionego eksperta i powinny wynikać z ustalonych i udokumentowanych wymagań [3].

Typowe zastosowania niepewności rozszerzonej to wnioskowanie o zgodności uzyskanego wyniku z wartością dokładną: teoretyczną (określoną przy pomocy teorii) lub tabelaryczną np. stałą przyrody, wyznaczoną w wyniku pomiarów, ale aktualnie znaną z bardzo dużą dokładnością. Porównanie wartości zmierzonej x z wartością dokładną x0 polega na porównaniu różnicy x x0 z niepewnością rozszerzoną U

 

x . Jeśli spełniony

jest warunek:

 

x U x

x ₀  (W.24)

to wartość zmierzoną uznajemy za zgodną z wartością dokładną.

Aby określić, czy wyniki dwóch niezależnych pomiarów tej samej wielkości x1 i x2 są równe w granicach niepewności pomiaru, należy porównać różnicę tych wyników z niepewnością rozszerzoną tej różnicy. Jeśli niepewności standardowe pomiarów są równe odpowiednio u

 

x₁ i u

 

x₂ , to zgodnie z prawem przenoszenia błędów niepewność standardowa różnicy jest równa sumie geometrycznej u

 

x₁ , u

 

x₂ :







 





 



2 2 2 1 2 1 x u x u x x u    (W.25) a niepewność rozszerzona:







 





 



2 2 2 1 2 1 x k u x u x x U     (W.26)

Dokładność metody zerowej mostkowej - przykład

Z zasada budowy i równoważenia mostka Wheatstone’a jest zgodna z rysunkiem przedstawionym poniżej, gdzie l l2l3 to całkowita długość drutu.

Ramię AC – odpowiada mierzonej rezystancji RX, zaś ramię AD – wzorcowej rezystancji zatyczkowej R4. Wielkości rezystancji R2 i R3 (odcinki drutu ślizgowego) zależą od położenia suwaka reochordu. Przy przesuwaniu jego suwaka zmieniają się wielkości rezystancji R2 i R3, a w związku z tym ich stosunek. Pomiar nieznanej

rezystancji sprowadza się do znalezienia takiego położenia suwaka reochordu, przy którym przez galwanometr nie płynie prąd. Powyższa operacja nosi nazwę równoważenia mostka. W rzeczywistych układach dodatkowo instaluje się komutator służący do zamiany miejscami rezystancji włączonych w ramiona mostka bez przełączania przewodów. Stosowanie komutatora jest wskazane z tego powodu, że drut reochordu nie bywa całkowicie jednorodny wzdłuż całej długości i dlatego stosunek R2 / R3 nie jest

dokładnie równy stosunkowi l2/l3. Obwód zasilany jest prądem stałym.

Zastosujemy teraz rachunek niepewności do wyznaczenia najlepszego punktu pomiaru. Mimo braku znajomości wartości mierzonych i ich niepewności będzie można wyznaczyć jak przeprowadzić ćwiczenie, by rezultaty były obarczone jak najmniejszą niepewnością. Wartość tej niepewności będzie można wyznaczyć po wykonaniu ćwiczenia.

W przypadku, gdy oporniki R2, R3 są odcinkami drutu ślizgowym, warunek równowagi mostka ma postać:

2 2 4 3 2 4 l l l R l l R R_X    _(P.1) gdyż: S l R 2 2  i S l R 3 3   . (P.2)

gdzie: l l2l3 – całkowita długość drutu,  – opór właściwy drutu, S – powierzchnia

przekroju drutu.

Rozpatrzmy zależność (P.1), z której metodą pośrednią określamy wartość nieznanej rezystancji RX. Mierzymy l2 z niepewnością maksymalną  . Wartość l oraz Rl2 4 zostały

zmierzone ze znacznie większą precyzją. Załóżmy, że ich niepewności maksymalne wynoszą odpowiednio l oraz R4. Wówczas niepewność złożona bezwzględna

wyznaczanej rezystancji wyniesie (patrz wzór W.21):





2 4 4 2 2 2 2 3 1 R R R l l R l l R R u_{c X} X X X             (P.3)

Przy pominięciu wkładów od błędu l oraz R4 jako znacznie mniejsze od wkładu

pochodzącego od  powyższy wzór przyjmuje postać:l2





₂ 2 2 4 ) ( 3 1 l l l l R R u_{c X}     _(P.4) a niepewność względna:









) ( 3 1 2 2 2 , l l l l l R R u R u X X c X r c      _(P.5)

Niepewność względna osiąga minimum dla takiej wartości l2, przy której mianownik powyższego wyrażenia osiąga maksimum. Łatwo zauważyć, że warunek ten ma miejsce dla l ₂ l 2, czyli w sytuacji, gdy l 2 l3 (tzn. R2 = R3). Wówczas spełniony jest warunek

RX = R4. Dla tej szczególnej sytuacji niepewność względną wyznaczanej rezystancji możemy wyrazić niepewnością względną zmierzenia długości l2:





2 2 , 3 2 l l R u_{cr X}   _(P.6)

Wzór powyższy możemy stosować, gdy RX mało różni się od R4, czyli gdy l2 jest bliskie 2

l

.

Poszukiwaną wartość niepewności będzie można wyznaczyć po wykonaniu ćwiczenia ze wzoru (P.6) gdy suwak reochordu znajduje się blisko połowy długości drutu ślizgowego.

ROZKŁAD STATYSTYCZNY MAXWELLA

W mechanice klasycznej pełnej informacji o cząsteczce dostarczają funkcje położenia oraz prędkości. Zazwyczaj można je zapisać w postaci f



r,v



R

   

rV v . Analogicznej informacji w ramach termodynamiki (opisu statystycznego) dostarczają funkcje rozkładu prawdopodobieństwa znalezienia w gazie cząsteczki, która:

• ma prędkość z przedziału



V, VdV



,

• znajduje się w pewnym obszarze (np. na wysokości z przedziału



h, hdh



). Stan gazu możemy też opisać podając jego temperaturę, ciśnienie, zajmowaną objętość, masę lub ilość moli. Pierwsze dwa parametry związane są z prędkościami z jakimi poruszają się cząsteczki gazu. Z drugiej strony znajomość tych parametrów nie pozwala jeszcze określić z jakimi konkretnymi prędkościami poruszają się poszczególne

cząsteczki gazu.

Cząsteczki gazu poruszają się chaotycznie, co oznacza, że wszystkie kierunki ruchu są jednakowo prawdopodobne. Wartości prędkości cząsteczek są różne i obejmują szeroki przedział wartości. Gdyby wszystkie cząstki miały taką samą prędkość, to sytuacja taka nie mogłaby trwać długo ponieważ w gazie dochodzi do zderzeń.

Zakładając nawet, że są to tylko zderzenia sprężyste jednakowych cząsteczek, nie są to tylko zderzenia centralne. Zderzenia niecentralne zmieniają wektory prędkości

cząsteczek (wartości i kierunki).

Funkcja rozkładu Maxwella-Boltzmanna określa liczbę dN cząstek których prędkości zawarte są w przedziale



V, V dV



, a położenia w przedziale



r, rdr



dla przypadku klasycznego (niekwantowego) układu cząstek (np. gazu jednoatomowego lub gazu cząsteczkowego) będącego w równowadze termodynamicznej. Po uśrednieniu prędkości z rozkładu Maxwella-Boltzmanna uzyskuje się rozkład Boltzmanna – funkcję rozkładu ilości cząsteczek w wyróżnionym obszarze. Po scałkowaniu współrzędnych przestrzennych z rozkładu Maxwella-Boltzmanna uzyskuje się rozkład Maxwella – funkcje rozkładu prędkości cząsteczek.

James Clerk Maxwell (1831-1879), szkocki fizyk i matematyk, pierwszy

rozwiązał zagadnienie najbardziej prawdopodobnego rozkładu prędkości wielkiej liczby cząstek gazu doskonałego:

 

_              kT mV V kT m N V N 2 exp 2 4 2 2 2 / 3 0   (1)

gdzie: N

 

V dV jest liczbą cząstek w próbce gazu mających prędkości z przedziału



V, VdV



_,

T jest temperaturą bezwzględną, k jest stała Boltzmana, m jest masą cząsteczki, N jest 0

całkowitą liczbą cząsteczek w próbce

_

 





0

0 N V dV

N .

Charakter rozkładu Maxwella (1), przedstawiony jest na rys.1 dla przypadku , którego tu nie wyprowadzamy, a obejmującego miliona cząsteczek podzielonych na sto przedziałów prędkości. Możemy tam wskazać:

• prędkość najbardziej prawdopodobną Vnp odpowiadającą maksimum funkcji

(przedział numer 24 zawierający 33 866 cząsteczek),

• prędkość średnią Vśr dla której istnieje taka sama liczba cząsteczek poruszających

się szybciej jak i wolniej od niej (przedziały od 1 do 26 zawierają 495 274 cząsteczek,

a przedziały od 1 do 27 zawierają 528 488 cząsteczek).

przedziały prędkosci (v, v+dv) li cz b a cz ą s te cz e k

Rys.1. Charakter rozkładu Maxwella – liczba cząstek dla kolejnych zakresów prędkości.

Prędkości Vnp i Vśr , zależne od temperatury, można wyznaczyć z (1). Prędkość

najbardziej prawdopodobną wyznaczamy szukając maksimum funkcji z warunku zerowania pierwszej pochodnej, w wyniku otrzymujemy:

 

dV kT mV V kT m N dV V N _             2 exp 2 4 2 2 2 / 3 0   (2a)

 

                            kT mV kT mV V kT mV V kT m N dV V N 2 exp 2 exp 2 2 4 2 2 2 2 / 3 0   (2b)

zerowanie się pochodnej jest możliwe tylko wtedy, gdy zeruje się wyrażenie w nawiasie kwadratowym czyli: 0 2 2 exp 2 exp 2 exp 2 2 2 2 2 2                                kT mV V kT mV kT mV kT mV V kT mV V (2c)

Zerowanie się wyrażenia w nawiasie kwadratowym gwarantuje istnienie maksimum funkcji (dla V=0 mamy minimum) stąd prędkość najbardziej prawdopodobna to

m kT m

kT

V_np  2 1,41 (3)

Prędkość średnią wyznaczamy całkując (sumując) prędkości wszystkich cząsteczek i dzieląc otrzymaną prędkość przez liczbę cząsteczek, w wyniku otrzymujemy:

 

_



                 0 2 2 2 / 3 0 0 0 2 exp 2 4 dV kT mV V kT m N dV V N N   (4a) stąd



               0 2 2 2 / 3 2 exp 2 4 1 dV kT mV V m kT   (4b)

chcąc skorzystać ze wzoru na całkę nieoznaczoną typu exp

 

exp

 

₂



1



0  



 ax a ax dx ax x

należy zmienić zmienne. Nowa zmienna i jej różniczka dV

dy V y  2 , 2 nie zmieniają granic całkowania, stąd równanie (4b) przyjmuje postać



                     0 2 / 3 2 2 exp 2 4 1 dy y kT m y m kT   (4c)

po powrocie do pierwotnych zmiennych

                                         1 2 2 2 2 exp 2 4 1 2 2 2 2 / 3 V kT m kT m V kT m m kT   (4d) upraszczając równanie                        1 2 2 exp 8 2 2 V kT m kT mV kT m  (4e)

Ostatecznie prędkość średnia wynosi

m kT m kT V  8 1,59  (5) Wzór barometryczny

Załóżmy, że N cząstek wypełnia naczynie o wysokości H i polu podstawy S. Cząstki te wywierają ciśnienie na ścianki naczynia i ciała znajdujące się wewnątrz, które jest wyższe u podstawy naczynia a niższe na górze p

 

h  p



hdh



. Różnica ciśnień związana z wysokością wynosi dp p



hdh



p

 

h . Przez n(h) oznaczamy

koncentracja cząstek (ilość przypadającą na element objętości). Ilość cząstek w naczyniu na pewnej wysokości to dN n

 

h Sdh, ich masa to dM dNmmn

_{ }

h Sdh, a ich ciężar



mg

  

n h Sdh

dQ  . Cząstki te wywierają ciśnienie

 

hdh mgn S

dQ

dp  (6)

Równanie stanu gazu doskonałego

nRT

pV  (7)

gdzie: n – liczba moli gazu, R stała gazowa.

W stałej objętości (HS) różniczka wyrażenia (7) podstawiona do (6) daje

 

h dh

mgn

skąd dh RT mg n dn   (9) obustronnie całkując

 





h C RT mg h n   ln (10) wyznaczając n(h) mamy

 

 

                         h RT mg C h RT mg C C h RT mg h

n exp exp exp 'exp (11)

Wartość stałej C' znajdziemy z warunku, że wszystkich cząstek w naczyniu jest N

 

_                       

_

_

RT mgH mg RT SC dh h RT mg SC d h n N H exp 1 ' exp ' 0  (12) stąd                RT mgH SRT Nmg C exp 1 ' (13)

Ostatecznie wyrażenie (9) przedstawia zależność średniej koncentracji gazu na wysokości h w polu grawitacyjnym i przyjmuje postać

 

                      h RT mg N RT mgH SRT mg h n exp exp 1 (14)

Zależność ta może też być wyrażona poprzez ciśnienie panujące na wysokości h

 

        h RT mg p h p 0exp (15)

Ilość kulek wyrzucanych z komory i pozostałych w komorze

W układzie laboratoryjnym oprócz wyznaczania rozkładu barometrycznego ciśnienia kulek możemy też wyznaczać ilość kulek, które opuściła komorę przez otwór lub pozostała w komorze. Szybkość ubywania kulek z komory jest proporcjonalna do ich

ilości i zależy od umiejscowienia oraz wielkości otworu. Jeżeli przez dt

dn

oznaczymy szybkość ubywania kulek a przez cn ilość kulek która wyleciała przez otwór (c – pewna stała) to wielkości te muszą być równe:

0   cn

dt

dn ₍₁₆₎

przenosząc człony na dwie strony równania i grupując człony z liczną kulek n po jednej stronie cdt n dn   (17)

Całkując obustronnie od czasu początkowego do końca trwania doświadczenia w dziedzinie ilości zaczynamy od n0 kulek a dochodzimy do n kulek w komorze





 t n n dt c n dn 0 0 (18)

Rozwiązaniami tych całek jest wyrażenie

 

ct n t n           0 ln (19)

z którego wyznaczamy ilość kulek pozostałą w komorze po czasie t

 

t n



ct



n  0exp  (20)

Analogicznie można wyznaczyć ilość kulek, która wypadła przez otwór, a która jest dopełnieniem do ilości kulek z którą rozpoczęliśmy doświadczenie

 

t n





ct





n  ₀1exp  ₍₂₁₎

Wyrażenia (20) i (21) opisują wiele zagadnień w fizyce np. rozpad izotopów, stygnięcie cieczy, ładowanie i rozładowanie kondensatora.