Analiza jakościowa równania opisującego ruch płaski wahadła matematycznego

(1)

Analiza jakościowa równania

opisującego ruch płaski

wahadła matematycznego

Autorzy:

Vsevolod Vladimirov

(2)

(1)

(2)

(3)

Analiza jakościowa równania opisującego ruch płaski wahadła matematycznego

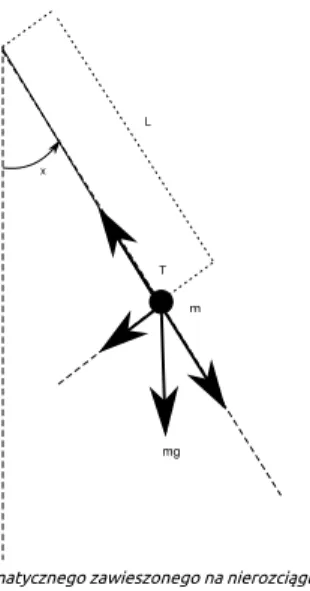
Autor: Vsevolod Vladimirov

Rozpatrzmy model opisujący ruch płaski (czyli dwuwymiarowy) punktu materialnego o masie podwieszonego na nierozciągliwej nici długości w polu grawitacyjnym. Model fizyczny przedstawiony jest na Rys. 1.

mg

T L

m x

Rysunek 1: Model wahadła matematycznego zawieszonego na nierozciągliwej nici w polu grawitacyjnym

Na punkt materialny działa siła grawitacyjna skierowana w dół oraz siła naciągu nici , która w każdej chwili rekompensuje współrzędną podłużną siły grawitacji (warunek nierozciągliwości nici). Siłą wypadkową działającą na punkt materialny jest wówczas składowa poprzeczna siły grawitacji, wynosząca , gdzie oznacza kąt odchylenia nici od pionu. Punkt materialny porusza się wzdłuż okręgu o promieniu ; jego prędkość i przyspieszenie wynoszą odpowiednio i

. Zgodnie z Zasady dynamiki Newtona-Druga zasada dynamiki Newtona, równanie ruchu ma postać

Znak minus w prawej stronie wzoru odzwierciedla to, że siła poprzeczna, skierowana ku położeniu równowagi wahadła przeciwdziała wzrostowi kąta odchylenia.

Napiszmy równanie ruchu w postaci:

W przypadku gdy (relacja oznacza, że wartość bezwzględna jest znacznie mniejsza od jedynki), można zastąpić funkcją . Wówczas otrzymamy dobrze znane równanie liniowe, opisujące małe drgania punktu wokół położenia równowagi:

Ogólne rozwiązanie równania ( 2 ) dane jest wzorem . Poniżej przedstawiamy analizę zbioru rozwiazań równania ( 1 ). Ponieważ rozwiązań tych nie można opisać dokładnie poprzez funkcje elementarne, do ich analizy stosuje się metody jakościowe.

Napiszmy równanie ( 1 ) w postaci równoważnego układu równań rzędu pierwszego:

m,

L,

= m ⋅ g

F

gr

T

m ⋅ g ⋅ sin x

x

L

L (t)

x˙

L (t)

x¨

m ⋅ L ⋅

d2x

= −m ⋅ g ⋅ sin x.

d t2

+

sin x = 0,

ω =

.

x d2 d t2

ω

2

√

− −

g/L

−

|x| << 1

x

sin x

x

+ x = 0,

ω =

.

x d2 d t2

ω

2

√

− −

g/L

−

x(t) = A sin (ωt + ϕ)

= −y,

d x d t

=

sin x.

d y d t

ω

2

(3)

(4)

LEMAT

Lemat 1:

Układ (3) można przepisać w postaci hamiltonowskiej

z funkcją Hamiltona

Dowód

Dowód przeprowadza się bezpośrednim sprawdzeniem.

LEMAT

Lemat 2:

Funkcja Hamiltona układu (3) ma następujące własności: 1.

2. 3.

Dowód

Dowód wynika z niezmienniczości funkcji Hamiltona względem odbić oraz okresowości funkcji . Przypomnijmy sobie, że każdą trajektorię fazową układu hamiltonowskiego można przedstawić w postaci przy pewnej stałej . Trajektorie układu (3) są symetryczne względem odbić od obu osi współrzędnych. Ponadto, na mocy trzeciej własności funkcji , wystarczy przeanalizować przebieg trajektorii fazowych na odcinku i dalej przedłużyć je na kolejne sąsiadujące ze sobą odcinki krotności .

Wszystkie punkty stacjonarne układu (3) leżą na osi poziomej. Współrzędna punktu stacjonarnego należy do zbioru

. Typy poszczególnych punktów stacjonarnych określa zachowanie funkcji

opisującej energię potencjalną układu. Z wykresu tej funkcji, przedstawionego na Rys. 2 odczytujemy że punkty stacjonarne o współrzędnych są środkami, wtedy gdy punkty stacjonarne o współrzędnych są siodłami.

- 4 - 2 2 4 x - 1.0 - 0.5 0.5 1.0 V

Rysunek 2: Wykres energii potencjalnej . Poziomicom niebieskiego koloru odpowiadają rozwiązania okresowe; poziomicy czerwonego koloru - trajektorie heterokliniczne łączące ze sobą punkty siodłowe ; poziomicy leżącej powyżej wykresu funkcji odpowiada ruch nieograniczony.

Fragment portretu fazowego układu (3) jest przedstawiony na .

= −

,

=

.

d x d t ∂ H∂ y d yd t ∂ H∂ x

H(x, y) =

1

−

cos x.

2

y

2

ω

2

H(x, −y) = H(x, y);

H(−x, y) = H(x, y);

H(x ± 2 π, y) = H(x, y).

x → −x, y → −y

cosx

H(x, y) = C,

C

H

(−π, π)

2 π

x

{0, ±π, ±2 π, . . . , ± kπ, . . . } {0, ±π, ±2 π, . . . , ± kπ, . . . } , k ∈ N

V (x) = − cos x,

ω

2

(±2 kπ, 0)

(±(2 k + 1) π, 0)

V(x) = − cos xω2 (± π, 0) V(x)

(4)

- 10 - 5 5 10 x - 2 - 1 1 2 y

Rysunek 3: Portret fazowy układu (3)

Fragmenty, nie pokazane na przedstawionym rysunku, uzyskuje się przeniesieniem portretu odpowiadającego odcinkowi o w lewo i w prawo. Zauważmy że trajektoriom zamkniętym (oznaczonym kolorem niebieskim) odpowiadają nieliniowe rozwiązania okresowe, trajektoriom łączącym siodła (oznaczonym kolorem czerwonym) - rozwiązania heterokliniczneheterokliniczne, trajektoriom leżacym poniżej lub powyżej heteroklinik (oznaczonym kolorem zielonym) - rozwiazania nieograniczone względem współrzędnej .

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 07:31:59

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=2c9b5d09f3b8e5dba181c2c722dc6706

Autor: Vsevolod Vladimirov

(−π, π) 2 π