"Równania stanu w hipotezie skalowania. Zastosowanie do opisu ferroelektryków jednoosiowych"

Instytut Fizyki Jądrowej im. H. Niewodniczańskiego

Polskiej Akademii Nauk

Mirosław Gałązka

RÓWNANIA STANU

W HIPOTEZIE SKALOWANIA.

ZASTOSOWANIE DO OPISU

FERROELEKTRYKÓW

JEDNOOSIOWYCH

Praca doktorska wykonana

w Instytucie Fizyki Jądrowej

im. H. Niewodniczańskiego PAN

pod kierunkiem doc. dr. hab. Piotra Zielińskiego

Kraków 2006

Pragnę gorąco podziękować promotorowi doc. dr. hab. Piotrowi Zielińskiemu

za zaangaŜowanie oraz oferowaną pomoc w czasie pisania niniejszej rozprawy, a takŜe

za czas poświęcony licznym dyskusjom dotyczącym opisu zachowania krytycznego

badanych materiałów.

Podziękowania kieruję takŜe do prof. dr hab. GraŜyny Bator oraz do mgr. Przemysława

Szklarza z Uniwersytetu Wrocławskiego za przeprowadzenie pomiarów, nieocenioną

pomoc i liczne dyskusje, które przyczyniły się do lepszego zrozumienia i interpretacji danych

doświadczalnych oraz za stworzenie miłej atmosfery podczas pobytów we Wrocławiu.

Swoje podziękowania kieruję takŜe do pracowników, koleŜanek i kolegów z Zakładu

Badań Strukturalnych za wszelkie uwagi, cenne rady oraz stworzenie miłej atmosfery.

Dziękuję moim najbliŜszym – rodzicom i rodzeństwu – za cierpliwość i wyrozumiałość jaką

mi okazali.

SPIS TREŚCI

Wstęp

...6

Część I

Teorie zjawisk krytycznych

...11

1. Teoria Landaua...12

2. Przewidywania wynikające z teorii Landaua ...14

2.1. Polaryzacja spontaniczna i wykładnik krytyczny

β

...14

2.2. Podatność w zerowym polu i wykładnik krytyczny

γ

...16

2.3. Izoterma krytyczna i wykładnik krytyczny

δ

...18

2.4. Inne wykładniki krytyczne ...19

3. Ograniczenia teorii Landaua ...22

4. Funkcje termodynamiczne w hipotezie skalowania Widoma ...23

4.1. Własności funkcji jednorodnych ...24

4.2. Relacje między wykładnikami krytycznymi a czynnikami skalującymi ...26

4.3. Relacje pomiędzy wykładnikami krytycznymi ...29

4.4. Skalowanie parametru porządku i podatności ...30

5. Grupa renormalizacji i klasy uniwersalności ...31

6. Kryterium Ginzburga ...32

Część II

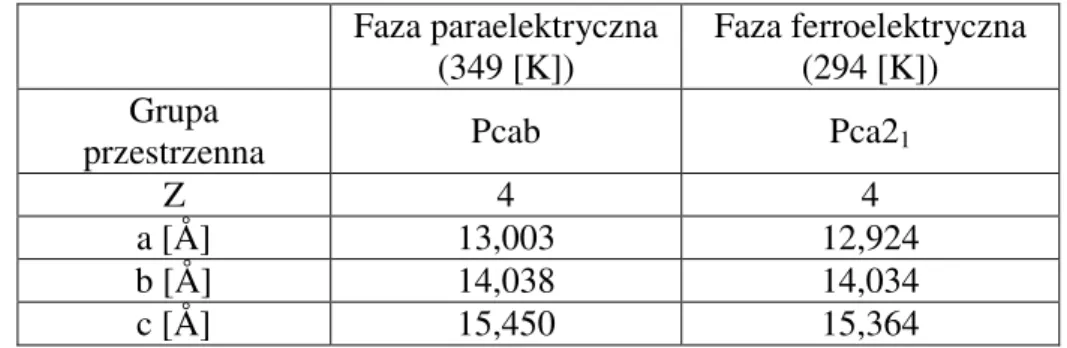
Charakterystyka ferroelektryków MAPCB i MAPBB

oraz wyniki pomiarów spontanicznej polaryzacji

i podatności

...35

7. Ogólne wiadomości o ferroelektrykach MAPCB i MAPBB ...36

8. Piroelektryczne pomiary polaryzacji spontanicznej ...37

9. Nieliniowy efekt dielektryczny ...40

10. Pomiar przenikalności dla zerowego i niezerowego pola odchylającego ...43

10.1. Podatność w zerowym polu odchylającym dla badanych materiałów ...43

10.2. Doświadczalne krzywe NDE oraz skalowanie podatności dla kryształów MAPCB, MAPBB i TGS ...45

10.3. Doświadczalne określenie zakresu stosowalności hipotezy skalowania dla

badanych materiałów ...47

Część III

Równania stanu zgodne z hipotezą skalowania

...51

11. Najprostsze dwuwyrazowe równanie stanu ...52

12. Równanie stanu podane przez Domba ...59

13. Rozszerzenie najprostszego równania stanu: nieliniowa relacja pole – parametr porządku ...67

14. Przegląd moŜliwych uzupełnień równania stanu Domba ...72

15. Najprostsze uzupełnione równanie stanu Domba ...73

16. Niezmienniki skalowania i ich postać w poszczególnych równaniach stanu ...77

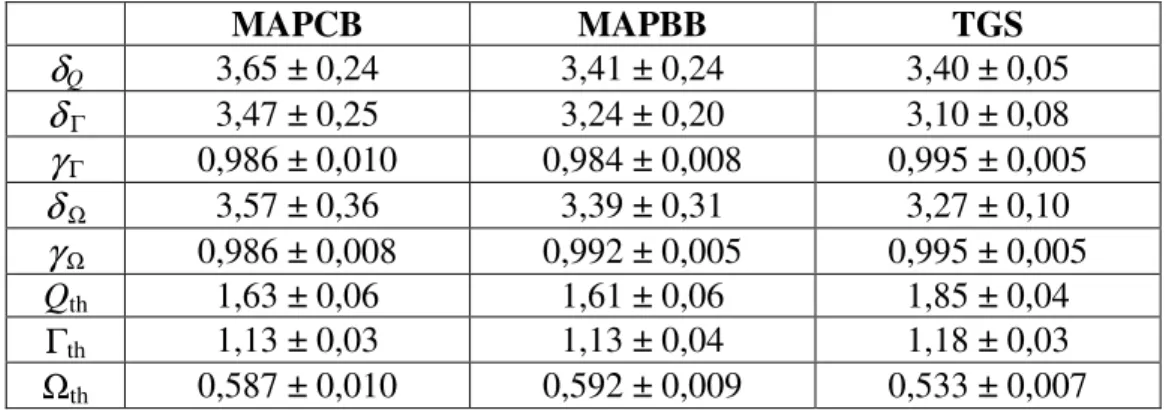
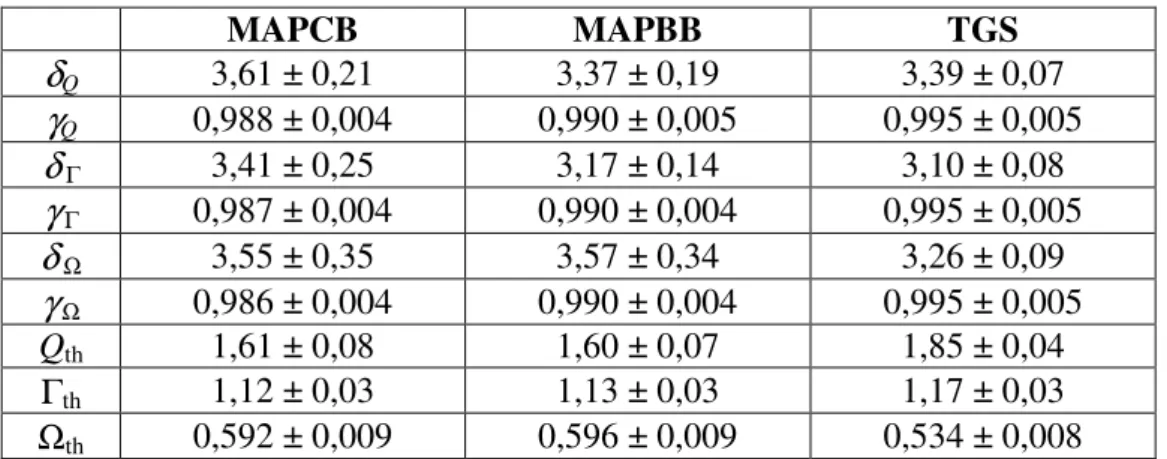
16.1. Definicja niezmienników Q i Γ oraz ich wartości doświadczalne ...77

16.2. Definicja niezmiennika Ω oraz jego wartość doświadczalne ...79

16.3. Jawna postać niezmienników dla najprostszego dwuwyrazowego równania stanu ...81

16.4. Jawna postać niezmienników dla uzupełnionego równania stanu Domba ...84

16.5. Jawna postać niezmienników dla „nieliniowego” równania stanu ...87

16.6. Inne niezmienniki: ogólna postać niezmienników skalowania ...89

17. Dopasowania krzywych podatności dla pól odchylających ...96

18. Ogólne uwagi dotyczące osobliwości w równaniach stanu zgodnych z hipotezą skalowania ...100

18.1. Nieanalityczności w najprostszym dwuwyrazowym i „nieliniowym” równaniu stanu ...101

18.2. Nieanalityczności w równaniu stanu podanym przez Domba ...103

18.3. Nieanalityczności w uzupełnionym równaniu stanu Domba ...103

Podsumowanie teoretyczne opisu zjawisk krytycznych

w ramach hipotezy skalowania

...105

Podsumowanie analizy zachowania krytycznego ferroelektryków

MAPCB, MAPBB i TGS w ramach hipotezy skalowania

...108

Dodatki

Dodatek A. Zastosowanie do opisu zachowania substancji

wyŜszych wyrazów rozwinięcia ...112 Dodatek B. Warunki na punkty przegięcia dla najprostszego równania stanu ...117 Dodatek C. PrzybliŜona postać energii swobodnej wynikająca z równani stanu Domba ..118 Dodatek D. Warunki na punkty przegięcia dla „nieliniowego” równania stanu ...120 Dodatek E. Warunki na punkty przegięcia dla uzupełnionego

dombowskiego równania stanu ...122

Bibliografia

...123

WSTĘP

Przejścia – inaczej przemiany – fazowe są zjawiskami spotykanymi w Ŝyciu codziennym, ale występują równieŜ w bardzo skrajnych warunkach, jakie istnieją tylko w głębokich warstwach skorupy ziemskiej, na odległych ciałach niebieskich, a pojawiały się w kolejnych stadiach rozwoju całego Wszechświata. Zachodzą takŜe w warunkach wytworzonych sztucznie w laboratorium. Z powszednich obserwacji najlepiej znane są zmiany stanu skupienia – parowanie, skraplanie, krzepnięcie, topnienie, sublimacja i resublimacja, czyli przejścia fazowe odpowiednio; fazy ciekłej w gazową, gazowej w ciekłą, ciekłej w stałą, stałej w ciekłą, stałej w gazową i gazowej w stałą. O znaczeniu przejść fazowych w kształtowaniu warunków Ŝycia na Ziemi łatwo się przekonać rozwaŜając obecność róŜnych faz wody w róŜnych biotopach i porach roku. Przejściom fazowym ulegają teŜ substancje wchodzące w skład Ŝywych tkanek, a samo zjawisko przejścia ma niekiedy istotne znaczenie fizjologiczne, na przykład przy transporcie duŜych cząsteczek przez błony komórkowe. Zamiana stanu skupienia metali ze stałego w ciekły i odwrotnie była decydującym czynnikiem rozwoju cywilizacji, poniewaŜ na tym zjawisku opiera się produkcja narzędzi. Parowanie i skraplanie amoniaku w lodówkach pozwala przechowywać Ŝywność przez długi czas. Mimo tak powszechnego występowania, przejścia fazowe są ciągle przedmiotem badań naukowych, które odkrywają coraz to nowe ich właściwości.

Cechą charakterystyczną przejść fazowych jest to, Ŝe są to zjawiska kolektywne, to jest zachodzą one w układach bardzo wielu cząstek, atomów lub cząsteczek chemicznych.

Rząd wielkości wyznacza tu liczba Avogadro N = 6,02214*1023 mol-1. Ogólnie rzecz biorąc

przejścia fazowe zachodzą, gdy zmieniają się parametry opisujące warunki zewnętrzne w jakich znajduje się dany układ. Najczęściej obserwujemy przejścia fazowe pod wpływem zmiany temperatury, ciśnienia, pewnych pól takich jak pole elektryczne albo magnetyczne. To co najbardziej uderza w tych zjawiskach, to nieciągłe zmiany parametrów układu, na przykład gęstości, barwy, namagnesowania, przewodnictwa elektrycznego, róŜnych podatności, itd., w odpowiedzi na ciągłe zmiany warunków zewnętrznych. Nieciągłości mogą dotyczyć róŜnych wielkości fizycznych będących pochodnymi róŜnych rzędów funkcji (potencjałów) termodynamicznych układu: energii wewnętrznej, energii swobodnej, entalpii, entropii swobodnej, itp. Z takich analiz wyrosła znana klasyfikacja przejść fazowych Ehrenfesta [1]. Według niej przejściami fazowymi pierwszego rodzaju są takie przejścia, w których nieciągłości podlega gęstość, entropia, itp., to jest wielkości będące pierwszymi pochodnymi potencjałów termodynamicznych [1-5]. Nieciągłość entropii pociąga za sobą istnienie tak zwanego utajonego ciepło przejścia. Jest to ilość energii jakiej naleŜy układowi dostarczyć (przejście fazowe endotermiczne) albo jaką naleŜy mu odebrać (przejście fazowe egzotermiczne), aby go przeprowadzić z jednej fazy w drugą. Dostarczenie lub odebranie energii (cieplnej) nie zmienia temperatury układu, a tylko wzajemne proporcje róŜnych jego faz. Dzieje się to w stałej temperaturze, zwanej temperaturą współistnienia, albo równowagi faz. Występowanie temperatury współistnienia faz jest drugą po cieple utajonym charakterystyczną cechą wyróŜniającą przejścia fazowe pierwszego rodzaju.

W przejściach fazowych drugiego rodzaju pierwsze pochodne potencjału termodynamicznego są funkcjami ciągłymi parametrów zewnętrznych, za to nieciągłości wykazują drugie pochodne – podatności róŜnego rodzaju i ciepło właściwe. W związku z tym, nie ma ciepła utajonego, ani temperatury, w której obydwie fazy mogłyby współistnieć w równowadze. Dla kaŜdej wartości parametrów zewnętrznych istnieje więc tylko jedna faza

równowagowa, natomiast przekroczenie przez te parametry wartości odpowiadającej przejściu fazowemu objawia się w osobliwości zwanej punktem krytycznym. Punkty krytyczne mogą być izolowane – na przykład w przejściach fazowych pary wodnej w ciecz, gdzie symetria obydwu faz się nie róŜni – albo mogą tworzyć linie lub powierzchnie w przestrzeni parametrów zewnętrznych.

Nieciągłości wyŜszych pochodnych potencjałów termodynamicznych związane są z przejściami fazowymi trzeciego i dalszych rodzajów. Ogólnie przejście fazowe jest n-tego rodzaju, kiedy najniŜszą nieciągłą pochodną potencjału termodynamicznego jest n-ta pochodna. Przejścia fazowe rodzaju trzeciego i wyŜszych występują rzadziej i nie są przedmiotem tej pracy. Makroskopowe własności kaŜdego układu termodynamicznego określa jego równanie stanu, które podaje związki miedzy parametrami zewnętrznymi, a wielkościami charakteryzującymi ten układ.

Celem niniejszej pracy jest skonstruowanie równań stanu, które opisywałyby w sposób ilościowy zachowanie wszystkich wielkości fizycznych charakteryzujących wybrane ferroelektryki jednoosiowe. Jako materiału doświadczalnego uŜyto wyników róŜnych pomiarów wykonanych dla stosunkowo nowych i mało znanych kryształów MAPCB i MAPBB. Dla porównania oraz dla przetestowania zastosowanych procedur doświadczalnych i opisu teoretycznego wykonano kontrolne pomiary i zbudowano analogiczne modele dla bardzo znanego jednoosiowego ferroelektryka TGS. Analiza danych doświadczalnych zarówno dla kryształów MAPCB, MAPBB, jak i TGS wykazała, Ŝe najlepszego schematu konstrukcji równań stanu dostarcza hipoteza skalowania. NaleŜy podkreślić, ze zakresy parametrów zewnętrznych takich jak temperatura T i pole odchylające

E wynikają w tej pracy z typowo przeprowadzanych pomiarów.

Praca została podzielona na trzy części. W pierwszej części przedstawiono istniejące sposoby teoretycznego opisu osobliwości występujących w przejściach fazowych drugiego rodzaju. Część druga przedstawia własności fizykochemiczne badanych materiałów oraz opis technik eksperymentalnych, za których pomocą otrzymano analizowane wyniki. W części trzeciej zawarto konstrukcję poszczególnych wariantów równań stanu zgodnych z hipotezą skalowania oraz porównania tych wariantów z danymi doświadczalnymi. RównieŜ w części trzeciej znajdują się ogólne wnioski dotyczące takich równań stanu: postać niezmienników skalowania, przewidywania pewnych osobliwości poza punktem krytycznym itp. KaŜda część zawiera dokładne wprowadzenie do rozdziałów na jakie została podzielona.

Rozdział 1 streszcza teorię podaną przez Lwa D. Landaua [1-7] dla przejść fazowych drugiego rodzaju. NajwaŜniejszym wynikiem tej teorii jest stwierdzenie, Ŝe linie lub powierzchnie przejść fazowych drugiego rodzaju mogą wystąpić tylko wtedy, gdy symetria jednej z faz dana jest podgrupą symetrii drugiej fazy. Oprócz tego, bazując na rozwinięciach w szereg potęgowy, teoria ta dostarcza przewidywań na temat praw potęgowych rządzących zachowaniem wielkości fizycznych w pobliŜu punktu krytycznego. Przewidywania te wraz z wynikającymi z nich klasycznymi wartościami wykładników krytycznych są omówione w rozdziale 2. W rozdziale 3 zebrane zostały rozbieŜności, jakie istnieją pomiędzy przewidywaniami teorii Landaua, a licznymi danymi doświadczalnymi. Kolejnym krokiem w zrozumieniu opisu zjawisk zachodzących w przejściach fazowych drugiego rodzaju była hipoteza skalowania podana przez Widoma [8] i Griffithsa [9]. ZałoŜenia oraz wnioski wypływające z hipotezy skalowania zostały opisane w rozdziale 4. Wykładniki krytyczne, którym teoria Landaua przypisała określone wartości, a hipoteza skalowania nie określiła ich, są determinowane przez przynaleŜność do jednej z klas uniwersalności wynikających z teorii grupy renormalizacji (R.G.), której krótki zarys został przedstawiony w rozdziale 5. Natomiast w rozdziale 6 omówione zostało kryterium Ginzburga, określające przewidywany zakres parametrów zewnętrznych, w którym naleŜy się spodziewać zachowania krytycznego wynikającego z teorii grupy renormalizacji.

W drugiej części pracy opisane zostały ferroelektryki jednoosiowe MAPCB, MAPBB i TGS. Kryształy MAPCB i MAPBB są stosunkowo nowymi materiałami [10-14]. Ich własności zostały szerzej opisane w rozdziale 7. PoniewaŜ dotychczas zachowanie się w okolicy temperatury krytycznej obydwu ferroelektryków opisane zostało w przybliŜony sposób na gruncie teorii Landaua, dlatego do opisu wybrany został takŜe ferroelektryk TGS, którego własności znane są bardzo dobrze [14-16]. Został on wybrany do „przetestowania” równań stanu podanych w pracy. W rozdziale 8 przedstawione zostały dane z pomiarów

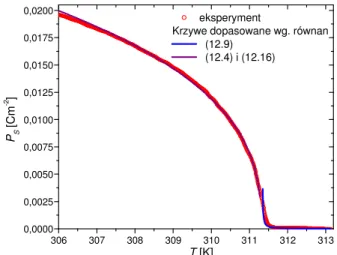
polaryzacji spontanicznej PS(T) dla kryształów MAPCB i MAPBB oraz wyznaczono wartości

wykładnika

β

dla obu materiałów. Poza pomiarami polaryzacji spontanicznej wykonane

zostały pomiary przenikalności

ε

(związanej bezpośrednio z podatnością

χ

) w zaleŜności od przyłoŜonego stałego pola elektrycznego odchylającego (z angielskiego biasing field). Tego rodzaju eksperyment nosi w polskiej literaturze nazwę nieliniowego efektu dielektrycznego (NDE – nonlinear dielectric effect). Rozdział 9 poświęcony został teoretycznym podstawom nieliniowego efektu dielektrycznego oraz opisowi aparatury

słuŜącej do tych pomiarów. Pomiary przenikalności

ε

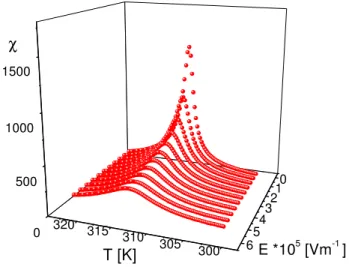
zostały przeprowadzone dla zerowego

i niezerowego pola odchylającego, co zostało przedstawione w rozdziale 10. W podrozdziale 10.2 omówiona została szerzej własność skalowania krzywych podatności

χ

(

τ

,E

)

dla trzech ferroelektryków MAPCB, MAPBB i TGS. W literaturze szeroko znane jest skalowanie namagnesowania (polaryzacji) [1,17,18] oraz podatności w fazie paraelektrycznej (paramagnetycznej) [17-20]. W podrozdziale 10.3 przedstawione zostały uzyskane na podstawie badanych tu danych doświadczalnych zakresy stosowalności hipotezy skalowania dla kryształów MAPCB, MAPBB i TGS równieŜ w fazie ferroelektrycznej. Jak zostało pokazane na rysunkach (14a-c), zakres temperatury, w którym stosuje się hipoteza skalowania w fazie ferroelektrycznej zaleŜy od wartości przyłoŜonego pola odchylającego E. Zakres ten jest potęgową funkcją tego pola. NaleŜy podkreślić, Ŝe otrzymane tu zakresy stosowalności hipotezy skalowania przekraczają przewidywania kryterium Ginzburga.

Trzecia część pracy jest poświęcona poszukiwaniu właściwej postaci równania stanu dla badanych materiałów. Przedstawione zostały róŜne postaci równań stanu. Niektóre z nich (dyskutowane w rozdziale 11 – nazywane najprostszym dwuwyrazowym równaniem stanu i w rozdziale 12 – równanie stanu podane przez Domba) nie dają satysfakcjonującego

wytłumaczenia doświadczalnych wartości ilorazów Γ-/Γ+, czyli nachyleń odwrotności

podatności w zaleŜności od temperatury poniŜej i powyŜej punktu krytycznego w zerowym polu odchylającym. Dlatego w następnych rozdziałach (w rozdziale 13 – równanie stanu wprowadzające nieliniową relację pole – parametr porządku i w rozdziale 15 – uzupełnione dombowskie równanie stanu) przedstawione zostały ich zmodyfikowane formy. Jak wynika ze wzorów na iloraz Γ-/Γ+ moŜe on zaleŜeć nie tylko od wykładników krytycznych (wzór (11.11)) ale od stałych modelu (wzór (15.5)) jak równieŜ od pola mierzącego (wzory (12.20) i (13.9)). Oznacza to, Ŝe wartość ilorazu Γ-/Γ+ wyznaczona na podstawie rozwaŜań teoretycznych moŜe odbiegać od tzw. „landauowskiej dwójki”. Jak wskazują liczne eksperymenty [12,21-26] doświadczalna wartość tego ilorazu dla niektórych substancji silnie zaleŜy od badanych materiałów. MoŜna wśród nich wyróŜnić takie dla których iloraz Γ-/Γ+ jest mniejszy od dwóch i wynosi 0,91 [21], jak równieŜ i takie dla których Γ₋/Γ₊ ≅5,2 [22]. Oznacza to, Ŝe dla wytłumaczenia otrzymywanych, na podstawie danych doświadczalnych, ilorazów Γ-/Γ+ mieszczących się w szerokim zakresie wartości, dla róŜnych substancji, potrzebna jest teoria nie narzucająca na ten iloraz określonej, jednej wartości liczbowej. Takie równania stanu zostały przedstawione w rozdziałach 13 i 15. Równanie stanu zaproponowane przez Domba zostało uzupełnione przez dopisanie kolejnego wyrazu zgodnego z hipoteza skalowania. MoŜliwe ogólne uzupełnienia przedstawione zostały w rozdziale 14. Z równań stanu, opisanych przez funkcje jednorodne, dla podatności

mierzonej w niezerowych polach

χ

(

τ

, ≠E 0

)

wynika istnienie tzw. niezmienników skalowania, które zostały potwierdzone doświadczalnie [16,24,27-30]. Najlepiej opisany w literaturze jest niezmiennik Q [16,24,27,28], związany z punktem maksimum krzywych

(

τ

, ≠E 0

)

χ

. W obecnej pracy zanalizowane zostały dwa nowe niezmienniki – Γ (związany

z punktem przegięcia krzywych

χ

₍

τ

, ≠E 0

₎

) oraz Ω (związany z temperaturami

zredukowanymi) [29,30]. Szerzej niezmienniki skalowania opisane zostały oraz usystematyzowane w rozdziale 16. Dla ferroelektryków MAPCB, MAPBB i TGS przedstawione zostały doświadczalne wartości tych niezmienników. RównieŜ zostały podane ogólne wyraŜenia na te niezmienniki (patrz wzory (16.23) i (16.25)). Jak zostało przedstawione w dalszych podrozdziałach rozdziału 16 istniejącą grupę niezmienników skalowania [16,22,24,27-30] związanych ze szczególnymi punktami krzywych podatności

(

τ

,E

)

χ

, a mianowicie z punktami maksimum i punktami przegięcia, moŜna poszerzyć

o niezmienniki dla dowolnych przeskalowanych temperatur. Dopasowania krzywych teoretycznych

χ

(

τ

, ≠E 0

)

dla kaŜdego równania stanu pokazane zostały w rozdziale 17. W ostatnim rozdziale 18 zawarta została krótka dyskusja dotycząca osobliwości pojawiających się we wszystkich zaproponowanych równaniach stanu. Jak wynika z tej dyskusji, kaŜde równanie stanu posiada pewnego typu nieanalityczności. W pewnych przypadkach osobliwości (patrz podrozdział 18.3) nie mogą zostać udokumentowane doświadczalnie, poniewaŜ wykraczają daleko poza obszar temperatur przebieganych w eksperymencie.

Poszczególne próby skonstruowania równań stanu oraz wnioski z nich wypływające, na przykład wartości niezmienników skalowania, są kaŜdorazowo konfrontowana z danymi doświadczalnymi (rozdziały 11-13, 15, 16.1-16.4, 16.6 i 17).

Głównymi wynikami zawartymi w drugiej i trzeciej części pracy są:

• skonstruowanie zgodnych z hipotezą skalowania, podaną w rozdziale 4, wariantów równań stanu opisujących jednocześnie wyniki pomiarów NDE i ilorazów Γ-/Γ+ w polu zerowym,

• wykrycie moŜliwości uzaleŜnienia ilorazu Γ-/Γ+ od parametrów modelu lub od wartości pola mierzącego w ramach teorii skalowania wzory (11.11), (15.5), (12.20) i (13.9),

• stwierdzenie, Ŝe punkt przegięcia krzywej NDE leŜący w temperaturze niŜszej niŜ maksimum tej krzywej przypada dokładnie w punkcie krytycznym dla wszystkich materiałów opisywanych teorią Landau, z klasycznymi wykładnikami, niezaleŜnie od wartości pola odchylającego,

• wyprowadzenie zaleŜności Pmax(

τ

), Pinf i(

τ

),

χ

max(

τ

),

χ

inf i(

τ

) w punktach maksimum (dolny indeks „max”) i punktach przegięcia (dolny indeks „inf i”) krzywych podatności dla wszystkich równań stanu,

• wykazanie, Ŝe dla niektórych postaci równań stanu istnieją róŜnice pomiędzy wykładnikami krytycznymi dla fazy niskotemperaturowej (ferroelektrycznej, ferromagnetycznej) i wysokotemperaturowej (paraelektrycznej, paramagnetycznej), patrz wzory (12.13) i (12.19) oraz (13.8a) i (13.8b), mimo spełnienia hipotezy skalowania,

• wyznaczenie obszaru stosowalności hipotezy skalowania dla fazy ferroelektrycznej dla MAPCB, MAPBB i TGS (podrozdział 10.2),

• wykrycie potęgowej zaleŜności obszaru stosowalności hipotezy skalowania w fazie

ferroelektrycznej dla badanych materiałów oraz wyznaczenie wykładnika

κ

łączącego

• podanie wzorów na niezmienniki Q, Γ i Ω zaleŜnych od wykładników krytycznych dla wszystkich równań stanu (podrozdziały 16.3-16.5 oraz Dodatki B, D, E),

• podanie ogólnych wzorów na niezmienniki zaleŜne od wartości podatności, niezmienniki DVS, oraz na niezmienniki niezaleŜne od wartości podatności, niezmienniki IVS, jakie mogą być zbudowane na podstawie znajomości połoŜenia danych punktów na krzywych

χ

(

τ

, ≠E 0

)

(podrozdział 16.6),

• poszerzenie klasy niezmienników zaleŜnych od wartości podatności o niezmienniki N

zbudowane dla dowolnych temperatur

τ

> 0 oraz wyznaczenie ich wartości

teoretycznej i doświadczalnej dla ferroelektryków MAPBB i TGS (podrozdział 16.6),

• przedstawienie dopasowań teoretycznych krzywych

χ

(

τ

, ≠E 0

)

dla wszystkich

równań stanu (rozdział 17),

• podanie ogólnych twierdzeń dotyczących osobliwości pojawiających się w równaniach stanu podanych w pracy (rozdział 18) oraz innych równań stanu,

• wykazanie, Ŝe rozszerzenie rozwaŜanego potencjału termodynamicznego rozwiniętego w szereg potęgowy przez dodanie kolejnych wyrazów pozwala uzyskać nieklasyczne wartości wykładników krytycznych, ale jednocześnie nie tłumaczy dokładnie

doświadczalnych wartości ilorazów Γ-/Γ+ dla MAPCB i MAPBB oraz wprowadza

dodatkowe parametry, które naleŜy wyznaczyć z danych doświadczalnych (Dodatek A).

CZĘŚĆ I

TEORIE ZJAWISK KRYTYCZNYCH

Charakterystyczną cechą przejść fazowych drugiego rodzaju jest występowanie punktu krytycznego (temperatury krytycznej TC), w którym wielkości fizyczne takie jak

podatność (elektryczna lub magnetyczna), gęstość albo ściśliwość wykazują osobliwość. Oznacza to niezwykle duŜą czułość materiału na warunki zewnętrzne. WiąŜe się to z powstawaniem fluktuacji o duŜej wartości i szerokiej – w samym punkcie krytycznym nieskończonej – skali przestrzennej. I tak na przykład w temperaturze krytycznej TC dla

mieszaniny cieczy, np. metanolu i heksanu, ściśliwość dąŜy do nieskończoności, natomiast napięcie powierzchowne osiąga zero. Powoduje to powstawanie duŜych fluktuacji gęstości, fluktuacji, których rozmiar jest rzędu długości światła widzialnego [1]. Dlatego roztwór

cieczy podgrzany do temperatury krytycznej TC i następnie oświetlony światłem widzialnym

będzie to światło silnie rozpraszał, dając efekt nieprzezroczystości (mgiełki). Zjawisko to

nazywane jest opalescencją krytyczną. W kryształach podatność

χ

(elektryczna albo

magnetyczna) będzie dąŜyła do nieskończoności, gdy temperatura będzie osiągać TC z obu

stron, natomiast polaryzacja lub namagnesowanie będzie maleć do zera, gdy temperatura

będzie wzrastać do TC. W okolicy temperatury krytycznej powstaną więc fluktuacje

polaryzacji lub namagnesowania. Takie fluktuacje były zaobserwowane pod mikroskopem optycznym [31].

W niniejszej części, poświęconej przeglądowi teorii przejść fazowych drugiego rodzaju, zostały opisane róŜne teorie jakie na przestrzeni przeszło siedemdziesięciu lat zaistniały w tej dziedzinie. W rozdziale 1 przedstawione zostaną załoŜenia teorii podanej przez Lwa D. Landaua. Z tych załoŜeń wynikają pewne prawa potęgowe, rządzące w okolicy przejąć fazowych. Te prawa potęgowe pociągają za sobą wykładniki krytyczne, które zostały zdefiniowane w rozdziale 2. Podane definicje są ogólne i przenoszą się do innych teorii lub hipotez. Teoria podana przez Landaua obok wielu zalet nie opisuje dokładnie wszystkich doświadczeń (między innymi wartości wykładników krytycznych, bądź postaci energii swobodnej), co opisane zostało w rozdziale 3. Te „niedociągnięcia” wynikające z teorii Landaua, pozwoliły wzrosnąć innym hipotezom opisującym przejścia fazowe drugiego rodzaju. Jedną z nich jest hipoteza skalowania Widoma i Griffithsa przedstawiona w rozdziale 4. Hipoteza skalowania nie narzuca na wykładniki krytyczne określonych wartości tak jak teoria Landaua. Jednak wynikają z niej pewne relacje pomiędzy wykładnikami krytycznymi oraz pewne własności funkcji P

(

τ

,E

)

i

χ

(

τ

,E

)

przedstawione w tymŜe rozdziale. Jak zostanie opisane wykładniki krytyczne, nie mogą przyjmować dowolnych wartości. Są one determinowane przez pewne równania skalujące, oraz jednocześnie, co przedstawiają rozdziały 5 i 6 powinny naleŜeć do jednej z klas wynikających z teorii Grupy Renormalizacji.

1. TEORIA LANDAUA

JuŜ pod koniec XIX wieku, w 1895 roku, Pierre Curie [5] odkrył, na podstawie badań tlenu w postaci gazowej oraz niektórych roztworów soli powyŜej temperatury krytycznej, Ŝe podatność

χ

jest odwrotnie proporcjonalna do temperatury bezwzględnej T i wyraŜa się wzorem

χ

= C/T, gdzie C jest stałą Curie. W późniejszym okresie okazało się, Ŝe nie wszystkie substancje paramagnetyczne spełniają prawo Curie. Na początku XX wieku (w 1907 roku) P. Weiss opublikował „poprawione” prawo Curie, obecnie nazywane prawem Curie – Weissa, w postaci

χ

= C/( T –

Θ

), gdzie

Θ

jest pewna stałą dla badanego materiału o wymiarze temperatury. Prawo Curie – Weissa jest spełnione w szerszym zakresie temperatur niŜ prawo Curie. Dla ferromagnetyków

Θ

> 0 (TC <

Θ

, gdzie TC jest temperaturą

Curie lub krytyczną), a dla antyferromagnetyków

Θ

< 0 (TN >

Θ

, gdzie TN jest temperatura

Néela). Prawa Curie i Curie – Weissa podają wzór na zaleŜność podatności

χ

od temperatury

T nie wyjaśniając zachowania się substancji w okolicy temperatury krytycznej. Dopiero w późniejszym okresie XX wieku zaczęły rozwijać się teorie opisujące stan układu w okolicy punktu krytycznego. W latach sześćdziesiątych i siedemdziesiątych ubiegłego wieku powstało wiele prac, które wykorzystując róŜne przybliŜenia matematyczne dąŜyły do podania poprawnego opisu zachowania się funkcji termodynamicznych opisujących stan układu (między innymi energii swobodnej Gibbsa) w okolicy punktu krytycznego. MoŜna do nich zaliczyć prace Domba i Huntera [32], Pokrovskii’ego i Patashinskii’ego [33] oraz Larkina i Khmelnitzkiego [34]. Niewątpliwie jednak najbardziej istotną, jednolitą i dającą jakościowy opis jest teoria podana w 1937 roku przez L. D. Landaua [3,7]. Landau zauwaŜył, Ŝe w przejściach fazowych drugiego rodzaju istnieje związek z symetrią poszczególnych faz, które dla obu faz nie są jednakowe. Przy przejściu z fazy wysokosymetrycznej, najczęściej zwaną fazą paraelektryczną (w ferroelektrykach) lub paramagnetyczną (w ferromagnetykach), do fazy niskosymetrycznej – fazy ferro- (elektrycznej lub magnetycznej) następuje spontaniczne łamanie symetrii, czyli w fazie o niŜszej symetrii „tracone” są pewne elementy symetrii, tak Ŝe grupa symetrii jednej z faz, najczęściej w niŜszej temperaturze, jest podgrupą grupy symetrii drugiej fazy. W skrócie mówimy, Ŝe między tymi fazami zachodzi relacja grupa – podgrupa. Oznacza to, Ŝe w tego typu przejściach fazowych moŜna wyróŜnić wielkość fizyczną, której juŜ infinitezymalnie mała zmiana doprowadza do zmiany symetrii. Tą wielkością jest parametr porządku, którym w ferroelektrykach jest polaryzacja P, a w ferromagnetykach – namagnesowanie M. Parametr porządku, oznaczany dalej literą P, w fazie nieuporządkowanej – o wyŜszej symetrii – musi znikać, natomiast w fazie uporządkowanej – o niŜszej symetrii – musi przybierać wartość róŜną od zera. Łamanie symetrii przy przejściach fazowych drugiego rodzaju, związane z istnieniem parametru porządku, jest jednym z dwóch głównych i najbardziej istotnych spostrzeŜeń dokonanych przez Landaua. Landau załoŜył równieŜ, Ŝe w okolicy punktu krytycznego, energię swobodną Gibssa, F (pomocniczy potencjał termodynamiczny, z języka angielskiego auxiliary), lub odpowiedni potencjał termodynamiczny, odpowiadający warunkom doświadczenia, moŜna rozłoŜyć w szereg potęgowy względem parametru porządku P

(

)

_∑

∞ = = 0 ) ( ; i i i T P F T P F . (1.1)

Wzór (1.1) określa pomocniczy potencjał termodynamiczny. Ma on znaczenie funkcji termodynamicznej tylko dla tych wartości argumentu P, w których przyjmuje on minimum. RozwaŜany potencjał termodynamiczny powinien być niezmienniczy względem grupy

paramagnetycznej). Oznacza to w szczególności, Ŝe przy zamianie P na –P, to jest przy zastosowaniu utraconego elementu symetrii, funkcja F(P ;T ) określona równaniem (1.1) ma być funkcją symetryczną (parzystą). Dlatego potencjał termodynamiczny przyjmuje postać

(

;

)

( ) ( ) ( ) 4 ... 4 2 2 0 + + + = F T F T P F T P T P F . (1.2)

W pobliŜu temperatury krytycznej TC parametr porządku P przyjmuje małe wartości. W

stanie równowagi termodynamicznej potencjał opisujący zachowanie się substancji musi przyjmować minimum. Dlatego w temperaturach wyŜszych od TC, w których P = 0, druga

pochodna F(P;T) względem P jest większa od zera. Natomiast dla temperatur niŜszych od temperatury krytycznej TC, dla których P≠0 nie ma juŜ minimum odpowiadającego fazie

wysokosymetrycznej. Współczynnik F2(T) jest zatem mniejszy od zera. Widać więc,

Ŝe w temperaturze przejścia fazowego, czyli w temperaturze krytycznej, współczynnik F2(T)

zmienia znak. Landau załoŜył, Ŝe i ta zaleŜność moŜne być w pobliŜu TC rozwinięta w szereg

potęgowy względem róŜnicy temperatur. Zatem

F T = a

(

T−TC

)

2 1 ) ( 2 . (1.3a)

Natomiast współczynnik F4(T) w teorii Landaua przejść fazowych drugiego rodzaju jest niezaleŜny od temperatury, więc

0 4 1 ) ( 4 T = b> F . (1.3b)

Oznacza to, Ŝe

(

)

(

)

2 4 0 4 1 2 1 ) ( ;T F T aT T P bP P F = + − _C + . (1.4)

W opisie przejść fazowych drugiego rodzaju wystarczają dwa pierwsze wyrazy z rozwinięcia potencjału termodynamicznego w szereg (1.4). Zdarza się niekiedy, Ŝe w tej samej

temperaturze zeruje się więcej niŜ jeden wyraz Fn. Wówczas mówi się o punkcie

wielokrytycznym. JeŜeli współczynnik F4(T) jest liniową funkcją róŜnicy temperatur,

to znaczy F4(T)= 14b

(

T −TC

)

, wówczas potencjał termodynamiczny z tym współczynnikiem

opisuje punkt trójkrytyczny. Ogólnie więc moŜna rozwaŜać rozwinięcia współczynników Fn

w poniŜszej postaci

∑

∞

(

)

= − = 0 ) ( k k C ik i T f T T F , (1.5)

gdzie i = 2, 4, 6... Wówczas naleŜy na współczynniki fik nałoŜyć pewne ograniczenia [17].

Jednym z nich jest zerowanie się współczynnika f20 oraz dodatnia wartość współczynników

f21 (współczynnik a w zaleŜności (1.3a)) i f40 (współczynnik b w zaleŜności (1.3b)),

co związane jest z faktem, Ŝe dla TC podatność elektryczna lub magnetyczna powinna osiągać

nieskończoność. Dla uproszczenia rozwaŜań oraz dla pokazania zgodności teorii Landaua z przewidywaniami teorii pola średniego (MFT – Mean Field Theory) w dalszych

rozwaŜaniach została obrana forma potencjału termodynamicznego wyraŜonego przez równanie (1.4).

2. PRZEWIDYWANIA WYNIKAJĄCE Z TEORII

LANDAUA

Zgodnie z załoŜeniami teorii Landaua najprostszy pomocniczy potencjał termodynamiczny F opisujący przejście fazowe drugiego rodzaju zadany jest wzorem (1.4). Z jego zaleŜności jako funkcji parametru porządku P oraz temperatury T będą wynikały ściśle określone zaleŜności, które zostaną dokładniej omówione w następnych podrozdziałach.

W podrozdziale 2.1 przedstawiona zostanie zaleŜność polaryzacji spontanicznej PS

(namagnesowania spontanicznego) od temperatury T. Następny podrozdział pokazuje

wynikającą z równania (1.4) zaleŜność

χ

(T) dla pola zerowego. PoniewaŜ potencjał

termodynamiczny F został rozwinięty w szereg potęgowy względem parametru porządku P i do dalszych rozwaŜań wzięte zostały tylko wyrazy do czwartej potęgi w P, dlatego zaleŜności PS i

χ

jako funkcje temperatury T są funkcjami potęgowymi z wykładnikami,

których wartość jest wyraŜona liczbą wymierną, o liczniku i mianowniku będącymi liczbami naturalnymi. W podrozdziale 2.3 przedstawiona została zaleŜność P(E) dla temperatury krytycznej. Ogólnie od podrozdziału 2.1 do podrozdziału 2.4 zostały podane definicje wykładników krytycznych

β

,

γ

,

δ

oraz

α

,

η

i

ν

.

2.1. POLARYZACJA SPONTANICZNA

I WYKŁADNIK KRYTYCZNY

β

β

β

β

RozwaŜając potencjał termodynamiczny zadany równaniem (1.4) widzimy, Ŝe dla temperatur wyŜszych i równych temperaturze krytycznej TC opisany jest on przez funkcję

z jednym minimum globalnym w P = 0. Dla temperatur niŜszych od temperatury krytycznej

TC potencjał termodynamiczny posiada dwa symetryczne względem zera minima globalne

oraz jedno maksimum lokalne w P = 0. Sytuacje te przedstawia rysunek 1.

Zachowanie parametru porządku P w zaleŜności od temperatury przedstawia się następująco [1,2];

(i) w fazie wysokosymetrycznej parametr porządku przyjmuje wartość zero

(minimum potencjału termodynamicznego w zerze), natomiast w fazie niskosymetrycznej parametr porządku przyjmuje wartość niezerową (minima poza zerem),

(ii) parametr porządku dąŜy do zera w sposób ciągły, kiedy temperatura dąŜy

do temperatury krytycznej od strony, gdzie układ posiada niŜszą symetrię (zwykle

od strony temperatur niŜszych od TC). Warunek ten odróŜnia omawiane przejście

fazowe od przejścia fazowego pierwszego rodzaju,

(iii) w fazie niskosymetrycznej parametr porządku przyjmuje jedną z dwóch wartości

S

P

± z równym prawdopodobieństwem (potencjał termodynamiczny F(P;T ) ma

dwa minima; jedno po stronie dodatniej, drugie po ujemnej). Zazwyczaj przyjmuje się te dwie wartości w róŜnych obszarach próbki, tworząc domeny.

-0,006 -0,004 -0,002 0,000 0,002 0,004 0,006 0 2000 4000 6000 F ( P ; T ) [ J m -3 ] P [Cm-2 ] T = 309.0 [K] T = 310.5 [K] T = 311.5 [K] T = 313.0 [K] T = 314.5 [K]

Rys. 1 ZaleŜność potencjału termodynamicznego F (P ;T ) od parametru porządku P dla róŜnych temperatur przy uwzględnieniu wyraŜenia (1.4). Wartości parametrów: a = 7,8*107 _[V2_J-1_mK-1_{], b = 1,6*10}13 _[V4_J-3_m5_]

i TC = 311,5 [K]

Zgodnie z powyŜszymi obserwacjami, wynikającymi z teorii Landaua, termodynamiczna równowaga układu zadana jest przez dwa warunki

=0 ∂ ∂ P F (2.1a) oraz 2 ₂ >0 ∂ ∂ P F . (2.1b)

ZaleŜność (2.1a) jest warunkiem określającym równanie stanu, natomiast równania (2.1a) i (2.1b) są warunkami wystarczającymi i koniecznymi na posiadanie przez funkcję F minimum lokalnego (globalnego).

Z równań (1.4) i (2.1a) wypływa równanie stanu w postaci

(

)

3 0 = + −T P bP T a _C . (2.2)

Z równania (2.2) widać, Ŝe dla T ≥T_C równanie stanu posiada jedno rozwiązanie rzeczywiste

P=0, (2.3a)

natomiast dla T <TC istnieją trzy rozwiązania rzeczywiste

(

)

(

)

1/2 2 , 1 T T b a T T b a P =± _C − =± _C − (2.3b) oraz

P₃ =0. (2.3c) Spontaniczna wartość parametru porządku w fazie niskosymetrycznej (ferro-) opisana jest funkcją potęgową temperatury z wykładnikiem równym ½ – równanie (2.3b), natomiast w fazie wysokosymetrycznej (para-) P = 0. Przejście parametru porządku z fazy ferro- do fazy para- jest więc opisane funkcją ciągłą, co jest zgodne z warunkiem (ii). ZaleŜność spontanicznej wartości parametru porządku przedstawiona jest na rysunku 2.

307 308 309 310 311 312 0,000 0,001 0,002 0,003 0,004 0,005 PS [ C m -2 ] T [K]

Rys. 2 ZaleŜność spontanicznej wartości parametru porządku P(T) zgodnie ze wzorem (2.3b) dla wartości parametrów podanych w opisie rysunku 1

Wykładnik występujący w równaniu (2.3b) i równy ½ jest przykładem wykładnika

krytycznego

β

, który występuje w ogólnym wyraŜeniu

P_S

( )

T = P₀

(

T_C −T

)

β ,dla T →T_C i E =0, (2.4)

gdzie E jest wartością zewnętrznego pola (elektrycznego lub magnetycznego – H) i jest wielkością sprzęŜoną do parametru porządku. W teorii Landaua wykładnik krytyczny

2 1 =

β .

2.2. PODATNOŚĆ W POLU ZEROWYM

I WYKŁADNIK KRYTYCZNY

γγγγ

Aby wyznaczyć podatność (elektryczną lub magnetyczną) w pobliŜu temperatury

krytycznej TC naleŜy uzupełnić wyraŜenie (1.4) o wyraz opisujący oddziaływanie parametru

porządku P z zewnętrznym, sprzęŜonym do niego polem E

F

(

PT E

)

=F T + a

(

T −TC

)

P + bP −EP 4 2 0 4 1 2 1 ) ( , ; . (2.5)

Wówczas równanie stanu opisujące zaleŜność parametru porządku P (polaryzacji lub namagnesowania) od zewnętrznego przyłoŜonego pola E (elektrycznego lub magnetycznego) w temperaturze T przyjmuje postać

(

)

3 bP P T T a E= − _C + . (2.6)

Równanie stanu wynika z zerowania się pierwszej pochodnej potencjału termodynamicznego

F, równanie (2.5), względem parametru porządku P. PrzyłoŜenie pola E wiąŜe się

z wymuszonym łamaniem symetrii (w odróŜnieniu od spontanicznego łamania symetrii w przejściach fazowych drugiego rodzaju). Parametr porządku P w fazie wysokosymetrycznej przyjmuje teraz wartości róŜne od zera, a wzór wyraŜający zaleŜność potencjału termodynamicznego od warunków zewnętrznych, równanie (2.5), nie jest juŜ funkcją symetryczną (parzystą).

Podatność (elektryczna) χ zdefiniowana jest jako szybkość zmiany parametru

porządku P pod wpływem przyłoŜonego pola E S P P E E P = = − _      ∂ ∂ ≡ , 0 1 0 ε χ , (2.7a)

gdzie ε₀ jest przenikalnością elektryczną próŜni 8,85418782 10 12[Fm 1]

0 − − ⋅ = ε .

Dla magnetyków podatność magnetyczna zdefiniowana jest przez wzór (2.7a) bez wielkości

0

ε .

RóŜniczkując równanie (2.6) zgodnie z równaniem (2.7a) otrzymuje się wzór na podatność χ

1

(

(

)

2

)

1 0 3 − − + − =ε aT T_C bP χ . (2.7b)

Podstawiając za P wartości określone równaniami (2.3a) lub (2.3b) dostaje się odpowiednio wyraŜenia na podatność w fazie wysokosymetrycznej (para) lub w fazie niskosymetrycznej (ferro)

( )

(

C

)

para T T a T − = 0 1 ε χ (2.8a) i

( )

(

T T

)

a T C ferro − = 0 2 1 ε χ . (2.8b)

Podatność χ w polu zerowym jest potęgową funkcją temperatury z wykładnikiem krytycznym

–1 dla obu faz. Jest to szczególny przykład wykładnika krytycznego γ, który występuje w bardziej ogólnym i często spotykanym w doświadczeniu wyraŜeniu

±

( )

T =C±T −TC − , dla T →TC i E =0

γ

χ , (2.9)

gdzie dolny indeks „+” odnosi się do fazy para, a „–” do fazy ferro.

=2 − + C C . (2.10a)

Często w literaturze spotyka się określenie ilorazu Γ-/Γ+, które jest odwrotnością zaleŜności występującej po lewej stronie równości w równaniu (2.10a). Wówczas odwrotność podatności zadana jest równaniem

( )

γ χ T =Γ±T −TC − ± 1 _{, (2.10b)} czyli ≡ =2 Γ Γ − + + − C C . (2.10c)

Iloraz nachylenia niskotemperaturowej części odwrotności podatności Γ- do nachylenia wysokotemperaturowej części odwrotności podatności Γ+ zadany wzorami (2.10a) i (2.10c) w teorii Landaua wynosi 2. jest to tak zwana „magiczna dwójka Landaua”.

2.3. IZOTERMA KRYTYCZNA

I WYKŁADNIK KRYTYCZNY

δδδδ

Dla temperatury krytycznej TC równanie stanu (2.6) przechodzi w związek

3

bP

E= .

Wówczas parametr porządku P jest funkcją potęgową przyłoŜonego pola E z wykładnikiem 1/3 3 / 1       = b E P . (2.11)

Mamy tu do czynienia ze szczególnym przypadkiem wykładnika krytycznego δ,

który w ogólnym przypadku charakteryzuje zaleŜność P

( )

E T=T_C

_ci T T_C b E P  =      = , dla / 1 . . δ , (2.12)

2.4. INNE WYKŁADNIKI KRYTYCZNE

Poza wykładnikami krytycznymi β, γ i δ zdefiniowanymi równaniami (2.4), (2.9) i (2.12) istnieją jeszcze trzy inne wykładniki krytyczne: α, η i ν.

Wykładnik krytyczny α łączy zaleŜność ciepła właściwego od temperatury

C

( ) (

T ∝ T −TC

)

− , dla T →TC i E =0

α _{, (2.13)}

gdzie ciepło właściwe C zdefiniowane jest następująco S P P E T F T C = =       ∂ ∂ − ≡ , 0 2 2 . (2.14)

Licząc drugą pochodną potencjału termodynamicznego F zdefiniowanego równaniem (1.4) dla spontanicznej wartości parametru porządku (równania (2.3a) i (2.3b)), otrzymuje się wzory na ciepło właściwe w fazie wysokosymetrycznej

C_para =C₀ (2.15a) i w fazie niskosymetrycznej

( )

T b a C T C_ferro 2 2 0 + = , (2.15b) gdzie 0₂ 2 0 ) ( T T F C ∂ ∂ = .

Ze wzorów (2.15a) i (2.15b) wynika, Ŝe w teorii Landaua wykładnik krytyczny α =0 oraz Ŝe

w temperaturze krytycznej ciepło właściwe C doznaje skoku o wartości

ferro C para C TC b a T C T C C 2 ) ( ) ( 2 = − = ∆ .

Wykładnik krytyczny η wskazuje zaleŜność związanej, dwupunktowej funkcji korelacji (2)

zw

G od odległości r według wzoru

(2)

( )

( 2 )_{, i 0} = = ∝ − − + E T T r r G C d zw η _{, (2.16)}

gdzie d jest wymiarem przestrzeni. Funkcja (2)

zw

G jest miarą stopnia koordynacji parametru porządku w róŜnych punktach [1]. PoniŜej temperatury krytycznej TC, funkcja Gzw

( )

r

) 2

( _{pomija uśrednianie parametru porządku}

w róŜnych miejscach. Wówczas jedynie fluktuacje parametru porządku dają wkład do

( )

r

(2) / , duzeoraz 0 / 1 << − ≠ ∝ − C C r zw e r T T T G ξ & , (2.17)

gdzie ξ jest długością korelacji. Ze wzoru (2.17) wynika, Ŝe poza temperaturą krytyczną parametr porządku fluktuuje w obszarach o rozmiarach liniowych równych bądź mniejszych od długości korelacji ξ. Z dala od temperatury krytycznej TC, zasięg fluktuacji jest niewielki,

natomiast w pobliŜu temperatury krytycznej TC zasięg ten opisywany jest przez wzór

ξ

( )

T ∝T −T_C −ν, T →T_C i E =0, (2.18)

gdzie ν jest szóstym wykładnikiem krytycznym.

Landau rozkładając pomocniczy potencjał termodynamiczny F

(

P;

τ

,E

)

w szereg potęgowy

(2.5) pominął istnienie niejednorodności, czyli zaleŜności parametru porządku od miejsca

w badanym układzie. Daleko od temperatury krytycznej TC występujące niejednorodności są

małe w porównaniu do średniej wartości parametru porządku oznaczanej P , natomiast

w okolicach TC ich wkład staje się niezaniedbywalny. Wówczas w rozwinięciu (2.5) naleŜy

uwzględnić pochodną parametru porządku względem zmiennych przestrzennych. Wówczas

(

)

_∫

( )

[

( )

]

[

( )

]

[

( )

]

( ) ( )

      − ∇ + + + = F a P r bP r c P r E r P r dr E P F ₀ r 2 r 4 r 2 r r r 2 1 4 1 2 1 , ;τ τ τ , (2.19) gdzie τ = T – TC, P

( )

r r

oznacza wartość parametru porządku w punkcie przestrzeni określanej przez wektor wodzący rr, E

( )

rr – wartość natęŜenia pola w punkcie rr oraz ∇P

( )

rr – gradient parametru porządku, czyli niejednorodność parametru porządku. Wzór (2.19) jest wzorem Ginzburga – Landaua.

Minimalizacja potencjału F

(

P;

τ

,E

)

zadanego przez (2.19) jako funkcji parametru porządku

( )

r

P r prowadzi do poniŜszego równania wyraŜającego stan równowagi układu

(

aτ+b

[

P

( )

rr

]

2 −c∇2

)

P

( )

rr =E

( )

rr . (2.20)

Dwupunktowa funkcja korelacji (2)

(

, '

)

r r

G r r zdefiniowana jest przez [2,15]

G(2)

(

rr,rr'

)

=

[

P

( )

rr −P

]

[

P

( )

rr' −P

]

_{, (2.21)}

gdzie P oznacza wartość średnią parametru porządku P≡ P

( )

rr . Jak wynika ze wzoru (2.21) funkcja (2)

₍

, '

₎

r r

G r r opisuje miarę oddziaływania fluktuacji

parametru porządku P

( )

rr – P pomiędzy punktami rr i 'rr . Zakładając niewielką zmianę w natęŜeniu pola E

_{( )}

rr oraz parametru porządku P

( )

rr , czyli zastępując ich wyraŜeniami

E

( )

rr →E

( )

rr +

δ

E

( )

rr (2.22a)

i

moŜna wyznaczyć (2)

₍

, '

₎

r r G r r korzystając z zaleŜności

( )

= 1

_∫

G(2)

(

r,r'

) ( )

E r dr' kT r P r r r δ r r δ , (2.23)

gdzie k jest stałą Boltzmana k = 1,380650*10 -23 [JK-1]. Wzór (2.23) wynika z twierdzenia mechaniki statystycznej [2,15].

Podstawiając za E

( )

rr iP

( )

rr wyraŜenia (2.22a) i (2.22b) do (2.20), pomijając wyrazy

proporcjonalne do

[

( )

]

2

r P r

δ , które są zaniedbywalne, otrzymuje się

(

aτ+3b

[

P

( )

rr

]

2 −c∇2

)

δ P

( )

rr =δE

( )

rr . (2.24)

Za

δ

P

( )

rr występujące we wzorze (2.24) podstawić moŜna (2.23). Wówczas korzystając z dowolności

δ

E

( )

rr otrzyma się

(

3

[

( )

]

2 2

)

(2)

(

, '

)

(

'

)

r r kT r r G c r P b aτ+ r − ∇ r r = δ r−r , (2.25)

gdzie

δ

(

rr−rr'

)

jest deltą Diraca.

Rozwiązanie równania (2.26) ma następującą postać (w trójwymiarowej przestrzeni)

(

)

( )

'

4

'

,

' ) 2 (

r

r

e

c

kT

r

r

G

r r

r

r

r

r

r r

−

=

− − τ ξ

π

, (2.26)

gdzie

ξ

( )

τ

jest długością korelacji zdefiniowaną przez (2.18).

Wzór (2.26) jest rozszerzeniem wzoru (2.17) definiującego dwupunktową funkcję korelacji dla duŜych wartości rr oraz τ ≠0.

Długość korelacji

ξ

( )

τ

występująca we wzorze (2.26) zadana jest przez

( )

2 / 1 2 3      + = bP a c

τ

τ

ξ

. (2.27)

Dla fazy wysokotemperaturowej (paraelektrycznej, paramagnetycznej) P = 0 (patrz wzór (2.3a)) i wówczas

( )

1/2 2 / 1 −       =

τ

τ

ξ

a c para , (2.28a)

natomiast dla fazy niskotemperaturowej (ferroelektrycznej, ferromagnetycznej) P zadane jest przez wzór (2.3b). Wówczas wzór (2.27) moŜna przekształcić do postaci

( )

( )

1/2 2 / 1 2 − −       =

τ

τ

ξ

a c ferro . (2.28b)

porównując wzory (2.28a-b) definiujące zaleŜność długości korelacji

ξ

od temperatury zredukowanej

τ

z definicją wykładnika krytycznego

ν

(2.18) otrzymuje się, Ŝe w teorii Landaua

ν

= ½.

Dla zerowego pola E = 0 i w temperaturze krytycznej T = TC (

τ

= 0) na mocy zaleŜności

(2.28a-b) wzór (2.26) moŜna przekształcić do

(

)

1 0 ) 2 ( _' 4 ' , ₌ = r −r − c kT r r G r r C r r

π

τ . (2.29)

Porównując wzór (2.29) opisujący dwupunktową funkcję korelacji w temperaturze krytycznej TC z definicją wykładnika krytycznego

η

(2.16) otrzymuje się (dla d = 3), Ŝe w teorii Landaua

η

= 0.

Z zaleŜności (2.28a-b) wynika, Ŝe w temperaturze krytycznej, i w jej okolicy, długość korelacji

ξ

( )

τ

dąŜy do nieskończoności. Oznacza to, Ŝe w temperaturze krytycznej TC, cały

układ jest skorelowany. Dlatego teorie, które nie uwzględniają jakichkolwiek fluktuacji parametru porządku (teoria Landaua, teoria pola średniego) nie mogą być stosowane w okolicach temperatury krytycznej TC.

WyraŜenia (2.4), (2.9), (2.12), (2.13), (2.17) i (2.18) pozwalają określić w teorii Landaua wartości wykładników krytycznych, których definicje i wartości zebrane są w tabeli 1.

Wykładnik

krytyczny Definicja Wartość

α

C∝T −TC − ,T →TC,E =0 α 0

β

P∝

(

TC −T

)

,T →TC,E=0 β _½

γ

χ

∝ T−T_C−γ,T →T_C,E=0 1

δ

P∝E ,T =TC / 1δ ₃

η

(2) ∝ −( −2+ ), = , =0 E T T r G C d zw η ₀

ν

ξ

∝T_C −T −ν,T →T_C,E =0 ½ Tabela 1. Definicje i klasyczne wartości wykładników krytycznych

3. OGRANICZENIA TEORII LANDAUA

Teoria Landaua podaje schemat opisu przejść fazowych za pomocą parametru porządku P i będącej jego funkcją pomocniczej energii swobodnej F. Pozwala przewidzieć jakie wyrazy są obecne w tej funkcji na podstawie symetrii. Jednak analityczna postać energii swobodnej, czyli szereg potęgowy względem parametru porządku P, okazuje się niewłaściwą do opisu wielu znanych zjawisk. Dlatego teoria przejść fazowych drugiego rodzaju podana przez Landaua oprócz swojej konsystentnej i prostej budowy posiada następujące wady:

(i) rozwinięcie potencjału termodynamicznego w szereg potęgowy zadany

równaniem (1.4) zakłada, Ŝe wszystkie pochodne cząstkowe F istnieją oraz przyjmują wartości skończone. JednakŜe w dwuwymiarowym modelu Isinga (d = 2) ciepło właściwe opisane jest zaleŜnością logarytmiczną [17,35] w związku z tym posiada osobliwość, której nie da się opisać prawem potęgowym,

(ii) teoria Landaua nakłada na wykładniki krytyczne określone wartości (tabela 1). Z licznych danych doświadczalnych [13,16,19,21,36-40] oraz z róŜnych modeli przejść fazowych (2-d Ising, 3-d Ising, 3-d Heisenberg) otrzymuje się wartości wykładników krytycznych, których róŜnica od wartości klasycznych (landauowskich) leŜy poza granicą błędów pomiarowych,

(iii) wartość ilorazu Γ-/Γ+ przewidziana przez teorię Landaua wynosi 2. JednakŜe

z danych doświadczalnych otrzymywane stosunki Γ-/Γ+ są mniejsze [21,23,41] lub większe [12,16,36,24-26,42] od 2.

(iv) w swojej teorii Landau odrzucił wyrazy odpowiedzialne za fluktuacje parametru

porządku (proporcjonalne do

(

∇P

)

). Oznacza to, Ŝe teoria Landaua nie moŜe być stosowana dla temperatur bliskich temperatury krytycznej TC, gdzie fluktuacje

są znaczące.

Pomimo wad (i)-(iv), wymienionych powyŜej, teoria podana ponad pół wieku temu przez L. D. Landaua jest jednolita, prosta i konsystentna. Pozwala w prosty sposób przewidzieć zaleŜności potęgowe rządzące w okolicy przejść fazowych (np. zaleŜność polaryzacji spontanicznej od temperatury, zaleŜność podatności w zerowym polu od temperatury, itp.). NaleŜy jednak pamiętać, Ŝe rozwinięcie potencjału termodynamicznego określonego równaniem (1.4) w szereg potęgowy względem parametru porządku P pociąga za sobą wymierne wartości wykładników krytycznych. Ponadto, jeśliby w tymŜe rozwinięciu zastosować wyraŜenie (1.5), określające zaleŜność współczynników rozwinięcia potencjału termodynamicznego od temperatury, oraz przyjąć do opisu wyŜsze wyrazy rozwinięcia, tzn. Pn _{dal n > 4, wówczas wartości wykładników krytycznych oraz iloraz Γ}

-/Γ+ naleŜałoby zastąpić pewnymi wartościami efektywnymi. Np. polaryzacja spontaniczna nie byłaby określona prostą zaleŜnością potęgową, równanie (2.3b) lub ogólnie równanie (2.4), lecz naleŜałoby ją zastąpić szeregiem posiadającym wyrazy zaleŜne od róŜnicy temperatur

(

T −TC

)

w róŜnych potęgach. Te róŜnice dałyby jednak o sobie znać dostatecznie daleko od

punkty krytycznego. W Dodatku A przedstawione zostały zaleŜności polaryzacji spontanicznej PS

( )

τ

, ilorazu Γ-/Γ+ oraz efektywne wartości wykładników

β

oraz

γ

- dla

przyjętej energii swobodnej Gibbsa do wyrazu proporcjonalnego do P6.

4. FUNKCJE TERMODYNAMICZNE

W HIPOTEZIE SKALOWANIA WIDOMA

RozbieŜności pomiędzy doświadczalnymi wartościami wykładników krytycznych a tymi przewidzianymi przez teorię Landaua stały się przedmiotem podjętych prób ich wyjaśnienia. Jedną z teorii nie narzucających na wykładniki krytyczne określonych wartości jest hipoteza skalowania Widoma [8], z której dodatkowo wypływają pewne równania

i własności podatności

χ

oraz polaryzacji P (namagnesowania M) omówione szerzej

w poniŜszych podrozdziałach. W podrozdziale 4.1 przedstawione zostały ogólne własności funkcji jednorodnych. Z jednorodnej postaci równania stanu wypływają relacje między wykładnikami krytycznymi a czynnikami skalującymi przedstawione w podrozdziale 4.2, oraz cztery równania skalujące omówione w podrozdziale 4.3. W ostatnim podrozdziale 4.4

wyprowadzone zostaną wzory na skalowania podatności

χ

oraz parametru porządku P

W 1965 roku B. Widom opublikował artykuł dotyczący przejść fazowych drugiego rodzaju w cieczach [8]. ZałoŜył w nim, Ŝe wszystkie funkcje określające równanie stanu są funkcjami jednorodnymi. Zasugerował on, Ŝe w pobliŜu temperatury krytycznej potencjał

termodynamiczny jest funkcją jednorodną zredukowanej temperatury

τ

=T −T_C oraz

zewnętrznego pola E. Oznacza to, Ŝe dla dowolnego większego od zera parametru

λ

istnieją

dwie liczby aT i aE [1,17] takie, Ŝe

F

(

λ

aT

τ

,

λ

aEE

)

=

λ

F

(

τ

,E

)

. (4.1)

Przewidywania hipotezy skalowania nie są tak bardzo restrykcyjne jak te wynikające z teorii Landaua, która na wykładniki krytyczne narzuca określone wartości. Hipoteza skalowania nie prowadzi do określonych wartości wykładników krytycznych, lecz pozwala na sformułowanie czterech relacji skalujących dla sześciu wykładników krytycznych. Oznacza to, Ŝe spośród sześciu wykładników krytycznych jedynie dwa są niezaleŜne. Pozostałe moŜna otrzymać na bazie relacji skalujących.

4.1. WŁASNOŚCI FUNKCJI JEDNORODNYCH

Funkcja n-zmiennych f

(

x1,x2,...,xn

)

jest funkcją jednorodna, jeŜeli dla dowolnej

wartości

λ

spełniona jest następująca relacja [17]

f

(

λ

1x1,

λ

2x2,...,

λ

nxn

)

=g

( )

λ

ˆ f

(

x1,x2,...,xn

)

, (4.2a)

gdzie

λ

ˆ oznacza macierz diagonalną z wartościami

λ

i w i-tym wierszu i i-tej kolumnie.

Punkt (x1,x2,…,xn) n-wymiarowej przestrzeni na bazie której określona jest funkcja f moŜna

zastąpić poprzez n-wymiarowy wektor rr wówczas równanie (4.2a) zostanie zastąpione przez

f

( ) ( )

λ

ˆ =rr g

λ

ˆ f

( )

rr . (4.2b)

W równaniach (4.2a-b) g

( )

λ

ˆ jest pewną funkcją skalarną

λ

ˆ.

Funkcja jednorodna f

( )

rr posiada tę własność, Ŝe jeŜeli znana jest jej wartość f

( )

rr₀ w ustalonym, aczkolwiek dowolnym punkcie przestrzeni rr₀ oraz znana jest postać funkcji,

wówczas znane są wartości funkcji f

( )

rr w dowolnym innym punkcie. Wynika to z równań

(4.2a-b), poniewaŜ kaŜdy punkt n-wymiarowego wektora rr moŜna zapisać jako rr=

λ

ˆrr₀. Funkcja skalująca musi mieć formę

( )

p

g

λ

ˆ =

λ

, (4.2c)

gdzie parametr p nazywany jest stopniem jednorodności lub czynnikiem skalującym,

przy czym ai i / 1

λ

λ

=

.

Jak zostało podane we wprowadzeniu do rozdziału 4 hipoteza skalowania podana przez Widoma operuje na funkcjach określonych dla dwóch zmiennych. Funkcję taką moŜna zapisać w postaci

f

(

λ

axx,

λ

ayy

)

=

λ

f

(

x,y

)

, (4.3)

gdzie ax i ay są dowolnymi liczbami. Funkcja f(x, y) spełniająca relację (4.3) jest z definicji

(4.2a) funkcją jednorodną. ZaleŜność (4.3) jest określona dla dowolnej, dodatniej wartości

parametru

λ

, dlatego wybierając ay

y−1/ =

λ

nie traci się ogólności rozwaŜań. Wówczas

y f

(

x y

)

y x f y y x a a a ,1 , / 1 / − =         . (4.4)

Taki wymiar sprowadza rozwaŜaną funkcję do funkcji efektywnie jednej zmiennej. Funkcja

(

ax/ay ,1

)

xy

f − występująca po lewej stronie równości w (4.4) jest funkcją dwóch zmiennych,

ale druga zmienna jest ustalona i wynosi 1. MoŜna więc ją zastąpić funkcją jednej zmiennej z

F

( )

z ≡ f

( )

z,1 , (4.5)

gdzie ax ay

xy z= − / .

Wówczas na mocy równań (4.4) i (4.5) otrzymuje się

f

(

x,y

)

y1/ayF

( )

z

= . (4.6)

Funkcja f(x, y) z definicji jest funkcją jednorodną i na mocy równania (4.6) moŜe ona być

zapisana jako funkcja F(z) pomnoŜona przez ay

y1/ .

Odwrotnie, jeŜeli funkcję f(x, y) moŜna zapisać w formie (4.6), wówczas funkcja ta jest

funkcją jednorodną. Z równania (4.6) dla dowolnego parametru

λ

wynika następujący

związek

(

) ( )

_       =         = y y y x x x y y y x a a a a a a a a a a y x F y y x F y y x f , 1/ _/

λ

1/ _1/

λ

λ

λ

λ

λ

.

Podstawienie za F(z) zaleŜności (4.6) sprowadza powyŜszą równość do postaci

f

(

λ

axx,

λ

ayy

)

=

λ

f

(

x,y

)

,

czyli funkcja spełniająca równanie (4.3) jest funkcją jednorodną.

W literaturze często moŜna spotkać [1,17,43] postać równania stanu w pobliŜu punktu krytycznego wyraŜoną za pomocą funkcji jednej zmiennej

      = δ

τ

_β / 1 P f P E . (4.7)

Na mocy zaleŜności (4.3) – (4.6) widać, Ŝe powyŜsze równanie stanu (4.7) zapisane jako

jednorodna funkcja jednej, zredukowanej zmiennej _{τ/ P}1/β _{moŜe być rozszerzona}

do równania stanu dwóch zmiennych; zredukowanej temperatury τ i parametru porządku P

JeŜeli f(x, y) jest funkcją jednorodną, wówczas jej pochodna cząstkowa

(

)

f

(

x y

)

y x y x f _k k j j k j, ) _{, ,} ( ∂ ∂ ∂ ∂ = (4.8a)

jest równieŜ funkcją jednorodną

f(j,k)

(

λaxx,λayy

)

=λ1−jax−kay f(j,k)

(

x,y

)

(4.8b)

z czynnikiem skalującym równym 1− ja_x−ka_y [44].

Aby dowieść prawdziwości powyŜszej tezy naleŜy zróŜniczkować obie strony funkcji jednorodnej zdefiniowanej równaniem (4.3) uŜywając równania (4.8a)

λjax+kay f

(

λaxx,λayy

)

₌λ f(j,k)

(

x,y

)

.

Po przekształceniu powyŜsza zaleŜność przyjmuje postać

f(j,k)

(

λaxx,λayy

)

=λ1−jax−kay f(j,k)

(

x,y

)

,

co naleŜało udowodnić.

4.2. RELACJE MIĘDZY WYKŁADNIKAMI

KRYTYCZNYMI A CZYNNIKAMI SKALUJĄCYMI

Potencjał termodynamiczny F w duchu hipotezy skalowania podanej przez Widoma [8] i Griffithsa [9] jest funkcją jednorodną zdefiniowaną równaniem (4.1). Na mocy definicji

parametru porządku P jako funkcji zredukowanej temperatury τ i sprzęŜonego do niego pola

E

(

)

T E F E P       ∂ ∂ ≡ ,

τ

(4.9)

oraz twierdzenia dotyczącego pochodnej funkcji jednorodnej (4.8b) otrzymuje się

P

(

λaTτ,λaEE

)

=λ1−aEP

(

τ,E

)

. (4.10)

Równanie (4.10) jest spełnione dla kaŜdego dowolnego λ>0. Wybierając −1/aT

= τ

λ nie

traci się na ogólności rozwaŜań, poniewaŜ temperatura τ przyjmuje róŜne wartości. Wówczas równanie (4.10) doprowadzić moŜna do postaci

P

( )

E T P

(

E

)

E T E a a a a , , sgn _/

τ

1

τ

τ

τ

− − =         .