Definicja ciągu

(1)

Definicja ciągu

Autorzy:

Katarzyna Czyżewska

(2)

Definicja ciągu

Autor: Katarzyna Czyżewska

Idea ciągu, w różnej formie, towarzyszy każdemu z nas w dniu codziennym. Kolejka do lekarza, układ haseł w encyklopedii, czy cyfry tworzące numer konta bankowego, to wszystko są przykłady ciągów. Widzimy jednak różnicę między ciągiem będącym np. alfabetyczną listą studentów w grupie, a ciągiem, który jest spisem dat w kalendarzu. Jeden z nich jest z konieczności ciągiem skończonym, tzn. posiadającym skończoną liczbę wyrazów, a drugi wydaje się ciągnąć w nieskończoność.

Z matematycznego punktu widzenia układ liczb lub innych obiektów (niekoniecznie matematycznych) tworzy ciąg, jeżeli każdemu elementowi przypiszemy jednoznacznie odpowiadające mu miejsce w ciągu, czyli liczbę naturalną. Najbardziej oczywistym przykładem ciągu liczbowego są liczby naturalne, ponieważ wartość liczby jednocześnie podaje numer miejsca, na którym ona stoi w ciągu.

PRZYKŁAD

Przykład 1: Idea tworzenia ciągu liczbowego

Widzimy, że na każdym miejscu, opisanym przez kolejną liczbę naturalną ustawiamy wyrazy ciągu, które w przykładzie są wielokrotnościami liczby . Procedura taka może oczywiście zatrzymać się w pewnym miejscu, ale może też ciągnąć się w nieskończoność.

DEFINICJA

Definicja 1: Ciąg liczbowy

Ciągiem liczbowym o wyrazach rzeczywistych nazywamy funkcję , która elementom podzbioru zbioru liczb naturalnych ( ) przyporządkowuje liczby rzeczywiste.

UWAGA

Uwaga 1: Oznaczenie ciągu

Wartość ciągu dla argumentu nazywamy -tym wyrazem ciągu i oznaczamy przez dla , natomiast cały ciąg oznaczamy przez , lub w skrócie . Jeżeli mówimy o kilku ciągach jednocześnie, to dla odróżnienia oznaczamy je różnymi literami np. itd.

miejsce w ci

ą

gu:

wyraz ci

ą

gu:

1,

3,

2,

6,

3,

9,

12,

4,

15,

5,

18,

6,

21,

7,

…

3 a : M → R

M

N M ⊂ N

a

n ∈ M

n

a

n

= a(n) ∈ R

n ∈ M

(a

n

)

n∈M

( )

a

n

( ), ( ), …, ( ), ( )

a

n

b

n

x

n

y

n

(3)

DEFINICJA

Definicja 2: Ciąg skończony

Jeżeli dziedzina ciągu jest zbiorem skończonym (np. ), to mówimy, że jest ciągiem skończonym ( -wyrazowym).

PRZYKŁAD

Przykład 2: Skończone ciągi liczbowe

a) jest skończonym -cio wyrazowym ciągiem arytmetycznym o pierwszym wyrazie i różnicy

b) jest ciągiem cyfr w zapisie dwójkowym liczby , czyli jest -wyrazowym ciągiem zero-jedynkowym

c) jest ciągiem kolejnych dwucyfrowych liczb pierwszych, czyli

jest -wyrazowym ciągiem liczb dwucyfrowych

DEFINICJA

Definicja 3: Ciąg nieskończony

Jeżeli dziedzina ciągu jest zbiorem nieskończonym (np. lub zbór liczb parzystych), to mówimy, że jest ciągiem nieskończonym.

PRZYKŁAD

Przykład 3: Nieskończone ciągi liczbowe

a) jest nieskończonym ciągiem geometrycznym o pierwszym wyrazie i ilorazie

b) jest nieskończonym ciągiem pól figur, które tworzymy następująco: w kwadrat o boku wpisujemy koło, w powstałe koło wpisujemy kwadrat, w który wpisujemy kolejne koło itd., czyli

c) jest ciągiem Fibonacciego tzn. dwa pierwsze wyrazy ciągu równe są , a każdy następny jest sumą dwóch wyrazów poprzednich, czyli

M

a

M = {1, 2, …, n}

a

n

( ) = (−8, −3, 2, 7, 12, 17)

a

n

6 −8

5 ( )

b

n

2014

( ) = (1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0)

b

n

11 ( )

c

n

( ) = (11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 91, 97)

c

n

22 M

a

M = N

M =

a

( ) = (1, , , , , …)

a

n 1₃ 1₉ ₂₇1 ₈₁1

1

1₃

( )

b

n

1 ( ) = (1, , , , , , …)

b

n π₄ 1₂ π₈ 1₄ ₁₆π

( )

c

n

1 ( ) = (1, 1, 2, 3, 5, 8, 13, 21, …)

c

n

(4)

UWAGA

Uwaga 2:

Jeżeli dziedzina ciągu nie jest określona jako podzbiór , to przyjmujemy, że jest to cały zbiór .

Komentarz Komentarz

Zgodnie z definicją ciągu możemy podawać ciąg jako funkcję, czyli podać wzór -tego wyrazu ciągu np. w przykładzie Idea

tworzenia ciągu liczbowego wzór na -ty wyraz to , a w przykładzie Nieskończone ciągi liczbowe a) . Zaletą

takiego określenia ciągu jest to, że możemy natychmiast wyliczyć dowolny wyraz ciągu podstawiając do wzoru odpowiednie . Inną z możliwości jest opisanie metody jak należy szukać kolejnych wyrazów ciągu, np. w przykładzie Nieskończone ciągi liczbowe b) szukamy kolejnych figur geometrycznych zgodnie z opisem, a następnie wyliczamy ich pola. Możemy również podać procedurę jak tworzyć kolejne wyrazy ciągu za pomocą wyrazów poprzednich, tzw. procedurę rekurencyjną, należy pamiętać jednak o podaniu wartości odpowiedniej ilości wyrazów początkowych tak, aby procedura mogła wystartować, np. w przykładzie

Nieskończone ciągi liczbowe c) procedurę można opisać następująco

Wadą tej metody określania ciągu jest to, że musimy znać wyrazy poprzednie ciągu, aby wyliczyć wyraz kolejny, co oczywiście jest w praktyce niewygodne, gdy chcemy obliczyć wyraz dla dużego . Kolejną często spotykana metodą zadania ciągu jest podanie kilku jego początkowych wyrazów, tak, aby można było zauważyć schemat tworzenia wyrazów następnych, np. przykład

Nieskończone ciągi liczbowe a), w którym widać, że każdy następny wyraz powstaje z poprzedniego przez przemnożenie go przez . Przy tej metodzie wadą jest to, że należy podać odpowiednio dużo wyrazów początkowych, żeby można było zauważyć schemat, a następnie sprawdzić, czy jest poprawny.

DEFINICJA

Definicja 4: Metody określania ciągu

Podstawowymi metodami określania ciągu są: 1. podanie wzoru na -ty wyraz ciągu, np. 2. podanie wzoru rekurencyjnego, np.

3. opisanie sposobu tworzenia kolejnych wyrazów, np. jest kolejnym wyrazem rozwinięcia dziesiętnego liczby 4. podanie kilku wyrazów początkowych ciągu, aby wiadomo było, według jakiej zasady należy tworzyć wyrazy następne,

np.:

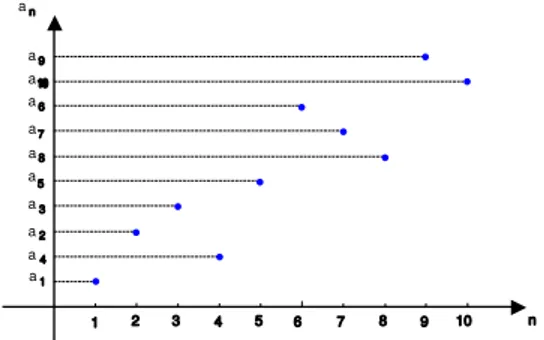
Zgodnie z definicją ciągu, może on być przedstawiony graficznie w postaci wykresu, gdzie na osi odciętych zaznaczamy kolejne liczby naturalne i w układzie współrzędnych zaznaczamy punkty . Widzimy więc, że wykres ciągu składa się z izolowanych punktów w układzie współrzędnych.

M ⊂ N

N

n

a

n

= 3n

a

n

=

₃n−11

n ∈ N

.

⎧

⎩

⎨

⎪

= 1

a

1

= 1

a

2

=

+

, n ≥ 1

a

n+2

a

n

a

n+1

n

1 3

n

a

n

=

1− n+1

, =

2 √[3 (n+3) log3

a

n 6n−8 4+ arcsin(_√ n−2)

{

a

1

= 3

,

= 6– 2 +

a

n+1

a

n

√

− −

1 + a

−−−

n

⎧

⎩

⎨

⎪

= 1

a

1

= 2

a

2

=

a

n+2 an+₂an+1

a

n

√

5 ( ) = ( , , , , …).

a

n 1₂ 2₃ 3₄ 4₅

(n, )

a

n

(5)

a 1 2 3 4 5 6 7 8 9 10 n 1 2 3 4 5 6 7 8 9 10 n a a a a a a a a a a

Rysunek 1: Wykres ciągu składający się z izolowanych punktów w układzie współrzędnych

Wadą takiej graficznej interpretacji ciągu jest to, że zawsze możemy zobaczyć tylko kilka początkowych wyrazów ciągu, czyli w sytuacji, gdy interesować nas będzie zachowanie się ciągu dla bardzo dalekich wyrazów, taka interpretacja jest bezużyteczna. Wygodniej będzie przedstawiać ciąg tylko na osi rzędnych, czyli zrzutować prostopadle punkty reprezentujące wyrazy ciągu na tę oś. Zauważmy, że ten drugi sposób pozwala na umieszczenie na Rys. 1 większej ilości wyrazów ciągu.

DEFINICJA

Definicja 5: Interpretacja geometryczna ciągu

Graficznie ciąg możemy przedstawiać w postaci wykresu funkcji o argumentach naturalnych, otrzymując pełny wykres ciągu lub w postaci rzutu tego wykresu na oś wartości, otrzymując uproszczony wykres ciągu.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 04:52:27

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=5e5f1beb391251d2282e7a55e2e7fd23