Ciąg monotoniczny

(1)

Ciąg monotoniczny

Autorzy:

Katarzyna Czyżewska

(2)

Ciąg monotoniczny

Autor: Katarzyna Czyżewska

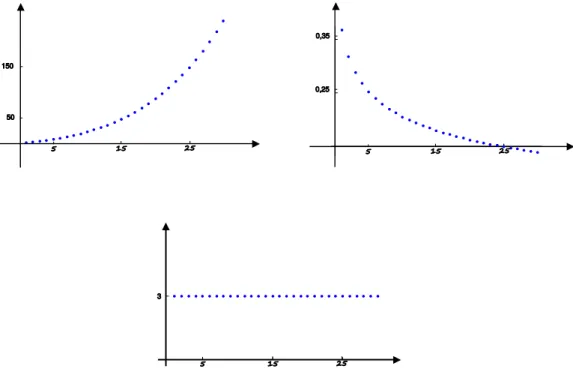
Ciągi, tak jak funkcje, mogą mieć różne własności, których znajomość może przyczynić się do dalszej analizy ich zachowania. Na wykresach ciągów z Rys. 1 widzimy, że charakter każdego z ciągów jest zupełnie inny.

0,35

0,25

3 50

150

Rysunek 1: Wykresy trzech ciągów o różnej monotoniczności

W pierwszym ciągu pokazanym na Rys. 1 każdy kolejny wyraz jest większy od wyrazów poprzednich i ciąg o takiej własności nazywamy rosnącym. W ciągu drugim każdy kolejny wyraz jest od poprzednich mniejszy i ciąg mający taką własność nazywamy malejącym. W trzecim ciągu wszystkie wyrazy są takie same i taki ciąg nazywamy stałym. Może się również zdarzyć, że każdy kolejny wyraz ciągu jest nie mniejszy albo nie większy (tzn. może być też równy) od wyrazu poprzedniego i ciągi o takich własnościach nazywamy niemalejącym albo nierosnącym. Zauważmy, że ciąg stały jest jednocześnie niemalejący i nierosnący. Istnieją oczywiście ciągi, które nie są ani rosnące lub niemalejące, ani malejące lub nierosnące, ani stałe i mówimy, że taki ciąg nie jest monotoniczny. Rys. 2 przedstawia ciąg, który nie ma żadnej z powyższych własności.

Rysunek 2: Wykres ciągu, który nie jest ciągiem monotonicznym

Rzeczywiście, np. wyraz drugi jest większy od wyrazu pierwszego, wyraz trzeci jest natomiast mniejszy od drugiego, wyraz czwarty jest znowu większy od trzeciego itp.

(3)

DEFINICJA

Definicja 1: Ciąg rosnący

Mówimy, że ciąg jest rosnący, jeżeli dla wszystkich spełniona jest nierówność .

DEFINICJA

Definicja 2: Ciąg malejący

Mówimy, że ciąg jest malejący, jeżeli dla wszystkich spełniona jest nierówność .

DEFINICJA

Definicja 3: Ciąg stały

Mówimy, że ciąg jest stały, jeżeli dla wszystkich spełniona jest równość .

DEFINICJA

Definicja 4: Ciąg niemalejący

Mówimy, że ciąg jest niemalejący, jeżeli dla wszystkich spełniona jest nierówność .

DEFINICJA

Definicja 5: Ciąg nierosnący

Mówimy, że ciąg jest nierosnący, jeżeli dla wszystkich spełniona jest nierówność .

UWAGA

Uwaga 1:

Jeżeli ciąg posiada jedną z wyżej wymienionych własności w całej swojej dziedzinie, to nazywamy go ciągiem monotonicznym. Komentarz Komentarz

(a

n

)

n∈M

n ∈ M

a

n+1

>

a

n

(a

n

)

n∈M

n ∈ M

a

n+1

<

a

n

(a

n

)

n∈M

n ∈ M

a

n+1

=

a

n

(a

n

)

n∈M

n ∈ M

a

n+1

≥

a

n

(a

n

)

n∈M

n ∈ M

a

n+1

≤

a

n

(4)

Definicję Ciąg rosnący można w sposób równoważny wyrazić w postaci nierówności , która powinna być spełniona dla każdego . Jeżeli dodatkowo wiemy, że wszystkie wyrazy ciągu są dodatnie, to ciąg jest rosnący, gdy dla wszystkich spełniona jest nierówność . Jeżeli w nierównościach zmienimy zwroty nierówności na przeciwne, to analogiczne warunki równoważne definiują ciąg malejący. Wypisane warunki są łatwiejsze do sprawdzenia w praktyce, gdyż wystarczy zbadać znak różnicy lub dla ciągów o wyrazach dodatnich przyrównać iloraz do jedynki, aby odpowiedzieć na pytanie o monotoniczność ciągu.

PRZYKŁAD

Przykład 1:

Zbadaj monotoniczność ciągu Rozwiązanie

Rozwiązanie

Zbadamy znak różnicy .

dla

Widzimy, że różnica jest dodatnia dla wszystkich .

Wykazaliśmy, że ciąg jest rosnący.

PRZYKŁAD

Przykład 2:

Zbadaj monotoniczność ciągu Rozwiązanie

Rozwiązanie

Zauważamy, że wszystkie wyrazy ciągu są dodatnie, więc obliczamy iloraz .

Iloraz jest mniejszy od jedynki dla wszystkich .

Wykazaliśmy, że ciąg jest malejący.

−

> 0

a

n+1

a

n

n ∈ M

(a

n

)

n∈M

n ∈ M

an+1

> 1

an

−

a

n+1

a

n a_an+1_n

=

, n ∈ N

a

n 3n−1_n+3

−

a

n+1

a

n

−

=

−

=

> 0

a

n+1

a

n 3n+2_n+4 3n−1_n+3 (3n+2)(n+3)−(3n−1)(n+4)_(n+4)(n+3) _(n+4)(n+3)10

n ∈ N

−

a

n+1

a

n

n ∈ N

(a

n

)

n∈N

= , n ∈ N

b

n ₂1n bn+1 bn

=

∶

=

⋅

= < 1.

bn+1 bn 1 2n+1 ₂1n ₂n+11

2

n 1₂ bn+1 bn

n ∈ N

(b

n

)

n∈N

(5)

PRZYKŁAD

Przykład 3:

Zbadaj monotoniczność ciągu .

Rozwiązanie Rozwiązanie

Określimy znak różnicy dla wszystkich .

dla

Obliczamy jeszcze i i zauważamy, że .

Wykazaliśmy, że różnica jest dodatnia dla wszystkich , czyli ciąg jest rosnący.

Komentarz Komentarz

Bardzo często analiza zachowania się ciągu liczbowego sprowadza się do badania zachowania się tego ciągu dla wyrazów o dużych indeksach, czyli nie interesuje nas zachowanie się początkowych wyrazów ciągu (nawet dużej ich ilości), a raczej „końcówka” tego ciągu. Z takiego punktu widzenia, może się zdarzyć, że dopiero po odrzuceniu pewnej liczby wyrazów początkowych, otrzymujemy ciąg monotoniczny i takie ciągi nazywamy monotonicznymi od pewnego miejsca.

0,3 0,1 -0,1 5 15 25 2 1 -1 5 15 25 25 15 5 0,5 1,5

Rysunek 3: Wykresy trzech ciągów, których monotoniczność ustala się dopiero od pewnego wyrazu

Rys. 3 przedstawia wykresy trzech ciągów, których monotoniczność ustala się dopiero od pewnego wyrazu, a nie od wyrazu pierwszego, jak to ma miejsce dla ciągów monotonicznych. Rzeczywiście pierwszy wykres przedstawia ciąg, który jest rosnący począwszy od 11-go wyrazu. Drugi wykres przedstawia ciąg, który jest malejący począwszy od 8-go wyrazu, a wykres trzeci przedstawia ciąg, który jest stały od 16-go wyrazu.

=

, n ≥ 2

c

n

√

n

−

−−−−

2

− 2n

−

c

n+1

c

n

n ≥ 2

− =

−

= (

−

) ⋅

=

c

n+1

c

n

√

(n + 1 − 2(n + 1)

−

−−−−−−−−−−−−−

)

2

−

√

−

n

−−−−

2

− 2n

−

√

− −

n

−−−

2

− 1

√

−

n

−−−−

2

− 2n

−

√_√_nn22−1₋₁+₊_√√n_n22_−2n−2n n−1− +2n 2 _n2 + −1 n2 √ _√n2−2n

=

2n−1

> 0

+ −1 n2 √ _√n2−2n

n ≥ 3.

=

c

3

√

3 c

2

= 0

c

3

− > 0

c

2

−

c

n+1

c

n

n ≥ 2

(c

n

)

n≥2

(6)

DEFINICJA

Definicja 6: Ciąg rosnący od pewnego miejsca

Jeżeli dziedziną ciągu jest i istnieje takie, że dla każdego spełniona jest nierówność , to

mówimy, że ciąg jest rosnący od pewnego miejsca.

DEFINICJA

Definicja 7: Ciąg malejący od pewnego miejsca

Jeżeli dziedziną ciągu jest i istnieje takie, że dla każdego spełniona jest nierówność , to

mówimy, że ciąg jest malejący od pewnego miejsca.

DEFINICJA

Definicja 8: Ciąg stały od pewnego miejsca

Jeżeli dziedziną ciągu jest i istnieje takie, że dla każdego spełniona jest równość , to

mówimy, że ciąg jest stały od pewnego miejsca.

PRZYKŁAD

Przykład 4:

Dziedziną ciągu jest zbiór . Badamy znak różnicy .

dla .

Widzimy, że różnica jest dodatnia tylko dla , czyli ciąg jest rosnący od 3-go miejsca.

( )

a

n

N

n

0

∈ N

n ≥ n

0

a

n+1

>

a

n

( )

a

n

N

n

0

∈ N

n ≥ n

0

a

n+1

<

a

n

( )

a

n

N

n

0

∈ N

n ≥ n

0

a

n+1

=

a

n

=

− 6n + 8

a

n

2

N

a

n+1

−

a

n

−

= (n + 1 − 6(n + 1) + 8 − ( − 6n + 8) = 2n − 5 > 0

a

n+1

a

n

)

2

n

2

n >

5₂

−

a

n+1

a

n

n >

5₂

(a

n

)

n∈N

(7)

PRZYKŁAD

Przykład 5:

Dziedziną ciągu jest zbiór . Badamy znak różnicy .

dla .

Widzimy, że różnica jest ujemna tylko dla , czyli ciąg jest malejący od 5-go miejsca.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 04:53:27

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=a7ef7678fa0e3ab10ab7814adc17d3e2