Podstawy teorii plastycznoci

9.

9. PODSTAWY TEORII PLASTYCZNOŚCI

9.1. Pierwsze kroki

Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co będzie się działo z materiałem po przekroczeniu pewnych odkształceń odwracalnych czyli tzw. sprężystych.

W tym wykładzie postaramy się krótko omówić podstawowy teorii plastyczności. Będziemy tu analizować zatem stan, kiedy przekroczone zostaną odkształcenia sprężyste. Pojawią się odkształcenia nieodwracalne nazywane plastycznymi.

Do analizy materiału plastycznego wprowadzamy naprężenia _ij, prędkości czyli przyrosty przemieszczeń opisywane jako ˙u_i oraz prędkości odkształceń plastycznych, które występują podczas plastycznego płynięcia oznaczane przez ˙_ijP.

W teorii ciał idealnie plastycznych definiujemy plastyczne płynięcie jako proces, w którym

naprężenia nie zależą od skali czasu. Oznacza to, że np. podczas przeprowadzenia prób jednoosiowego

rozciągania, przeprowadzonych z różnymi prędkościami odkształceń, wartości naprężeń będą niezmienne i będą przyjmowały wartości granicy plastyczności. Wynika z tego, że pojawienie się deformacji plastycznych jest uwarunkowane spełnieniem zależności:

F

=0

(9.1)

Jeżeli ponadto przyjmiemy założenie, że

∂

ij

∂ ˙

kl P

=

∂

kl

∂ ˙

ij P (9.2)

które z całą pewnością spełnione będzie dla materiałów izotropowych, będziemy mogli wykazać, że prędkości odkształceń plastycznych zostaną wyrażone przez tzw. stowarzyszone prawo płynięcia, które można zapisać następująco

˙

ij P

= ˙

∂

kl

∂ ˙

ij

P (9.3)

Równość (9.3) pokazuje nam, że wektor prędkości odkształceń plastycznych jest prostopadły do powierzchni opisanej przez warunek plastyczności. Graficznie możemy to przedstawić następująco

Rys. 9.1. Graficzne przedstawienie stowarzyszenia

Stowarzyszenie polega na tym, że funkcja

F



odgrywa rolę potencjału dla prędkości odkształceń plastycznych

_˙

. Przestawione równanie (9.3) wiąże nam naprężenia z prędkościami odkształceń, ma więc sens równania fizycznego dla ciał plastycznych

Jednym z ograniczeń na warunek plastyczności, jest wniosek z tzw. postulatu Druckera. Zgodnie z tym postulatem przyrost pracy wykonanej w cyklu naprężeniowym na nieskończenie małym przyroście odkształcenia jest nieujemny.

Sens postulatu przedstawimy na przykładzie materiału sprężysto-plastycznego ze wzmocnieniem liniowym dla jednoosiowego przypadku obciążenia i odciążenia. Przyjmijmy, że naprężenie

_

odpowiada punktowi należącemu do powierzchni plastyczności tzn. wymagane jest spełnienie warunku (9.1). Ponadto załóżmy naprężenie

 '

, które będzie odpowiadać dowolnemu stanowi dopuszczalnemu, a więc takiemu który leży wewnątrz lub na powierzchni plastyczności, czyli spełniającego warunek

F

0

. Dodajmy jeszcze, że symbolem

d



oznaczono infinitezymalny przyrost naprężenia,

d



E_{- przyrost odkształceń}

sprężystych,

d



P_{- przyrost odkształceń plastycznych, które zostały wywołane przez}

_d

_

_. _II

_I ˙_pl

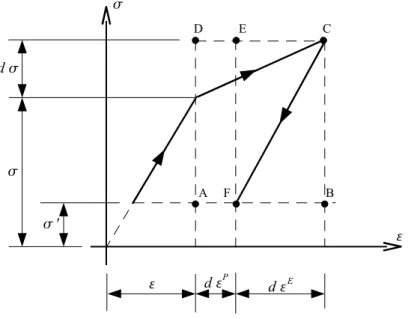
Rys. 9.2. Wykres

−

dla jednoosiowego przypadku obciążenia i odciążenia materiału sprężysto-plastycznego ze wzmocnieniem liniowym

Z rysunku (Rys. 9.2.) widać, pole prostokąta BCEF jest nie większe od pola prostokąta ABCD. Możemy to zapisać



− 'd 





d



E

d 

P



−



− 'd 



d



E

0

(9.4)

Jeśli zredukujemy wyrazy podobne otrzymamy



− '



d



P

d  d 

P

0

(9.5)

Jeśli weźmiemy pod uwagę fakt, że wyrażenie

d

 d 

P _{jest małą wartością wyższego rzędu i}

przyjmiemy, że możemy je pominąć dostaniemy



− '



d



P

0

(9.6)

lub inaczej

 d 

P

 d 

P _(9.7)

Nierówność (9.7) jest prawdziwa zarówno dla materiałów idealnie plastycznych, jak i dla materiałów ze wzmocnieniem plastycznym. d   ' D E C A F B    dP dE

Jeśli przyjmiemy, że będziemy potrafili znaleźć plastyczną i sprężystą część odkształceń wówczas będziemy mogli określić całkowite odkształcenia ze wzoru:

=





pl _(9.8)

gdzie =

E to część sprężysta odkształcenia, a pl stanowi część plastyczną odkształcenia

Jak możemy wywnioskować z wcześniejszych rozważać dotyczących teorii plastyczności warunek plastyczności jest nieliniową funkcją składowych stanu naprężenia np. warunek H-M-H (przejście cząstki materiału w stan plastyczny następuje z chwilą osiągnięcia przez jednostkową energię odkształcenia postaciowego pewnej wartości krytycznej). Spełnienie warunku plastyczności świadczy o tym, że plastyczne płynięcie może wystąpić. Nie jest jednak ono bliżej określone - jak przebiega ruch plastyczny, czyli jak narastają składowe tensora odkształcenia. Te informacje zawiera prawo plastycznego płynięcia wiążące przyrosty odkształceń plastycznych z naprężeniami lub prędkości odkształcenia plastycznego

_

˙

pl _z

naprężeniami. Czyli do określonego stanu naprężenia, spełniającego warunki plastyczności, wektor prędkości odkształceń plastycznych ma kierunek normalnej do powierzchni – mamy tu na myśli przedstawione wcześniej stowarzyszone prawo płynięcia.

Dla przykładu podajmy, że beton należy do materiałów niestowarzyszonych plastycznie, natomiast materiały ciągliwe zaliczamy do stowarzyszonych plastycznie (zależą od drugiego niezmiennika)

Algorytm analizy plastycznej MES wymaga:

• sformułowania standardowej macierzy sztywności stycznej układu

• sformułowania macierzy konsystentnej do procedur iteracyjnych np. Newtona-Raphsona

• całkowanie związków konstytutywnych celem zmodyfikowania tensora naprężeń



dla odksztalceń

nieliniowych

Przeanalizujmy następujące zadanie Mamy belkę pokazaną na rysunku poniżej

Zauważmy, że jeśli belkę obciążymy siłą skupioną, inaczej będą wyglądały odkształcenia w punkcie A a inaczej w punkcie B.

Na początku włókna w punkcie A będą ściskane, ale po osiągnięciu granicy plastyczności zaczną ulegać rozciąganiu. Natomiast włókna w punkcie B będą cały czas rozciągane. Przebieg odkształceń we

A

B P

włóknach w punktach A i B pokazano na wykresie poniżej  ₀ −₀  A B ₀

Moment, w którym zarówno we włóknach górnych jak i dolnych będą takie same co do wartości i znaku wartość naprężeń nastąpi wówczas, gdy wielkość przemieszczeń osiągnie wartość równą



0

=d

(9.9)

gdzie d jest wysokością przekroju belki

9.2. Nieliniowości fizyczne

9.2.1. Przyczyny nieliniowości leżące w istocie związku konstytutywnego

Warunek plastyczności (warunek Hubera):

I_z−k0 2

=0 (9.10)

gdzie k0 oznacza wartość graniczną plastyczności. Warunek ten jest obrazem używanego przez nas zastępczego naprężenia:



x2 3xy2

Omawianą tu plastyczność rozważać będziemy na poziomie: 1) punktu,

2) przekroju, 3) konstrukcji.

9.2.2. Plastyczność na poziomie punktu.

Znany jest nam stan naprężeń punktu {σ}, jednak istotę stanowi znalezienie stanu naprężeń w każdym punkcie. Rozważmy najpierw zachowanie materiałów nieciągliwych, kruchych.

• warunek plastyczności dla betonu:

W stanie plastycznym, po przekroczeniu pewnej granicy, mimo odciążania pozostaną trwałe odkształcenia (oznaczone na rysunku jako εpl):

σ ε ε_pl σ₂ σ₁ interpretacja graficzna warunku plastyczności dla betonu

• w przypadku rozciągania omawianych materiałów pojawiają się geometryczne nieliniowości. Stan plastyczny możemy jednak sprowadzić do jednego punktu.

Dla materiałów ciągliwych wyróżniamy dwa typy wzmocnienia:

a) wzmocnienie izotropowe – w wyniku kolejnej deformacji równowagę stanu naprężenia można uchwycić na rosnącym wzmocnieniu.

Warunek plastyczności Hubera dla materiałów ciągliwych:

Prezentowane na rysunku wzmocnienie izotropowe jest obrazem rzutu przestrzennego walca, mającego przekątną nachyloną do wszystkich osi pod tym samym kątem. Wprowadza ono dla materiałów ciągliwych stan quasistatyczny:

=spl (9.12)

gdzie εs – odkształcenie sprężyste, εpl – odkształcenie plastyczne.

Wzmocnienie izotropowe pozwala nam na znajdowanie stanu plastycznego tylko w obrębie jego powierzchni. σ₂ σ₁ izotropowe wzmocnienie wg hipotezy Treski wg teorii Hubera

b) wzmocnienie kinematyczne – w tym przypadku możemy zaobserwować efekt histerezy:

Opiszmy ewolucję tensora resztkowego jako {α}. Wówczas dla wzmocnienia kinematycznego możemy zapisać teorię plastyczności

Iz{}−{} (9.13)

Zakładając {α}={0}, {k}={0} otrzymamy stan idealnie plastyczny.

Obiektywną miarą dla porównania stanów naprężeń (na przykład w dwóch różnych punktach) będzie energia. Przyjmijmy, że znamy stan naprężeń w pierwszym punkcie σ1. Możemy σ1 rozłożyć na aksjator i dewiator:

1=1A

1D _(9.14)

Identycznie postąpimy z tensorem naprężeń dla drugiego punktu:

2=2A 2 D _(9.15) σ ε σ₂ σ₁

obciążenie dalej jest przenoszone, powierzchnia

ewoluuje

tensor resztkowy odciążenie obciążenie

Teraz możemy zamienić powyższe tensory na energię:

9.2.3. Plastyczność na poziomie przekroju

Plastyczność na poziomie przekroju możemy omówić na przykładzie symetrycznej belki (przekroju płaskiego). Wstępne wykresy naprężeń i odkształceń przybierają postać:

Jeśli zdecydujemy się na dalsze odkształcanie belki, to otrzymamy wykres

E EA dla punktu 1 ED E EA dla punktu 2 ED

tylko ta część (energia postaciowa) odpowiada za stan plastyczny

σ_x ε

M

σ₀

σ0 oznacza tu naprężenie sprężyste graniczne. Odkształcenia na tym etapie również są sprężyste, podobnie jak moment w przekroju, który możemy wyznaczyć ze wzoru:

M₀=0

bh2

6 (9.16)

Odkształcając dalej:

Ostatnim etapem jest sytuacja, gdy cały przekrój zostaje uplastyczniony:

σ₀ σ₀ cały przekrój uplastyczniony σ₀

odkształcenie ma tutaj charakter stały σ₀

część sprężysta

Moment w tym przekroju obliczymy ze wzoru

Mpl=0bh 2

4 (9.17)

9.2.4. Plastyczność na poziomie konstrukcji.

Plastyczność na poziomie konstrukcji wyrazimy w obciążeniach:

Analiza plastyczna MES wymaga:

• sformułowania standardowej macierzy sztywności stycznej układu,

• sformułowania macierzy konsystentnej do procedur iteracyjnych N-R,

• całkowania związków konstytutywnych, aby zmodyfikować stan naprężeń.

Dla materiałów nieliniowych:

Kt=

∫

V BT_D tB dVKNLd  (9.18) V H V H powstanie mechanizmu belkowego l l l

gdzie

Dt= ∂

∂ (9.19)

Dokonamy teraz uaktualnienia naprężeń w punkcie Gaussa:

• odkształcenia iteracyjne 1) Obliczamy ∂ d :

∂ d =−kt

−1_{⋅r (9.20)}

2) Na podstawie wzoru 9.20 wyznaczamy ∂:

∂= f ∂ d  (9.21)

3) Obliczamy ∂:

∂=Dt∂ (9.22)

4) Dokonujemy modyfikacji naprężeń:

u=0∂1 (9.23)

gdzie 0 jest naprężeniem przed aktualną iteracją.

σ

ε K (d) Δd Δp=

• odkształcenia przyrostowe 1) Obliczamy ∂ d :

∂ d =−kt−1⋅r (9.24)

2) Modyfikujemy przyrostowe przemieszczenia (od ostatniego stanu równowagi):

 dN= d0 d1 (9.25)

gdzie d0 jest przyrostem przemieszczenia od ostatniej iteracji.

3) Obliczamy przyrostowe odkształcenia:

= f  d  (9.26)

4) Wyznaczamy przyrostowe naprężenia:

=Dt (9.27)

5) Modyfikujemy naprężenia:

u=01 (9.28)

gdzie 0 jest naprężeniem na końcu ostatniego przyrostu.

λ_p