Podciąg i WKW zbieżności ciągu

(1)

Ciągi liczbowe

Autorzy:

Katarzyna Czyżewska

(2)

Spis treści

Definicja ciągu Ciąg monotoniczny Ciąg ograniczony Granica ciągu

Własności granic ciągów

Symbole oznaczone i nieoznaczone w granicy ciągu Twierdzenia pozwalające wyliczać granice ciągów Granice pewnych ciągów specjalnych

Metody obliczania granic ciągów Podciąg i WKW zbieżności ciągu

(3)

Definicja ciągu

Idea ciągu, w różnej formie, towarzyszy każdemu z nas w dniu codziennym. Kolejka do lekarza, układ haseł w encyklopedii, czy cyfry tworzące numer konta bankowego, to wszystko są przykłady ciągów. Widzimy jednak różnicę między ciągiem będącym np. alfabetyczną listą studentów w grupie, a ciągiem, który jest spisem dat w kalendarzu. Jeden z nich jest z konieczności ciągiem skończonym, tzn. posiadającym skończoną liczbę wyrazów, a drugi wydaje się ciągnąć w nieskończoność.

Z matematycznego punktu widzenia układ liczb lub innych obiektów (niekoniecznie matematycznych) tworzy ciąg, jeżeli każdemu elementowi przypiszemy jednoznacznie odpowiadające mu miejsce w ciągu, czyli liczbę naturalną. Najbardziej oczywistym przykładem ciągu liczbowego są liczby naturalne, ponieważ wartość liczby jednocześnie podaje numer miejsca, na którym ona stoi w ciągu.

PRZYKŁAD

Przykład 1: Idea tworzenia ciągu liczbowego

Widzimy, że na każdym miejscu, opisanym przez kolejną liczbę naturalną ustawiamy wyrazy ciągu, które w przykładzie są wielokrotnościami liczby . Procedura taka może oczywiście zatrzymać się w pewnym miejscu, ale może też ciągnąć się w nieskończoność.

DEFINICJA

Definicja 1: Ciąg liczbowy

Ciągiem liczbowym o wyrazach rzeczywistych nazywamy funkcję , która elementom podzbioru zbioru liczb naturalnych ( ) przyporządkowuje liczby rzeczywiste.

UWAGA

Uwaga 1: Oznaczenie ciągu

Wartość ciągu dla argumentu nazywamy -tym wyrazem ciągu i oznaczamy przez dla , natomiast cały ciąg oznaczamy przez , lub w skrócie . Jeżeli mówimy o kilku ciągach jednocześnie, to dla odróżnienia oznaczamy je różnymi literami np. itd.

miejsce w ci

ą

gu:

wyraz ci

ą

gu:

1,

3,

2,

6,

3,

9,

12,

4,

15,

5,

18,

6,

21,

7,

…

3 a : M → R

M

N M ⊂ N

a

n ∈ M

n

a

n

= a(n) ∈ R

n ∈ M

(a

n

)

n∈M

( )

a

n

( ), ( ), …, ( ), ( )

a

n

b

n

x

n

y

n

(4)

DEFINICJA

Definicja 2: Ciąg skończony

Jeżeli dziedzina ciągu jest zbiorem skończonym (np. ), to mówimy, że jest ciągiem skończonym ( -wyrazowym).

PRZYKŁAD

Przykład 2: Skończone ciągi liczbowe

a) jest skończonym -cio wyrazowym ciągiem arytmetycznym o pierwszym wyrazie i różnicy

b) jest ciągiem cyfr w zapisie dwójkowym liczby , czyli jest -wyrazowym ciągiem zero-jedynkowym

c) jest ciągiem kolejnych dwucyfrowych liczb pierwszych, czyli

jest -wyrazowym ciągiem liczb dwucyfrowych

DEFINICJA

Definicja 3: Ciąg nieskończony

Jeżeli dziedzina ciągu jest zbiorem nieskończonym (np. lub zbór liczb parzystych), to mówimy, że jest ciągiem nieskończonym.

PRZYKŁAD

Przykład 3: Nieskończone ciągi liczbowe

a) jest nieskończonym ciągiem geometrycznym o pierwszym wyrazie i ilorazie

b) jest nieskończonym ciągiem pól figur, które tworzymy następująco: w kwadrat o boku wpisujemy koło, w powstałe koło wpisujemy kwadrat, w który wpisujemy kolejne koło itd., czyli

c) jest ciągiem Fibonacciego tzn. dwa pierwsze wyrazy ciągu równe są , a każdy następny jest sumą dwóch wyrazów poprzednich, czyli

M

a

M = {1, 2, …, n}

a

n

( ) = (−8, −3, 2, 7, 12, 17)

a

n

6 −8

5 ( )

b

n

2014

( ) = (1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0)

b

n

11 ( )

c

n

( ) = (11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 91, 97)

c

n

22 M

a

M = N

M =

a

( ) = (1, , , , , …)

a

n 1₃ 1₉ ₂₇1 ₈₁1

1

1₃

( )

b

n

1 ( ) = (1, , , , , , …)

b

n π₄ 1₂ π₈ 1₄ ₁₆π

( )

c

n

1 ( ) = (1, 1, 2, 3, 5, 8, 13, 21, …)

c

n

(5)

UWAGA

Uwaga 2:

Jeżeli dziedzina ciągu nie jest określona jako podzbiór , to przyjmujemy, że jest to cały zbiór .

Komentarz Komentarz

Zgodnie z definicją ciągu możemy podawać ciąg jako funkcję, czyli podać wzór -tego wyrazu ciągu np. w przykładzie Idea tworzenia ciągu liczbowego wzór na -ty wyraz to , a w przykładzie Nieskończone ciągi liczbowe a) . Zaletą takiego określenia ciągu jest to, że możemy natychmiast wyliczyć dowolny wyraz ciągu podstawiając do wzoru odpowiednie

. Inną z możliwości jest opisanie metody jak należy szukać kolejnych wyrazów ciągu, np. w przykładzie Nieskończone ciągi liczbowe b) szukamy kolejnych figur geometrycznych zgodnie z opisem, a następnie wyliczamy ich pola. Możemy również podać procedurę jak tworzyć kolejne wyrazy ciągu za pomocą wyrazów poprzednich, tzw. procedurę rekurencyjną, należy pamiętać jednak o podaniu wartości odpowiedniej ilości wyrazów początkowych tak, aby procedura mogła wystartować, np. w przykładzie Nieskończone ciągi liczbowe c) procedurę można opisać następująco

Wadą tej metody określania ciągu jest to, że musimy znać wyrazy poprzednie ciągu, aby wyliczyć wyraz kolejny, co oczywiście jest w praktyce niewygodne, gdy chcemy obliczyć wyraz dla dużego . Kolejną często spotykana metodą zadania ciągu jest podanie kilku jego początkowych wyrazów, tak, aby można było zauważyć schemat tworzenia wyrazów następnych, np. przykład

Nieskończone ciągi liczbowe a), w którym widać, że każdy następny wyraz powstaje z poprzedniego przez przemnożenie go przez . Przy tej metodzie wadą jest to, że należy podać odpowiednio dużo wyrazów początkowych, żeby można było zauważyć schemat, a następnie sprawdzić, czy jest poprawny.

DEFINICJA

Definicja 4: Metody określania ciągu

Podstawowymi metodami określania ciągu są: 1. podanie wzoru na -ty wyraz ciągu, np. 2. podanie wzoru rekurencyjnego, np.

3. opisanie sposobu tworzenia kolejnych wyrazów, np. jest kolejnym wyrazem rozwinięcia dziesiętnego liczby 4. podanie kilku wyrazów początkowych ciągu, aby wiadomo było, według jakiej zasady należy tworzyć wyrazy następne,

np.:

Zgodnie z definicją ciągu, może on być przedstawiony graficznie w postaci wykresu, gdzie na osi odciętych zaznaczamy kolejne liczby naturalne i w układzie współrzędnych zaznaczamy punkty . Widzimy więc, że wykres ciągu składa się z izolowanych punktów w układzie współrzędnych.

M ⊂ N

N

n

a

n

= 3n

a

n

=

₃n−11

n ∈ N

.

⎧

⎩

⎨

⎪

= 1

a

1

= 1

a

2

=

+

, n ≥ 1

a

n+2

a

n

a

n+1

n

1 3

n

a

n

=

1− n+1

, =

2 √[3 (n+3) log3

a

n 6n−8 4+ arcsin(_√ n−2)

{

_{= 6– 2 +}

a1

= 3

,

a

n+1

a

n

√

− −

1 + a

−−−

n

⎧

⎩

⎨

⎪

= 1

a1

= 2

a2

=

a

n+2 an+₂an+1

a

n

√

5 ( ) = ( , , , , …).

a

n 1₂ 2₃ 3₄ 4₅

(n, )

a

n

(6)

a 1 2 3 4 5 6 7 8 9 10 n 1 2 3 4 5 6 7 8 9 10 n a a a a a a a a a a

Rysunek 1: Wykres ciągu składający się z izolowanych punktów w układzie współrzędnych

Wadą takiej graficznej interpretacji ciągu jest to, że zawsze możemy zobaczyć tylko kilka początkowych wyrazów ciągu, czyli w sytuacji, gdy interesować nas będzie zachowanie się ciągu dla bardzo dalekich wyrazów, taka interpretacja jest bezużyteczna. Wygodniej będzie przedstawiać ciąg tylko na osi rzędnych, czyli zrzutować prostopadle punkty reprezentujące wyrazy ciągu na tę oś. Zauważmy, że ten drugi sposób pozwala na umieszczenie na Rys. 1 większej ilości wyrazów ciągu.

DEFINICJA

Definicja 5: Interpretacja geometryczna ciągu

Graficznie ciąg możemy przedstawiać w postaci wykresu funkcji o argumentach naturalnych, otrzymując pełny wykres ciągu lub w postaci rzutu tego wykresu na oś wartości, otrzymując uproszczony wykres ciągu.

Ciąg monotoniczny

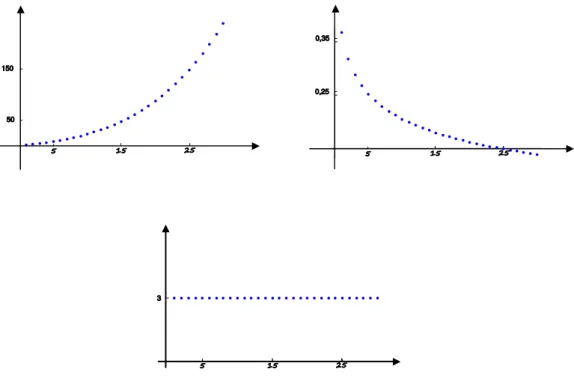
Ciągi, tak jak funkcje, mogą mieć różne własności, których znajomość może przyczynić się do dalszej analizy ich zachowania. Na wykresach ciągów z Rys. 2 widzimy, że charakter każdego z ciągów jest zupełnie inny.

0,35

0,25

3 50

150

Rysunek 2: Wykresy trzech ciągów o różnej monotoniczności

W pierwszym ciągu pokazanym na Rys. 2 każdy kolejny wyraz jest większy od wyrazów poprzednich i ciąg o takiej własności nazywamy rosnącym. W ciągu drugim każdy kolejny wyraz jest od poprzednich mniejszy i ciąg mający taką własność nazywamy

(7)

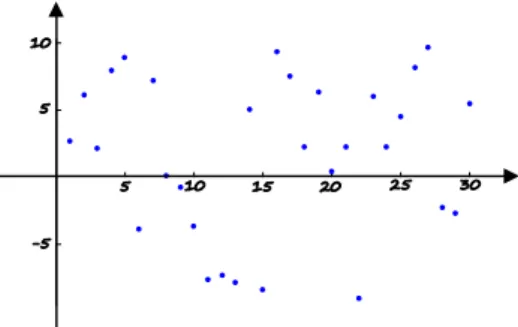
malejącym. W trzecim ciągu wszystkie wyrazy są takie same i taki ciąg nazywamy stałym. Może się również zdarzyć, że każdy kolejny wyraz ciągu jest nie mniejszy albo nie większy (tzn. może być też równy) od wyrazu poprzedniego i ciągi o takich własnościach nazywamy niemalejącym albo nierosnącym. Zauważmy, że ciąg stały jest jednocześnie niemalejący i nierosnący. Istnieją oczywiście ciągi, które nie są ani rosnące lub niemalejące, ani malejące lub nierosnące, ani stałe i mówimy, że taki ciąg nie jest monotoniczny. Rys. 3 przedstawia ciąg, który nie ma żadnej z powyższych własności.

Rysunek 3: Wykres ciągu, który nie jest ciągiem monotonicznym

Rzeczywiście, np. wyraz drugi jest większy od wyrazu pierwszego, wyraz trzeci jest natomiast mniejszy od drugiego, wyraz czwarty jest znowu większy od trzeciego itp.

DEFINICJA

Definicja 6: Ciąg rosnący

Mówimy, że ciąg jest rosnący, jeżeli dla wszystkich spełniona jest nierówność .

DEFINICJA

Definicja 7: Ciąg malejący

Mówimy, że ciąg jest malejący, jeżeli dla wszystkich spełniona jest nierówność .

DEFINICJA

Definicja 8: Ciąg stały

Mówimy, że ciąg jest stały, jeżeli dla wszystkich spełniona jest równość .

DEFINICJA

Definicja 9: Ciąg niemalejący

Mówimy, że ciąg jest niemalejący, jeżeli dla wszystkich spełniona jest nierówność .

(a

n

)

n∈M

n ∈ M

a

n+1

>

a

n

(a

n

)

n∈M

n ∈ M

a

n+1

<

a

n

(a

n

)

n∈M

n ∈ M

a

n+1

=

a

n

(8)

DEFINICJA

Definicja 10: Ciąg nierosnący

Mówimy, że ciąg jest nierosnący, jeżeli dla wszystkich spełniona jest nierówność .

UWAGA

Uwaga 3:

Jeżeli ciąg posiada jedną z wyżej wymienionych własności w całej swojej dziedzinie, to nazywamy go ciągiem monotonicznym.

Komentarz Komentarz

Definicję Ciąg rosnący można w sposób równoważny wyrazić w postaci nierówności , która powinna być spełniona dla każdego . Jeżeli dodatkowo wiemy, że wszystkie wyrazy ciągu są dodatnie, to ciąg jest rosnący, gdy dla wszystkich spełniona jest nierówność . Jeżeli w nierównościach zmienimy zwroty nierówności na przeciwne, to analogiczne warunki równoważne definiują ciąg malejący. Wypisane warunki są łatwiejsze do sprawdzenia w praktyce, gdyż wystarczy zbadać znak różnicy lub dla ciągów o wyrazach dodatnich przyrównać iloraz do jedynki, aby odpowiedzieć na pytanie o monotoniczność ciągu.

PRZYKŁAD

Przykład 4:

Zbadaj monotoniczność ciągu Rozwiązanie

Rozwiązanie

Zbadamy znak różnicy .

dla Widzimy, że różnica jest dodatnia dla wszystkich .

Wykazaliśmy, że ciąg jest rosnący.

(a

n

)

n∈M

n ∈ M

a

n+1

≤

a

n

−

> 0

a

n+1

a

n

n ∈ M

(a

n

)

n∈M

n ∈ M

an+1

> 1

an

−

a

n+1

a

n a_an+1_n

=

, n ∈ N

a

n 3n−1_n+3

−

a

n+1

a

n

−

=

−

=

> 0

a

n+1

a

n 3n+2n+4 3n−1n+3 (3n+2)(n+3)−(3n−1)(n+4)(n+4)(n+3) (n+4)(n+3)10

n ∈ N

−

a

n+1

a

n

n ∈ N

(a

n

)

n∈N

(9)

PRZYKŁAD

Przykład 5:

Zbadaj monotoniczność ciągu Rozwiązanie

Rozwiązanie

Zauważamy, że wszystkie wyrazy ciągu są dodatnie, więc obliczamy iloraz .

Iloraz jest mniejszy od jedynki dla wszystkich . Wykazaliśmy, że ciąg jest malejący.

PRZYKŁAD

Przykład 6:

Zbadaj monotoniczność ciągu . Rozwiązanie

Rozwiązanie

Określimy znak różnicy dla wszystkich .

dla

Obliczamy jeszcze i i zauważamy, że .

Wykazaliśmy, że różnica jest dodatnia dla wszystkich , czyli ciąg jest rosnący.

Komentarz Komentarz

Bardzo często analiza zachowania się ciągu liczbowego sprowadza się do badania zachowania się tego ciągu dla wyrazów o dużych indeksach, czyli nie interesuje nas zachowanie się początkowych wyrazów ciągu (nawet dużej ich ilości), a raczej „końcówka” tego ciągu. Z takiego punktu widzenia, może się zdarzyć, że dopiero po odrzuceniu pewnej liczby wyrazów początkowych, otrzymujemy ciąg monotoniczny i takie ciągi nazywamy monotonicznymi od pewnego miejsca.

= , n ∈ N

b

n ₂1n bn+1 bn

=

∶

=

⋅

= < 1.

bn+1 bn 1 2n+1 ₂1n ₂n+11

2

n 1₂ bn+1 bn

n ∈ N

(b

n

)

n∈N

=

, n ≥ 2

c

n

√

n

−

−−−−

2

− 2n

−

c

n+1

c

n

n ≥ 2

− =

−

= (

−

) ⋅

=

c

n+1

c

n

√

(n + 1 − 2(n + 1)

−

−−−−−−−−−−−−−

)

2

−

√

−

n

−−−−

2

− 2n

−

√

− −

n

−−−

2

− 1

√

n

−

−−−−

2

− 2n

−

n−1+ 2 √ _√n2−2n + −1 n2 √ _√n2−2n n−1− +2n 2 _n2 + −1 n2 √ _√n2−2n

=

2n−1

> 0

+ −1 n2 √ _√n2−2n

n ≥ 3.

=

c

3

√

3 c

2

= 0

c

3

− > 0

c

2

−

c

n+1

c

n

n ≥ 2

(c

n

)

n≥2

(10)

0,3 0,1 -0,1 5 15 25 2 1 -1 5 15 25 25 15 5 0,5 1,5

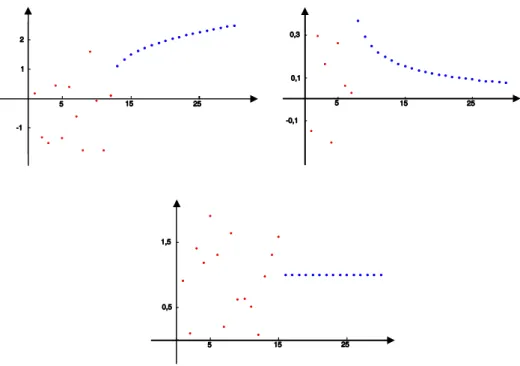
Rysunek 4: Wykresy trzech ciągów, których monotoniczność ustala się dopiero od pewnego wyrazu

Rys. 4 przedstawia wykresy trzech ciągów, których monotoniczność ustala się dopiero od pewnego wyrazu, a nie od wyrazu pierwszego, jak to ma miejsce dla ciągów monotonicznych. Rzeczywiście pierwszy wykres przedstawia ciąg, który jest rosnący począwszy od 11-go wyrazu. Drugi wykres przedstawia ciąg, który jest malejący począwszy od 8-go wyrazu, a wykres trzeci przedstawia ciąg, który jest stały od 16-go wyrazu.

DEFINICJA

Definicja 11: Ciąg rosnący od pewnego miejsca

Jeżeli dziedziną ciągu jest i istnieje takie, że dla każdego spełniona jest nierówność , to mówimy, że ciąg jest rosnący od pewnego miejsca.

DEFINICJA

Definicja 12: Ciąg malejący od pewnego miejsca

Jeżeli dziedziną ciągu jest i istnieje takie, że dla każdego spełniona jest nierówność , to mówimy, że ciąg jest malejący od pewnego miejsca.

DEFINICJA

Definicja 13: Ciąg stały od pewnego miejsca

Jeżeli dziedziną ciągu jest i istnieje takie, że dla każdego spełniona jest równość , to mówimy, że ciąg jest stały od pewnego miejsca.

( )

a

n

N

n

0

∈ N

n ≥ n

0

a

n+1

>

a

n

( )

a

n

N

n0

∈ N

n ≥ n0

a

n+1

<

a

n

(11)

PRZYKŁAD

Przykład 7:

Rozwiązanie

Dziedziną ciągu jest zbiór . Badamy znak różnicy .

dla .

Widzimy, że różnica jest dodatnia tylko dla , czyli ciąg jest rosnący od 3-go miejsca.

PRZYKŁAD

Przykład 8:

Rozwiązanie

Dziedziną ciągu jest zbiór . Badamy znak różnicy .

dla .

Widzimy, że różnica jest ujemna tylko dla , czyli ciąg jest malejący od 5-go miejsca.

Ciąg ograniczony

Zbadajmy zachowanie się ciągów ze względu na własność ograniczoności.

5 10 15 20 25 30 0.5 1.0 1.5 2.0 5 5 5 5 0 0 0 0 0

Rysunek 5: Ciąg ograniczony od góry

Rys. 5 przedstawia wykres ciągu, którego wszystkie wyrazy są mniejsze od liczby A=2.

=

− 6n + 8

a

n

2

N

a

n+1

−

a

n

−

= (n + 1 − 6(n + 1) + 8 − ( − 6n + 8) = 2n − 5 > 0

a

n+1

a

n

)

2

n

2

n >

5₂

−

a

n+1

a

n

n >

5₂

(a

n

)

n∈N

=

b

n _1+(n−5)1 2

N

b

n+1

−

b

n

− =

−

=

< 0

b

n+1

b

n _1+(n−4)1 2 _1+(n−5)1 2 _{[1+(n−4 ][1+(n−5 ]}−2n+9₎2 ₎2

n >

9₂

−

b

n+1

b

n

n >

9₂

(b

n

)

n∈N

(12)

5 10 15 20 25 30 2.0 2.5 0 5 0 5 0 5 0

Rysunek 6: Ciąg ograniczony od dołu

Rys. 6 przedstawia wykres ciągu, którego wszystkie wyrazy są większe od liczby A=-1,6.

Na Rys. 5 i Rys. 6 widzimy wykresy dwóch ciągów, przy czym wszystkie wyrazy pierwszego ciągu są mniejsze od pewnej liczby rzeczywistej i taki ciąg nazywamy ciągiem ograniczonym od góry, podczas gdy wszystkie wyrazy drugiego ciągu są większe od pewnej liczby rzeczywistej i nazywamy go ciągiem ograniczonym od dołu.

3

1

-1

-3

5 15 25

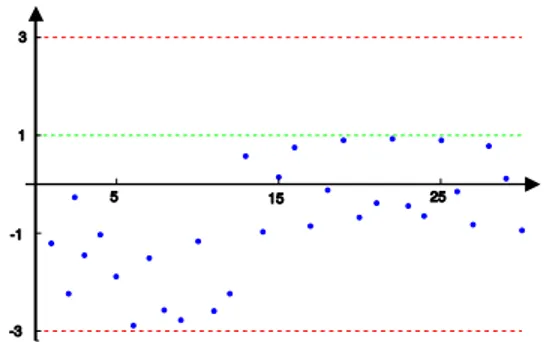
Rysunek 7: Wykres ciągu, którego wszystkie wyrazy są mniejsze od liczby 1, ale większe od liczby -3

Rys. 7 przedstawia wykres ciągu, którego wszystkie wyrazy są mniejsze od liczby 1, ale większe od liczby -3. Oznacza to, że wszystkie wyrazy tego ciągu leżą w przedziale .

Istnieją również ciągi, które są ograniczone zarówno od góry, jak i od dołu i taki ciąg nazywamy ograniczonym. Zauważamy, że wszystkie wyrazy ciągu ograniczonego leżą w przedziale , dla pewnej liczby .

5 10 15 20 25 30 - 60 - 40 - 20 20 40 0 0 0 0 0 0 5 0 5 0

Rysunek 8: Ciąg nieograniczony

Rys. 8 przedstawia wykres ciągu, dla którego znajdą się wyrazy zarówno większe jak i mniejsze od dowolnej liczby rzeczywistej. Ciąg taki nie spełnia więc żadnego z warunków ograniczoności.

W przypadku, gdy nie znajdziemy takiej liczby, od której wszystkie wyrazy ciągu byłyby mniejsze, lub takiej, od której wszystkie wyrazy byłyby większe, to ciąg o tej własności nazywamy nieograniczonym.

[−3, 3]

(13)

DEFINICJA

Definicja 14: Ciąg ograniczony od góry

Mówimy, że ciąg jest ograniczony od góry, jeżeli istnieje liczba taka, że dla każdego zachodzi .

DEFINICJA

Definicja 15: Ciąg ograniczony od dołu

Mówimy, że ciąg jest ograniczony od dołu, jeżeli istnieje liczba taka, że dla każdego zachodzi .

DEFINICJA

Definicja 16: Ciąg ograniczony

Mówimy, że ciąg jest ograniczony, jeżeli ciąg jest ograniczony od dołu i od góry, co jest równoważne warunkowi, że istnieje liczba taka, że dla każdego zachodzi .

Aby analitycznie zbadać, czy ciąg jest ograniczony od góry (albo od dołu) należy znaleźć liczbę rzeczywistą, dla której

spodziewamy się, że każdy wyraz ciągu będzie od niej mniejszy (albo większy), a następnie udowodnić, że rzeczywiście tak jest. Znaleźć taką liczbę można korzystając z wykresu ciągu lub z ogólnych zasad pozwalających ograniczać wartości wyrażeń. Warto zauważyć prosty fakt, że ciąg rosnący jest zawsze ograniczony od dołu, a ciąg malejący jest ograniczony od góry przez swój pierwszy wyraz.

PRZYKŁAD

Przykład 9:

Zbadaj ograniczoność ciągu . Rozwiązanie

Rozwiązanie

Zauważamy, że ciąg jest malejący, bo

Zatem dla każdego , .

Z drugiej strony dla wszystkich , czyli ciąg jest ograniczony.

( )

a

n

A ∈ R

n ∈ N

a

n

≤ A

( )

a

n

A ∈ R

n ∈ N

a

n

≥ A

( )

a

n

( )

a

n

A > 0

n ∈ N

| | ≤ A

a

n

=

a

n _3+n1

a

n

−

=

−

=

< 0

a

n+1

a

n _4+n1 _3+n1 _(4+n)(3+n)−1

n ∈ N

a

n

<

a

1

=

1₄

> 0

a

n

( )

a

n

(14)

PRZYKŁAD

Przykład 10:

Zbadaj ograniczoność ciągu . Rozwiązanie

Rozwiązanie

Zauważamy, że ciąg inaczej zachowuje się dla parzystych, a inaczej dla nieparzystych. Dla parzystych .

Pokażemy, że dla dowolnego od pewnego miejsca .

Rzeczywiście, nierówność jest spełniona dla każdego , a dla mamy

czyli zawsze znajdziemy tak duże , dla którego , a zatem ciąg nie jest ograniczony od góry. Analogicznie pokazujemy, że dla n nieparzystych, dla dowolnego , od pewnego miejsca .

Wykazaliśmy, że ciąg nie jest ograniczony od góry, ani od dołu.

Granica ciągu

Dla kolejnych rozważań zakładamy, że ciąg jest nieskończony. Zastanówmy się, jak zachowują się wyrazy ciągu , jeżeli jest coraz większe, czyli mówimy, że zmierza do nieskończoności. Na Rys. 9 widzimy ciąg o wyrazach dodatnich, którego wyrazy, wraz ze wzrostem wartości , coraz bardziej zbliżają się do liczby zero, nigdy tej wartości nie osiągając. Jeżeli jednak wybierzemy liczbę , dowolnie bliską zeru, to nieskończenie wiele wyrazów ciągu leży w przedziale .

Rysunek 9: Granica właściwa ciągu

DEFINICJA

Definicja 17: Granica właściwa ciągu

Mówimy, że ciąg nieskończony ma granicę właściwą , jeżeli dla dowolnej liczby od pewnego miejsca zachodzi

warunek .

Komentarz Komentarz

W wielu sytuacjach warto wiedzieć czy wyrazy rozważanego ciągu mają tendencję do skupiania się wokół jakiejś liczby. Gdyby

=

b

n (−4) n 1+2n

n

b

n

=

₁₊₂4nn

A

b

n

> A

A < 0

A ≥ 0

> A ⇔

− A − A > 0

− At − A > 0 ⇒

>

⇔ n >

4n 1+2n

4

n

2

n

⟺

t=2n

t

2

₂

n A+_√A2+4A 2

log

2A+ A+4A 2 √ 2

n ∈ N

b

n

> A

( )

b

n

A

b

n

< A

( )

b

n

( )

a

n

( )

a

n

ε > 0

[−ε, ε]

( )

a

n

g

ε > 0

| − g| < ε

a

n

(15)

rzeczywiście tak było, to znajomość tej liczby pozwala „zlokalizować” nasz ciąg na osi. Oznacza to, że prawie wszystkie, poza skończoną ilością, wyrazy naszego ciągu leżą w pobliżu danej liczby, którą nazywamy granicą ciągu. Fakt, że liczba jest granicą właściwą ciągu oznacza więc, że prawie wszystkie (tzn. wszystkie od pewnego miejsca) wyrazy ciągu leżą w przedziale

, a ponieważ może być dowolnie małe, tak więc dowolnie blisko liczby znajduje się nieskończenie wiele wyrazów ciągu

UWAGA

Uwaga 4: Oznaczenie

Fakt, że liczba jest granicą właściwą ciągu oznaczamy symbolicznie i mówimy, że ciąg jest zbieżny do liczby przy zmierzającym do nieskończoności.

UWAGA

Uwaga 5:

Pojęcie granicy ciągu możemy zdefiniować formalnie

PRZYKŁAD

Przykład 11:

Pokaż, że , ,

Rozwiązanie:

Aby wykazać, że liczba jest granicą ciągu weźmiemy dowolną liczbę i wykażemy, że uda się znaleźć taką liczbę naturalną , że dla wszystkich zachodzi nierówność .

Zauważamy, że zachodzą ograniczenia dla

czyli, gdyby liczba była liczbą naturalną, to można byłoby przyjąć , ale ponieważ, z reguły, nie jest to liczba naturalna, to przyjmujemy , gdzie oznacza część całkowitą z liczby rzeczywistej . Dla tak dobranego i dowolnej liczby zachodzi wtedy nierówność , czyli , a to właśnie mieliśmy wykazać.

g

( )

a

n

(g − ε, g + ε)

ε

g

( )

a

n

g

( )

a

n

lim

n→∞

a

n

= g

( )

a

n

g

n

= g wtedy i tylko wtedy, gdy ∀ε > 0 ∃ ∈ N ∀n ⩾

| − g| < ε

lim

n→∞

a

n

n0

a

n

= 0

lim

n→∞ _n1

lim

n→∞

(− ) = 0

_n1

lim

n→∞ (−1)

= 0

n n

0 ( )

a

n

ε > 0

n0

n ⩾ n0

| − 0| < ε

a

n

| − 0| = | − − 0| = |

1

− 0| = < ε

n 1n (−1) n n n1

n >

1ε 1 ε

n

0

=

1ε

= [ ] + 1

n0

1 ε

[x]

x

n0

n ⩾ n

0 1n

< ε

| − 0| < ε

a

n

(16)

PRZYKŁAD

Przykład 12:

Wykaż, że dla dowolnego . Rozwiązanie:

Dla dowolnie wybranego mamy znaleźć spełniające warunek dla i . Zauważamy, że

Jeżeli weźmiemy , to , a co za tym idzie dla .

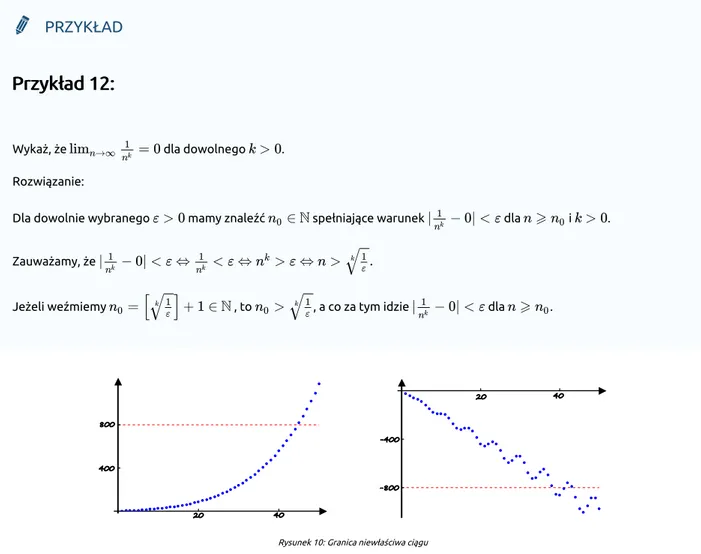
Rysunek 10: Granica niewłaściwa ciągu

Zauważamy, że ciągi z Rys. 10 zachowują się, przy zmierzającym do nieskończoności, inaczej niż ciąg zbieżny do pewnej granicy . Jeżeli wybierzemy dowolnie dużą liczbę , to nieskończenie wiele wyrazów ciągu pierwszego jest większych od liczby , oraz nieskończenie wiele wyrazów ciągu drugiego jest mniejszych od liczby . Z dowolności wyboru liczby wnioskujemy, że wyrazy żadnego z obydwu ciągów nie lokalizują się w pobliżu żadnej liczby rzeczywistej. Mówimy wtedy, że ciąg jest rozbieżny do

, w pierwszym przypadku, albo do , w drugim przypadku.

DEFINICJA

Definicja 18: Granica niewłaściwa

ciągu

Mówimy, że ciąg ma granicę niewłaściwą , jeżeli dla dowolnej liczby od pewnego miejsca zachodzi nierówność .

DEFINICJA

Definicja 19: Granica niewłaściwa

ciągu

Mówimy, że ciąg ma granicę niewłaściwą , jeżeli dla dowolnej liczby od pewnego miejsca zachodzi nierównośc .

= 0

lim

n→∞ _n1k

k > 0

ε > 0

n

0

∈ N

| − 0| < ε

_n1k

n ⩾ n

0

k > 0

| − 0| < ε ⇔

1

< ε ⇔

> ε ⇔ n >

.

nk _n1k

n

k

√

k 1_ε

= [

] + 1 ∈ N

n0

1 ε

√

k

_n0

>

1 ε

√

k

| − 0| < ε

1 nk

n ⩾ n0

n

g

E > 0

E

−E

E

+∞

−∞

+∞

( )

a

n

+∞

E > 0

> E

a

n

−∞

( )

a

n

−∞

E > 0

< −E

a

n

(17)

UWAGA

Uwaga 6:

Fakt, że ciąg ma granicę niewłaściwą oznaczamy i mówimy, że ciąg jest rozbieżny do .

Definicję granicy niewłaściwej możemy zapisać symbolicznie

a granicy niewłaściwej

PRZYKŁAD

Przykład 13:

Pokaż, że Rozwiązanie:

Aby wykazać, że jest granicą niewłaściwą ciągu weźmiemy dowolną liczbę i wykażemy, że uda się znaleźć taką liczbę naturalną , że dla wszystkich zachodzi nierówność .

Nierówność sugeruje, że należy przyjąć , które jest liczbą naturalną większą od , czyli dla .

Aby wykazać, że jest granicą niewłaściwą ciągu weźmiemy dowolną liczbę i wykażemy, że uda się znaleźć taką liczbę naturalną , że dla wszystkich zachodzi nierówność .

Nierówność jest równoważna nierówności , czyli wykorzystujemy dobrane dla poprzedniego ciągu.

PRZYKŁAD

Przykład 14:

Wykaż, że dla .

Rozwiązanie:

Dla dowolnie wybranego mamy znaleźć , takie, że nierówność jest spełniona dla wszystkich i .

Zauważamy, że dla zachodzi , czyli dla i wszystkich zachodzi żądana nierówność .

( )

a

n

+∞

lim

n→∞

a

n

= +∞

( )

a

n

+∞

( )

a

n

−∞

lim

n→∞

a

n

= −∞

( )

a

n

−∞

+∞

= +∞ wtedy i tylko wtedy, gdy ∀E > 0 ∃ ∈ N ∀n ⩾ ( > E)

lim

n→∞

a

n

0

n

0

a

n

−∞

= −∞ wtedy i tylko wtedy, gdy ∀E > 0 ∃ ∈ N ∀n ⩾ ( < −E)

lim

n→∞

a

n

n0

a

n

n = +∞,

(−n) = −∞.

lim

n→∞

lim

n→∞

+∞

( )

a

n

E > 0

n

0

n ⩾ n

0

a

n

> E

n > E

n

0

= [E] + 1

E

n > E

n ⩾ n

0

−∞

( )

a

n

E > 0

n

0

n ⩾ n

0

a

n

< −E

−n < −E

n > E

n

0

= [E] + 1

= +∞

lim

n→∞

n

k

k > 0

E > 0

n

0

∈ N

n

k

> E

n ⩾ n

0

k > 0

n

k

> E ⇔ n >

_E

1_k

_n

₀

_{= [}

_E

1_k

_{] + 1}

_{n ⩾ n}

₀

> E

n

k

(18)

500

-500

10 20 30 40

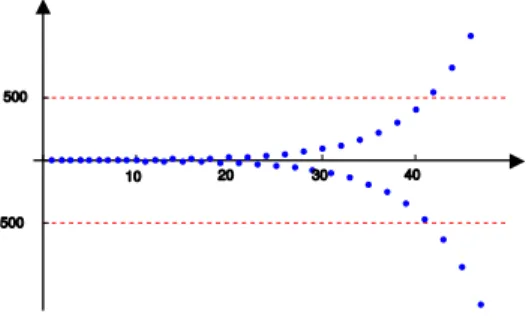
Rysunek 11: Ciąg rozbieżny

Na Rys. 11 widzimy wykres ciągu, który ma nieskończenie wiele wyrazów, większych od dowolnie wybranej liczby , ale równocześnie ma też nieskończenie wiele wyrazów, które są mniejsze od liczby . Wyrazy tego ciągu nie tylko nie lokalizują się wokół żadnej liczby rzeczywistej, ale również nie spełniają definicji ciągu rozbieżnego do , ani do . Taki ciąg nazywamy ciągiem rozbieżnym, albo ciągiem, który nie ma granicy.

DEFINICJA

Definicja 20: Ciąg rozbieżny

Ciąg, który nie posiada granicy właściwej ani niewłaściwej nazywamy ciągiem rozbieżnym.

PRZYKŁAD

Przykład 15:

Wykaż, że ciąg jest rozbieżny. Rozwiązanie:

Zauważamy, że ciąg przyjmuje na zmianę wartości albo .

Nie może to być ciąg rozbieżny do , bo dla żaden wyraz ciągu nie jest większy od E i analogicznie nie może być rozbieżny do , bo żaden wyraz ciągu nie jest mniejszy od .

Żadna liczba rzeczywista g różna od i nie może też być granicą właściwą ciągu , bo jeżeli wybierzemy przedział , który nie zawiera liczb i , to nie zawiera też żadnego wyrazu naszego ciągu. Liczba też nie może być granicą właściwą ciągu , ponieważ poza przedziałem , który nie zawiera liczby leży nieskończenie wiele wyrazów naszego ciągu. Analogicznie liczba nie może być granicą właściwą ciągu .

Zatem ciąg nie ma zarówno granicy właściwej, jak i niewłaściwej, czyli jest rozbieżny.

Własności granic ciągów

E > 0

– E

+∞

−∞

= (−1

a

n

)

n

( )

a

n

1 −1

+∞

E = 2

−∞

−E

1 −1

( )

a

n

(g − ε, g + ε)

1 −1

1 ( )

a

n

(1 − ε, 1 + ε)

−1

( )

a

n

( )

a

n

(19)

Rysunek 12: Interpretacja geometryczna własności ograniczoności ciągu zbieżnego

Rys. 12 przedstawia wykres ciągu, który jest zbieżny do granicy . Ponieważ wiemy z definicji granicy ciągu, że prawie wszystkie jego wyrazy leżą w przedziale i poza tym przedziałem leży tylko skończona liczba wyrazów ciągu, więc jeżeli są wyrazy większe od , to żaden wyraz ciągu nie będzie większy niż największy z tych, które są większe od .

Analogicznie rozumujemy ograniczając ciąg od dołu albo przez liczbę , albo przez najmniejszy z wyrazów, które są mniejsze od .

WNIOSEK

Wniosek 1:

Jeżeli , to ciąg jest ograniczony.

Rysunek 13: Przykład ciągu ograniczonego, który nie jest zbieżny

Rys. 13 przedstawia wykres ciągu, który jest ograniczony, ale nie posiada granicy właściwej. Przykład ten pokazuje, że własność ograniczoności ciągu nie jest tożsama ze zbieżnością, czyli istnieją ciągi, które są ograniczone i nie mają granicy właściwej.

UWAGA

Uwaga 7:

Nie zachodzi twierdzenie odwrotne do wniosku, czyli nie każdy ciąg ograniczony musi być zbieżny do granicy właściwej.

2 [1, 3]

3

1

1 = g

lim

n→∞

a

n

( )

a

n

(20)

Rysunek 14: Interpretacja geometryczna braku ograniczoności ciągów rozbieżnych do i

Rys. 14 przedstawia dwa ciągi, z których pierwszy jest rozbieżny do , a drugi rozbieżny do . Zauważamy, że prawie wszystkie wyrazy pierwszego ciągu są większe od dowolnej liczby rzeczywistej oraz prawie wszystkie wyrazy drugiego ciągu są mniejsze od dowolnej liczby rzeczywistej.

WNIOSEK

Wniosek 2:

Jeżeli , to ciąg nie jest ograniczony od góry. Jeżeli , to ciąg nie jest ograniczony od dołu.

UWAGA

Uwaga 8:

Tak samo jak w przypadku Twierdzenia 1 nie zachodzą twierdzenia odwrotne, czyli ciąg, który nie jest ograniczony od góry nie musi być rozbieżny do , ani ciąg, który nie jest ograniczony od dołu nie musi być rozbieżny do .

Rysunek 15: Ciąg, który nie ma granicy

Rys. 15 pokazuje ciąg, którego nieskończenie wiele wyrazów leży dowolnie blisko liczby , ale również nieskończenie wiele wyrazów leży dowolnie blisko liczby .

Jeżeli wybierzemy , to poza przedziałami oraz leży zawsze nieskończenie wiele wyrazów ciągu, czyli liczby ani nie mogą być granicami ciągu. Tym bardziej granicą nie może być żadna inna liczba rzeczywista różna od i . Pokazuje to, że nawet jeżeli nieskończenie wiele wyrazów ciągu skupia się wokół pewnej liczby rzeczywistej, to nie musi ona być granicą ciągu.

+∞ −∞

+∞

−∞

= +∞

lim

n→∞

a

n

( )

a

n

= −∞

lim

n→∞

a

n

( )

a

n

+∞

−∞

1 −1

ε ∈ (0, 1)

[1 − ε, 1 + ε]

[−1 − ε, −1 + ε]

1 −1

(21)

TWIERDZENIE

Twierdzenie 1: o jednoznaczności granicy ciągu

Ciąg nie może mieć różnych granic.

Rysunek 16: Interpretacja geometryczna twierdzenia o zachowaniu nierówności w granicy

Rys. 16 przedstawia na jednym wykresie dwa ciągi zbieżne, z których jeden (czerwony) ma wyrazy od pewnego miejsca większe niż drugi (niebieski). Wydaje się być oczywiste, że granica ciągu o wyrazach większych nie może być mniejsza od granicy ciągu o wyrazach mniejszych. Już nie taki oczywisty jest fakt, że granice te mogą być równe, mimo, że pomiędzy wyrazami zachodzą nierówności silne.

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: o zachowaniu nierówności w granicy

o zachowaniu nierówności w granicy

Jeżeli i oraz od pewnego miejsca zachodzą nierówności pomiędzy odpowiednimi wyrazami ciągów , to pomiędzy granicami ciągów zachodzi nierówność .

UWAGA

Uwaga 9:

W granicy zachowana jest nierówność o tym zwrocie jak pomiędzy wyrazami dwóch ciągów, ale zawsze jako nierówność słaba.

Rysunek 17: Interpretacja geometryczna twierdzenia o ciągu ograniczonym i monotonicznym

Rys. 17 przedstawia dwa ciągi ograniczone, z których jeden jest rosnący (niebieski), a drugi malejący (czerwony). Zauważamy, że obydwa ciągi mają granice właściwe, ciąg rosnący i ograniczony od góry jest zbieżny do najmniejszego swojego ograniczenia górnego, a ciąg malejący i ograniczony od dołu jest zbieżny do największego swojego ograniczenia dolnego.

( )

a

n

2 = a

lim

n→∞

a

n

lim

n→∞

b

n

= b

<

(22)

TWIERDZENIE

Twierdzenie 3:

Twierdzenie 3: o ciągu ograniczonym i monotonicznym

o ciągu ograniczonym i monotonicznym

Jeżeli ciąg jest ograniczony i monotoniczny, to jest zbieżny.

PRZYKŁAD

Przykład 16:

Uzasadnij zbieżność ciągu Rozwiązanie:

Zbadamy monotoniczność ciągu wyznaczając znak różnicy dla wszystkich n naturalnych. Ponieważ różnica jest dodatnia, to ciąg jest rosnący.

Wystarczy teraz zbadać, czy ciąg jest ograniczony od góry, bo wiemy, że ciąg rosnący jest ograniczony od dołu przez

pierwszy wyraz. Wykorzystujemy ograniczenie .

Zauważamy, że jest sumą ciągu geometrycznego o pierwszym wyrazie i ilorazie . Ze wzoru na -tą

sumę ciągu geometrycznego mamy .

Z powyższego oszacowania wnioskujemy, że ciąg jest ograniczony, zatem twierdzenie mówi , że jest zbieżny.

PRZYKŁAD

Przykład 17:

Uzasadnij zbieżność ciągu Rozwiązanie:

Badamy monotoniczność ciągu zauważając, że jest to ciąg o wyrazach dodatnich, czyli możemy badać iloraz .

Ponieważ iloraz jest dla wszystkich naturalnych mniejszy od jedynki, to ciąg jest malejący.

Badamy teraz, czy ciąg jest ograniczony od dołu, gdyż wiemy, że ciąg malejący jest ograniczony od góry przez pierwszy wyraz.

Zauważamy, że dla wszystkich naturalnych, zatem ciąg jest ograniczony. Na podstawie twierdzenia wnioskujemy, że ciąg jest zbieżny.

( )

a

n

=

+

+ ⋯ +

.

a

n _1⋅211 _2⋅212 _n⋅21n

−

=

> 0

a

n+1

a

n _(n+1)⋅21 n+1

−

a

n+1

a

n

( )

a

n

=

+

+ ⋯ +

< + + ⋯ +

a

n _1⋅211 _2⋅212 _n⋅21n ₂11 ₂12 ₂1n

+ + ⋯ +

1 21 ₂12 ₂1n 1₂ 1₂

n

+ + ⋯ +

=

= 1 − (

< 1

1 21 ₂12 ₂1n 1₂ 1−(1 2)n 1−1 2 1 2

)

n

( )

a

n

=

.

b

n (n!) 2 (2n)!

( )

b

n

=

< 1

bn+1 bn [(n+1)!]2 (2n+2)! (2n)!(n!)2 [(n+1)⋅n!]2 (2n+2)⋅(2n+1)⋅(2n)! (2n)!(n!)2 _2(2n+1)n+1 bn+1 bn

n

( )

b

n

( )

b

n

=

> 0

b

n (n!) 2 (2n)!

n

( )

b

n

( )

b

n

(23)

Symbole oznaczone i nieoznaczone w granicy ciągu

Na wyrazach dwóch lub więcej ciągów możemy wykonywać działania arytmetyczne otrzymując nowy ciąg. Jeżeli ciągi wyjściowe były zbieżne, to analogiczne działania arytmetyczne można również wykonywać na granicach właściwych tych ciągów, ale także na granicach niewłaściwych otrzymując symbole graniczne ujmowane w nawisy kwadratowe, dla zaznaczenia, że nie są to działania wykonywane na liczbach, tylko na granicach. Niektóre z tych symboli dają zawsze ten sam wynik, bez względu na to jakie ciągi składowe dają określony symbol graniczny i nazywamy je symbolami oznaczonymi. Niektóre znów dają różne wyniki w zależności od tego, na jakich ciągach wykonujemy działania i takie symbole nazywamy nieoznaczonymi.

DEFINICJA

Definicja 21: Symbol oznaczony i nieoznaczony

Symbolem oznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i które daje zawsze taki sam wynik zależny tylko od granic ciągów, z których powstaje symbol graniczny. Symbolem nieoznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i którego wartości nie da się jednoznacznie obliczyć na podstawie jedynie granic ciągów, z których powstaje symbol graniczny.

UWAGA

Uwaga 10:

Do obliczania symboli oznaczonych służą odpowiednie twierdzenia podające wartości konkretnych symboli granicznych. Nie istnieją natomiast ogólne twierdzenia pozwalające obliczyć wartość symbolu nieoznaczonego i w każdym przypadku indywidualnie należy, stosując odpowiednie przekształcenie algebraiczne, zamienić symbol nieoznaczony na oznaczony.

2,0 10 20 30 1,0 0,5 1,5 2,5 3,0 40 50 60 70 80

Rysunek 18: Interpretacja geometryczna symbolów oznaczonych i

Rys. 18 przedstawia dwa ciągi, z których jeden (czerwony) powstaje z drugiego (niebieskiego) poprzez operację odwrócenia wyrazów ciągu tzn. . Zauważamy, że jeżeli ciąg wyjściowy jest rozbieżny do , to ciąg odwrotności jego wyrazów jest zbieżny do zera i na odwrót, jeżeli ciąg wyjściowy o wyrazach dodatnich jest zbieżny do zera, to ciąg odwrotności jego wyrazów jest rozbieżny do . [ ]1 ∞ [ ]01+

=

b

n _a1_n

+∞

(24)

TWIERDZENIE

Twierdzenie 4:

Twierdzenie 4: o symbolach oznaczonych

o symbolach oznaczonych

i i

Jeżeli , to oraz Jeżeli , to

PRZYKŁAD

Przykład 18:

Oblicz granicę . Rozwiązanie:

Zauważamy, że dla oraz, że .

Z twierdzenia o dwóch ciągach mamy

Czyli z twierdzenia o symbolach oznaczonych otrzymujemy .

PRZYKŁAD

Przykład 19:

Oblicz granicę . Rozwiązanie:

Zauważamy, że ciąg ma wyrazy dodatnie oraz, że . Rzeczywiście nierówność

jest równoważna nierówności , czyli, aby była spełniona definicja granicy wystarczy przyjąć .

Z twierdzenia o symbolach oznaczonych wnioskujemy więc, że .

[ ]

1

0 [ ]

∞

1 | | = 0

lim

n→∞

a

n

lim

n→∞ _{| |}_a1_n

= +∞

∞

lim

n→∞

a

n

=

+−

lim

n→∞ _a1_n

= 0.

lim

n→∞ _{2 +n−1}_n21

2 + n − 1 > n

n

2

_{n ∈ N}

_lim

_n→∞

_{n = +∞}

(2 + n − 1) = +∞.

lim

n→∞

n

2

= 0

lim

n→∞n _{2 +n−1}_n21

lim

n→∞n _{sin ( )}11 n

sin ( )

1 n

lim

n→∞

| sin ( )| = 0

1n

| sin ( ) − 0| < ε

1 n

n >

arcsin ε1

= [

] + 1

n0

_{arcsin ε}1

= +∞

lim

n→∞ _{sin ( )}11 n

(25)

TWIERDZENIE

Twierdzenie 5:

Twierdzenie 5: o symbolach oznaczonych

o symbolach oznaczonych

Niech będzie dowolna liczbą rzeczywistą. Symbolami oznaczonymi są

gdzie symbol oznacza granicę ciągu o wyrazach dodatnich zbieżnego do zera, a symbol granicę ciągu o wyrazach ujemnych zbieżnego do zera.

PRZYKŁAD

Przykład 20:

Oblicz granicę Rozwiązanie:

Przekształcimy wyjściowe wyrażenie graniczne do znanego symbolu oznaczonego

a

[±∞ + a] = ±∞,

[a ⋅ (±∞)] = {

±∞

_∓∞

dla a > 0

_{dla a < 0}

,

[±∞ ⋅ (±∞)] = +∞,

[±∞ ⋅ (∓∞)] = −∞,

[

a

] = 0,

±∞

[ ] = {

a

,

0±

±∞

_∓∞

dla a > 0

_{dla a < 0}

[

∞

a

] = {

∞

,

0 dla a > 0

dla a < 0

[

∞

] = ∞,

[ ]

0

+

_{[ ]}

₀

−

(3 − 2 + n − 4)

lim

n→∞

n

3

n

2

[∞ − ∞ + ∞ − 4]

(3 − 2 + n − 4) =

(3 − +

− ) = [∞ ⋅ (3 − 0 + 0 − 0)] = ∞

lim

n→∞

n

3

n

2

lim

n→∞

n

3 _n2 _n12 _n43

(26)

PRZYKŁAD

Przykład 21:

Oblicz granicę Rozwiązanie: Zauważamy, że . Obliczamy .

PRZYKŁAD

Przykład 22:

Jako pierwszą obliczamy granicę wykładnika w potędze znajdującej się w liczniku

Następnie wykorzystujemy odpowiedni symbol oznaczony do obliczenia granicy . Ostateczne obliczamy granicę

TWIERDZENIE

Twierdzenie 6:

Twierdzenie 6: o symbolach nieoznaczonych

o symbolach nieoznaczonych

Symbolami nieoznaczonymi są , , , , , ,

(

lim

n→∞ n+1 2 n+1

)

n

=

= [

] = ∞

lim

n→∞ n+1 2 n+1

lim

n→∞ n(1+ )1 n2 1+1 n ∞⋅(1+0) 1+0

(

= [

] = ∞

lim

n→∞ n+1 2 n+1

)

n

∞

lim

n→∞ (2n+3) n+4 3−n 4 +3nn3

= [

] =

= [

] =

lim

n→∞ _3−2nn+4 _−∞∞

lim

n→∞ n(1+ ) 4 n n( −2)3 n 1+0 0−2 −21

(2n + 3

= [

] = 0

lim

n→∞

)

n+4 3−2n

∞

−21

= [[ ] = 0.

lim

n→∞ (2n+3) n+4 3−n 4 +3nn3 _∞0

[ ]

0 0

[ ]

∞∞

[0 ⋅ ∞] [∞ − ∞] [

∞

0

]

[ ]

0

[ ].

1

∞

(27)

PRZYKŁAD

Przykład 23:

Wykaż, że symbol jest nieoznaczony. Rozwiązanie:

Wiemy, że oraz .

Obliczamy dwie różne granice, które dają ten sam symbol nieoznaczony , ale różne wyniki końcowe

.

Świadczy to o tym, że nie da się w sposób jednoznaczny określić wartości symbolu .

PRZYKŁAD

Przykład 24:

Wykaż, że symbol jest nieoznaczony. Rozwiązanie:

Znajdziemy dwa ciągi, które dają ten sam symbol graniczny , ale różne wyniki końcowe uzyskane za pomocą prostego przekształcenia algebraicznego

Różne wyniki dowodzą, że nie da się w sposób jednoznaczny określić wartości symbolu .

Twierdzenia pozwalające wyliczać granice ciągów

[0 ⋅ ∞]

n =

= ∞

lim

n→∞

lim

n→∞

n

2

lim

n→∞ _n12

=

lim

n→∞ _n1

= 0

[[0 ⋅ ∞]

⋅ n = [0 ⋅ ∞] =

= 0

lim

n→∞ _n12

lim

n→∞ _n1

⋅

= [0 ⋅ ∞] =

n = ∞

lim

n→∞ _n1

n

2

lim

n→∞

[0 ⋅ ∞]

[∞ − ∞]

( − n) = [∞ − ∞] =

(1 − ) = [∞ ⋅ (1 − 0)] = ∞

lim

n→∞

n

3

lim

n→∞

n

3 _n12

(n − ) = [∞ − ∞] =

( − 1) = [∞ ⋅ (0 − 1)] = −∞.

lim

n→∞

n

3

lim

n→∞

n

3 1_n2

[∞ − ∞]

(28)

TWIERDZENIE

Twierdzenie 7:

Twierdzenie 7: o działaniach arytmetycznych na ciągach zbieżnych

o działaniach arytmetycznych na ciągach zbieżnych

Jeżeli i , to

PRZYKŁAD

Przykład 25:

Korzystamy z twierdzenia o działaniach arytmetycznych na ciągach zbieżnych, otrzymując

PRZYKŁAD

Przykład 26:

Zauważmy, że nie możemy od razu skorzystać z twierdzenia o działaniach arytmetycznych na ciągach zbieżnych, bo ciągi w liczniku i mianowniku są rozbieżne do . Wykonamy najpierw przekształcenie algebraiczne, które pozwoli uzyskać ciągi zbieżne

= a

lim

n→∞

a

n

lim

n→∞

b

n

= b

( + ) = a + b,

lim

n→∞

a

n

b

n

(c ⋅ ) = c ⋅ a dla dowolnego c ∈ R,

lim

n→∞

a

n

( ⋅ ) = a ⋅ b,

lim

n→∞

a

n

b

n

= , b ∈ R ∖ {0}.

lim

n→∞ a_bn_n a_b

( + − 5)

lim

n→∞ _n32 _n2

( + − 5) = [3 ⋅ 0 + 2 ⋅ 0 − 5] = [0 − 5] = −5

lim

n→∞ _n32 _n2

lim

n→∞ (3n+1)(−2n+4)_1−3n−2n2

−∞

=

= [

] = 3

lim

n→∞ (3n+1)(−2n+4)_1−3n−2n2

lim

n→∞ (3+ )(−2+ ) n2 1 n n4 ( − −2) n2 1 n2 3 n (3+0)(−2+0) 0−0−2

(29)

PRZYKŁAD

Przykład 27:

Obliczmy Rozwiązanie:

W liczniku i w mianowniku ułamka, który jest wyrazem naszego ciągu mamy ciągi rozbieżne do , czyli wykonujemy przekształcenie algebraiczne pozwalające uzyskać ciągi zbieżne

Rysunek 19: Interpretacja twierdzenia o dwóch ciągach rozbieżnych do

Rys. 19 przedstawia na jednym wykresie dwa ciągi, z których jeden ma od pewnego miejsca wyrazy większe od drugiego. Na pierwszym wykresie ciąg o wyrazach mniejszych (czerwony) jest rozbieżny do i na podstawia twierdzenia o zachowaniu nierówności w granicy możemy wnioskować, że ciąg o wyrazach większych (niebieski) też musi być rozbieżny do .

Rysunek 20: Interpretacja geometryczna twierdzenia o dwóch ciągach rozbieżnych do

Na Rys. 20 przedstawiony jest ciąg o wyrazach większych (czerwony), który jest rozbieżny do i stąd wnioskujemy, że ciąg o wyrazach mniejszych (niebieski) tez musi być rozbieżny do .

lim

n→∞ 27 +3 +2n 6 _n2 √3 (4n−2) 8 +2n_√n2

+∞

=

= [

] =

lim

n→∞ 27 +3 +2n 6 _n2 √3 (4n−2) 8 +2n_√n2

lim

n→∞ (27+ + ) n6 3 n4 2 n6 √3 n(4− )2 n √n2(8+ )n2

lim

n→∞ n2 _{27+ +}3 n4 2 n6 √3 (4− ) n2 2 n √8+2n 27+0+0 √3 (4−0) 8+0√ 8 2√3 +∞

+∞

−∞

(30)

TWIERDZENIE

Twierdzenie 8:

Twierdzenie 8: o dwóch ciągach

o dwóch ciągach

Jeżeli oraz od pewnego miejsca pomiędzy wyrazami dwóch ciągów zachodzą nierówności , to lub

Jeżeli oraz od pewnego miejsca pomiędzy wyrazami dwóch ciągów zachodzą nierówności , to .

PRZYKŁAD

Przykład 28:

Skorzystamy z twierdzenia o dwóch ciągach i wykorzystamy ograniczenie dla funkcji sinus prawdziwą dla wszystkich naturalnych.

Ponieważ ciąg o wyrazach większych jest rozbieżny do , zatem

PRZYKŁAD

Przykład 29:

Skorzystamy z twierdzenia o dwóch ciągach i będziemy wyraz naszego ciągu ograniczać od dołu. Zauważamy, że każdy wyraz ciągu jest sumą ułamków postaci i składników sumy jest więcej im większe jest , czyli w -tym wyrazie ciągu jest dokładnie składników. Aby ograniczyć tę sumę od dołu wybieramy składnik najmniejszy i mnożymy go przez liczbę składników otrzymując

Ponieważ ciąg o wyrazach mniejszych jest rozbieżny do , więc .

= +∞

lim

n→∞

a

n

a

n

≤

b

n

= +∞

lim

n→∞

b

n

= −∞

lim

n→∞

b

n

a

n

≤

b

n

= −∞

lim

n→∞

a

n

(3 sin n − 5) ⋅

lim

n→∞

n

3

sin n ≤ 1

n

(3 sin n − 5) ⋅

n

3

≤ (3 ⋅ 1 − 5) ⋅

_n

3

= −2 ≤ −n

_n

3 n→∞

_⟶

−∞

lim

n→∞

(3 sin n − 5) ⋅

n

3

= −∞

(

+

+ ⋯ +

)

lim

n→∞ _√1₁ _√1₂ _√1_n 1 k √

n

+∞

n→∞

⟵

√

n

=

1

⋅ n ≤

+

+ ⋯ +

n √ √11 √12 √1n

+∞

lim

n→∞

(

_√1₁

+

_√1₂

+ ⋯ +

_√1_n

) = +∞

(31)

PRZYKŁAD

Przykład 30:

Oblicz granicę .

Rozwiązanie:

Skorzystamy z twierdzenia i ograniczenia dla funkcji cosinus dla wszystkich naturalnych. Otrzymujemy ograniczenie od dołu dla wyrazów naszego ciągu

Ponieważ zachodzi kolejne ograniczenie

oraz ciąg o wyrazach mniejszych jest rozbieżny do , to .

PRZYKŁAD

Przykład 31:

Oblicz granicę .

Rozwiązanie:

Skorzystamy z twierdzenia o dwóch ciągach i zauważamy, że . Otrzymujemy ograniczenie od góry wyrazu naszego ciągu

Ponieważ ciąg o wyrazach większych jest rozbieżny do , to .

Rysunek 21: Interpretacja geometryczna twierdzenia o trzech ciągach

Rys. 21 przedstawia na jednym wykresie trzy ciągi, z których jeden (czerwony) ma wyrazy od pewnego miejsca leżące pomiędzy wyrazami dwóch innych ciągów (niebieskiego i zielonego), przy czym ciągi o wyrazach skrajnych są zbieżne do tej samej granicy właściwej . Ponieważ prawie wszystkie wyrazy ciągów skrajnych leżą w przedziale , a wyrazy ciągu środkowego leżą pomiędzy wyrazami ciągów skrajnych, to z konieczności w przedziale leża prawie wszystkie wyrazy ciągu środkowego, czyli ma on taką sama granicę .

lim

n→∞ (2+cos )n 2_n3 n−3

cos n ≥ −1

n

=

≤

.

n2 (1− )3 n n3 n(1− )3 n (2−1)n3 n−3 (2+cos ) n2_n3 n−3

+∞

n→∞

⟵

n

2

≤

n2 (1− )3 n

+∞

lim

n→∞ (2+cos )n

= +∞

2_n3 n−3

lim

n→∞ ((−1 −2)) n _n2 n+1

(−1 ≤ 1

)

n

≤

=

−∞

((−1 −2))n _n2 n+1 (1−2)n 2 n+1 −n 2 n+1

⟶

n→∞

−∞

lim

n→∞ ((−1 −2))

= −∞

n _n2 n+1

g

(g − ϵ, g + ϵ)

g

(32)

TWIERDZENIE

Twierdzenie 9:

Twierdzenie 9: o trzech ciągach

o trzech ciągach

Jeżeli oraz od pewnego miejsca zachodzi nierównośc pomiędzy wyrazami trzech ciągów , to ciąg jest zbieżny i .

PRZYKŁAD

Przykład 32:

Skorzystamy z twierdzenia o trzech ciągach szacując wyraz naszego ciągu od dołu i od góry tak, aby otrzymać ciągi o tej samej granicy i wykorzystujemy znane ograniczenia funkcji sinus i cosinus i , które są prawdziwe dla każdego naturalnego

Zatem wnioskujemy, że

PRZYKŁAD

Przykład 33:

Skorzystamy z twierdzenia o trzech ciągach i szacowania sumy od góry przez największy składnik pomnożony przez liczbę składników, a od dołu przez najmniejszy składnik pomnożony przez liczbę składników.

Zauważmy, że oraz

Ponieważ skrajne ciągi mają tę samą granicę, to .

Rysunek 22: Interpretacja geometryczna granicy iloczynu ciągów, z których jeden jest zbieżny do zera, a drugi jest ograniczony

= g =

lim

n→∞

a

n

lim

n→∞

c

n

≤ ≤

a

n

b

n

c

n

( )

b

n

lim

n→∞

b

n

= g

lim

n→∞ _{2+n sin}n2+n−cos_√_n₊₃n2_n2

−1 ≤ sin

√

n

≤ 1

−1 ≤ cos

n

2

≤ 1

n

=

≤

=

1 3

⟵

n→∞ n2(1+ − )1 n _n21 ( + +3) n2 2 n2 1 n +n−1 n2 2+n+3n2 n+n−cos 2 _n2 2+n sin√n+3n2 n+n+1 2 2−n+3n2 (1+ + ) n2 1 n _n21 ( − +3) n2 2 n2 1 n

⟶

n→∞ 1 3

=

lim

n→∞ n+n−cos 2 _n2 2+n sin√n+3n2 1₃

(

+

+ ⋯ +

)

lim

n→∞ _√_n12₊₂ _√_n21_+2⋅2 _√_n21_+2⋅n

n ⋅

1

≤ (

+

+ ⋯ +

) ≤ n ⋅

+2⋅n n2 √ _√n12+2 _√_n21_+2⋅2 _√_n21_+2⋅n _√_n12₊₂

=

= [

] = 1

lim

n→∞ _√_n2n_+2⋅n

lim

n→∞ n n⋅ 1+2 n √ 1 1+0 √

lim

n→∞ _√nn2+2

=

lim

n→∞ _{n⋅ 1+}n 2

= 1

n2 √

(

+

+ ⋯ +

) = 1

lim

n→∞ _√_n12₊₂ _√_n21_+2⋅2 _√_n21_+2⋅n

(33)

Rys. 22 przedstawia wykres ciągu zbieżnego do zera (niebieski) oraz wykres ciągu ograniczonego (czerwony) i wykres ciągu, którego każdy wyraz jest iloczynem wyrazów poprzednich ciągów (zielony). Ponieważ prawie wszystkie wyrazy ciągu zbieżnego do zera leżą w przedziale i wszystkie wyrazy ciągu ograniczonego lezą w przedziale , to prawie wszystkie wyrazy iloczynu tych ciągów leżą w przedziale . Z dowolności liczby otrzymujemy, że liczba może też być dowolnie mała, czyli liczba zero jest granicą iloczynu wyjściowych ciągów.

TWIERDZENIE

Twierdzenie 10:

Twierdzenie 10: o iloczynie ciągu zbieżnego do zera i ciągu ograniczonego

o iloczynie ciągu zbieżnego do zera i ciągu ograniczonego

Jeżeli i ciąg jest ograniczony, to

PRZYKŁAD

Przykład 34:

Obliczmy .

Rozwiązanie:

skorzystamy z twierdzenia o iloczynie ciągu zbieżnego do zera i ciągu ograniczonego otrzymując

Zatem .

Granice pewnych ciągów specjalnych