Obliczenie siy krytycznej za pomoca Mathcada, porwnanie z wynikami Algora

Stateczność ramy drewnianej o 2 różnych przekrojach prętów, obciążonej siłą skupioną

ORIGIN := 1 - Ustawienie sposobu numeracji wierszy i kolumn macierzy

E := 10GPa - Moduł Younga drewna

Wymiary przekrojów

a₁ := 7cm b₁ := 7cm

a₂ := 7cm b₂ := 10cm

Parametry pomocnicze:

Lss := 3 - Liczba stopni swobody węzła

Le:= 5 - Liczba elementów

Lw:= 6 - Liczba węzłów

Lr:= Lss Lw× - Liczba równań

Ko_{Lr Lr,} := 0 Deklaracja globalnej macierzy sztywności i wypełnienie jej zerami

Ponieważ MathCad nie pozwala przechowywać w jednej macierzy składowych wyrażonych w różnych jednostkach to mamy do wyboru 2 mozliwości:

- nie zapisywać jednostek w których wyrażone są te składowe

- przekształcić tak te składowe, aby były jednolite (wyrażone w jednakowych jednostkach miary) Wybieram 2 sposób i przekształcam niewiadome występujące w macierzach następująco

( l - oznacza tu dowolną stałą o wymiarze długości) :

uzi l φi= × uzj l φj= × Mi l Ti= × Mj l Tj= × λ2 L

2_×A

J

= η L

l

=

Wszystkie poszukiwane przemieszczenia są więc przesunięciami, a węzłowe wielkości statyczne - siłami. Macierz sztywności zmieni sie więc do postaci, którą MathCad akceptuje:

Fxi Fyi Ti Fxj Fjy Tj æç ç ç ç ç ç ç çè ö÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ø E J× L3 λ2 0 0 λ2 -0 0 0 12 6η 0 12 -6η 0 6η 4η2 0 6η -2η2 λ2 -0 0 λ2 0 0 0 12 -6η -0 12 6η -0 6η 2η2 0 6η -4η2 æ ç ç ç ç ç ç ç ç ç è ö ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ø S L 0 0 0 0 0 0 0 1.2 0.1η 0 1.2 -0.1η 0 0.1η 2 15η 2 0 0.1 - η 1 -30η 2 0 0 0 0 0 0 0 1.2 -0.1 - η 0 1.2 0.1 - η 0 0.1η 1 -30η 2 0 0.1 - η 2 15η 2 æ ç ç ç ç ç ç ç ç ç ç è ö ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ø × + é ê ê ê ê ê ê ê ê ê ê ë ù ú ú ú ú ú ú ú ú ú ú û uxi uyi uzi uxj uyj uzj æç ç ç ç ç ç ç çè ö÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ø × =

Funkcja LBM - Lokuj Blok Macierzy, używana przy agregacji macierzy sztywności i wektora obciążeń termicznych LBM A B( , , w, k) A_{w i+ , k j+} ¬B_{1 i+ , 1 j+} j 0Î .. cols B( ) 1 -for i 0Î .. rows B( ) 1 -for A :=

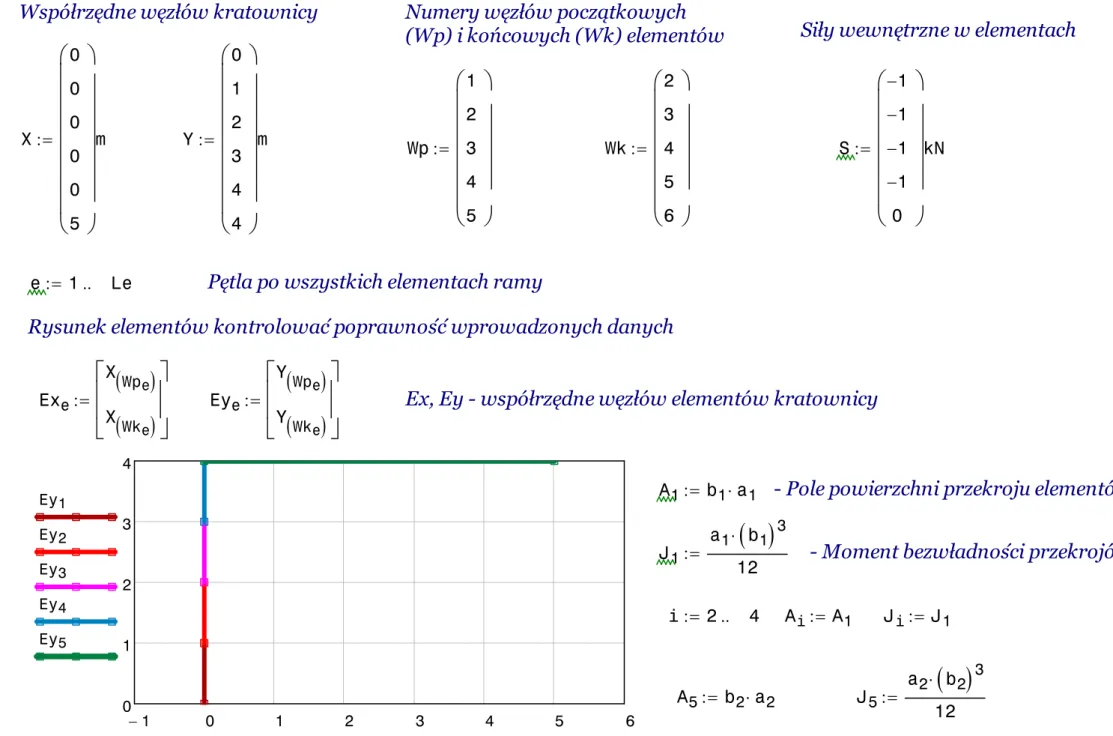
Współrzędne węzłów kratownicy Numery węzłów początkowych

(Wp) i końcowych (Wk) elementów Siły wewnętrzne w elementach

X 0 0 0 0 0 5 æç ç ç ç ç ç ç çè ö÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ø m := Y 0 1 2 3 4 4 æç ç ç ç ç ç ç çè ö÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ø m := _Wp 1 2 3 4 5 æ ç ç ç ç ç ç è ö ÷ ÷ ÷ ÷ ÷ ÷ ø := Wk 2 3 4 5 6 æ ç ç ç ç ç ç è ö ÷ ÷ ÷ ÷ ÷ ÷ ø := S 1 -1 -1 -1 -0 æ ç ç ç ç ç ç è ö ÷ ÷ ÷ ÷ ÷ ÷ ø kN :=

e := 1.. Le Pętla po wszystkich elementach ramy

Rysunek elementów kontrolować poprawność wprowadzonych danych

Ex_e X _Wp e

( )

X _Wk e

( )

é ê ê ë ù ú ú û := Ey_e Y _Wp e

( )

Y _Wk e

( )

é ê ê ë ù ú ú û

:= Ex, Ey - współrzędne węzłów elementów kratownicy

1 - 0 1 2 3 4 5 6 0 1 2 3 4 Ey₁ Ey2 Ey3 Ey4 Ey5 Ex1, Ex2, Ex3, Ex4, Ex5

A₁ := b₁×a₁ - Pole powierzchni przekroju elementów J₁ a1

( )

b1

3

× 12

:= - Moment bezwładności przekrojów

i := 2.. 4 A_i := A₁ J_i := J₁ A₅ := b₂×a₂ J₅ a2

( )

b2 3 × 12 :=

Wielkości pomocnicze do wyliczania składowych macierzy sztywności elementów ramy Lx_e X _Wk e

( )

-X

( )

Wp_e := Ly_e Y _Wk e

( )

-Y

( )

Wp_e := L_e :=

( )

Lx_e 2+

( )

Ly_e 2 Lx 1 1 2 3 4 5 0.000 0.000 0.000 0.000 5.000 m = Ly 1 1 2 3 4 5 1.000 1.000 1.000 1.000 0.000 m = L 1 1 2 3 4 5 1.000 1.000 1.000 1.000 5.000 m = A 1 1 2 3 4 5 49.000 49.000 49.000 49.000 70.000 cm2 × = J 1 1 2 3 4 5 200.083 200.083 200.083 200.083 583.333 cm4 × = η_e Le l := λ2_e

( )

Le 2 _A e × J_e := μ_e E J× e L_e

( )

3 := κ_e Se L_e := η 1 1 2 3 4 5 1.000 1.000 1.000 1.000 5.000 = λ2 1 1 2 3 4 5 2448.980 2448.980 2448.980 2448.980 30000.000 = μ 1 1 2 3 4 5 20008.333 20008.333 20008.333 20008.333 466.667 N m × = κ 1 1 2 3 4 5 -1000.000 -1000.000 -1000.000 -1000.000 0.000 N m × =

Bloki macierzy sztywności elementu ramowego w lokalnym układzie współrzednych K11_e μ_e λ2_e 0 0 0 12 6 η_e 0 6 η_e 4 η

( )

_e 2 éê ê ê êë ùú ú ú úû × := K12_e μ_e λ2_e -0 0 0 12 -6 - η_e 0 6 η_e 2 η

( )

_e 2 éê ê ê êë ùú ú ú úû × := K22_e μ_e λ2_e 0 0 0 12 6 - η_e 0 6 - η_e 4 η

( )

_e 2 éê ê ê êë ùú ú ú úû × :=

Macierz sztywności elementu zapisana z użyciem bloków

K K11 K21 K12 K22 æ ç è ö ÷ ø = K21 = K12T

Bloki macierzy geometrycznych elementu ramowego w lokalnym układzie współrzednych

G11_e κ_e 0 0 0 0 1.2 0.1 η_e 0 0.1 η_e 2 15

( )

ηe 2 é ê ê ê ê ë ù ú ú ú ú û × := G12_e κ_e 0 0 0 0 1.2 -0.1 - η_e 0 0.1 η_e 1 -30

( )

ηe 2 é ê ê ê ê ë ù ú ú ú ú û × := G22_e κ_e 0 0 0 0 1.2 0.1 - η_e 0 0.1 - η_e 2 15

( )

ηe 2 é ê ê ê ê ë ù ú ú ú ú û × :=

Macierz geometryczna elementu zapisana z użyciem bloków

G G11 G21 G12 G22 æ ç è ö ÷ ø = G21 = G12T

Macierze obrotu do globalnego układu współrzednych c_e Lxe L_e := s_e Lye L_e := R_e c_e s_e 0 s_e -c_e 0 0 0 1 æ ç ç ç è ö ÷ ÷ ÷ ø := R₁ 0 1 0 1 -0 0 0 0 1 æç ç ç è ö÷ ÷ ÷ ø = R₂ 0 1 0 1 -0 0 0 0 1 æç ç ç è ö÷ ÷ ÷ ø =

Transformacja macierzy sztywności i macierzy geometrycznych elementu 1 do globalnego układu współrzędnych.

Uwaga!

Macierzy elementu 5 można nie transformować bo kąt obrotu jest równy 0 Macierze elementów 1..4 są identyczne

K11_e:= R_e×K11_e×R_eT K12_e:= R_e×K12_e×R_eT K22_e:= R_e×K22_e×R_eT G11_e:= R_e×G11_e×R_eT G12_e:= R_e×G12_e×R_eT G22_e:= R_e×G22_e×R_eT

Mimo, że nie jest to potrzebne w dalszych obliczeniach, można pokazać bloki macierzy wszystkich elementów K11₁ 240.1 0 120.05 -0 49000 0 120.05 -0 80.033 æç ç ç è ö÷ ÷ ÷ ø kN m × = K11₅ 14000 0 0 0 5.6 14 0 14 46.667 æç ç ç è ö÷ ÷ ÷ ø kN m × = K12₁ 240.1 -0 120.05 0 49000 -0 120.05 -0 40.017 æç ç ç è ö÷ ÷ ÷ ø kN m × = K12₅ 14000 -0 0 0 5.6 -14 -0 14 23.333 æç ç ç è ö÷ ÷ ÷ ø kN m × = K22₁ 240.1 0 120.05 0 49000 0 120.05 0 80.033 æç ç ç è ö÷ ÷ ÷ ø kN m × = K22₅ 14000 0 0 0 5.6 14 -0 14 -46.667 æç ç ç è ö÷ ÷ ÷ ø kN m × = G11₁ 1.2 -0 0.1 0 0 0 0.1 0 0.133 -æç ç ç è ö÷ ÷ ÷ ø kN m × = G12₁ 1.2 0 0.1 -0 0 0 0.1 0 0.033 æç ç ç è ö÷ ÷ ÷ ø kN m × = G22₁ 1.2 -0 0.1 -0 0 0 0.1 -0 0.133 -æç ç ç è ö÷ ÷ ÷ ø kN m × = G11₅ 0 0 0 0 0 0 0 0 0 æç ç ç è ö÷ ÷ ÷ ø kN m × = G12₅ 0 0 0 0 0 0 0 0 0 æç ç ç è ö÷ ÷ ÷ ø kN m × = G22₅ 0 0 0 0 0 0 0 0 0 æç ç ç è ö÷ ÷ ÷ ø kN m × =

Agregacja, czyli dodawanie bloków macierzy sztywności elementów do macierzy globalnej

n_e := Lss Wp× _e-2 k_e := Lss Wk× _e-2 <--- numery stopni swobody węzłów początkowych (n_e) i końcowych (k_e)

nT = (1 4 7 10 13 ) kT = (4 7 10 13 16 ) K e LBM Ko K11

(

, _e, n_e, n_e

)

+LBM Ko K22

(

, _e, k_e, k_e

)

(

)

+LBM Ko K12

(

, _e, n_e, k_e

)

+LBM Ko K12

(

, _eT , k_e, n_e

)

é ë ùû

å

:= G e LBM Ko G11

(

, _e, n_e, n_e

)

+LBM Ko G22

(

, _e, k_e, k_e

)

(

)

+LBM Ko G12

(

, _e, n_e, k_e

)

+LBM Ko G12

(

, _eT , k_e, n_e

)

é ë ùû

å

:= K 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 240.1 0.0 -120.1 -240.1 0.0 -120.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 49000.0 0.0 0.0 -49000.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -120.1 0.0 80.0 120.1 0.0 40.0 0.0 0.0 0.0 0.0 0.0 0.0 -240.1 0.0 120.1 480.2 0.0 0.0 -240.1 0.0 -120.1 0.0 0.0 0.0 0.0 -49000.0 0.0 0.0 98000.0 0.0 0.0 -49000.0 0.0 0.0 0.0 0.0 -120.1 0.0 40.0 0.0 0.0 160.1 120.1 0.0 40.0 0.0 0.0 0.0 0.0 0.0 0.0 -240.1 0.0 120.1 480.2 0.0 0.0 -240.1 0.0 -120.1 0.0 0.0 0.0 0.0 -49000.0 0.0 0.0 98000.0 0.0 0.0 -49000.0 0.0 0.0 0.0 0.0 -120.1 0.0 40.0 0.0 0.0 160.1 120.1 0.0 40.0 0.0 0.0 0.0 0.0 0.0 0.0 -240.1 0.0 120.1 480.2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -49000.0 0.0 0.0 98000.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -120.1 0.0 40.0 0.0 0.0 160.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -240.1 0.0 120.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -49000.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 -120.1 0.0 40.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... kN m × =

G 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 -1.2 0.0 0.1 1.2 0.0 0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.1 0.0 -0.1 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.2 0.0 -0.1 -2.4 0.0 0.0 1.2 0.0 0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.1 0.0 0.0 0.0 0.0 -0.3 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.2 0.0 -0.1 -2.4 0.0 0.0 1.2 0.0 0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.1 0.0 0.0 0.0 0.0 -0.3 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.2 0.0 -0.1 -2.4 0.0 0.0 1.2 0.0 0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.1 0.0 0.0 0.0 0.0 -0.3 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.2 0.0 -0.1 -1.2 0.0 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.1 0.0 0.0 -0.1 0.0 -0.1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 kN m × =

Globalna macierz sztywności K i macierz geometryczna G bez uwzględnienia warunków brzegowych jest osobliwa tzn. |K|=0 , |G|=0

Aby obliczyć wyznacznik macierzy, której elementy nie są liczbami bezwymiarowymi musimy macierz pomnożyć przez odwrotność jednostek aby doprowadzić elementy do postaci bezwymiarowej - to jest wymóg MatCada.

Zamiast zera wyznacznik może być "bardzo małą" liczbą ze względu na niedostateczną dokładność wyrazów macierzy sztywności.

K 1m kN × = 0.000 10´ 0 G 1m kN × = 0.000 10´ 0

Kopiowanie Macierzy K przed modyfikacją uwzględniającą warunki brzegowe

Ko:= K Go:= G

Uwzględnienie warunków brzegowych

Lwb := 5 - liczba warunków brzegowych

s 1 2 3 16 17 æ ç ç ç ç ç ç è ö ÷ ÷ ÷ ÷ ÷ ÷ ø

:= - globalne numery przemieszczeń węzłów blokowanych na podporach

i := 1.. Lr j := 1.. Lwb Ko_s j, i:= 0 Gosj, i:= 0 zerowanie wierszy Ko_{i s} j , := 0 Goi s, _j:= 0 zerowanie kolumn

wstawianie jedności na przekątną macierzy sztywności Ko_s j, sj 1 kN m := Ko 1× m kN 5.882 10 39 ´

= - wyznacznik macierzy K_o jest zawsze większy od zera, |K_o|> 0

Go 1× m

kN 0.000 10

0

´

Ko 1 2 3 4 5 6 7 8 9 10 11 12 13 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 480.2 0 0 -240.1 0 -120.1 0 0 0 0 0 0 0 0 98000 0 0 -49000 0 0 0 0 0 0 0 0 0 0 160.1 120.1 0 40 0 0 0 0 0 0 0 -240.1 0 120.1 480.2 0 0 -240.1 0 -120.1 0 0 0 0 0 -49000 0 0 98000 0 0 -49000 0 0 0 0 0 -120.1 0 40 0 0 160.1 120.1 0 40 0 0 0 0 0 0 0 -240.1 0 120.1 480.2 0 0 -240.1 0 0 0 0 0 0 0 -49000 0 0 98000 0 0 0 0 0 0 0 0 -120.1 0 40 0 0 160.1 120.1 0 0 0 0 0 0 0 0 0 -240.1 0 120.1 14240.1 0 0 0 0 0 0 0 0 0 0 -49000 0 0 0 0 0 0 0 0 0 0 0 -120.1 0 40 ... kN m × = Go 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -2.4 0 0 1.2 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0.267 -0.1 0 0.033 0 0 0 0 0 0 0 0 0 1.2 0 -0.1 -2.4 0 0 1.2 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0.033 0 0 -0.267 -0.1 0 0.033 0 0 0 0 0 0 0 0 0 1.2 0 -0.1 -2.4 0 0 1.2 0 0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.1 0 0.033 0 0 -0.267 -0.1 0 0.033 0 0 0 0 0 0 0 0 0 1.2 0 -0.1 -1.2 0 -0.1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ... kN m × =

Ko σ Go+ × = 0 - warunek niejednoznacznosci przemieszczeń, czyli mozliwość utraty stateczności KG σ( ) (Ko σ Go+ × ) m

kN × :=

Oszacowanie wartości siły krytycznej "z góry" i "z dołu" N := 1000 i := 1.. N σ_i := i 0.1× W_i := KG σ

( )

_i P1 π 2_{×E J} 1 × 0.5 Y× ₅

(

)

2 := 0 10 20 30 40 50 60 70 80 90 100 1 -1 2 3 4 5 6 Wi 1039 σi P2 π 2_{×E J} 1 × 0.699 Y× ₅

(

)

2 := P1 = 49.369 kN× P2 = 25.260 kN×

N1:= 39370 N2:= 39380

i := N1.. N2 σ_i := i 0.001× W_i := KG σ

( )

_i

Siła krytyczna (pierwsza wartość własna) ma przybliżoną wartość Pkr=39,372 kN 39.37 39.371 39.372 39.373 39.374 39.375 39.376 39.377 39.378 39.379 39.38 4 -3 -2 -1 -1 2 W_i 1035 σi

Siła krytyczna (pierwsza wartość własna) wyliczona za pomocą Algora, przy podziale pręta poziomego i pionowego na 10 elementów Pkr=34,4645 kN

N1:= 86000 N2:= 87000

i := N1.. N2 σ_i := i 0.001× W_i := KG σ

( )

_i

Druga wartość własna ma przybliżoną wartość σ2=86,55 kN 86 86.1 86.2 86.3 86.4 86.5 86.6 86.7 86.8 86.9 87 200 -150 -100 -50 -50 100 Wi 1035 σi

Druga wartość własna wyliczona za pomocą Algora, przy podziale pręta poziomego i pionowego na 10 elementów