Odkrywanie struktur ukrytych w danych czyli eksploracja danych Final

Dwie metody

• Klasyczna metoda histogramu jako narzędzie

do postawienia hipotezy, jaki rozkład

prawdopodobieństwa pasuje do danych

• Indukcja drzewa decyzyjnego jako metoda

wykrycia klasyfikatora ukrytego w danych

trenujących

Przykład eksploracji danych o naturze

statystycznej

Próba 1 wartości zmiennej losowej ‘odległość’

21 5 36 54 7 14 43 7 3 24 22 41 56 2 10 39 48 2 43 14 36 29 49 8 42 35 23 35 41 28 56 30 22 9 46 15 58 28 21 56 37 40 14 55 41 36 23 55 53 52 69 35 51 62 41 15 65 15 29 26 60 29 22 70 44 42 16 48 77 44 29 22 28 41 48 3 54 55 42 68 30 29 11 46 17 69 68 4 76 28 31 32 47 56 21 55 36 52 48 83

Czy można prognozować procent odległości powyżej 40 km? Próba 2 wartości zmiennej losowej ‘odległość’

51 8 47 36 28 31 51 36 26 56 3 11 74 21 56 30 67 56 60 44 55 39 42 22 14 39 3 48 23 38 48 46 77 56 26 6 42 22 48 70 15 39 30 38 51 38 19 15 43 59 55 38 52 69 26 35 37 52 66 55 27 44 21 58 55 29 15 22 16 12 36 48 37 29 67 22 35 28 54 8 3 17 43 31 28 30 36 9 65 2 7 21 4 30 83 29 14 47 36 50

Przykład dyskretnej zmiennej

losowej

Rzut kostką

k : X  {1, 2, 3, 4, 5, 6}

Dla i {1, 2, 3, 4, 5, 6}

Pr(k = i) = 1/6

Drugi przykład dyskretnej zmiennej

losowej

Dzienna sprzedaż jednostek towaru x w

pewnym sklepie.

Przykład ciągłej zmiennej losowej

Odległość miejsca zamówienia taksówki

od zajezdni.

Konstrukcja histogramu danych ciągłych

 Posortuj dane.

 Podziel posortowane dane na przedziały (w przypadku 100 danych

powszechną praktyką jest wzięcie od 10 do 15 przedziałów);

jeszcze bardziej powszechną praktyką jest branie takich

przedziałów, że przypada co najmniej od 5 do 8 danych na

przedział. W naszym przypadku po prostu bierzemy przedziały

potencjalnie po 7 danych: [0,7) [7,14) [14,21) [21,28) [28,35)

[35,42) [42,49) [49,56) [56,63) [63,70) [70,77) [77,84)

 oblicz, ile danych wpada do pierwszego przedziału

ile danych wpada do drugiego przedziału

…

ile danych wpada do ostatniego przedziału

to jest właśnie histogram początkowy

 łączymy przylegające przedziały, do których wpadło mniej niż 5

danych i dostajemy wynikowy histogram.

Wynikowe histogramy

Nr. przedziału [lewy kraniec _{prawy kraniec)} Liczba danych

0 0 7 6 1 7 14 7 2 14 21 8 3 21 28 11 4 28 35 13 5 35 42 15 6 42 49 14 7 49 56 11 8 56 63 7 9 63 70 5 10 70 77 2 11 77 84 2

Wynikowy histogram po złączeniu przedziałów

Nr. przedziału [lewy kraniec prawy kraniec) Liczba danych

0 0 7 6 1 7 14 7 2 14 21 8 3 21 28 11 4 28 35 13 5 35 42 15 6 42 49 14 7 49 56 11 8 56 63 7 9 63 999 9

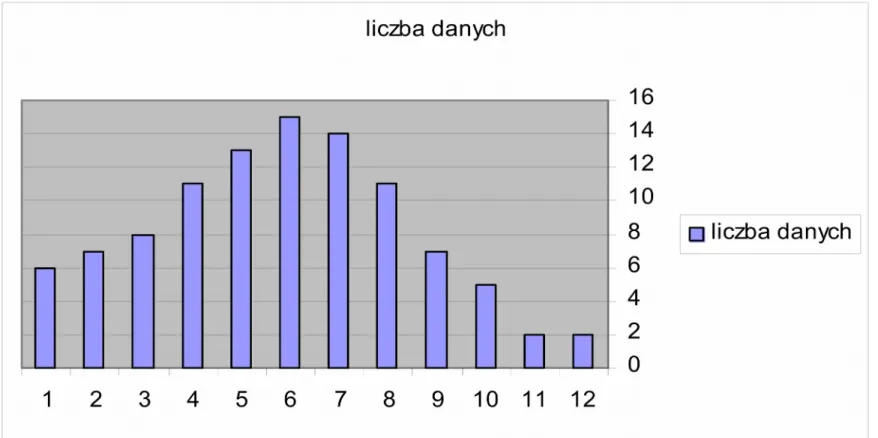
Wykres słupkowy histogramu

1 - przedział [0,7) Pasujący do danych rozkład

2 - przedział [7,14) itd. itd. prawdopodobieństwa to prawo

ukryte w danych

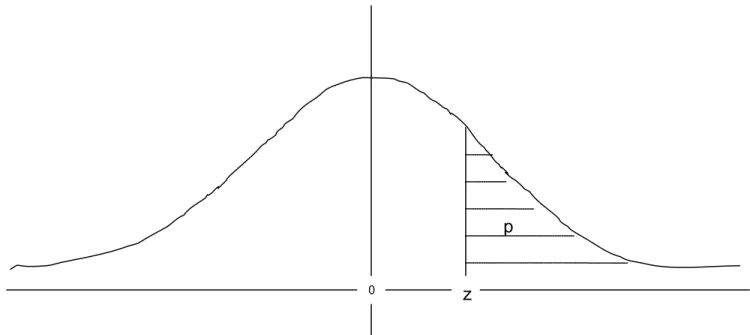
Wykres gęstości standaryzowanego rozkładu normalnego i

interpretacja powierzchni pod krzywą

Cała powierzchnia pod krzywą = 1 = 100% z=0.1787 – standaryzowana wartość 40-stu

p – prawdopodobieństwo, że zmienna losowa przyjmie wartość > 40 Wyliczone z tablic statystycznych p = 0.4291

Prognoza procentu odległości > 40 km – 42.9%

0

p

Eksploracja danych o naturze

kombinatorycznej

Przykład 1

x n k klasyfikacja 1 8 16 1 2 10 20 1 3 6 11 0 4 6 12 1 5 5 3 0 6 4 7 0 7 11 22 1 8 20 6 0 9 9 18 1 10 45 90 1 11 1 2 1 12 5 10 1 13 8 5 0 14 8 4 0 15 4 8 1 16 12 24 ? 17 10 15 ? . .

Przykład 2

x n k klasyfikacja 1 8 16 1 2 10 20 1 3 6 11 0 4 6 12 1 5 5 3 1 6 4 7 0 7 11 22 0 8 20 6 1 9 9 18 0 10 45 90 0 11 1 2 0 12 5 10 0 13 8 5 0 14 8 4 1 15 4 8 1 16 12 24 ?

Przykład 3

x indeks Wartość Klasyfikacja 1 1 15 Drugi 2 2 9 Pierwszy 3 3 4 Pierwszy 4 4 20 Trzeci 5 5 11 Pierwszy 6 6 15 Drugi 7 7 21 Trzeci 8 8 18 Trzeci 9 9 13 Pierwszy 10 10 17 Trzeci 11 11 2 Pierwszy 12 12 12 Pierwszy 13 13 14 Pierwszy 14 14 32 Trzeci 15 15 28 Trzeci 16 16 1 Pierwszy 17 17 10 Pierwszy 18 18 18 ?

Algorytm uczenia

wejście: pewien zbiór treningowy

.

.

. działanie

.

.

wyjście: hipoteza ogólnej klasyfikacji dowolnego

przykładu do jednej z rozważanych

Kolejny przykład – tabela stanów pogody

x aura temperatura wilgotność wiatr Klasyfikacja

1 _{słoneczna ciepła duża słaby} 0

2 _{słoneczna ciepła duża silny} 0

3 _{pochmurna ciepła duża słaby} 1

4 _{deszczowa umiarkowana duża słaby} 1

5 _{deszczowa zimna normalna słaby} 1

6 _{deszczowa zimna normalna silny} 0

7 pochmurna zimna normalna silny 1

8 _{słoneczna umiarkowana duża słaby} 0

9 _{słoneczna zimna normalna słaby} 1

10 _{deszczowa umiarkowana normalna słaby} 1

11 _{słoneczna umiarkowana normalna silny} 1

12 pochmurna umiarkowana duża silny 1

13 _{pochmurna ciepła normalna słaby} 1

14 _{deszczowa umiarkowana duża silny} 0

Testy

 słoneczna gdy atrybutem aura obiektu x jest słoneczna

t

aura

(x) =  pochmurna gdy atrybutem aura obiektu x jest pochmurna

 deszczowa gdy atrybutem aura obiektu x jest deszczowa

Podział zbioru treningowego przez test

Każdy test generuje pewien podział zbioru treningowego. Każdy

zbiór tego podziału dzieli się na elementy poszczególnych kategorii.

Dla testu t

aura

otrzymujemy trzy podziały:

(a)podział obiektów x zbioru treningowego z atrybutem aura =

słoneczna na te zakwalifikowane do kategorii 0 i na te

zakwalifikowane do kategorii 1

(b)podział obiektów x zbioru treningowego z atrybutem aura =

pochmurna na te zakwalifikowane do kategorii 0 i na te

zakwalifikowane do kategorii 1

(c)podział obiektów x zbioru treningowego z atrybutem aura =

deszczowa na te zakwalifikowane do kategorii 0 i na te

Entropia podziału

E =



-p

i

*log(p

i

)

i przebiegające kategorie.

p

i

– prawdopodobieństwo wylosowania elementu kategorii nr. i

Entropia podziału rozpiętego na skończonym

zbiorze

X = A

1

A

2

 . . . A

n

E =  -(|A

i

|/|X|) * log(|A

i

|/|X|)

1 i  n

Ułamek |A

i

|/|X| można interpretować jako

prawdopodobieństwo wylosowania elementu kategorii nr. i ze

zbioru X.

Entropia testu względem zbioru treningowego

Przykład – entropia testu t

aura

ze względu na nasz zbiór

treningowy stanów pogody

Dla testu t

aura

dostajemy trzy podziały:

(a) podział obiektów x zbioru treningowego z atrybutem aura =

słoneczna na te zakwalifikowane do kategorii 0 i na te

zakwalifikowane do kategorii 1,

(b) podział obiektów x zbioru treningowego z atrybutem aura =

pochmurna na te zakwalifikowane do kategorii 0 i na te

zakwalifikowane do kategorii 1,

(c) podział obiektów x zbioru treningowego z atrybutem aura =

deszczowa na te zakwalifikowane do kategorii 0 i na te

Entropia testu względem zbioru treningowego

Entropia testu t

aura

względem zbioru treningowego stanów

pogody to suma ważona:

entropia podziału (a)stosunek liczności zbioru na którym rozpięty jest

podział (a) do liczności całego zbioru treningowego

+

entropia podziału (b)stosunek liczności zbioru na którym rozpięty jest

podział (b) do liczności całego zbioru treningowego

+

entropia podziału (c)stosunek liczności zbioru na którym rozpięty jest

podział (c) do liczności całego zbioru treningowego.

Przykład

t1

Przykład drzewa decyzyjnego dla zbioru treningowego stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14} {1,2,8,9,11} słoneczna t_wilgotność normalna {9,11} 1 duża {1,2,8} 0 pochmurna {3,7,12,13} 1 deszczowa {4,5,6,10,14} t_wiatr słaby {4,5,10} 1 silny {6,14} 0

Idea algorytmu indukcji drzew decyzyjnych

buduj (T, S, k) :

jeżeli

T jest pusty

to

zwróć liść z wpisaną kategorią domniemaną k

w przeciwnym przypadku

jeżeli

w T jest tylko jedna kategoria

to

zwróć liść z wpisaną tą jedyną w

T kategorią

w przeciwnym przypadku

jeżeli

S jest pusty

to

zwróć liść z wpisaną tą kategorią, która jest

najliczniejsza w zbiorze T

w przeciwnym przypadku

// zbiory S i T są niepuste

{

zbudowanie węzła n i jego następników, zwrócenie zbudowanego węzła n jako

wyniku funkcji buduj – szczegóły na następnym slajdzie

};

Zbudowanie węzła n i jego następników, zwrócenie

zbudowanego węzła n jako wyniku funkcji buduj

{ 1. utwórz kolejny węzeł n;

2. ze zbioru S wybierz, wedle przyjętego kryterium wyboru testu, test t i

wpisz go do utworzonego węzła n;

3. jako k przyjmij najliczniejszą w T kategorię;

4. oblicz zbiory treningowe T1, . . ., Tm na które test t dzieli zbiór

treningowy T, gdzie m jest liczbą możliwych wartości testu t;

5. dla wszystkich i = 1, . . . ,m wykonaj

i-ty następnik węzła n := buduj (Ti, S - {t}, k)

//wołanie rekurencyjne

6. zwróć węzeł n jako wynik funkcji buduj;

}

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1

T1={1,2,8,9,11}, 0

słoneczna

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11}

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8}

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13}

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13} 1

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13} 1 deszczowa T3={4,5,6,10,14} buduj(T3,{ttemperatura,twilgotność, twiatr}, 1)

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13} 1 deszczowa T3={4,5,6,10,14} twiatr słaby T31={4,5,10} buduj(T31,{ttemperatura,twilgotność},1)

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13} 1 deszczowa T3={4,5,6,10,14} twiatr słaby T31={4,5,10} 1

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13} 1 deszczowa T3={4,5,6,10,14} twiatr słaby T31={4,5,10} 1 silny T32={6,14} buduj(T32,{ttemperatura, twilgotność},0)

Wykonanie algorytmu buduj na zbiorze treningowym stanów pogody

taura {1,2,3,4,5,6,7,8,9,10,11,12,13,14}, 1 T1={1,2,8,9,11}, 0 słoneczna twilgotność normalna T11= ={9,11} 1 duża T12={1,2,8} 0 pochmurna T2={3,7,12,13} 1 deszczowa T3={4,5,6,10,14} twiatr słaby T31={4,5,10} 1 silny T32={6,14} 0

Podstawowe Pojęcia



zbiór X przykładów – zbiór wszystkich stanów pogody,

• zbiór C kategorii pojęcia ocena-pogody, C = {0, 1},

• pojęcie ocena-pogody : X  C ,

• zbiór hipotez H równy zbiorowi funkcji h : X  C definiowalnych

przez pewne drzewo decyzyjne dla przyjętego zbioru dostępnych

testów,

• błąd hipotezy h względem pojęcia ocena-pogody

Formalne definicje

Formalne definicje testu, zbioru

treningowego, entropii testu względem

zbioru treningowego podane są w

Ocenianie błędu klasyfikatora – walidacja krzyżowa

T – pewien zbiór treningowy dla pojęcia c

T’  T - pewna część zbioru treningowego

h – klasyfikator obliczony ze zbioru treningowego T’

Szacunkowy błąd klasyfikacji:

zliczona liczba błędnych klasyfikacji na elementach x z T – T’

liczność zbioru T – T’

1. Należy założyć, że struktura ukryta w zbiorze treningowym T dla pojęcia c dobrze przybliża

strukturę ukrytą w całej przestrzeni X i w pojęciu c. Innymi słowy, zbiór T ma być w

stosownym sensie reprezentatywny dla przestrzeni X i pojęcia c.

2. Zbiór T’ wybrany do walidacji krzyżowej powinien być reprezentatywny dla zbioru T –

struktura ukryta w T’ powinna dobrze przybliżać strukturę ukrytą w T.

Nadmierne dopasowanie

Rozważmy pojęcie c : N  N  {0, 1}

 1 gdy k=2n lub k=2n+1

c(n,k) = 

Zbiór treningowy T dla pojęcia c dla zilustrowania nadmiernego dopasowania

x n k klasyfikacja 1 4 8 1 2 6 12 1 3 3 15 0 4 6 13 1 5 2 4 1 6 10 20 1 7 3 15 0 8 8 16 1 9 5 7 0 10 12 24 1 11 13 1 0 12 22 44 1 13 16 32 1 14 14 28 1 15 5 9 0 16 30 60 1 17 9 7 0 18 7 13 0 19 11 15 0

Dostępne testy

 Tak gdy n, k są parzyste

t

1

(n,k) = 

 Nie w przeciwnym przypadku.

 Tak gdy n jest parzysta i k=2n lub n jest nieparzysta

t

2

(n,k) = 

 Nie w przeciwnym przypadku.

 Tak gdy n jest nieparzysta i k=2n+1 lub n jest parzysta

t

3

(n,k) = 

 Nie w przeciwnym przypadku.

Dwa klasyfikatory

D1:

t

1 1 Tak 0 Nie

t

₂

t

₁

t

₃ 1 1 0 0

D2:

Tak Tak Tak Nie Nie Nie

Propozycja przeprowadzenia prostych badań

1.

Ściągnij z

http://archive.ics.uci.edu/ml/

pliki z oferowanymi tam

zbiorami treningowymi. Użyj także przekazanych przez nas plików

heart_disease.txt, iris.txt, diabets.txt, wine.txt.

2.

Dla każdego z badanych plików napisz program, który

2.1. wczyta zbiór treningowy z pliku

2.2. wśród zadeklarowanych funkcji programu będą funkcje reprezentujące

zbiór S dostępnych testów na danych, stosownie do specyfiki

konkretnego zbioru treningowego

2.3. program obliczy drzewo decyzyjne z kryterium wyboru testu przez

entropię i drzewo decyzyjne z kryterium losowego wyboru testu,

2.4. zgodnie z metodą walidacji krzyżowej zostaną obliczone

prawdopodobieństwa błędnej klasyfikacji dla jednego i drugiego drzewa

i te prawdopodobieństwa zostaną wyświetlone jako wyniki obliczeń.

Niektóre pola zastosowań metod

eksploracji danych

 Automatyczna klasyfikacja plam słonecznych

 Wsparcie diagnostyki w medycynie

 Bankowość i marketing

 Klasyfikacja danych biologicznych

.

.