Zastosowania całek oznaczonych w fizyce

(1)

Całka oznaczona funkcji

jednej zmiennej rzeczywistej

Autorzy:

Witold Majdak

(2)

Spis treści

Definicja całki oznaczonej Riemanna Własności całki Riemanna

Twierdzenie o średniej całkowej funkcji

Pierwsze zasadnicze twierdzenie rachunku całki oznaczonej Riemanna - twierdzenie o funkcji górnej granicy całkowania Drugie zasadnicze twierdzenie rachunku całki oznaczonej Riemanna - twierdzenie Newtona-Leibniza

Całkowanie przez części całek oznaczonych Całkowanie przez podstawianie całek oznaczonych Całki niewłaściwe

Kryteria zbieżności całek niewłaściwych Obliczanie pól figur płaskich

Obliczanie długości łuku krzywych Obliczanie objętości brył obrotowych Obliczanie pól powierzchni obrotowych Zastosowania całek oznaczonych w fizyce

(3)

Definicja całki oznaczonej Riemanna

Niech będzie funkcją ograniczoną. Dla każdej liczby naturalnej wybierzmy pewne elementy należące

do przedziału , które spełniają następujące zależności:

Zbiór nazywamy -tym podziałem-tym podziałem przedziału odpowiadającym ustalonej liczbie . Dla -tego

podziału przedziału oznaczmy przez długość dowolnego podprzedziału , tzn.

gdzie . Liczbę nazywamy średnicą podprzedziału . Niech będzie największą ze średnic

wszystkich podprzedziałów występujących w -tym podziale przedziału , czyli

Następnie dla każdego wybierzmy pewien element zwany punktem pośrednimpunktem pośrednim podziału .

DEFINICJA

Definicja 1: n-ta suma całkowa Riemanna

Niech

Powyższą sumę nazywamy -tą sumą całkową Riemanna-tą sumą całkową Riemanna funkcji w przedziale .

DEFINICJA

Definicja 2: Normalny ciąg podziałów przedziału

Mówimy, że ciąg podziałów przedziału jest normalnynormalny, jeżeli .

Oznacza to de facto, że gdy rośnie, to uzyskane podprzedziały (czyli części, na które dzielimy przedział ) są coraz mniejsze.

f : [a, b] → R

n

x

0

, …,

x

n

[a, b]

a =

x

0

<

x

1

< … <

x

n

= b.

= { , , …, }

Δ

n

x

0

x

1

x

n

[a, b]

n

[a, b]

Δx

k

[

x

k−1

, ]

x

k

Δ =

x

k

x

k

−

x

k−1

,

k ∈ {1, 2, …, n}

Δx

k

[

x

k−1

, ]

x

k

δ

n

[

x

k−1

, ]

x

k

n

[a, b]

= max{Δ : k = 1, 2, …, n}.

δ

n

x

k

k ∈ {1, 2, …, n}

ξ

k

∈ [

x

k−1

, ]

x

k

Δ

n

=

f( )Δ .

S

n

∑

k=1 n

ξ

k

x

k

S

n

f

[a, b]

(Δ

n

)

∞n=1

[a, b]

_n→∞

lim

δ

n

= 0

n

[a, b]

(4)

Rysunek 1: Interpretacja geometryczna przykładowej -tej sumy całkowej Riemanna dla

Rysunek 2: Interpretacja geometryczna przykładowej -tej sumy całkowej Riemanna

Przejdźmy do definicji całki oznaczonej Riemanna funkcji ograniczonej.

DEFINICJA

Definicja 3: Całka oznaczona Riemanna

Jeżeli dla każdego normalnego ciągu podziałów przedziału ciąg -tych sum całkowych Riemanna

jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów pośrednich ( ), to granicę tę nazywamy całką oznaczoną Riemannacałką oznaczoną Riemanna funkcji na przedziale i oznaczamy symbolem , tzn.

Rysunek 3: Interpretacja geometryczna całki oznaczonej Riemanna funkcji

W powyższej całce liczbę nazywamy dolną granicą całkowaniadolną granicą całkowania, liczbę górną granicą całkowaniagórną granicą całkowania, natomiast funkcjąfunkcją podcałkową

podcałkową. Jeżeli i są takimi liczbami rzeczywistymi, że , to przyjmujemy, że

Ponadto dla liczby rzeczywistej przyjmujemy, że

n n = 4 n

(Δ

n

)

∞n=1

[a, b]

(S

n

)

∞n=1

n

ξ

k

k = 1, …, n

f

[a, b]

∫

b

f(x)dx

a

I = f(x)dx :=

∫

.

a b

lim

n→∞

S

n f

a

b

f

a b

a < b

f(x)dx := − f(x)dx.

∫

b a

∫

a b

a

f(x)dx := 0.

∫

a a

(5)

Przyjrzyjmy się, w jaki sposób można obliczyć całkę oznaczoną Riemanna korzystając z jej definicji.

PRZYKŁAD

Przykład 1:

Obliczmy całkę oznaczoną funkcji stałej przyjmującej wartość na przedziale . Funkcja jest ograniczona.

Rozważając dowolny ciąg podziałów normalnych odcinka niezależnie od wyboru punktów pośrednich

otrzymujemy

Wykażemy teraz, że nie każda funkcja ograniczona jest całkowalna.

PRZYKŁAD

Przykład 2:

Zdefiniujmy tzw. funkcję Dirichletafunkcję Dirichleta za pomocą następującego przepisu:

gdzie jest zbiorem liczb wymiernych.

Funkcja jest ograniczona. Rozważmy dowolny przedział zawarty w . Dla każdej liczby naturalnej

wybierzmy dowolny podział odcinka tak, aby ciąg był normalnym ciągiem podziałów tego odcinka.

Następnie wybierzmy ciąg punktów pośrednich tego podziału, które należą do zbioru liczb wymiernych, i

utwórzmy -tą sumę całkową Riemanna . Okazuje się, że skoro dla wszystkich liczb wymiernych funkcja przyjmuje stale wartość 1, to

Podobnie, wybierzmy ciąg punktów pośrednich ustalonego podziału w taki sposób, aby należały one do zbioru liczb niewymiernych, oraz utwórzmy -tą sumę całkową Riemanna . Wiadomo, że dla dowolnej liczby niewymiernej funkcja przyjmuje wartość 0, zatem

Granice obu ciągów -tych sum całkowych Riemanna są różne, a więc całka nie istnieje.

f

c ∈ R

[a, b]

f

(Δ

n

)

∞n=1

[a, b]

ξ

k

cdx =

cΔ = c

Δ = c

[( − ) + … + ( −

)] = c

(b − a) = c(b − a).

∫

a b

lim

n→∞_k=1

∑

n

x

k _n→∞

lim

∑

k=1 n

x

k _n→∞

lim

x

1

x

0

x

n

x

n−1 _n→∞

lim

f(x) = { 1,

_0,

gdy x ∈ Q,

_{gdy x ∈ R ∖ Q,}

(Q)

(f)

[a, b]

(R)

(n)

( )

Δ

n

[a, b]

(

Δ

n

)

∞n=1

)

((

ξ

k

)

nk=1

)

(n)

( )

S

n

(f)

=

f( )Δ =

1 ⋅ Δ = 1.

S

n

∑

k=1 n

ξ

k

x

k

∑

k=1 n

x

k

(

˜)

ξ

k nk=1

)

(n)

( )

S

˜

n

(f)

=

f( )Δ =

0 ⋅ Δ = 0.

S

˜

n

∑

k=1 n

ξ

k

˜ x

k

∑

k=1 n

x

k

(n)

( f(x)dx)

∫

b a

(6)

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: Warunek wystarczający całkowalności

Warunek wystarczający całkowalności

Jeżeli funkcja jest ciągła, to jest ona całkowalna w przedziale .

PRZYKŁAD

Przykład 3:

Obliczmy całkę oznaczoną , korzystając z jej definicji. Funkcja podcałkowa jest oczywiście ciągła,

zatem na mocy twierdzenia Warunek wystarczający całkowalności całka ta istnieje. Wobec tego przy dowolnym wyborze

ciągu podziałów normalnych odcinka oraz układu punktów pośrednich ciąg -tych sum całkowych Riemanna

jest zawsze zbieżny do tej samej granicy. Możemy więc wybrać jeden szczególny ciąg podziałów normalnych

odcinka oraz układy punktów pośrednich w taki sposób, aby wygodnie było obliczyć granicę .

Otóż dla ustalonego wybierzmy punkty podziału oraz punkty pośrednie

. Wówczas każdy z odcinków ma tę samą długość . Oznacza to, że

a w rezultacie . Uwzględniając to, że

możemy wykonać następujące obliczenia:

mając na uwadze, że jest sumą kolejnych liczb .

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: o całkowalności funkcji mającej skończoną liczbę punktów

o całkowalności funkcji mającej skończoną liczbę punktów

nieciągłości

Jeżeli funkcja ma skończoną liczbę punktów nieciągłości w przedziale , to jest ona całkowalna w tym

przedziale.

Własności całki Riemanna

Przedstawimy teraz kilka podstawowych własności całki oznaczonej wynikających bezpośrednio z jej definicji.

f : [a, b] → R

[a, b]

( xdx)

∫

₁3

(f(x) = x)

[1, 3]

(n)

(

S

n

)

∞n=1

)

(

Δ

n

)

∞n=1

)

[1, 3]

(

_n→∞

lim

S

n

)

(n)

( = 1 + k)(k = 0, …, n)

x

k _n2

(x = )(k = 1, …, n)

i

k

x

k

[

x

k−1

, ]

x

k

(Δ = )

x

k n2

= max{Δ : k = 1, 2, …, n} = ,

δ

n

x

k _n2

(

lim

= 0)

n→∞

δ

n

=

f( )Δ =

(1 + k) ,

S

n

∑

k=1 n

ξ

k

x

k

∑

k=1 n ₂ n 2n

xdx

∫

1 3

=

lim

=

(1 + k) =

( +

k)

n→∞

S

n n→∞

lim

∑

_k=1 n

₂

n

2

n→∞

lim

∑

_k=1 n

₂

n

4

2

=

lim

(

1 +

k) =

(2 + 2

) = 4,

n→∞

2 n

∑

_k=1 n

₄

n

2

∑

k=1 n

lim

n→∞

1 + n

n

(n+1)n 2

1, …, n

f : [a, b] → R

[a, b]

(7)

TWIERDZENIE

Twierdzenie 3:

Twierdzenie 3: o całkowalności funkcji ciągłej w podprzedziale jej przedziału

o całkowalności funkcji ciągłej w podprzedziale jej przedziału

określoności

Funkcja całkowalna jest całkowalna w każdym podprzedziale przedziału .

TWIERDZENIE

Twierdzenie 4:

Twierdzenie 4: o całkowalności funkcji wartości bezwzględnej

o całkowalności funkcji wartości bezwzględnej

Jeżeli funkcja jest całkowalna, to całkowalna jest również funkcja

TWIERDZENIE

Twierdzenie 5:

Twierdzenie 5: o podstawowych działaniach na funkcjach całkowalnych

o podstawowych działaniach na funkcjach całkowalnych

Jeżeli funkcje oraz są całkowalne, natomiast jest liczbą rzeczywistą, to funkcje:

są również całkowalne w przedziale .

TWIERDZENIE

Twierdzenie 6:

Twierdzenie 6: o wyrażeniu całki w postaci sumy całek

o wyrażeniu całki w postaci sumy całek

Jeżeli jest funkcją całkowalną oraz , to zachodzi równość

f : [a, b] → R

[α, β]

[a, b]

f : [a, b] → R

|f| : [a, b] ∋ x ↦ |f(x)| ∈ R.

f : [a, b] → R

g : [a, b] → R

c

f + g

f − g

f ⋅ g

f

g

cf

: [a, b] ∋ x ↦ f(x) + g(x) ∈ R,

: [a, b] ∋ x ↦ f(x) − g(x) ∈ R,

: [a, b] ∋ x ↦ f(x)g(x) ∈ R,

: [a, b] ∋ x ↦ ( ) (x) ∈ R (o ile g(x) ≠ 0 dla x ∈ [a, b]),

f

_g

: [a, b] ∋ x ↦ cf(x) ∈ R

[a, b]

f : [a, b] → R

c ∈ (a, b)

f(x)dx = f(x)dx + f(x)dx.

∫

a b

∫

a c

∫

c b

(8)

Rysunek 4:

TWIERDZENIE

Twierdzenie 7:

Twierdzenie 7: o nierówności całek

o nierówności całek

Jeżeli funkcje oraz są całkowalne, a ponadto dla każdego ,

to

a

_b

Rysunek 5:

Dzięki temu rezultatowi, w pewnych szczególnych sytuacjach jesteśmy w stanie porównać wartości rozpatrywanych całek, nawet jeżeli bezpośrednie wyliczenie całek jest trudne lub wręcz niemożliwe.

= f(x)dx, = f(x)dx I1 ∫ a c I2 ∫ c b

f : [a, b] → R

g : [a, b] → R

f(x) ≤ g(x)

x ∈ [a, b]

f(x)dx ≤ g(x)dx.

∫

a b

∫

a b = f(x)dx, = g(x)dx I1 ∫ a b I2 ∫ a b

(9)

PRZYKŁAD

Przykład 4:

Zauważmy, że

Istotnie, skoro dla każdego zachodzi nierówność , a w konsekwencji , to porównanie wartości

tych całek wynika bezpośrednio z powyższego twierdzenia.

TWIERDZENIE

Twierdzenie 8:

Twierdzenie 8: o dolnym i górnym oszacowaniu całki

o dolnym i górnym oszacowaniu całki

Jeżeli jest funkcją całkowalną oraz istnieją takie liczby rzeczywiste i , że dla każdego

, to zachodzą nierówności Rysunek 6:

dx ≤

dx.

∫

0 1

2

x3

∫

0 1

2

x2

x ∈ [0, 1]

x

3

≤

_x

2

₂

x3

_≤

2

x2

f : [a, b] → R

m M

m ≤ f(x) ≤ M

x ∈ [a, b]

m(b − a) ≤ f(x)dx ≤ M(b − a).

∫

a b I = f(x)dx∫ a b

(10)

PRZYKŁAD

Przykład 5:

Oszacujmy wartość całki . Obliczenie tej całki nie byłoby łatwym zadaniem. Zauważmy, że dla każdego

zachodzą nierówności , a zatem . Ponieważ funkcja pierwiastkowa jest funkcją

rosnącą, to

Skoro długość przedziału całkowania wynosi 2, to na mocy powyższego twierdzenia dostajemy nastepujące oszacowanie wartości całki:

TWIERDZENIE

Twierdzenie 9:

Twierdzenie 9: o oszacowaniu wartości bezwzględnej całki

o oszacowaniu wartości bezwzględnej całki

Jeżeli jest funkcją całkowalną, to

DOWÓD DOWÓD

Zauważmy, że dla każdego . Całkując powyższe nierówności w granicach od do ,

otrzymujemy

co z własności modułu implikuje żądaną nierówność. CND.

CND.

Konsekwencją powyższego twierdzenia jest następujący wniosek.

WNIOSEK

Wniosek 1: o oszacowaniu wartości bezwzględnej całki

Jeżeli jest funkcją całkowalną oraz dla każdego ,

to zachodzi nierówność

dx

∫

₀2

_√

1 + x

− −

−−−

4

x ∈ [0, 2]

0 ≤

x

4

≤ 16

_{1 ≤}

_x

4

_{+ 1 ≤ 17}

1 ≤

_√

− −

x

−−−

4

+ 1

≤

_√

₁₇

−−

.

2 ≤

∫

dx ≤ 2

.

0 2

1 + x

4

− −

−−−

√

−−

17 f : [a, b] → R

f(x)dx ≤ |f(x)|dx.

∣

∣∫

a b

_∣

∣

∣ ∫

a b

−|f(x)| ≤ f(x) ≤ |f(x)|

x ∈ [a, b]

a

b

− |f(x)|dx ≤ f(x)dx ≤ |f(x)|dx,

∫

a b

∫

a b

∫

a b

f : [a, b] → R

|f(x)| ≤ M

x ∈ [a, b]

f(x)dx ≤ M(b − a).

∣

∣∫

a b

_∣

∣

(11)

Twierdzenie o średniej całkowej funkcji

TWIERDZENIE

Twierdzenie 10:

Twierdzenie 10: o średniej całkowej funkcji

o średniej całkowej funkcji

Jeżeli jest funkcją ciągłą, to istnieje element o tej własności, że

Liczbę nazywamy wówczas średnią całkową funkcjiśrednią całkową funkcji w przedziale .

Rysunek 7: Interpretacja geometryczna średniej całkowej funkcji

DOWÓD DOWÓD

Na wstępie zauważmy, że dzięki ciągłości funkcji na mocy twierdzenia Weierstrassa wartości

są skończone. Wtedy dla dowolnego mamy . Całkując te nierówności w granicach od do ,

otrzymujemy

a zatem po przekształceniach

Ponieważ funkcja ciągła w przedziale posiada własność Darboux, to dla każdej wartości istnieje taki argument

, że . W szczególności dla zdefiniowanego powyżej elementu można znaleźć taki argument ,

że , co oznacza, że

CND. CND.

Pierwsze zasadnicze twierdzenie rachunku całki

f : [a, b] → R

c ∈ [a, b]

f(c) =

1

f(x)dx.

b−a

∫

a b

f(c)

f

[a, b]

f

m =

min

f(x) oraz M =

f(x)

x∈[a,b] x∈[a,b]

max

x ∈ [a, b]

m ≤ f(x) ≤ M

a

b

m(b − a) = mdx ≤ f(x)dx ≤ Mdx = M(b − a),

∫

a b

∫

a b

∫

a b

m ≤

1

f(x)dx

≤ M.

b−a

∫

a b



 



y0



[a, b]

y ∈ [m, M]

x ∈ [a, b]

y = f(x)

y

0

c ∈ [a, b]

= f(c)

y

0

f(c) =

1

f(x)dx.

b−a

∫

a b

(12)

oznaczonej Riemanna - twierdzenie o funkcji górnej

granicy całkowania

TWIERDZENIE

Twierdzenie 11:

Twierdzenie 11: o funkcji górnej granicy całkowania

o funkcji górnej granicy całkowania

Niech będzie funkcją całkowalną. Zdefiniujmy funkcję za pomocą przepisu

Wówczas:

1. funkcja jest ciągła,

2. jeżeli jest funkcją ciągłą w punkcie , to funkcja jest funkcją różniczkowalną w punkcie oraz

przy czym jeżeli lub , to pochodną funkcji w punkcie rozumiemy tu jako pochodną jednostronną.

DOWÓD DOWÓD

Zauważmy, że twierdzenie o funkcji górnej granicy całkowania w oczywisty sposób jest prawdziwe dla funkcji tożsamościowo równej zero, gdyż wtedy funkcja jest również tożsamościowo równa zero. Rozpatrzmy przypadek, gdy osiąga wartość

niezerową w pewnym punkcie przedziału . Ustalmy . Wówczas dla otrzymujemy

Korzystając z nierówności dla całek, możemy oszacować od góry ostatni z wyrazów, jak następuje:

gdzie jest maksymalną wartością funkcji w przedziale Wartość ta jest osiągana na mocy twierdzenia Weierstrassa, gdyż , a w konsekwencji , jest funkcją ciągłą w domkniętym przedziale ograniczonym.

Ustalmy dowolną liczbę Przyjmując , dla każdego z dziedziny funkcji takiego, że , wnioskujemy, że

Wykazaliśmy w ten sposób, że

a więc funkcja jest ciągła w punkcie .

Przejdźmy do dowodu drugiej części twierdzenia. Rozważmy przypadek, gdy . (Jeżeli lub , to dalsza

część dowodu przebiega analogicznie.) Korzystając z definicji pochodnej oraz przepisu funkcji , otrzymujemy

Powołując się na twierdzenie , wnioskujemy, że dla każdego leżącego między a istnieje punkt taki, że

Kontynuując obliczenia, dostajemy

f : [a, b] → R

F : [a, b] → R

F(x) = f(t)dt dla x ∈ [a, b].

∫

a x

F

f

x

0

∈ [a, b]

F

x

0

( ) = f( ),

F

′

_x

₀

_x

₀

= a

x

0

x

0

= b

F

x

0

f

F

f

[a, b]

x

0

∈ [a, b]

x ∈ [a, b]

|F(x) − F( )| =

x

0

f(t)dt −

f(t)dt =

f(t)dt + f(t)dt −

f(t)dt =

f(t)dt .

∣

∣∫

a x

∫

a x0

_∣

∣

∣∫

a x0

∫

x0 x

∫

a x0

∣

∣ ∫

x0 x

∣

f(t)dt ≤ |f(t)|dt ≤ Mdt ≤ M|x − |,

∣

∣ ∫

x0 x

∣

∣ ∫

x0 x

∫

x0 x

x

0

M > 0

|f|

[a, b].

f

|f|

ε > 0.

δ =

ε M

x

F

|x − | < δ

x

0

|F(x) − F( )| ≤ M|x − | < M ⋅

x

0

x

0 Mε

< ε.

∀ε > 0 ∃δ > 0 ∀x ∈ [a, b] : |x − | < δ ⇒ |F(x) − F( )| < ε,

x

0

x

0

F

x

0

∈ (a, b)

x

0

x

0

= a

x

0

= b

F

( ) =

=

.

F

′

_x

₀

_lim

x→x0 F(x)−F( )x0 x−x0 _x→x0

lim

f(t)dt ∫ x0 x x−x0

x

0

b

c ∈ ( , x)

x

0

f(t)dt = f(c)(x − ).

∫

x0 x

x

0

=

f(c) =

f(c) = f( ).

f(c)(x− )0 0

(13)

Wykazaliśmy w ten sposób, że pochodna prawostronna funkcji w punkcie jest równa . W analogiczny sposób

wykazujemy, że pochodna lewostronna funkcji w punkcie również wynosi . To implikuje, że .

CND. CND.

PRZYKŁAD

Przykład 6:

Jeżeli

to dzięki ciągłości funkcji podcałkowej, na mocy twierdzenia o funkcji górnej granicy całkowania, otrzymujemy . Warto dodać, że w tym przypadku bezpośrednie obliczenie funkcji pierwotnej funkcji podcałkowej nie jest możliwe, gdyż nie jest funkcją elementarną.

PRZYKŁAD

Przykład 7:

Niech

Obliczmy pochodną funkcji w punkcie . Przyjmijmy, że

Jak łatwo zauważyć,

Wobec tego, na podstawie wzoru na pochodną funkcji złożonej, dostajemy

Skoro , a na mocy twierdzenia o funkcji górnej granicy całkowania zastosowanego do funkcji mamy

to

gdzie , gdyż .

Drugie zasadnicze twierdzenie rachunku całki

oznaczonej Riemanna - twierdzenie

Newtona-Leibniza

Leibniza

Podamy drugie podstawowe twierdzenie rachunku całkowego, zwane twierdzeniem Newtona-Leibniza, które pozwala powiązać

=

f(c) =

f(c) = f( ).

lim

x→x+ 0 f(c)(x− )x0 x−x0 _x→x

lim

+ 0

lim

c→x+ 0

x

0

F

x

0

f( )

x

0

F

x

0

f( )

x

0

F

′

( ) = f( )

x

0

x

0

F(x) =

∫

dt dla x > 0,

0 x

e

t2

(x) =

F

′

_e

x2

f : t → e

t2

f

F(x) = sin

∫

dt dla x > 0.

0 x2

t

√

F

x > 0

G(x) =

x

2

oraz H(x) = sin

_∫

dt.

0 x

t

√

F(x) = (H ∘ G)(x) = H(G(x)).

(x) =

(G(x)) (x).

F

′

_H

′

_G

′

(x) = 2x

G

′

_H

(x) = sin

,

H

′

_√

_x

(x) = sin

⋅ (x) = sin |x| ⋅ 2x = 2xsin x,

F

′

_√

−−

_x

2

_G

′

= |x| = x

x

2

−−

(14)

(1)

(2)

(3)

(4)

(5) całkę oznaczoną funkcji ciągłej z całką nieoznaczoną.

TWIERDZENIE

Twierdzenie 12:

Twierdzenie 12: Newtona-Leibniza

Newtona-Leibniza

Jeżeli jest funkcją ciągłą, natomiast jest jej dowolną funkcją pierwotną, to zachodzi równość

DOWÓD DOWÓD

Zdefiniujmy funkcję , dla każdego , kładąc

Skoro funkcja jest ciągła, to na mocy twierdzenia o funkcji górnej granicy całkowania funkcja jest różniczkowalna i zachodzi

równość we wszystkich punktach . Oznacza to, że jest funkcją pierwotną funkcji . Ponieważ każde

dwie funkcje pierwotne danej funkcji różnią się o stałą, to dla pewnej liczby rzeczywistej oraz dowolnego zachodzi równość

Z definicji funkcji wynika, że

a skoro , to możemy kontynuować obliczenia, zapisując

gdzie ostatnia równość wynika z ( 2 ). Połączenie ( 3 ) z ( 4 ) implikuje żądany wzór i kończy dowód twierdzenia. CND.

CND.

Różnicę wartości funkcji pierwotnej na końcach przedziału występującą we wzorze ( 1 ) zapisujemy również w następujący sposób:

Całkowanie przez części całek oznaczonych

Podamy teraz niezwykle ważny wzór służący do obliczania całek oznaczonych, który uzasadnimy przy pomocy twierdzenia Newtona-Leibniza.

TWIERDZENIE

Twierdzenie 13:

Twierdzenie 13: o całkowaniu przez części całek oznaczonych

o całkowaniu przez części całek oznaczonych

Jeżeli oraz są funkcjami klasy , to zachodzi równość

f : [a, b] → R

g : [a, b] → R

f(x)dx = g(b) − g(a).

∫

a b

F

x ∈ [a, b]

F(x) = f(t)dt.

∫

a x

f

F

(x) = f(x)

F

′

_{x ∈ (a, b)}

_F

_f

C

x ∈ [a, b]

g(x) = F(x) + C.

F

f(t)dt = F(b),

∫

a b

F(a) = f(t)dt = 0

∫

a a

F(b) = F(b) − F(a) = (F(b) + C) − (F(a) + C) = g(b) − g(a),

g(x) = g(b) − g(a).

∣∣

b a

f : [a, b] → R

g : [a, b] → R

C

1

f(x) (x)dx = (f(x)g(x)) −

(x)g(x)dx.

∫

a b

g

′

∣∣

b a

∫

_a b

f

′

(15)

DOWÓD DOWÓD

Skoro , to

Stosując do funkcji podcałkowej w przedziale twierdzenie Newtona-Leibniza, otrzymujemy

co dowodzi, że zachodzi ( 5 ). CND.

CND.

Zastosujmy powyższe twierdzenie do obliczenia przykładowych całek oznaczonych.

PRZYKŁAD

Przykład 8:

PRZYKŁAD

Przykład 9:

a zatem Stąd

a po przeniesieniu całki oznaczonej z prawej na lewą stronę i po podzieleniu obu stron równości przez otrzymujemy

(fg = f + g

)

′

_g

′

_f

′

∫(f(x) (x) + (x)g(x))dx = f(x)g(x) + C.

g

′

_f

′

f + g

g

′

_f

′

_{[a, b]}

(f(x) (x) + (x)g(x))dx = f(b)g(b) − f(a)g(a),

∫

a b

g

′

_f

′

ln xdx

∫

1 e

=

∣

= xln x −

⋅ xdx

∣

u(x) = ln x

_u

_′

_{(x) =}

₁ x

(x) = 1

v

′

v(x) = x

∣

∣∣

e₁

∫

1 e

1 x

= xln x − x = e − 0 − (e − 1) = 1.

∣∣

e₁

∣∣

e₁

sin xdx

∫

0 π 2

e

x

₌

∣

_{= sin x −}

_{cos xdx}

∣

u(x) = sin x

_{(x) = cos x}

u

′

v

(x) =

′

_e

x

v(x) = e

x

∣

∣ e

x

∣∣

π2 0

∫

0 π 2

e

x

=

∣

_∣

∣

_u

_′

u(x) = cos x

_{(x) = − sin x}

v

_{v(x) = e}

′

(x) =

e

_xx

∣

_∣

∣ e

=

π2

sin − sin 0

π

2 e

0

−

⎛

cos x +

sin xdx ,

⎝

⎜

⎜e

x

∣∣

π 2 0

∫

0 π 2

e

x

⎞

⎠

⎟

sin xdx =

−

cos + cos 0 −

sin xdx.

∫

0 π 2

e

x

_e

π 2

e

π2 π₂

e

0

∫

0 π 2

e

x

sin xdx =

+ 1 −

sin xdx,

∫

0 π 2

e

x

_e

π2

∫

0 π 2

e

x

2 sin xdx = ( + 1).

∫

0 π 2

e

x 1 2

e

π 2

(16)

Całkowanie przez podstawianie całek oznaczonych

Podamy twierdzenie, które podobnie jak , stanowi bardzo użyteczne narzędzie do obliczania całek oznaczonych.

TWIERDZENIE

Twierdzenie 14:

Twierdzenie 14: o całkowaniu przez podstawianie całek oznaczonych

o całkowaniu przez podstawianie całek oznaczonych

Jeżeli jest funkcją ciągłą, natomiast jest funkcją klasy taką, że oraz

, to zachodzi równość

DOWÓD DOWÓD

Skoro funkcja jest ciągła, to posiada funkcję pierwotną , a zatem . W konsekwencji

tak więc

Zauważmy, że w powyższych obliczeniach dwukrotnie użyliśmy twierdzenie Newtona-Leibniza, za pierwszym razem stosując je do funkcji podcałkowej oraz jej funkcji pierwotnej , a dalej do funkcji podcałkowej oraz jej funkcji pierwotnej .

Ponadto przedostatnia równość została uzyskana dzięki założeniu, że i .

CND. CND.

Zastosujmy twierdzenie o całkowaniu przez podstawienie do obliczenia przykładowych całek oznaczonych.

PRZYKŁAD

Przykład 10:

Zauważmy, że dokonaliśmy tu następującej zmiany wartości granic całkowania: Tabela 1: Zmiana wartości granic całkowania, gdy

f : [a, b] → R

φ : [α, β] → [a, b]

C

1

_{φ(α) = a}

φ(β) = b

f(x)dx = f(φ(t)) (t)dt.

∫

a b

∫

α β

φ

′

f

g

f = g

′

f(φ(t)) (t) = (φ(t)) (t) = (g ∘ φ (t),

φ

′

_g

′

_φ

′

₎

′

f(φ(t)) (t)dt = (g ∘ φ (t)dt = g(φ(β)) − g(φ(α)) = g(b) − g(a) =

f(x)dx.

∫

α β

φ

′

∫

α β

)

′

_∫

b a

(g ∘ φ)

′

_{g ∘ φ}

_f

_g

φ(α) = a φ(β) = b

dx =

=

− 1.

∫

0 1 x +1 x2 √

∣

t =

x

2

+ 1

dt = 2xdx

dt = xdx

1 2

∣

12

∫

1 2 dt t √

√ ∣∣

t

2 1

√

2

(t =x2+ 1)

x

0 1

t =

x

2

+ 1

_{1 2}

(17)

PRZYKŁAD

Przykład 11:

Zauważmy, że dokonaliśmy następujących zmian wartości granic całkowania: Tabela 2: Zmiana wartości granic całkowania, gdy

oraz

Tabela 3: Zmiana wartości granic całkowania, gdy

Na podstawie twierdzenia o całkowaniu przez podstawienie możemy sformułować natępujące wnioski.

WNIOSEK

Wniosek 2: o całce z funkcji parzystej w przedziale symetrycznym względem zera

Jeżeli jest liczbą dodatnią, natomiast jest parzystą funkcją ciągłą, to

DOWÓD DOWÓD

Dokonując w pierwszej z całek występujących w powyższej sumie podstawienia i stosownej zmiany granic całkowania Tabela 4: Zmiana wartości granic całkowania, gdy

otrzymujemy

Ostatnia równość wynika z faktu, że jest funkcją parzystą oraz zamiany symbolu zmiennej całkowania z na . CND. CND.

=

= ln s

= ( ln 1 − ln ln 2) = − ln ln 2.

∫

e2 ee dx x⋅ln x⋅ln(ln x)

∣

_{dt = dx}

t = ln x

₁ x

∣

∣ ∫

2 e dt t ln t

∣

_{ds = dt}

s = ln t

₁ t

∣

∫

ln 2 1 ds s

∣∣

1 ln 2 t = ln x

x

e

2

_e

e

t = ln x 2 e

s = ln t

t

2 e

s = ln t ln 2 1

a

f : [−a, a] → R

f(x)dx = 2 f(x)dx.

∫

−a a

∫

0 a

f(x)dx = f(x)dx + f(x)dx.

∫

−a a

∫

−a 0

∫

0 a

t = −x

t = −x

x

−a 0

t = −x a 0

− f(−t)dt + f(x)dx = f(−t)dt + f(x)dx = 2 f(x)dx.

∫

a 0

∫

0 a

∫

0 a

∫

0 a

∫

0 a

f

t x

(18)

Rysunek 8:

Rozumując analogicznie jak powyżej, możemy otrzymać kolejny rezultat.

WNIOSEK

Wniosek 3: o całce z funkcji nieparzystej w przedziale symetrycznym względem

zera

Jeżeli jest liczbą dodatnią, natomiast jest nieparzystą funkcją ciągłą, to

Rysunek 9:

Powyższe wnioski mają dość duże znaczenie w praktycznych obliczeniach, gdyż niejednokrotnie prościej jest znaleźć wartość funkcji pierwotnej w zerze niż w . W szczególności powyższy wniosek pozwala natychmiast podać wartość liczbową niektórych całek bez konieczności przeprowadzania złożonych rachunków.

I = f(x)dx∫ 0 a

a

f : [−a, a] → R

f(x)dx = 0.

∫

−a a I = f(x)dx∫ 0 a

−a

(19)

PRZYKŁAD

Przykład 12:

Możemy stwierdzić, że

ponieważ całkujemy po przedziale, który jest symetryczny względem zera, a funkcja sinus jest w nim nieparzysta.

Całki niewłaściwe

Właściwości całki ze względu na przedział całkowania (całka I rodzaju)

Przypomnijmy, że pojęcie całki oznaczonej Riemanna zostało przez nas zdefiniowane dla funkcji ograniczonej, określonej na przedziale domkniętym i ograniczonym. Ze względu na praktyczne zastosowania istnieje potrzeba rozszerzenia tego pojęcia na przypadek funkcji działającej na przedziale nieograniczonym lub funkcji nieograniczonej.

Na początek zdefiniujmy całkę niewłaściwą funkcji określonej na przedziale postaci , następnie , a dalej na

całym zbiorze liczb rzeczywistych.

xdx = 0,

∫

−π 2 π 2

sin

7

[a, +∞)

(−∞, b]

(20)

DEFINICJA

Definicja 4: Całka niewłaściwa Riemanna I rodzaju w przedziale

lub

Niech będzie funkcją całkowalną w sensie Riemmana na każdym z przedziałów domkniętych , gdzie

. Całką niewłaściwą Riemanna I rodzajuCałką niewłaściwą Riemanna I rodzaju funkcji nazywamy granicę

i oznaczamy ją symbolem

.

Jeżeli powyższa granica istnieje i jest skończona, to mówimy, że całka niewłaściwa jest zbieżnazbieżna, natomiast jeżeli granica ta nie istnieje lub jest niewłaściwa, to mówimy, że całka niewłaściwa jest rozbieżnarozbieżna.

Rysunek 10: Interpretacja geometryczna całki niewłaściwej Riemanna I rodzaju w przedziale

W analogiczny sposób definuje się całkę niewłaściwą Riemanna I rodzaju funkcji określonej na przedziale , jak również pojęcia jej zbieżności i rozbieżności. Przyjmujemy wówczas, że

Rysunek 11: Interpretacja geometryczna całki niewłaściwej Riemanna I rodzaju w przedziale

[a, +∞)

(−∞, b]

f : [a, +∞) → R

[a, β]

a < β

f

f(x)dx

lim

β→+∞

∫

_a β

f(x)dx

∫

a +∞

f(x)dx

∫

_a+∞

f(x)dx

∫

+∞ a [a, +∞)

f(x)dx

∫

b −∞

f

(−∞, b]

f(x)dx :=

f(x)dx.

∫

−∞ b

lim

α→−∞

∫

_α b (−∞, b]

(21)

DEFINICJA

Definicja 5: Całka niewłaściwa Riemanna I rodzaju w zbiorze liczb rzeczywistych

Niech będzie funkcją całkowalną w sensie Riemanna w każdym przedziale domkniętym zawartym w .

Całkę niewłaściwą Riemanna I rodzaju

Całkę niewłaściwą Riemanna I rodzaju funkcji w definujemy jako

gdzie jest dowolnie wybranym punktem z . Jeżeli obie całki w powyższej sumie są zbieżne, to mówimy, że całka jest zbieżna. Gdy któraś z tych całek nie istnieje lub jest rozbieżna, to mówimy, że całka jest rozbieżna.

Należy podkreślić, że jeżeli całka jest zbieżna, to można wykazać, że jej wartość nie zależy od wyboru punktu w powyższej definicji.

PRZYKŁAD

Przykład 13:

Obliczmy całkę . Otóż

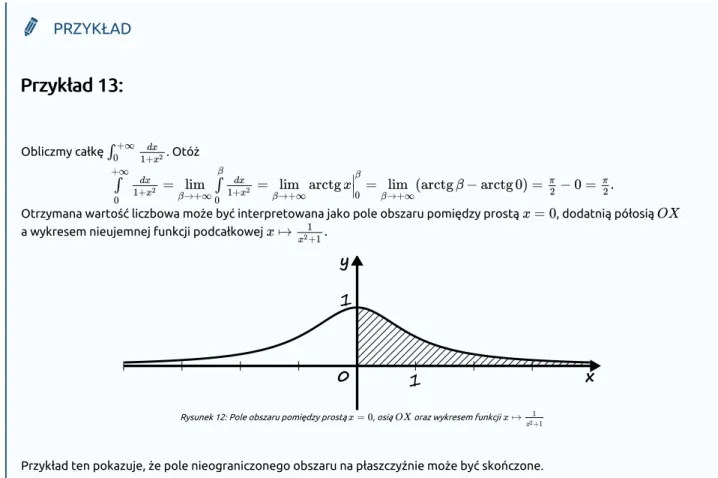
Otrzymana wartość liczbowa może być interpretowana jako pole obszaru pomiędzy prostą , dodatnią półosią a wykresem nieujemnej funkcji podcałkowej

Rysunek 12: Pole obszaru pomiędzy prostą , osią oraz wykresem funkcji

Przykład ten pokazuje, że pole nieograniczonego obszaru na płaszczyźnie może być skończone.

f : R → R

[α, β]

R

f R

f(x)dx :=

f(x)dx +

f(x)dx,

∫

−∞ +∞

∫

−∞ a

∫

a +∞

a

R

f(x)dx

∫

_−∞+∞

∫

_−∞+∞

f(x)dx

∫

_−∞+∞

a ∈ R

∫

+∞ 0 1+xdx2

=

arctg x =

(arctg β − arctg 0) = − 0 = .

∫

0 +∞ dx 1+x2

lim

β→+∞

∫

₀ β dx 1+x2

lim

β→+∞

∣∣

β 0 β→+∞

lim

π 2 π2

x = 0

OX

x ↦

1

.

+1 x2 x = 0 OX x ↦ 1 +1 x2

(22)

PRZYKŁAD

Przykład 14:

Przy ustalonej liczbie zbadajmy zbieżność całki w zależności od wartości parametru .

Przypadek 1. Przypadek 1. . Zauważmy, że a zatem Przypadek 2. Przypadek 2. .

Reasumując, całka jest zbieżna dla , a rozbieżna dla

Niewłaściwość całki ze względu na funkcję podcałkową (całka II rodzaju)

Sformułujmy teraz definicję całki niewłaściwej funkcji nieograniczonej określonej na przedziale ograniczonym.

a > 0

∫

+∞

dx

a x1p

p ∈ R

p ≠ 1

∫

a +∞

dx

x

p

=

∫

dx =

a +∞

x

−p

_lim

β→+∞

∫

a β

x

−p

_lim

β→+∞

x

−p+1

−p + 1

∣∣

β a

=

lim

=

(

−

).

β→+∞

1 (1 − p)x

p−1

∣∣

β a

1 1 − p lim

β→+∞

1 β

p−1

1 a

p−1

= {

lim

β→+∞ 1 βp−1

+∞,

0,

gdy p − 1 < 0,

gdy p − 1 > 0,

= {

∫

a +∞ dx xp

+∞,

,

1 (p−1)ap−1

gdy p < 1,

gdy p > 1.

p = 1

=

ln x =

(ln β − ln a) = +∞.

∫

a +∞ dx x _β→+∞

lim

∣∣

β a β→+∞

lim

(

∫

_a+∞ dx

)

xp

(p > 1)

(p ≤ 1).

(23)

DEFINICJA

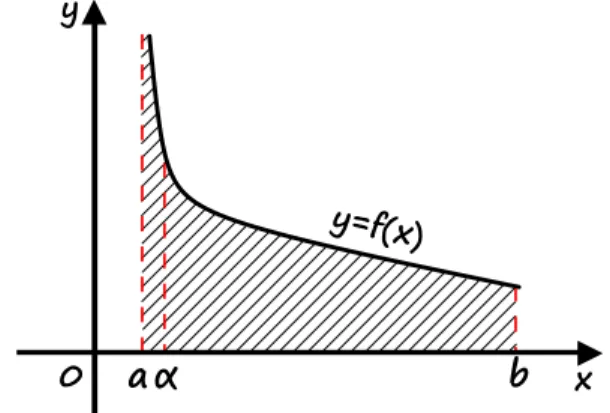
Definicja 6: Całka niewłaściwa Riemanna II rodzaju w przedziale

lub

Niech będzie funkcją całkowalną w sensie Riemmana na każdym z przedziałów domkniętych , przy

czym . Załóżmy, że funkcja jest nieograniczona w pewnym lewostronnym sąsiedztwie punktu . CałkąCałką

niewłaściwą Riemanna II rodzaju

niewłaściwą Riemanna II rodzaju funkcji nazywamy granicę

i oznaczamy ją symbolem

Jeżeli powyższa granica istnieje i jest skończona, to mówimy, że całka niewłaściwa jest zbieżnazbieżna, natomiast jeżeli granica ta nie istnieje lub jest niewłaściwa, to mówimy, że całka niewłaściwa jest rozbieżnarozbieżna.

b

Rysunek 13: Interpretacja geometryczna całki niewłaściwej Riemanna II rodzaju w przedziale

W analogiczny sposób definiujemy całkę niewłaściwą Riemanna II rodzaju w przypadku, gdy funkcja jest

całkowalna w sensie Riemmana na każdym z przedziałów domkniętych , przy czym , oraz jest nieograniczona w

prawostronnym sąsiedztwie punktu . Wówczas przyjmujemy, że

W tej sytuacji analogicznie jak wyżej definiuje się pojęcia zbieżności i rozbieżności całki niewłaściwej.

Rysunek 14: Interpretacja geometryczna całki niewłaściwej Riemanna II rodzaju w przedziale

[a, b)

(a, b]

(f : [a, b) → R)

[a, β]

(a < β < b)

(f)

(b)

(f)

f(x)dx

lim

β→b−

∫

a β

f(x)dx.

∫

a b

f(x)dx

∫

b a

f(x)dx

∫

b a [a, b)

(f : (a, b] → R)

[α, b]

(a < α < b)

(a)

f(x)dx :=

f(x)dx.

∫

a b

lim

α→a+

∫

α b (a, b]

(24)

DEFINICJA

Definicja 7: Całka niewłaściwa Riemanna II rodzaju w przedziale

Niech będzie funkcją całkowalną w sensie Riemmana na każdym z przedziałów domkniętych , przy

czym . Załóżmy, że funkcja jest nieograniczona w pewnym prawostronnym sąsiedztwie punktu

oraz

w pewnym lewostronnym sąsiedztwie punktu . Całkę niewłaściwą Riemanna II rodzajuCałkę niewłaściwą Riemanna II rodzaju funkcji w definiujemy jako

gdzie jest dowolnie wybranym punktem z . Jeżeli obie całki po prawej stronie powyższej równości są zbieżne, to mówimy, że całka jest zbieżnazbieżna. Gdy któraś z tych całek nie istnieje lub jest rozbieżna, to mówimy, że całka niewłaściwa jest rozbieżnarozbieżna.

PRZYKŁAD

Przykład 15:

Obliczmy całkę . Zauważmy, że , a zatem funkcja podcałkowa jest nieograniczona

w lewostronnym sąsiedztwie punktu . Na początku znajdźmy następującą całkę nieoznaczoną:

Otrzymujemy zatem

a więc rozpatrywana całka niewłaściwa jest rozbieżna.

Obliczmy teraz całkę podobną do tej z przykładu 2, w którym przedział całkowania był nieograniczony. Po wykonaniu poniższych obliczeń warto porównać wyniki uzyskane w obu przykładach.

(a, b)

(f : (a, b) → R)

[α, β]

(a < α < β < b)

(f)

(a)

(b)

(f) (a, b)

f(x)dx = f(x)dx + f(x)dx,

∫

a b

∫

a c

∫

c b

(c)

((a, b))

( f(x)dx)

∫

b a

( f(x)dx)

∫

b a

(

∫

1

)

0 _(x−1)dx2

(

_x→1

lim

−_(x−1)1 2

= +∞)

(1)

∫

dx

=

= ∫ dt = − + C = −

+ C.

(x−1)2

∣

∣∣

t = x − 1

dt = dx

∣

∣∣

t12 1_t _x−11

=

( −

) =

(

− 1) = +∞,

∫

0 1 dx (x−1)2 _β→1

lim

−

∫

0 β dx (x−1)2 _β→1

lim

− x−11

∣∣

β 0 β→1

lim

− β−1−1

(25)

PRZYKŁAD

Przykład 16:

Przy ustalonej liczbie zbadajmy zbieżność całki w zależności od wartości parametru

Przypadek 1. Przypadek 1. . Zauważmy, że a zatem Przypadek 2. Przypadek 2. .

Reasumując, całka jest zbieżna dla , a rozbieżna dla .

Kryteria zbieżności całek niewłaściwych

Przedstawimy kryteria zbieżności całek niewłaściwych.

TWIERDZENIE

Twierdzenie 15:

Twierdzenie 15: Kryterium porównawcze I

Kryterium porównawcze I

Niech oraz będą funkcjami ciągłymi. Załóżmy, że dla każdego .

Wówczas:

1) jeżeli całka jest zbieżna, to całka jest również zbieżna,

2) jeżeli całka jest rozbieżna, to całka jest również rozbieżna.

(b > 0)

(

∫

b

dx)

0 x1p

(p ∈ R).

p ≠ 1

∫

0 b

dx

x

p

=

∫

dx =

0 b

x

−p

_lim

α→0+

∫

b α

x

−p

_lim

α→0+

x

−p+1

−p + 1

∣∣

b α

=

lim

=

(

−

).

α→0+

1 (1 − p)x

p−1

∣∣

b α

1 1 − p lim

α→0+

1 b

p−1

1 α

p−1

= {

lim

α→0+ 1 αp−1

0,

_+∞,

gdy p − 1 < 0,

_{gdy p − 1 > 0,}

= {

∫

0 b dx xp

,

b1−p p−1

+∞,

gdy p < 1,

gdy p > 1.

p = 1

=

ln x =

(ln b − ln α) = +∞.

∫

0 b dx x _α→0

lim

+

∫

α b dx x _α→0

lim

+

∣∣

b α α→0

lim

+

(

∫

b

)

0 dxxp

(p < 1)

(p ≥ 1)

f : [a, b) → R

g : [a, b) → R

0 ≤ f(x) ≤ g(x)

x ∈ [a, b)

g(x)dx

∫

a b

f(x)dx

∫

a b

f(x)dx

∫

a b

g(x)dx

∫

a b

(26)

Przyjrzyjmy się przykładowym zastosowaniom tego kryterium, w którym dopuszczamy również możliwość, że .

PRZYKŁAD

Przykład 17:

Zbadajmy zbieżność całki . Zauważmy, że

Ponieważ dla każdego to

Stąd na mocy kryterium porównawczego I wnioskujemy rozbieżność wyjściowej całki.

PRZYKŁAD

Przykład 18:

Zbadajmy zbieżność całki . Ponieważ funkcja arcus tangens jest ograniczona od góry przez , to dla każdego

zachodzi szacowanie

Na mocy powyższego twierdzenia i zbieżności całki niewłaściwej wnioskujemy, że wyjściowa całka jest zbieżna.

TWIERDZENIE

Twierdzenie 16:

Twierdzenie 16: Kryterium porównawcze II

Kryterium porównawcze II

Niech oraz będą funkcjami ciągłymi. Załóżmy, że oraz dla każdego

oraz istnieje granica

Wówczas:

1. ze zbieżności całki dla wynika zbieżność całki ,

1. z rozbieżności całki dla wynika rozbieżność całki .

Zauważmy, że dla całki oraz są jednocześnie zbieżne bądź rozbieżne.

b = +∞

dx

∫

_e+∞2 _{x ln(ln x)}1

dx =

dx.

∫

e2 +∞ 1 x ln(ln x)

∫

₂ +∞ 1 ln x

0 ≤ ln x ≤ x − 1

x ≥ 1,

dx ≥

dx =

ln(x − 1) = +∞.

∫

2 +∞ ₁ ln x

∫

₂ +∞ ₁ x−1 _β→+∞

lim

∫

2 β 1 x−1 _β→+∞

lim

∣∣

β2

dx

∫

₁+∞ arctg x_x3₊₁ π₂

x ∈ [1, +∞)

0 ≤

arctg x_x3₊₁

≤

_2xπ3

.

dx

π 2

∫

1+∞x13

f : [a, b) → R

g : [a, b) → R

f(x) ≥ 0

g(x) > 0

x ∈ [a, b)

= K (0 ≤ K ≤ +∞).

lim

x→b− f(x) g(x)

g(x)dx

∫

a b

K < +∞

∫

f(x)dx

a b

g(x)dx

∫

a b

K > 0

∫

f(x)dx

a b

K ∈ (0, +∞)

∫

b

f(x)dx

a

∫

ab

g(x)dx

(27)

PRZYKŁAD

Przykład 19:

Zbadać zbieżność całki Niech oraz Wówczas

Ponieważ

to kryterium porównawcze II implikuje zbieżność wyjściowej całki.

W kryterium porównawczym II, podobnie jak w kryterium porównawczym I, dopuszczamy możliwość, że .

PRZYKŁAD

Przykład 20:

Zbadać zbieżność całki Niech Wtedy

Całka jest rozbieżna, więc na mocy kryterium porównawczego II rozbieżna jest też wyjściowa całka.

Powyższe kryteria zbieżności całek niewłaściwych można analogicznie sformułować dla funkcji ciągłych oraz

, które są nieograniczone w prawostronnym sąsiedztwie punktu . Warto dodać, że dopuszczamy tu możliwość, że .

PRZYKŁAD

Przykład 21:

Zbadajmy zbieżność całki . Powołajmy się na następującą nierówność dla . Stąd dla każdego

zachodzi szacowanie

Całka niewłaściwa jest zbieżna. Wobec tego kryterium porównawcze I implikuje zbieżność

wyjściowej całki.

.

∫

₀1 dx 1−x4 √4

f(x) =

_√4_1−x1 4

g(x) =

_√4_1−x1

.

=

∈ (0, +∞).

lim

x→1− 1 1−x4 √4 1 1−x √ 4 x→1

lim

− 1 (1−x)(1+x+ + )x2 x3 √ 4 1 1−x √ 4 x→1

lim

− 1 1+x+ +x2 _x3 √4 _√41₄

=

(− (1 − x ) = ,

∫

0 1 dx 1−x √4

lim

β→1−

∫

0 β dx 1−x √4

lim

β→1− 43

)

3 4

∣

∣∣

β 0 4 3

b = +∞

dx.

∫

+∞ 0 1+xx x√2

f(x) =

_1+xx x√2

,

g(x) =

_√_1+x1

.

=

= 1 ∈ (0, +∞).

lim

x→+∞ x x√ 1+x2 1 1+x √

lim

x→+∞ +1 1 x √ +1 1 x2

dx

∫

+∞ 0 √1+x1

f : (a, b] → R

g : (a, b] → R

a

a = −∞

sin

dx

∫

₀1 1 x √

sin t ≤ t

t > 0

x ∈ (0, 1]

sin

1

≤

.

x √ √1x

dx =

dx

∫

1 0 √1x

∫

01

x

− 1 2

(28)

PRZYKŁAD

Przykład 22:

Zbadajmy zbieżność całki . W tym celu zauważmy, że

a ponieważ jest całką zbieżną, to na mocy kryterium porównawczego II zbieżna jest również

wyjściowa całka.

Obliczanie pól figur płaskich

Z definicji całki oznaczonej Riemanna wynika, że jeżeli jest funkcją ciągłą i nieujemną w przedziale , to całka jest równa polu figury ograniczonej przez wykres funkcji , oś oraz proste i . Tak zadaną figurę, którą możemy opisać jako zbiór

nazywamy trapezem krzywoliniowymtrapezem krzywoliniowym. Jeżeli dla , to W rezultacie dla dowolnej funkcji

ciągłej prawdziwy jest następujący związek:

Rysunek 15: Pole figury płaskiej zwanej trapezem krzywoliniowym

∫

₀1 dx + x √ √3x

=

= 1,

lim

x→0+ 1 + x √ √3x 1 x √ 3 x→0

lim

+ x √3 + x √ √3x

lim

x→0+ 1 +1 x √ x √ 3

lim

x→0+ 1 +1 x16

dx =

dx

∫

₀1 1 x √3

∫

₀1

x

− 1 3

f : [a, b] → R

[a, b]

f(x)dx

∫

b a

P

f

OX

x = a x = b

{(x, y) ∈

R

2

: 0 ≤ y ≤ f(x), a ≤ x ≤ b},

f(x) ≤ 0

x ∈ [a, b]

P = −

∫

b

f(x)dx.

a

f : [a, b] → R

P = |f(x)|dx.

∫

a b P

(29)

PRZYKŁAD

Przykład 23:

Obliczmy pole obszaru zawartego pomiędzy wykresami funkcji , , gdzie

oraz osią . Zauważmy, że rozpatrywana figura jest sumą dwóch trapezów krzywoliniowych i :

więc jej pole jest równe sumie pól tych trapezów. Korzystając z interpretacji geometrycznej całki oznaczonej, otrzymujemy

Szukane pole wynosi zatem

Rysunek 16: ,

PRZYKŁAD

Przykład 24:

Obliczmy pole obszaru ograniczonego przez elipsę o półosiach i ( ) daną równaniem

P

f(x) = x + 1

√

− −

−−−

g(x) = (x − 1)

2

_{x ∈ [−1, 1],}

OX

T

1

T

2

= {(x, y) ∈

: 0 ≤ y ≤

, x ∈ [−1, 0]},

= {(x, y) ∈

: 0 ≤ y ≤ (x − 1 , x ∈ [0, 1]},

T

1

R

2

√

− −

x + 1

−−−

T

2

R

2

)

2

P

T1

+

P

T2

P

T1

P

T2

=

∫

dx = (x + 1

= ,

−1 0

x + 1

− −

−−−

√

2 ₃

)

32

∣∣

0 −1

2

3 = (x − 1 dx = (x − 1

∫

= .

0 1

)

2

1

3 )

3

∣∣

1 0

1

3 P = + = 1.

2 3 13 = f(x)dx PT1 ∫ −1 0 = g(x)dx PT2 ∫ 0 1

a b a, b > 0

+

= 1.

x2 a2 y 2 b2

(30)

Rysunek 17: Obszar ograniczony przez elipsę

Na początku zauważmy, że rozważany obszar jest symetryczny względem osi układu współrzędnych, a więc możemy go podzielić na cztery obszary o identycznych polach. Pole części leżącej w pierwszej ćwiartce układu współrzędnych zawarte jest między osiami i oraz częścią krzywej zadanej przepisem

Jest to więc pole figury będącej trapezem krzywoliniowym. Wówczas gdzie

Obliczmy tę całkę poprzez zamianę zmiennych w całce oznaczonej. Niech więc

Zauważmy, że , czyli zawiera się w dziedzinie funkcji cyklometrycznej arcus sinus, a więc nowa zmienna jest poprawnie określona. Ponieważ funkcja arcus sinus jest funkcją rosnącą, to jeżeli zmienia się od do , to wartości rosną od do . Mamy więc

Tabela 5: Zmiana wartości granic całkowania, gdy {OPENAGHMATHJAX (type

Wówczas

a więc

Powołując się na twierdzenie o całkowaniu przez podstawienie, otrzymujemy

Ostatecznie pole figury ograniczonej przez elipsę o półosiach i wynosi .

+ = 1 x2 a2 y2 b2

OX OY

f(x) = b

1 −

x2

, gdzie x ∈ [0, a].

a2

− −

−−−

√

P = 4 ,

P

1

= f(x)dx = b

dx.

P

1

∫

0 a

∫

0 a

1 −

x2 a2

− −

−−−

√

t = arcsin

x

dla x ∈ [0, a].

a

∈ [0, 1]

x a xa

t

x

0 a

t

0

π 2

x 0 a

t 0

π 2

x = a sin t dla t ∈ [0, ],

π 2

dx = a cos t dt.

P = 4b

∫

a cos tdt = 4ab

tdt = 4ab

(1 + cos 2t)dt

0 π 2

1 −

sin

2

t

−

−−−−−

−

√

∫

0 π 2

cos

2

_∫

0 π 2

1

2 = 2ab(t +

sin 2t

₂

) = 2ab( +

∣∣

π2

− 0) = πab.

0

π

2 sin π

2

(31)

WNIOSEK

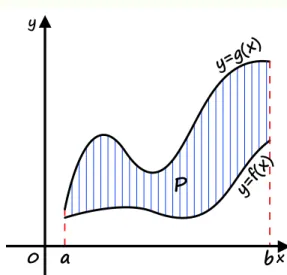
Wniosek 4: o polu figury ograniczonej przez wykresy dwóch funkcji oraz proste

pionowe

Jeżeli oraz są funkcjami ciągłymi, a ponadto dla każdego , to pole

figury ograniczonej przez wykresy tych funkcji oraz proste i wyraża się wzorem

Rysunek 18: Pole figury ograniczonej przez wykresy funkcji i oraz proste i

f : [a, b] → R

g : [a, b] → R

f(x) ≤ g(x)

x ∈ [a, b]

P

x = a x = b

P = (g(x) − f(x))dx.

∫

a b

(32)

PRZYKŁAD

Przykład 25:

Znajdźmy pole figury zawartej między wykresami funkcji i oraz prostą

Rysunek 19: Pole figury zawartej między wykresami funkcji i oraz prostą

Dla każdego zachodzi nierówność więc szukane pole obliczamy w następujący sposób:

f(x) = e

−x

_{g(x) = e}

x

_{x = 1.}

P f g x = 1

x ∈ [0, 1]

f(x) ≤ g(x),

P = ( −

∫

) dx = ( +

) = e +

− 2.

0 1

e

x

_e

−x

_e

x

_e

−x

∣∣

1 0

e

−1

(33)

PRZYKŁAD

Przykład 26:

Obliczmy pole obszaru zawartego między parabolami o równaniach

gdzie jest ustaloną liczbą dodatnią.

Rysunek 20: Pole figury zawartej między wykresami funkcji i

Rozwiązując układ równań

znajdujemy punkty przecięcia obu parabol, mające współrzędne i Zauważmy, że obszar, którego pole

chcemy obliczyć, zawarty jest między wykresami funkcji

Ponieważ dla każdego , to szukane pole wyraża się wzorem

Aby obliczyć pole figury płaskiej przy pomocy całki oznaczonej, w pewnych sytuacjach warto jest całkować względem zmiennej zamiast zmiennej . Pozwala to uniknąć dzielenia danego obszaru na mniejsze obszary oraz niepotrzebnego obliczania kilku całek.