Warunki powstania cyklu granicznego w równaniu typu Van der Pola

(1)

Warunki powstania cyklu

granicznego w równaniu

typu Van der Pola

Autorzy:

Vsevolod Vladimirov

(2)

(1) (2) (3) (4) (5) (6) (7) (8)

Warunki powstania cyklu granicznego w równaniu typu Van der Pola

Autor: Vsevolod Vladimirov

Rozpatrzmy równanie (zob. też moduł ):

Równanie to można przedstawić w postaci układu dynamicznego

Rozwiązując równanie charakterystyczne

otrzymamy:

Zatem, przy macierz linearyzaji układu ( 2 ) w punkcie stacjonarnym ma parę czysto urojonych wartości własnych .

Przeanalizujemy teraz warunki powstania cyklu granicznego w otoczeniu tego punktu, kładąc . Obliczmy w tym celu macierz

której kolumny , spełniają równanie

Równanie to jest równoważne układowi

Zapiszmy pierwszy układ w postaci

Zatem uklad ( 3 )-( 6 ) jest spełniony gdy , , przy czym , mogą być wybrane w dowolny sposób

(eliminujemy, oczywiście, przypadek ).

Przyjmując, że , otrzymujemy następujący wzór:

Mnożąc układ ( 1 ) z lewej strony przez oraz stosując zamianę zmiennych

otrzymujemy

Zatem

Wykorzystując wzór na obliczenie pierwszego indeksu Floqueta 1

+ (β − 2α)

+ v = 0.

v d2 d t2

v

2 d v_{d t}

= (

) ( ) + (

) .

( )

v

w

′

₀

−1

1 2 α

v

w

0 −β w

v

2

det (

−λ

₋₁

1 _{2 α − λ}

) =

λ

2

− 2 α λ + 1 = 0,

(α) = α ± i

= α ± i + O(| |).

λ

±

√

1 − α

− −

−−−

2

α

2

α = 0,

(0, 0)

(0) = ± i

λ

±

α = 0

P = (R, −I),

R = ( ,

R

1

R

2

)

tr

−I = −( ,

I

1

I

2

)

tr

(

0 ₋₁

1 ₀

) (R + i I) = iR − I.

(

0 ) R = −I, (

) I = R.

−1

1

0

0 −1

1

0 = − ,

R

2

I

1

= ,

R

1

I

2

=

,

I

2

R

1

− =

I

1

R

2

, .

=

R

1

I

2

R

2

= −

I

1

I

1

I

2

= = 0

I

1

I

2

= −1

I

1

I

2

= 0

P = (R, −I) = (

0 ) =

.

1

0 P

−1

= P

P

−1

v = y,

w = x

= (

) ( ) + (

) .

( )

x

y

′

₀

1 −1

0 x

y

−βxy

2

0 f(x, y) = −βx , g(x, y) = 0.

y

2

a = [

1

+

] +

(3)

gdzie otrzymujemy, że - 1.0 - 0.5 0.5 1.0 1.5 V - 1.5 - 1.0 - 0.5 0.5 1.0 W

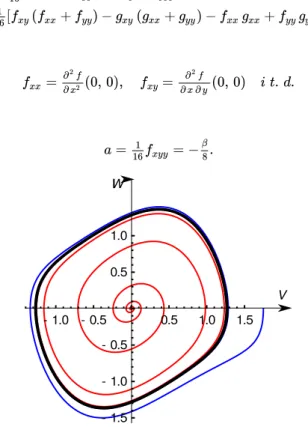
Rysunek 1: Portret fazowy układu uzyskany w eksperymentach numerycznych przy , : pogrubiona linia czarna obrazuje rozwiązanie okresowe; lina czerwona oraz niebieska opisują trajektorie nawijające się na trajektorię okresową z obszaru wewnętrznego i zewnętrznego (odpowiednio).

Z powyższego wzoru wynika, że w przypadku, gdy , układ posiada stabilne rozwiązanie okresowe przy małych . Przy oraz przy małych ujemnych wartościach w układzie realizują się niestabilne rozwiązania okresowe.

Poniżej przedstawiono implementację w pakiecie "Mathematica" symulacji numerycznej równania Van der Pola. Na Rys. 1

przedstawiony jest portret fazowy ilustrujący przebieg rozwiązań w otoczeniu stabilnej trajektorii okresowej.

Przypisy

a = [

1

+

] +

16

f

xxx

f

xyy

g

xxy

g

yyy

+ [

1

(

+

) −

(

+

) −

+

] ,

16

f

xy

f

xx

f

yy

g

xy

g

xx

g

yy

f

xx

g

xx

f

yy

g

yy

=

(0, 0),

=

(0, 0) i t. d.

f

xx ∂ f 2 ∂ x2

f

xy ∂ f 2 ∂ x ∂ y

a =

1

= − .

16

f

xyy β₈ α = 0.2 β = 1

β > 0

α > 0

β < 0

α,

Clear[α, β, z]

z = 1;

β = 1;

α = 0.2;

row1 = V [t] == z ∗ W[t];

∂

t

row2 = W[t] == −z ∗ ((βV [t] 2 − 2α)W[t] + V [t]);

∂

t ∧

warV = V [0] == 0.01; warW = W[0] == 0.0;

rozw = NDSolve[{row1, row2, warV, warW}, {V , W}, {t, 0, 100},

AccuracyGoal → 13, PrecisionGoal → 13, MaxSteps → 10 5];

∧

h30 = ParametricPlot[{Evaluate[{V [t], W[t]}/.rozw]}, {t, 0, 50},

PlotRange → Full, PlotStyle → {Red}, AxesLabel → {V , W}];

warV1 = V [0] == 1.75; warW1 = W[0] == 0.0;

rozw2 = NDSolve[{row1, row2, warV1, warW1}, {V , W}, {t, 0, 100},

AccuracyGoal → 13, PrecisionGoal → 13, MaxSteps → 10 5];

∧

h31 = ParametricPlot[{Evaluate[{V [t], W[t]}/.rozw2]}, {t, 0, 30},

PlotRange → Full, PlotStyle → {Blue}, AxesLabel → {V , W}];

warV2 = V [0] == 1.27; warW2 = W[0] == 0.0;

rozw2 = NDSolve[{row1, row2, warV2, warW2}, {V , W}, {t, 0, 100},

AccuracyGoal → 13, PrecisionGoal → 13, MaxSteps → 10 5];

∧

h32 = ParametricPlot[{Evaluate[{V [t], W[t]}/.rozw2]}, {t, 0, 20},

PlotRange → Full, PlotStyle → {Black, Thick}, AxesLabel → {V , W}];

fig2A = Show[h31, h30, h32]

(4)

1. Szczegóły wyprowadzenia tego wzoru można znaleźć w dopełnieniu do rozdziału 3.4 książki J. Guckenheimer and Ph. Holmes, Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields, Springer, NY, 1987

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 07:28:57

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=dad8fa472cb36224ae6cc33420c175b7