Płaszczyzny w trójwymiarowej przestrzeni rzeczywistej

(1)

Płaszczyzny w

trójwymiarowej przestrzeni

rzeczywistej

Autorzy:

Michał Góra

2019

(2)

(1)

(2)

(3)

Płaszczyzny w trójwymiarowej przestrzeni rzeczywistej

Autor: Michał Góra

DEFINICJA

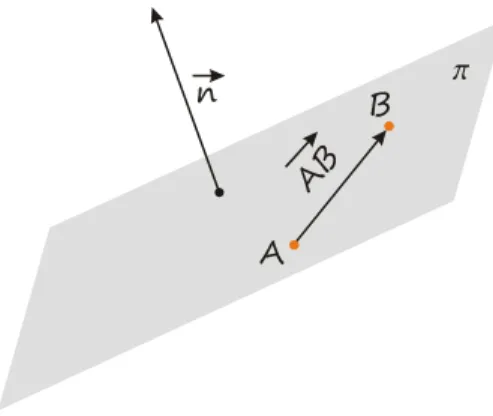
Definicja 1: Wektor normalny płaszczyzny

Wektor

Wektor jest prostopadły do płaszczyzny jest prostopadły do płaszczyzny , jeżeli dla dowolnych dwóch jej punktów i wektory oraz są prostopadłe.

Każdy niezerowy wektor prostopadły do płaszczyzny nazywamy wektorem normalnymwektorem normalnym tej płaszczyzny (zob. Rys. 1).

Rysunek 1: Płaszczyzna i jej wektor normalny.

Równanie normalne płaszczyzny

Równanie płaszczyzny przechodzącej przez punkt oraz prostopadłej do niezerowego wektora ma postać

Jest to tzw. równanie normalne płaszczyznyrównanie normalne płaszczyzny.

Równanie płaszczyzny przechodzącej przez trzy punkty

Każde trzy niewspółliniowe (nieleżące na jednej prostej) punkty , gdzie , wyznaczają dokładnie jedną płaszczyznę , która je zawiera. Równanie tej płaszczyzny ma postać:

Jest to tzw. wyznacznikowe równanie płaszczyznywyznacznikowe równanie płaszczyzny.

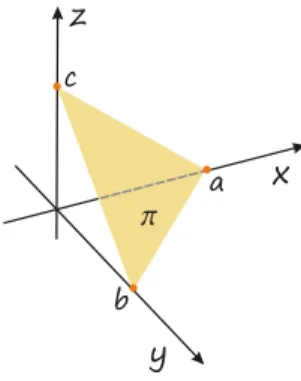
Równanie odcinkowe płaszczyzny

Równanie

w którym są liczbami różnymi od zera, nazywamy równaniem odcinkowym płaszczyzny równaniem odcinkowym płaszczyzny .

Płaszczyzna opisana równaniem ( 3 ) przecina osie oraz układu współrzędnych w punktach równych

n⃗

π

A B

−→

AB

−

n⃗

π

P ( , , )

x

0

y

0

z

0

n⃗

= (A, B, C)

π :

A (x − ) + B (y − ) + C (z − ) = 0.

x

0

y

0

z

0

( , , )

P

i

x

i

y

i

z

i

i = 1, 2, 3

π

π :

∣

= 0.

∣

x − x

1

−

x

2

x

1

−

x

3

x

1

y − y

1

−

y

2

y

1

−

y

3

y

1

z − z

1

−

z

2

z

1

−

z

3

z

1

∣

π :

x

+ + = 1,

a yb zc

a, b, c

π

Ox, Oy

Oz

Oxyz

(a, 0, 0)

x y

(0, b, 0)

z

(0, 0, c)

(3)

(4)

odpowiednio , , .

Rysunek 2: Płaszczyzna przecinająca osie układu w punktach .

Równanie parametryczne płaszczyzny

Równanie płaszczyzny przechodzącej przez punkt i równoległej do dwóch niezerowych, nierównoległych

wektorów oraz ma postać:

Jest to tzw. równanie parametryczne płaszczyznyrównanie parametryczne płaszczyzny.

(a, 0, 0)

P

x

P

y

(0, b, 0)

P

z

(0, 0, c)

(a, 0, 0), (0, b, 0), (0, 0, c) Px Py Pz

π

P ( , , )

x

0

y

0

z

0

= ( , , )

v⃗

v

x

v

y

v

z

w⃗

= ( , , )

w

x

w

y

w

z

π :

⎧

, gdzie r, s ∈ R.

⎩

⎨

⎪

x =

x

0

+ r + s

v

x

w

x

y = + r + s

y

0

v

y

w

y

z = + r + s

z

0

v

z

w

z

(4)

PRZYKŁAD

Przykład 1: Wyznaczanie równania płaszczyzny

Rozważmy trzy punkty: . Ponieważ wektory oraz

nie są równoległe (gdyż ), zatem punkty wyznaczają dokładnie jedną płaszczyznę . Wyznaczymy teraz jej równania.

Ponieważ

zatem, na podstawie wzoru ( 2 ), równanie normalne płaszczyny to

wektorem normalnym płaszczyzny jest wektor

Z postaci normalnej płaszczyzny otrzymujemy natychmiast jej postać odcinkową

Aby wyznaczyć postać parametryczną płaszczyzny wystarczy zauważyć, że wektory oraz

są wektorami do niej równoległymi. Stąd oraz ze wzoru ( 4 ) wynika, że postać parametryczna płaszczyzny to

gdzie

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 16:10:28

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=95c2905c9c9f3c3f6b6022990887cec6