Wykad 13

(1)

MECHANIKA 2

Wykład Nr 13

Dynamika ruchu płaskiego

ciała sztywnego

(2)

Ciało

sztywne

porusza

się

ruchem

postępowym,

wywołanym działaniem sił zewnętrznych:

,

,...,

.

Ruch postępowy ciała sztywnego

Ruch postępowy - wszystkie

punkty ciała przemieszczają się z prędkościami o jednakowych:

kierunkach, zwrotach i

wartościach.

1

(3)

Dynamiczne równanie ruchu postępowego

ciała sztywnego

Na podstawie twierdzenia o ruchu środka masy, dynamiczne równanie ruchu można zapisać w postaci:

gdzie: m – masa ciała sztywnego

– przyśpieszenie środka masy

(1)

C

a

ρ

W prostokątnym układzie współrzędnych

(4)

Pochodna względem czasu krętu ciała względem jego środka masy równa jest sumie geometrycznej momentów wszystkich sił zewnętrznych względem tego środka.

Twierdzenie o pochodnej krętu

(3)

Kręt ciała sztywnego względem środka masy jest równy zeru .

Z równania (3) wynika, że gdy ciało porusza się ruchem postępowym to suma geometryczna momentów sił zewnętrznych względem środka masy ciała musi być równa zeru.

0ρ ρ = c K (4) Wniosek: siły zewnętrzne muszą tworzyć układ, który ma

(5)

Ruchem płaskim ciała sztywnego nazywamy taki

ruch, w którym wszystkie punkty ciała poruszają się

po

płaszczyznach

równoległych

do

pewnej

płaszczyzny

Π

, zwanej płaszczyzną kierującą.

Ruch płaski ciała sztywnego

(6)

Przyjmijmy iż przedstawiony na rysunku przekrój ciała otrzymano w wyniku przecięcia płaszczyzny równoległej do płaszczyzny kierującej i przechodzącej przez środek masy C.

(7)

Położenie rozpatrywanego ciała sztywnego możemy określić za pomocą współrzędnych x_c, y_c środka masy C w układzie nieruchomym Oxyz i kąta obrotu α tego ciała względem układu ruchomego C x’y’z’, którego początek C jest umieszczony w środku masy.

Ruch płaski ciała sztywnego

Ruch postępowy określa ruch punktu C na płaszczyźnie xy, a ruch obrotowy odbywa się wokół osi centralnej Cz’, przechodzącej przez środek masy.

Ciało sztywne porusza się ruchem płaskim, jeżeli

obraca się wokół osi nie zmieniającej kierunku i

porusza się ruchem postępowym po płaszczyźnie

prostopadłej do osi obrotu.

Ruch swobodnego ciała sztywnego jest płaski, jeżeli chwilowe osie obrotu nie zmieniają kierunku (pozostają stale równoległe do głównej centralnej osi bezwładności tego ciała).

(8)

dynamiczne równania ruchu postępowego po płaszczyźnie x,y

zasadę krętu ruchu obrotowego

Dynamiczne równania ruchu płaskiego ciała sztywnego

Aby

otrzymać

dynamiczne

równania

ruchu

(9)

Dynamiczne równania ruchu płaskiego ciała sztywnego

(5)

c c

y

x

&

,

_{− składowe przyspieszenia środka masy C}

z

I

− moment bezwładności rozpatrywanego ciała względem osi z

ε

− przyspieszenie kątowe ciała względem osi obrotu (z) Równanie ruchu postępowego w kierunku x

Równanie ruchu postępowego w kierunku y

Zasada krętu ruchu obrotowego względem osi z

(10)

Dynamiczne równania ruchu płaskiego ciała sztywnego

Otrzymane trzy dynamiczne równania ruchu (5)

odpowiadają liczbie stopni swobody ciała

sztywnego poruszającego się ruchem płaskim.

(11)

Przypadek a) – toczenie z po

ś

lizgiem

Przykład 1. Krążkowi o masie

m i promieniu r nadano początkową prędkość kątową ω_o, a następnie postawiono go na płaszczyźnie poziomej.

Obliczyć drogę s, po przebyciu której krążek zatrzyma się, czas

t oraz funkcje: υ = f₁(t), ω =

f₂(t), mając także dane: µ −

współczynnik tarcia

ślizgowego, f – współczynnik

tarcia tocznego.

(12)

Równanie ruchu środka masy krążka w ruchu postępowym na kierunkach x i y

Równanie ruchu obrotowego wokół środka masy (5)

W przypadku tarcia z poślizgiem

(13)

Po przekształceniu otrzymujemy:

Przypadek a) – toczenie z po

ś

lizgiem

Równanie drogi środka masy:

Prędkość liniowa środka masy C:

Po wykorzystaniu warunków początkowych iiiiiiiiiiiiiiiiiiiiiii stałe całkowania C = C = 0

0 ,

0 =

=

x

t

&

(14)

Stąd

Przypadek a) – toczenie z po

ś

lizgiem

Prędkość kątowa krążka:

Równanie kąta obrotu krążka:

Po wykorzystaniu warunków początkowych stałe całkowania wynoszą: C₃ = ω_o , C₄ = 0

o

(15)

Stąd

W chwili zatrzymania się krążka iiiiiii , stąd czas t

ϕ

&= 0 ₁ wynosi:

Przypadek a) – toczenie z po

ś

lizgiem

Na tej podstawie wyznaczymy drogę s jaką przebędzie krążek do chwili zatrzymania się po czasie t :

(16)

(17)

Równania ruchu środka masy krążka w ruchu postępowym:

Równanie ruchu obrotowego krążka wokół środka masy

Przypadek b) – toczenie bez po

ś

lizgu

(18)

Przypadek b) – toczenie bez po

ś

lizgu

W rozpatrywanym przypadku toczenia krążka bez poślizgu wartość siły tarcia tocznego T₂ musi być mniejsza od wartości siły tarcia ślizgowego T₁ .

gdzie: stąd Zatem Otrzymamy równania w postaci:

(19)

Po dwukrotnym całkowaniu względem czasu otrzymamy:

Po wykorzystaniu warunków początkowych iiiiiiiiiiiiiiiiiiiiiiiiii wyznaczamy stałe całkowania C₁ = ω_or ; C₂ = 0

r x

x

t = 0, = 0, &=

ω

_o Stąd:

Przypadek b) – toczenie bez po

ś

lizgu

Prędkość kątowa krążka:

(20)

Po wykorzystaniu warunków początkowych iiiiiiiiiiiiiiiiiiiiiii stałe całkowania C₃ = ω_o, C₄ = 0.

o

t = 0,ϕ = 0,ϕ&= ω

Stąd:

W chwili zatrzymania się krążka prędkość kątowa iiiiiii, stąd czas t₂, po którym krążek się zatrzyma, wynosi:

0

=

ϕ&

Przypadek b) – toczenie bez po

ś

lizgu

(21)

Jednorodny pręt o długości l i masie m zawieszono na pionowych nitkach w punktach A i B. Znaleźć przebieg siły w funkcji czasu w nitce zaczepionej w punkcie A po zerwaniu nitki w punkcie B.

a) nitka doskonale wiotka i doskonale nieodkształcalna

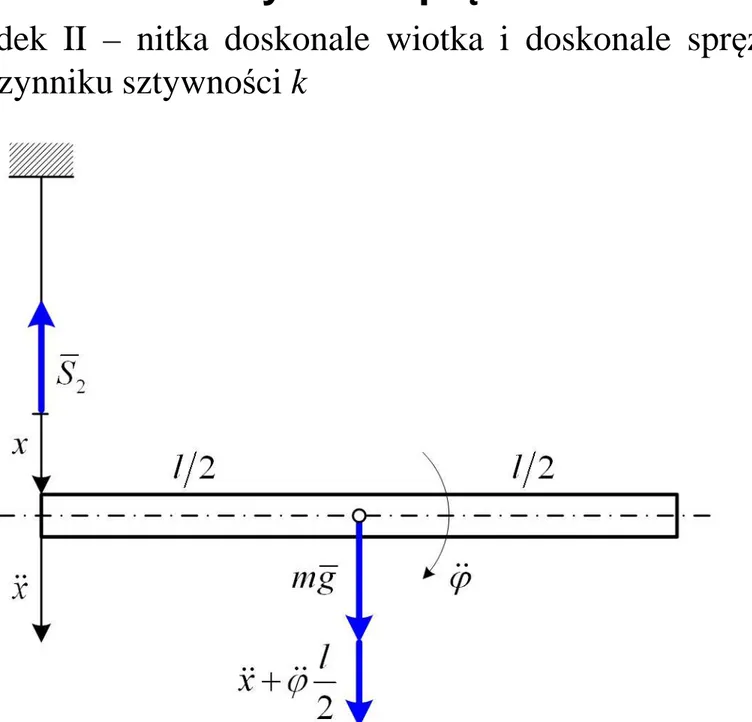
b) nitka doskonale wiotka i doskonale sprężysta o współczynniku sztywności k

Przykład 2

A B

Dane: m, l, k

(22)

Przypadek I – nitka doskonale wiotka i doskonale nieodkształcalna

Dynamiczne równania ruchu pr

ę

ta

Dynamiczne równania ruchu płaskiego pręta mają postać:

Po rozwiązaniu powyższych równań otrzymamy stałą wartość siły w nitce

(23)

Rysunek pręta

Przypadek II – nitka doskonale wiotka i doskonale sprężysta o współczynniku sztywności k

(24)

Dynamiczne równania ruchu pr

ę

ta

Po przekształceniu:

Stąd:

Dynamiczne równania ruchu mają postać:

Rozwiązanie otrzymanego równania różniczkowego jest wyrażone funkcją:

(25)

Stałe całkowanie wyznaczamy z warunków początkowych: 0 , 2 , 0 = = = = x x mg k x t _o & Stąd Po podstawieniu:

Równania ruchu pręta

Równanie ruchu pręta możemy ostatecznie zapisać:

(26)

Przykład 3

Dane: m, r,

AB = 3r, µ, f.

Szukane: a = ? M₀ = ?

Pojazd składający się z dwóch kół o jednakowej masie m i promieniu r oraz pręta o długości 3r i masie 3m, toczy się po powierzchni poziomej, dla której współczynnik tarcia ślizgowego wynosi µ, a tocznego – f. Wyznaczyć:

przyspieszenie pojazdu a;

moment silnika M₀, przy którym nastąpi poślizg tylnego koła.

(27)

Rozwi

ą

zanie

(28)

Rozwi

ą

zanie

(29)

(30)

9 równań!

a

,

M

,

N

,

N

,

T

,

T

,

R

,

R

,

R

,

R

_Ax _Ay _Bx _By ₁ ₂ ₁ ₂ ₀

10 niewiadomych:

Dodatkowo uwzględniamy warunek poślizgu:

(31)

Przykład 4

Przez krążek zawieszony na poziomej osi przerzucono nieważ-ką i nierozciągliwą nić, do końców której przymocowano ciężarki o masach m₁ i m₂. Masa krążka wy-nosi m. Wyznaczyć:

liniowe przyspieszenie ciężar-ków;

siły naciągu lin.

Pominąć tarcie cięgna o krążek. Załóżmy ponadto, że m > m .

(32)

Rozwi

ą

zanie

Dynamiczne równania ruchu (postępowego) każdego z bloczków:

(33)

Dynamiczne równanie ruchu (obrotowego) krążka:

O gdzie:

M₁ = rN₁ – moment siły N₁ względem punktu O;

M₂ = –rN₂ – moment siły N₂ względem punktu O.

ε

– przyspieszenie kątowe krążka

(34)

Ponadto mamy

Zatem:

(35)

Przykład 5

Jednorodny walec i jednorodna kula staczają się bez poślizgu z równi pochyłej o kącie nachylenia α i wysokości h. Masy i promienie obu ciał są jednakowe. Które z nich stoczy się wcześniej?

(36)

Rozwi

ą

zanie

Dynamiczne równania ruchu postępowego:

– wektorowo

Skalarnie:

Mamy:

Ponieważ nie ma poślizgu, tarcie można traktować jako statyczne:

(37)

Rozwi

ą

zanie

– wektorowo

Skalarnie:

gdzie:

Dynamiczne równania ruchu obrotowego:

ponieważ nie ma poślizgu.

(38)

Z układu dynamicznych równań obliczamy:

Uwaga!

(39)

Większe przyspieszenie liniowe ma ciało o mniejszym momencie bezwładności.

Wniosek!

Dla walca:

Dla kuli:

(40)

Suma prac sił wewnętrznych ciała sztywnego na dowolnym przesunięciu jest równa zeru, gdyż odległości między punktami tego ciała nie ulegają zmianie.

Zasada równowa

ż

no

ś

ci energii kinetycznej i pracy dla

ciała sztywnego

Stąd zasada równoważności energii kinetycznej i pracy dla ciała sztywnego przyjmuje postać:

(6)

Przyrost energii kinetycznej ciała sztywnego na pewnym

przesunięciu jest równy sumie prac sił zewnętrznych

(41)

Przykład 3:

Walec o masie m i promieniu r jest owinięty linką. Obliczyć prędkość v i siłę S po opadnięciu o wysokość h.

Dane: m, r, h

(42)

Zatem

(43)

Siłę w linie wyznaczymy z dynamicznych równań ruchu:

Po rozwiązaniu:

W kierunku osi x

Dla ruchu obrotowego

(I

_o

= mr

2

/2)

(44)

Przykład 7

Karuzela, którą można uważać za poziomy krążek o masie m₁ = 320 kg, może się obracać wokół osi pionowej. Na obwodzie karuzeli stoi człowiek o masie m₂ = 80 kg. O jaki kąt obróci się karuzela, jeśli człowiek ten poruszając się po jej obwodzie, obejdzie karuzelę dookoła, wracając do punktu wyjścia leżącego na tej karuzeli. Człowieka uznać za punkt materialny, a karuzelę – za bryłę sztywną.

Dane: m₁ = 320 kg, m₂ = 80 kg, α₂ = 2π. Szukane: α₁ = ? Wielkości pomocnicze: r – promień karuzeli; v – prędkość człowieka u – prędkość liniowa karuzeli

(45)

Rozwi

ą

zanie

Na człowieka oraz karuzelę działają siły pionowe: grawitacji i nacisku, które się równoważą. Ponadto człowiek idąc działa siłą swoich mięśni, a na karuzelę siłą tarcia. Ponieważ porusza się ruchem jednostajnym po okręgu, zatem tarcie i siła mięśni się również równoważą, a co za tym idzie, suma momentów tych sił względem punktu O jest równa zeru.

Zatem spełniona jest zasada zachowania krętu!

Kręt przed ruchem (równy zeru) jest równy sumie krętów karuzeli i człowieka.

(46)

ω₁ – prędkość kątowa karuzeli;

ω₂ – prędkość kątowa człowieka;

Człowiek względem karuzeli porusza się z prędkością kątową ω₁ + ω₂, zatem czas, po którym obejdzie karuzelę dookoła, wynosi: