Składanie funkcji

(1)

Składanie funkcji

Autorzy:

Anna Barbaszewska-Wiśniowska

(2)

Składanie funkcji

Autor: Anna Barbaszewska-Wiśniowska

DEFINICJA

Definicja 1: Złożenie funkcji

Złożeniem funkcji

Złożeniem funkcji i i , gdzie nazywamy funkcję oznaczoną , określoną następująco , , dla każdego .

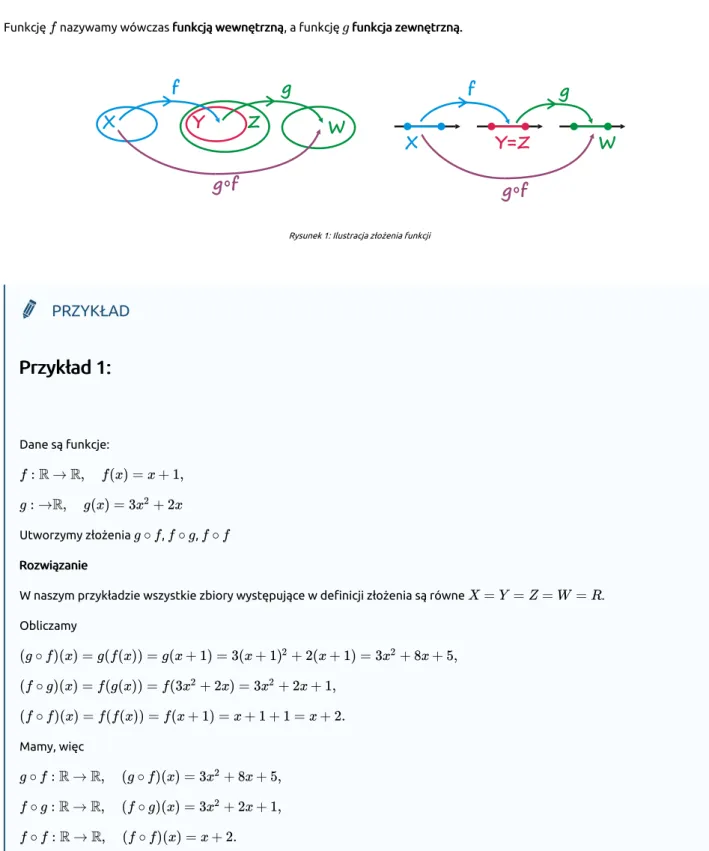
Funkcję nazywamy wówczas funkcją wewnętrznąfunkcją wewnętrzną, a funkcję funkcja zewnętrzną.funkcja zewnętrzną.

Rysunek 1: Ilustracja złożenia funkcji

PRZYKŁAD

Przykład 1:

Dane są funkcje: Utworzymy złożenia , , Rozwiązanie Rozwiązanie

W naszym przykładzie wszystkie zbiory występujące w definicji złożenia są równe . Obliczamy Mamy, więc

f : X → Y g : Z → W

Y ⊂ Z

g ∘ f

g ∘ f : X → W (g ∘ f)(x) = g(f(x))

x ∈ X

f

g

f : R → R, f(x) = x + 1,

g : →R, g(x) = 3 + 2x

x

2

g ∘ f f ∘ g f ∘ f

X = Y = Z = W = R

(g ∘ f)(x) = g(f(x)) = g(x + 1) = 3(x + 1 + 2(x + 1) = 3 + 8x + 5,

)

2

_x

2

(f ∘ g)(x) = f(g(x)) = f(3 + 2x) = 3 + 2x + 1,

x

2

_x

2

(f ∘ f)(x) = f(f(x)) = f(x + 1) = x + 1 + 1 = x + 2.

g ∘ f : R → R, (g ∘ f)(x) = 3 + 8x + 5,

x

2

f ∘ g : R → R, (f ∘ g)(x) = 3 + 2x + 1,

x

2

f ∘ f : R → R, (f ∘ f)(x) = x + 2.

(3)

UWAGA

Uwaga 1:

Jak widać z powyższego przykładu, składanie funkcji jest operacją nieprzemiennąoperacją nieprzemienną.

UWAGA

Uwaga 2: Warunek złożenia funkcji

Jeżeli funkcja oraz podane są jedynie za pomocą wzorów, to jest możliwe ich złożenie , jeśli tylko niepusty jest zbiór . Zbiór ten jest wówczas dziedziną (naturalną) złożenia.

ZADANIE

Zadanie 1:

Treść zadania: Treść zadania:

Niech , . Utworzymy złożenie , podając ich wzory i dziedziny.

Rozwiązanie: Rozwiązanie: Mamy więc Odpowiedź Odpowiedź

f

g

g ∘ f

{x ∈ R : x ∈

D

f

i f(x) ∈

D

g

}

f(x) = log x g(x) = 3x + 5

f ∘ g

(f ∘ g)(x) = f(g(x)) = f(3x + 5) = log(3x + 5),

= {x ∈ R : x ∈

i g(x) ∈

},

Df∘g

Dg

Df

= R,

= (0, +∞).

Dg

Df

x ∈ R i 3x + 5 > 0, czyli x > − .

5 3

(f ∘ g)(x) = log(3x + 5),

Df∘g

= ( , +∞).

−5 3

(4)

ZADANIE

Zadanie 2:

Rozwiązanie: Rozwiązanie: Mamy więc . Odpowiedź Odpowiedź

ZADANIE

Zadanie 3:

Rozwiązanie: Rozwiązanie:

Mamy więc i . Rozwiązując ostatnią nierówność otrzymujemy , czyli (korzystamy z faktu, że funkcja logarytmiczna jest rosnąca, gdyż tu podstawa logarytmu równa się czyli jest większa od jedynki). Odpowiedź Odpowiedź

f(x) = log x g(x) = 3x + 5

g ∘ f

(g ∘ f)(x) = g(f(x)) = g(log x) = 3 log x + 5,

= {x ∈ R : x ∈

i f(x) ∈

},

Dg∘f

Df

Dg

= (0, ∞),

= R.

Df

Dg

x > 0

(g ∘ f)(x) = 3 log x + 5,

Dg∘f

= (0, ∞)

f(x) = log x g(x) = 3x + 5

f ∘ f

(f ∘ f)(x) = f(f(x)) = f(log x) = log(log x),

= {x ∈ R : x ∈

i f(x) ∈

}.

Df∘f

Df

x > 0 log x > 0

log x > log 1

x > 1

log x = lo x

g

10

(5)

TWIERDZENIE

Twierdzenie 1: O monotoniczności złożeń

Złożenie dwóch funkcji rosnących jest funkcją rosnącą. Złożenie dwóch funkcji malejących jest funkcją rosnącą.

Złożenie funkcji rosnącej i malejącej w dowolnej kolejności jest funkcją malejącą.

PRZYKŁAD

Przykład 2:

Zbadamy monotoniczność danej funkcji i określimy rodzaj jej monotoniczności. Pokażemy, że funkcja jest funkcją rosnącą.

Rozwiązanie Rozwiązanie

Funkcję potraktujemy jako funkcję złożoną z trzech funkcji . Kładziemy:

, ,

Sprawdzimy, czy dobrze określiliśmy funkcje składowe.

Z łatwością określamy monotoniczność funkcji składowych. Funkcja jest funkcją malejącą, jest funkcją rosnącą, zatem ich złożenie jest funkcją malejącą. Funkcja jest funkcją malejącą jako funkcja wykładnicza o podstawie z

przedziału więc jej złożenie z funkcją malejącą jest funkcją rosnącą. A to złożenie jest badaną funkcją .

Odpowiedź Odpowiedź

Funkcja jest rosnąca.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

f

1

(x) = 2

f

2

f

1

f

3

(0, 1)

f

2

∘

f

1

∘ ( ∘ ) = ∘ ∘

f

(6)

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=147b17ea48b38d015319bca8a6d8a588