Rozdzial 05 - Funkcje boolowskie

(1)

Matematyka Dyskretna

Andrzej Szepietowski

(2)

(3)

Rozdział 1

Funkcje boolowskie

1.1 Algebra Boole’a

Najprostszym przykładem algebry Boole’a jest zbiór dwuelementowy:

B= {0, 1},

z trzema operacjami: alternatyw¸a, koniunkcj¸a i negacj¸a.

Alternatywa, któr¸a b¸edziemy te˙z nazywa´c po prostu sum¸a, jest operacj¸a dwuargumentow¸a,

oznaczan¸a przez:

p+ q lub p∨ q,

i okre´slon¸a przez tabel¸e:

p q p+q

0 0 0

0 1 1

1 0 1

1 1 1

Koniunkcja (lub iloczyn) jest drug¸a operacj¸a dwuargumentow¸a, oznaczan¸a przez:

p· q lub p∧ q,

p q p· q 0 0 0 0 1 0 1 0 0 1 1 1 3

(4)

Podobnie jak w arytmetyce, kropk¸e b¸edziemy opuszcza ´c, je˙zeli nie b¸edzie to prowadzi´c do niejednoznaczno´sci.

Operacje alternatywy i koniunkcji mo˙zna te˙z zdefiniowa´c za pomoc¸a nast¸epuj¸acych wzorów:

p+ q = max{p, q}, p· q = min{p, q}.

Negacja jest operacj¸a jednoargumentow¸a, oznaczan¸a przez:

¬p lub p,¯

p ¬p

0 1

1 0

Algebr¸e B= {0, 1} mo˙zemy interpretowa´c jako logik¸e zdaniow¸a. Zmienne s¸a zdaniami,

które mog¸a przyjmowa´c warto´sci prawda lub fałsz. Je˙zeli oznaczymy prawd¸e przez1 i

fałsz przez0, to powy˙zej zdefiniowane operacje odpowiadaj¸a znanym operacjom z logiki

zda´n.

Lemat 1.1 Operacje alternatywy, koniunkcji i negacji spełniaj¸a w algebrze B = {0, 1}

nast¸epuj¸ace to˙zsamo´sci:

(a) p+ q = q + p, pq= qp (alternatywa i koniunkcja s¸a przemienne), (b) p+ (q + r) = (p + q) + r, (pq)r = p(qr) (alternatywa i koniunkcja s¸a

ł¸aczne),

(c) (p + q)r = pr + qr (alternatywa jest rozdzielna wzgl¸edem koniunkcji), (d) (pq) + r = (p + r)(q + r) (koniunkcja jest rozdzielna wzgl¸edem alternatywy), (e) p+ 0 = p, p· 0 = 0, p+ 1 = 1, p· 1 = p,

(f) p+ p = p, p+ ¬p = 1, pp= p, p· ¬p = 0,

(g) p+ (pq) = p, p(p + q) = p (prawa pochłaniania),

(h) ¬(p + q) = ¬p · ¬q, ¬(pq) = ¬p + ¬q (prawa de’Morgana), (i) ¬¬p = p (prawo podwójnego przeczenia).

Najprostsze dowody powy˙zszych to˙zsamo´sci polegaj¸a na sprawdzeniu, ˙ze zachodz¸a one dla ka˙zdego mo˙zliwego podstawienia za zmienne warto´sci 1 lub 0. Na przykład, udowod-nimy to˙zsamo´s´c:

p+ pq = p.

(5)

1.1. Algebra Boole’a 5 p q p+ pq 0 0 0 0 1 0 1 0 1 1 1 1

Poniewa˙z trzecia kolumna jest identyczna z pierwsz¸a, wi¸ec równo´s´c p+ pq = p jest

prawdziwa dla ka˙zdego podstawienia, czyli jest to˙zsamo´sci¸a.

1.1.1 Algebra podzbiorów

Innym przykładem algebry Boole’a jest zbiór2X_{wszystkich podzbiorów jakiego´s zbioru}

X z operacjami okre´slonymi w nast¸epuj¸acy sposób: • A + B jest sum¸a mnogo´sciow¸a A∪ B • A · B jest iloczynem A∩ B

• ¬A jest uzupełnieniem zbioru, ¬A = X − A, • 1 jest całym zbiorem X,

• 0 jest zbiorem pustym ∅.

Wszystkie równo´sci z Lematu 1.1 s ˛a to˙zsamo´sciami w algebrze podzbiorów2X_{, to}

zna-czy s ˛a spełnione przy dowolnym podstawieniu podzbiorów za zmienne p, q i r. Na przy-kład dla dowolnych podzbiorów A, B⊂ X zachodzi A + AB = A. Rzeczywi´scie, je˙zeli

element x nale˙zy do zbioru A, to nale˙zy tak˙ze do sumy A+AB. Je˙zeli za´s x nie nale˙zy do A, to nie nale˙zy tak˙ze do iloczynu AB, a wi¸ec x nie nale˙zy do ˙zadnego składnika sumy A+ AB, czyli nie nale˙zy do A + AB. Tak wi¸ec zbiory A i A + AB zawieraj¸a dokładnie

te same elementy, a wi¸ec s¸a równe.

1.1.2 Alternatywa wykluczaj ˛

aca, xor

Oprócz trzech podstawowych, w algebrze Boole’a definiuje si¸e inne operacje. Dla nas wa˙zna b¸edzie operacja xor (ang. exclusive or) albo alternatywa wykluczaj¸aca. xor jest operacj¸a dwuargumentow¸a, oznaczan¸a przez:

p⊕ q

p q p⊕ q

0 0 0

0 1 1

1 0 1

(6)

Operacja ta jest nazywana alternatyw¸a wykluczaj¸ac¸a, poniewa˙z w logice zdaniowej zdanie p⊕ q jest prawdziwe, je˙zeli albo p, albo q jest prawdziwe, ale nie jest prawdziwe,

gdy p i q naraz s¸a prawdziwe. Operacj¸e xor mo˙zna zdefiniowa ´c poprzez alternatyw¸e, koniunkcj¸e i negacj¸e:

p⊕ q = p¯q+ ¯pq.

W algebrze podzbiorów operacja xor jest ró˙znic ˛a symetryczn ˛a

A⊕ B = (A − B) ∪ (B − A).

Lemat 1.2 Nast˛epuj ˛ace równo´sci s ˛a to˙zsamo´sciami w algebrze B= {0, 1} oraz w

alge-brze podzbiorów2X_:

(a) p⊕ q = q ⊕ p (przemienno´s´c xora), (b) (p ⊕ q) ⊕ r = p ⊕ (q ⊕ r) (ł¸aczno´s´c xora),

(c) (p ⊕ q)r = pr ⊕ qr (xor jest rozdzielne wzgl¸edem koniunkcji), (d) x⊕ 0 = x, x⊕ 1 = ¯x, x⊕ x = 0, x⊕ ¯x= 1,

(e) Je˙zeli x⊕ y = 0, to x = y.

Ł¸aczno´s´c operacji⊕ pozwala opuszcza´c nawiasy w wyra˙zeniach typu (q ⊕ q) ⊕ r bez

powodowania niejednoznaczno´sci.

1.2 Wyra˙zenia boolowskie

Podobnie jak wyra˙zenia arytmetyczne, mo˙zemy budowa ´c wyra˙zenia boolowskie. Wyra-˙zeniami boolowskimi s¸a stałe0 i 1 oraz zmienne boolowskie x, y, z,... Bardziej zło˙zone

wyra˙zenia mo˙zna budowa´c za pomoc¸a operatorów boolowskich i nawiasów. Je˙zeli U i W s¸a dwoma wyra˙zeniami boolowskimi, to wyra˙zeniami boolowskimi s¸a tak˙ze nast¸epuj¸ace wyra˙zenia:

U+ W, U· W, U⊕ W, ¬U, (U ).

Przykład 1.3 Przykładami wyra˙ze´n boolowskich s ˛a:

((x + ¬y) · (¬x + 1) + z) + ¬y (1 ⊕ x) · (y + 0)

xy+ yz + xz,

gdzie x, y oraz z s ˛a zmiennym boolowskimi.

Je˙zeli w wyra˙zeniu boolowskim za zmienne podstawimy warto´sci0 lub 1, to całe

wyra-˙zenie przyjmie jak ˛a´s warto´s´c,0 lub 1.

Przykład 1.4 W poni˙zszej tabeli zebrano warto´sci wyra˙zenia

xy+ yz + xz

(7)

1.2. Wyra˙zenia boolowskie 7 x y z xy+ yz + xz 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1

Jak wida´c wyra˙zenie U(x, y, z) = xy + yz + xz opisuje funkcj˛e, która ka˙zdemu

wek-torowi z{0, 1}3 _{przypisuje warto´s´c ze zbioru}_{{0, 1}. Podobnie dowolne inne}

wyra˙ze-nie boolowskie W(x1, . . . , xn) ze zmiennymi x1, . . . , xnopisuje funkcj˛e, która ka˙zdemu

wektorowi z{0, 1}n_{przypisuje warto´s´c ze zbioru}_{{0, 1}.}

Wyra˙zenie boolowskie W(x1, . . . , xn) mo˙ze te˙z by´c rozpatrywane w algebrze

pod-zbiorów2X_{. Wtedy za zmienne podstawiamy podzbiory X i warto´s´c wyra˙zenia te˙z jest}

podzbiorem X.

Przykład 1.5 Niech X = {1, 2, 3, 4, 5} i niech W (x, y, z) = xy + yz + xz b˛edzie

wyra˙zeniem boolowskim. Po podstawieniu x= {1, 4, 5}, y = {1, 2, 4} oraz z = {3, 4}

wyra˙zenie otrzyma warto´s´c W(x, y, z) = {1, 4}.

1.2.1 Wyra˙zenia boolowskie w j¸ezyku Pascal

W j¸ezyku Pascal wyra˙zeniami boolowskimi s¸a stałetruei false oraz zmienne ty-puboolean. Wyra˙zenia boolowskie mo˙zna te˙z budować z wyra˙zeń arytmetycznych za pomoça tak zwanych operatorów relacyjnych. Je˙zeliUiWs¸a dwoma wyra˙zeniami aryt-metycznymi, to wyra˙zeniem boolowskim jest wyra˙zenie:

U op W,

gdzieopoznacza dowolny operator relacyjny. Operatory relacyjne s¸a zestawione w tabeli: operator znaczenie

= równe

< mniejsze

> wi¸eksze

<> ró˙zne

<= mniejsze lub równe

>= wi¸eksze lub równe

Wyra˙zenia boolowskie mo˙zna tak˙ze budowa´c za pomoc¸a operatorów boolowskich i na-wiasów. Je˙zeliUiWs¸a dwoma wyra˙zeniami boolowskimi, to wyra˙zeniami boolowskimi s¸a tak˙ze nast¸epuj¸ace wyra˙zenia:

• U or W (suma lub alternatywa),

(8)

• not W (negacja),

• U xor W (exclusive or lub alternatywa wykluczaj¸aca),

• (U) (wyra˙zenieUwzi¸ete w nawias).

Przykładami wyra˙ze ´n boolowskich w j¸ezyku Pascal s¸a:

• true or b,

• b and not(x>=0),

• (0<=x) and (x<=10),

• (0<x) or (x>10).

gdziebjest zmienn¸a typu boolean, ax— zmienn¸a liczbow¸a.

Wyra˙zenia boolowskie wyst¸epuj¸a w j¸ezyku Pascal w instrukcjach warunkowych lub w p¸etlach while i repeat.

1.3 Funkcje boolowskie

Funkcja boolowska n zmiennych to dowolna funkcja typu

f : Bn _{→ B,}

gdzie B= {0, 1}. Funkcja f ka˙zdemy ci ˛agowi argumentów(x1, . . . , xn) ∈ Bn

przypi-suje warto´s´c f(x1, . . . , xn) ∈ B. Na przykład tabela

x y z f(x, y, z) 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1

opisuje funkcj˛e boolowsk ˛a, która przyjmuje warto´sci0 dla wektorów (0, 0, 0), (0, 1, 0)

oraz(0, 1, 1) oraz warto´s´c 1 dla wszystkich innych wektorów. W podrozdziale o

wyra-˙zeniach boolowskich pokazali´smy, ˙ze funkcje boolowskie mog ˛a być opisane za pomoc ˛a wyra˙zeń boolowskich. Na przykład funkcja f(x, y, z) z powy˙zszej tabeli mo˙ze być

opi-sana przez wyra˙zenie

(9)

1.3. Funkcje boolowskie 9

1.3.1 Funkcje boolowskie jednej zmiennej

Mamy cztery funkcje boolowskie jednej zmiennej:

• funkcj¸e stał¸a f0równ¸a 0,

• identyczno´s´c f1,

• negacj¸e f2,

• funkcj¸e stał¸a f3równ¸a 1.

Warto´sci tych funkcji zestawiono w tabeli:

x f0(x) f1(x) f2(x) f3(x)

0 0 0 1 1

1 0 1 0 1

S¸a to wszystkie funkcje boolowskie jednej zmiennej, poniewa˙z s¸a to funkcje ze zbioru B w zbiór B, a takich funkcji jest:

|B||B|= 22= 4.

1.3.2 Funkcje boolowskie dwóch zmiennych

Funkcji boolowskich dwóch zmiennych jest:

222 = 24= 16.

Ich warto´sci zestawiono w tabeli:

x y f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f13 f14 f15

0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1

0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1

1 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1

1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1

Zauwa˙zmy, ˙ze ci¸ag warto´sci ka˙zdej z tych funkcji czytany od góry do dołu stanowi zapis binarny jej numeru. Przyjrzyjmy si¸e bli˙zej tym funkcjom:

• f0= 0 jest funkcj¸a stał¸a równ¸a 0,

• f15= 1 jest funkcj¸a stał¸a równ¸a 1,

• f1(x, y) = xy jest koniunkcj¸a,

• f7(x, y) = x + y jest alternatyw¸a,

(10)

• f13(x, y) = (x ⇒ y) = y + ¯x jest implikacj¸a z x do y,

• f11(x, y) = (y ⇒ x) = x + ¯y jest implikacj¸a z y do x,

• f9(x, y) = (x ⇔ y) = ¬(x ⊕ y) = xy + ¯x¯y jest równowa˙zno´sci¸a,

• f3(x, y) = x jest rzutem na pierwsz¸a współrz¸edn¸a,

• f5(x, y) = y jest rzutem na drug¸a współrz¸edn¸a,

• f10(x, y) = ¬y jest negacj¸a drugiej współrz¸ednej,

• f12(x, y) = ¬x jest negacj¸a pierwszej współrz¸ednej,

• f14(x, y) = ¬(xy) jest zaprzeczeniem koniunkcji, tak zwany nand,

• f8(x, y) = ¬(x + y) jest zaprzeczeniem alternatywy, tak zwany nor,

• f2(x, y) = ¬(x ⇒ y) = x¯y jest zaprzeczeniem implikacji z x do y,

• f4(x, y) = ¬(y ⇒ x) = ¯xy jest zaprzeczeniem implikacji z y do x.

Jak widać, ka˙zd¸a z tych funkcji mo˙zna przedstawić za pomoça koniunkcji, alternatywy i negacji.

1.3.3 Alternatywa i koniunkcja n zmiennych

W tym i nast˛epnych podrozdziałach przedstawimy dalsze przykłady funkcji boolowskich. Alternatywa n zmiennych OR(x1, . . . , xn) = n _ i=1 xi= x1+ · · · + xn

przyjmuje warto´s´c0 tylko wtedy, wszystkie zmienne od x1do xnprzyjmuj ˛a warto´s´c0.

Koniunkcja n zmiennych AN D(x1, . . . , xn) = n ^ i=1 xi= x1· · · xn

przyjmuje warto´s´c1 tylko wtedy, wszystkie zmienne od x1do xnprzyjmuj ˛a warto´s´c1.

1.3.4 Funkcja progowa

Funkcja Tn k(x1, . . . , xn) =   

1, gdy liczba jedynek w´sród x1, . . . , xn jest

równa lub wi¸eksza od k,

(11)

1.3. Funkcje boolowskie 11

jest funkcj¸a progow¸a o n zmiennych z progiem k. B¸edziemy zakłada ´c, ˙ze1 ≤ k ≤ n.

Mówi ˛ac inaczej warto´s´c funkcji progowej T_kn(x1, . . . , xn) osi ˛aga warto´s´c1, je˙zeli liczba

jedynek w´sród (warto´sci) argumentów x1, ..., xnosi ˛agnie lub przekroczy próg k.

Funkcji progowe dwóch zmiennych s¸a proste.

T12(x, y) = x + y, T22(x, y) = x · y.

Proste te˙z s ˛a funkcje progowe trzech zmiennych

T₁3(x, y, z) = x + y + z, T₂3(x, y, z) = xy + yz + xz, T₃3(x, y, z) = x · y · z.

Przypu´sćmy, ˙ze mamy ju˙z wyra˙zenia dla funkcji progowych n zmiennych. Za ich pomoça mo˙zemy skonstruować wyra˙zenia dla funkcji progowych n+ 1 zmiennych.

T_n+1n+1(x1, . . . , xn, xn+1) = n+1 ^ i=1 xi, T₁n+1(x1, . . . , xn, xn+1) = n+1 _ i=1 xi. Je˙zeli1 < k ≤ n, to: T_kn+1(x1, . . . , xn, xn+1) = Tkn(x1, . . . , xn) + Tk−1n (x1, . . . , xn) · xn+1.

Ostatnia równo´s´c wyra˙za prosty fakt, ˙ze próg k jest osi ˛agni˛ety w´sród zmiennych x1, ...,

xn, xn+1, je˙zeli jest osi ˛agni˛ety w´sród zmiennych x1, ..., xn lub je˙zeli xn+1 = 1 i w´sród

zmiennych x1, ..., xnjest k− 1 jedynek.

1.3.5 Postacie normalne funkcji boolowskich

Nasuwa si¸e pytanie, czy ka˙zd¸a funkcj¸e n zmiennych mo˙zna przedstawi ´c za pomoc¸a ko-niunkcji, alternatywy i negacji. Odpowied´z jest pozytywna. Najpierw przykład. Rozpa-trzmy funkcj¸e boolowsk¸a trzech zmiennych:

x y z f(x,y,z) 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 0 1 1 1 0

(12)

Rozwa˙zmy wyra˙zenie:

¯ xyz.¯

Przyjmuje ono warto´s´c 1 tylko dla jednego wektora(0, 0, 1), czyli dla podstawienia x = 0, y = 0, z = 1. Podobnie, wyra˙zenie ¯xyz przyjmuje warto´s´c 1 tylko dla wektora(0, 1, 1),

wyra˙zenie xy¯z — tylko dla¯ (1, 0, 0), a wyra˙zenie x¯yz — tylko dla(1, 0, 1). Suma tych

wyra˙ze´n:

¯

xyz¯ + ¯xyz+ x¯yz¯+ x¯yz (1.1) przyjmuje warto´s´c 1 tylko dla wektorów(0, 0, 1), (0, 1, 1),(1, 0, 0), (1, 0, 1), czyli jest

równowa˙zna naszej funkcji f . Wyra˙zenie (1.1) jest w tak zwanej dysjunkcyjnej postaci

normalnej (DNF).

Funkcj¸e f mo˙zna te˙z opisa´c w innej formie. Rozwa˙zmy wyra˙zenie:

x+ y + z.

Przyjmuje ono warto´s´c 0 tylko dla jednego wektora(0, 0, 0), czyli dla podstawienia x = 0, y = 0, z = 0. Podobnie, wyra˙zenie (x + ¯y+ z) przyjmuje warto´s´c 0 tylko dla wektora (0, 1, 0), wyra˙zenie (¯x+ ¯y+ z) — tylko dla (1, 1, 0), a wyra˙zenie (¯x+ ¯y+ ¯z) — tylko

dla(1, 1, 1). Iloczyn tych wyra˙ze ´n:

(x + y + z)(x + ¯y+ z)(¯x+ ¯y+ z)(¯x+ ¯y+ ¯z),

przyjmuje warto´s´c zero tylko dla wektorów(0, 0, 0), (0, 1, 0), (1, 1, 0), i (1, 1, 1),

czy-li jest równowa˙zny funkcji f . Jest to tak zwana koniunkcyjna posta´c normalna (CNF) funkcji f .

Metod¸e t¸e mo˙zna uogólni´c na funkcje n zmiennych. Wprowadzimy oznaczenie:

x1= x x0= ¯x.

Dla dowolnego wektora a ∈ {0, 1}n_{, niech a}_{(i) oznacza i-t¸a współrz¸edn¸a wektora a.}

Rozwa˙zmy teraz wyra˙zenie:

ma(x) = xa(1)1 · x a(2)

2 . . . xa(n)n .

Zauwa˙zmy, ˙ze ma(x) jest równe 1 tylko wtedy, gdy podstawimy xi = a(i), dla ka˙zdego

i, czyli dla x= a. Wida´c z tego, ˙ze:

f(x) = _

a∈f−1(1)

ma(x).

Jest to dysjunkcyjna postać normalna (DNF) funkcji f (sumowanie oznacza tutaj alternatyw¸e). Aby otrzymać postać koniukcyjn¸a, zaczynamy od wyra˙zenia:

sa(x) = x¬a(1)1 + x ¬a(2)

2 + · · · + x¬a(n)n .

Zauwa˙zmy, ˙ze sa(x) jest równe 0 tylko wtedy, gdy podstawimy: xi= a(i), dla ka˙zdego

i, czyli dla x= a. Wida´c z tego, ˙ze:

f(x) = ^

a∈f−1(0)

sa(x).

(13)

1.4. Wielowarto´sciowe funkcje boolowskie 13

1.4 Wielowarto´sciowe funkcje boolowskie

Mo˙zemy te˙z rozpatrywa´c wielowarto´sciowe funkcje boolowskie, które ci ˛agom bitów przy-pisuj ˛a ci ˛agi bitów, czyli funkcje typu

f : Bn_{→ B}m_.

Ci ˛agowi argumentów

x1, . . . , xn

funkcja f przypisuje ci ˛ag warto´sci

(f1(x1, . . . , xn), . . . , fm(x1, . . . , xn)),

gdzie f1,..., fms ˛a jednowarto´sciowymi funkcjami boolowskimi. Wielowarto´sciowe

funk-cje boolowskie mo˙zna traktowa´c jak ci ˛agi jednowarto´sciowych funkcji. Przykładem wie-lowarto´sciowej funkcji boolowskiej jest funkcja sortuj ˛aca

S(x, y, z) = (T13(x, y, z), T23(x, y, z), T33(x, y, z)).

Warto´sci tej funkcji zestawione s ˛a w nast˛epuj ˛acej tabeli:

x y z S(x, y, z) 0 0 0 000 0 0 1 100 0 1 0 100 0 1 1 110 1 0 0 100 1 0 1 110 1 1 0 110 1 1 1 111

Jak wida´c funkcja S sortuje ci ˛ag wej´sciowy ustawiaj ˛ac go w porz ˛adku nierosn ˛acym.

1.5 Sieci boolowskie

Najpierw przykład. Na rysunku 1.1 przedstawiono pewn¸a sie ´c boolowsk¸a. Jest to graf skierowany z sze´scioma wierzchołkami (bramkami) i pi¸ecioma kraw¸edziami ł¸acz¸acymi niektóre bramki. W tym i nast¸epnych przykładach przyjmujemy, ˙ze kraw¸edzie s¸a skiero-wane od góry do dołu. Bramki maj¸a etykiety. Jedna etykietowana jest stał¸a1, dwie

ety-kietowane s¸a zmiennymi x i y, a trzy etyety-kietowane s¸a operatorami logicznymi,∧, ∨ i ¬.

Bramki oznaczone stałymi lub zmiennymi s¸a bramkami wej´sciowymi i ˙zadne kraw¸edzie nie prowadz¸a do nich. Bramka¬ ma jedn¸a kraw¸ed´z wchodz¸ac¸a, a bramki ∨ i ∧ po dwie.

Bramka∨ jest bramk¸a wyj´sciow¸a, bo nie wychodzi z niej ˙zadna kraw¸ed´z. Z ka˙zd¸a bramk¸a

(14)

Rysunek 1.1: Przykład sieci boolowskiej ∨ ∧ x 1 ¬ y

lub zmienn¸a, tym wyra˙zeniem jest ta stała lub ta zmienna. Z bramk¸a∧ zwi¸azane jest

wy-ra˙zenie x∧ 1, z bramk¸a ¬ wyra˙zenie ¬y, a z bramk¸a ∨ wyra˙zenie (1 ∧ x) ∨ ¬y.

Sie´c oblicza funkcj˛e boolowsk ˛a. Najpierw podstawiamy warto´sci0 lub 1 za zmienne

wej´sciowe, na przykład niech x = 0 i y = 1. W pierwszym kroku, obliczaj ˛a swoje warto´sci bramki z etykietami ∧ i ¬. Bramka ∧ daje warto´s´c 0 ∧ 1 = 0, a bramka ¬

warto´s´c¬1 = 0. W drugim kroku swoj ˛a warto´s´c oblicza bramka wyj´sciowa0 ∨ 0 = 0 i

jest to warto´s´c, któr ˛a zwraca cała sie´c dla wej´scia x= 0 oraz y = 1. Oczywi´scie funkcja

obliczana przez t ˛a sie´c jest opisana przez wyra˙zenie(1 ∧ x) ∨ ¬y przypisane bramce

wyj´sciowej.

Ogólnie, sieć boolowska to acykliczny (bez cykli) graf skierowany, którego wierz-chołki nazywamy bramkami. Ka˙zda bramka ma swoj¸a etykiet¸e, któr¸a mo˙ze by ć stała 1 lub 0, zmienna lub operator boolowski. W naszych rozwa˙zaniach ograniczymy si¸e do czterech operatorów:∧, ∨, ¬ i ⊕, ale mo˙zna rozwa˙zać sieci z innym zbiorem

operato-rów. Do bramek oznaczonych stałymi lub zmiennymi nie prowadz¸a ˙zadne kraw¸edzie, s¸a to bramki wej´sciowe. Bramki oznaczone przez¬ maj¸a po jednej kraw¸edzi wej´sciowej, a

bramki z pozostałymi operatorami maj¸a po dwie kraw¸edzie wchodz¸ace. Wierzchołek, z którego nie wychodz¸a ˙zadne kraw¸edzie, nazywamy wyj´sciowym. W sieci mo˙ze by´c kilka bramek wyj´sciowych.

Z ka˙zd¸a bramk¸a u w sieci mo˙zemy zwi¸aza´c wyra˙zenie boolowskie W(u). Robimy to

przez indukcj¸e ze wzgl¸edu na struktur¸e sieci:

• Najpierw przypisujemy wyra˙zenia bramkom wej´sciowym. W tym wypadku

wyra-˙zeniem tym jest etykieta bramki u: stała lub zmienna.

• Je˙zeli bramka u jest etykietowana negacj¸a ¬ i dochodzi do niej kraw¸ed´z od bramki v oraz bramka v ma ju˙z przypisane wyra˙zenie W(v), to bramce u przypisujemy

wyra˙zenie W(u) = ¬W (v).

• Je˙zeli etykiet¸a bramki u jest operator dwuargumentowy op, to do u prowadz¸a kraw¸edzie

od dwóch bramek, v i w. Je˙zeli przypisano ju˙z wyra˙zenia W(v) i W (w) bramkom v i w, to bramce u przypisujemy wyra˙zenie W(u) = W (v) op W (w).

(15)

1.5. Sieci boolowskie 15

Liczb¸e wszystkich bramek w sieci nazywamy kosztem sieci, a długo´sć najdłu˙zszej ´scie˙zki w sieci nazywamy gł¸eboko´sci¸a sieci. Z ka˙zd ˛a bramk ˛a wyj´sciow ˛a u, zwi ˛azana jest funkcja opisana przez wyra˙zenia W(u) i mo˙zemy powiedzieć, ˙ze sieć oblicza wyra˙zenie W(u). Z faktu, ˙ze ka˙zd¸a funkcj¸e boolowsk¸a mo˙zna przedstawić w postaci normalnej

wy-nika, ˙ze ka˙zd¸a funkcj¸e boolowsk¸a mo˙zna przedstawi ´c za pomoc¸a sieci. Jednak konstruk-cja sieci dla funkcji boolowskiej f poprzez wyznaczanie postaci normalnej zazwyczaj prowadzi do sieci o du˙zym koszcie (liczbie bramek). Poni˙zej omówiono przykłady sieci o stosunkowo małym koszcie.

1.5.1 Sie´c dla alternatywy kilku zmiennych

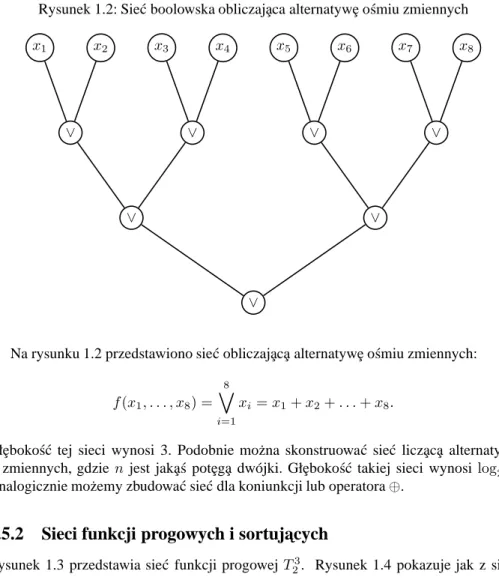
Rysunek 1.2: Sie´c boolowska obliczaj¸aca alternatyw¸e o´smiu zmiennych

∨ ∨ ∨ x1 x2 ∨ x3 x4 ∨ ∨ x5 x6 ∨ x7 x8

Na rysunku 1.2 przedstawiono sie´c obliczaj¸ac¸a alternatyw¸e o´smiu zmiennych:

f(x1, . . . , x8) = 8

_

i=1

xi= x1+ x2+ . . . + x8.

Gł¸eboko´sć tej sieci wynosi 3. Podobnie mo˙zna skonstruować sieć licz¸aça alternatyw¸e

n zmiennych, gdzie n jest jak¸a´s pot¸eg¸a dwójki. Gł¸eboko´s´c takiej sieci wynosilog2n.

Analogicznie mo˙zemy zbudowa´c sie´c dla koniunkcji lub operatora⊕.

1.5.2 Sieci funkcji progowych i sortuj ˛

acych

(16)

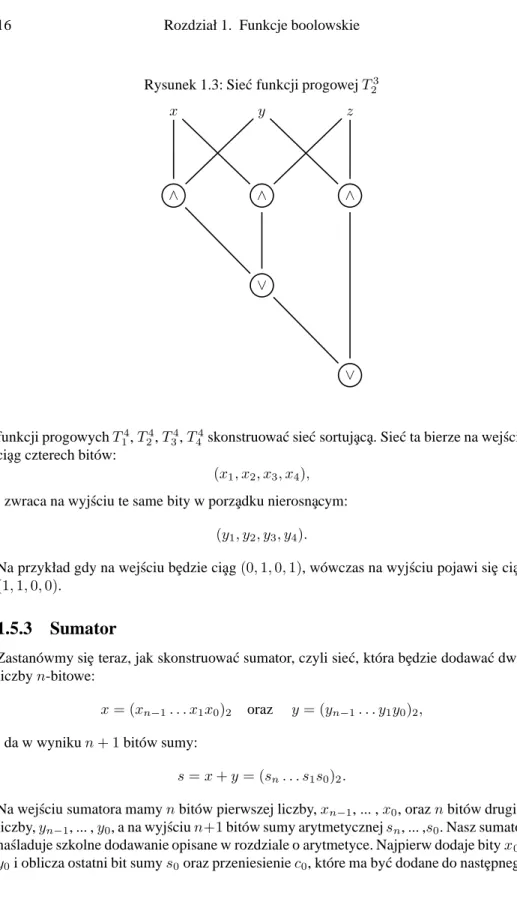
Rysunek 1.3: Sie´c funkcji progowej T₂3

x y z

∧ ∧ ∧

∨

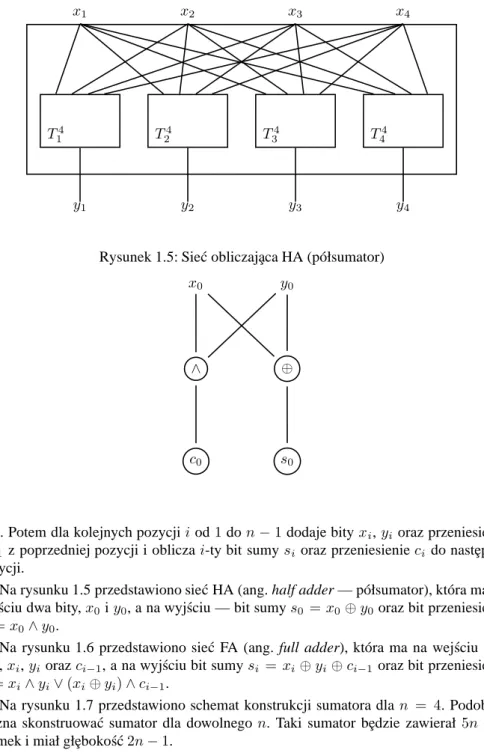
funkcji progowych T₁4, T₂4, T₃4, T₄4skonstruować sieć sortuj¸aça. Sieć ta bierze na wej´sciu ci¸ag czterech bitów:

(x1, x2, x3, x4),

i zwraca na wyj´sciu te same bity w porz¸adku nierosn¸acym:

(y1, y2, y3, y4).

Na przykład gdy na wej´sciu b¸edzie ci¸ag(0, 1, 0, 1), wówczas na wyj´sciu pojawi si¸e ci¸ag (1, 1, 0, 0).

1.5.3 Sumator

Zastanówmy si¸e teraz, jak skonstruować sumator, czyli sieć, która b¸edzie dodawać dwie liczby n-bitowe:

x= (xn−1. . . x1x0)2 oraz y= (yn−1. . . y1y0)2,

i da w wyniku n+ 1 bitów sumy:

s= x + y = (sn. . . s1s0)2.

Na wej´sciu sumatora mamy n bitów pierwszej liczby, xn−1, ... , x0, oraz n bitów drugiej

liczby, yn−1, ... , y0, a na wyj´sciu n+1 bitów sumy arytmetycznej sn, ... ,s0. Nasz sumator

na´sladuje szkolne dodawanie opisane w rozdziale o arytmetyce. Najpierw dodaje bity x0i

(17)

1.5. Sieci boolowskie 17

Rysunek 1.4: Schemat sieci sortuj¸acej

x4 x3 x2 x1 T44 T34 T24 T14 y4 y3 y2 y1

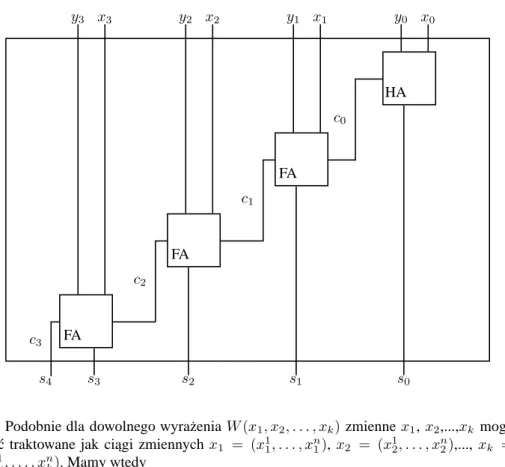
Rysunek 1.5: Sie´c obliczaj¸aca HA (półsumator)

x0 y0

∧ ⊕

c0 s0

bitu. Potem dla kolejnych pozycji i od1 do n − 1 dodaje bity xi, yi oraz przeniesienie

ci−1 z poprzedniej pozycji i oblicza i-ty bit sumy si oraz przeniesienie ci do nast¸epnej

pozycji.

Na rysunku 1.5 przedstawiono sie´c HA (ang. half adder — półsumator), która ma na wej´sciu dwa bity, x0i y0, a na wyj´sciu — bit sumy s0 = x0⊕ y0oraz bit przeniesienia

c0= x0∧ y0.

Na rysunku 1.6 przedstawiono sie´c FA (ang. full adder), która ma na wej´sciu trzy bity, xi, yi oraz ci−1, a na wyj´sciu bit sumy si = xi⊕ yi⊕ ci−1 oraz bit przeniesienia

ci= xi∧ yi∨ (xi⊕ yi) ∧ ci−1.

Na rysunku 1.7 przedstawiono schemat konstrukcji sumatora dla n = 4. Podobnie

mo˙zna skonstruowa´c sumator dla dowolnego n. Taki sumator b¸edzie zawierał5n − 3

(18)

Rysunek 1.6: Sie´c obliczaj¸aca FA

xi yi ci−1

∧ ⊕

∨ ∧ ⊕

ci si

1.6 Operacje boolowskie na wektorach

Operacje boolowskie mo˙zna wykonywa´c tak˙ze na ci¸agach bitów okre´slonej długo´sci, czy-li na elementach zbioru

Bn = {0, 1}n.

Dla dwóch ci¸agów:

x= (x1, x2, . . . , xn) oraz y= (y1, y2, . . . , yn),

operacje koniunkcji, alternatywy, xor i negacji wykonywane s¸a po współrz¸ednych:

x· y = (x1· y1, x2· y2, . . . , xn· yn),

x+ y = (x1+ y1, x2+ y2, . . . , xn+ yn),

x⊕ y = (x1⊕ y1, x2⊕ y2, . . . , xn⊕ yn),

¬x = (¬x1,¬x2, . . . ,¬xn).

Mo˙zemy te˙z oblicza´c bardziej zło˙zone wyra˙zenia na ci ˛agach bitów. Na przykład

0 · x + y · z = (0 · x1+ y1· z1, . . . ,0 · xn+ yn· zn),

gdzie z jest wektorem z= (z1, . . . , zn). Niezbyt formalnie mo˙zna powiedzie´c, ˙ze warto´s´c

(19)

1.6. Operacje boolowskie na wektorach 19

Rysunek 1.7: Schemat sumatora

y0 x0 y1 x1 y2 x2 y3 x3 HA FA FA FA s0 s1 s2 s4 s3 c0 c1 c2 c3

Podobnie dla dowolnego wyra˙zenia W(x1, x2, . . . , xk) zmienne x1, x2,...,xk mog ˛a

by´c traktowane jak ci ˛agi zmiennych x1 = (x11, . . . , xn1), x2 = (x12, . . . , xn2),..., xk =

(x1

k, . . . , xnk). Mamy wtedy

W(x1, x2, . . . , xk) = (W (x11, x12. . . , x1k), W (x 2

1, x22. . . , x2k), . . . , W (xn1, xn2. . . , xnk)).

Je˙zeli wektor zerowy(0, 0, . . . , 0) oznaczymy przez 0, a wektor zło˙zony z samych

jedy-nek(1, 1, . . . , 1) — przez 1, to zachodz¸a wszystkie to˙zsamo´sci z lemat.ow 1.1 oraz 1.2.

1.6.1 Reprezentacja zbioru

Ci¸agi bitów z Bn= {0, 1}n_{mog¸a słu˙zy´c do reprezentacji podzbiorów zbioru}

{1, 2, . . . , n}.

Ci¸ag x∈ {0, 1}n_{nale˙zy traktowa´c jako funkcj¸e charakterystyczn¸a pewnego podzbioru.}

Wtedy operacje boolowskie na ci¸agach odpowiadaj¸a operacjom na zbiorach. Alternatywa odpowiada sumie zbiorów, koniunkcja cz¸e´sci wspólnej, a negacja uzupełnieniu zbioru. Operacja xor odpowiada ró˙znicy symetrycznej.

(20)

Podobnie dla dowolnego wyra˙zenia W(x1, . . . , xk) za zmienne x1,...,xk mo˙zemy

podstawia´c podzbiory A1,...,Akotrzymuj ˛ac podzbiór W(A1, . . . , Ak) lub ci ˛agi

reprezen-tuj ˛ace funkcje charakterystyczne tych zbiorów χ1,...,χkotrzymuj ˛ac ci ˛ag W(χ1, . . . , χk),

który jest funkcj ˛a charakterystyczn ˛a zbioru W(A1, . . . , Ak).

Przykład 1.6 Niech X= {1, 2, 3, 4, 5} oraz niech W (x, y, z) = x · 1 + y · (¬z). Je˙zeli

za zmienne podstawimy podzbiory x = {3, 5}, y = {1, 2, 4, 5} oraz z = {2, 3, 5}. to

warto´s´c wyra˙zenia b˛edzie zbiorem W(x, y, z) = {1, 3, 4, 5}.

Je˙zeli za zmienne podstawimy funkcje charakterystyczne tych samych podzbiorów

x = (0, 0, 1, 0, 1), y = (1, 1, 0, 1, 1) oraz z = (0, 1, 1, 0, 1), to warto´s´c wyra˙zenia

b˛edzie ci ˛agiem W(x, y, z) = (1, 0, 1, 1, 1), który jest funkcj ˛a charakterystyczn ˛a zbioru

{1, 3, 4, 5}.

Przykład 1.7 W grupie8 studentów s ˛a uprawiaj ˛acy koszykówk˛e, siatkówk˛e lub pływanie. Niech ci ˛ag K = (1100 1010) reprezentuje koszykarzy, ci ˛ag S = (1010 0011) siatkarzy,

a ci ˛ag P = (1010 0011) pływaków. Wtedy ci ˛ag

• K · S · P = (1000 0010) reprezentuje studentów, którzy uprawiaj ˛a wszystkie trzy sporty,

• ¬(K + S + P ) = (0001 0100) studentów, którzy nie uprawiaj ˛a ˙zadnego sportu,

• K · (¬S) · (¬P ) = (0100 1000) studentów, którzy uprawiaj ˛a tylko koszykówk˛e,

• K · S + S · P + K · P = (1010 0011) studentów, którzy uprawiaj ˛a co najmniej dwie dyscypliny sportu.

Przypominamy, ˙ze wyra˙zenie K· S + S · P + K · P opisuje funkcj˛e progow ˛a T₂3.

1.6.2 To˙zsamo´sci w algebrze podzbiorów

Zastanówmy si˛e, kiedy równo´s´c pomi˛edzy dwoma wyra˙zeniami

U(x1, . . . , xn) = V (x1, . . . , xn)

jest to˙zsamo´scia w algebrze podbiorów2X_{, to znaczy zachodzi dla dowolnych}

podsta-wie´n podzbiorów za zmienne x1,...,xk. Zachodzi nast˛epuj ˛ace

Twierdzenie 1.8 Równo´s´c pomi˛edzy dwoma wyra˙zeniami

U(x1, . . . , xk) = V (x1, . . . , xk)

jest to˙zsamo´sci ˛a w algebrze podzbiorów2X_{wtedy i tylko wtedy, gdy jest to˙zsamo´sci ˛}_{a w}

algebrze{0, 1}.

Z tego wynika, ˙ze aby sprawdzić to˙zsamo´sć, wystarchy sprawdzić, czy zachodzi ona dla podstawień zbioru pustego∅ lub całego zbioru X za zmienne.

(21)

1.6. Operacje boolowskie na wektorach 21

Dowód: Po pierwsze, zauwa˙zmy, ˙ze równo´s´c U(x1, . . . , xk) = V (x1, . . . , xk) jest

rów-nowa˙zna równo´sci U(x1, . . . , xk) ⊕ V (x1, . . . , xk) = 0. Mo˙zemy, wi˛ec ograniczy´c

roz-wa˙zania do równo´sci

W(x1, . . . , xk) = 0 (1.2)

Załó˙zmy, ˙ze równo´s´c (1.2) jest to˙zsamo´sci ˛a w algebrze {0, 1}, czyli przy ka˙zdym

podstawieniu0 lub 1 za zmienne warto´s´c wyra˙zenia jest równa 0. Je˙zeli teraz podstawimy

za zmienne ci ˛agi x1= (x11, . . . , xn1),...,xk= (x1k, . . . , xnk), to otrzymamy

W(x1, . . . , xk) = (W (x11, . . . , x1k), ..., W (xn1, . . . , xnk)).

ale dla ka˙zdej współrz˛ednej i,1 ≤ i ≤ n zachodzi W(xi1, . . . , xik) = 0,

poniewa˙z równo´s´c (1.2) jest to˙zsamo´sci ˛a w algebrze {0, 1}, a zmienne xi

1, . . . , xik ∈

{0, 1}. Mamy wi˛ec

W(x1, . . . , xk) = (W (x11, . . . , x1k), ..., W (xn1, . . . , xnk)) = (0, . . . , 0).

Tak wi˛ec, przy ka˙zdym podstawieniu za zmienne ci ˛agów lub funkcji charakterystycz-nych otrzymujemy wektor zerowy, czyli funkcj˛e charakterystyczn ˛a zbioru pustego. Rów-no´s´c (1.2) jest wi˛ec to˙zsamo´sci ˛a w algebrze podzbiorów.

Je˙zeli równo´s´c (1.2) jest to˙zsamo´sci ˛a w algebrze podzbiorów, to jest spełniona przy ka˙zdym podstawieniu zbiorów∅ lub X, a to oznacza, ˙ze równo´s´c jest to˙zsamo´sci ˛a w algebrze{0, 1}, gdy˙z operacje na zbiorach ∅ i X s ˛a takie same jak na stałych0 i 1.

1.6.3 Operacje na wektorach w j¸ezyku Pascal

W j¸ezyku Pascal (i w wielu innych j˛ezykach) operacje boolowskie:and, or, xor, neg, mo˙zna stosowa´c do liczb typu integer lub innych typów całkowitych (byte, shor-tint, word lub longint). Liczba traktowana jest wtedy jako ci¸ag bitów jej przedstawienia binarnego. Na przykład:

13 and 6=4

poniewa˙z 13 jest reprezentowane przez:

(0000000000001101),

6 przez:

(0000000000000110)

oraz:

(0000 0000 0000 1101)and(0000 0000 0000 0110) =(0000 0000 0000 0100), a ten ostatni ci¸ag reprezentuje 4 w typie integer. Podobnie zachodzi:

(22)

Przykład 1.9 Je˙zeli chcemy reprezentowa´c w pami¸eci komputera uło˙zenie kamieni w

grze w warcaby na 64-polowej szachownicy, to wystarcz¸a dwie liczby typu longint (po 32 bity). W jednej liczbie reprezentujemy poło˙zenie czarnych, a w drugiej poło˙zenie bia-łych kamieni (w grze w warcaby kamienie mog¸a le˙ze´c tylko na 32 czarnych polach).

Taka reprezentacja ma dwie zalety. Zajmuje mało pami¸eci i operacje na zbiorach s¸a wykonywane bardzo szybko, poniewa˙z operacje boolowskie s¸a operacjami niskiego po-ziomu.

1.6.4 Szyfrowanie w systemie one-pad

Operacje boolowskie na wektorach mo˙zna wykorzysta´c do szyfrowania. W systemie szy-frowania „one-pad” wiadomo´s´c x i klucz k s¸a ci¸agami bitów x, k∈ {0, 1}n_(Je˙zeli

wia-domo´sć jest ci¸agiem znaków, to kodujemy ka˙zdy znak jako 8 bitów i cały ci¸ag mo˙ze by ć traktowany jako ci ˛ag bitów). Zaszyfrowana wiadomo´sć ma postać:

y= C(k, x) = x ⊕ k.

Zauwa˙zmy, ˙ze deszyfrowa´c mo˙zna według tego samego wzoru:

D(k, y) = y ⊕ k,

poniewa˙z

y⊕ k = (x ⊕ k) ⊕ k = x ⊕ (k ⊕ k) = x ⊕ 0 = x,

System one-pad mo˙zna stosować w nast¸epuj¸acy sposób: Najpierw przesyła si¸e bezpieczn¸a poczt¸a (na przykład kuriersk¸a) zapasy kluczy, na przykład notesy z kartkami, gdzie ka˙zda strona zawiera jeden klucz. Nast¸epnie szyfrowane depesze mog¸a by ć przesyłane mniej bezpiecznymi kanałami. Trzeba tylko przestrzegać zasady, ˙ze jedna kartka mo˙ze być u˙zy-ta tylko raz (st¸ad angielska nazwa systemu). Same klucze powinny by ć losowane, aby przeciwnik nie mógł ich odgadn¸ać.

Zalet¸a tego systemu jest to, ˙ze jest on absolutnie bezpieczny. Zróbmy nast¸epuj¸acy eksperyment. Przypu´sćmy, ˙ze kto´s ma zaszyfrowan¸a wiadomo´sć y i chce j¸a odszyfrować przez odgadni¸ecie samej wiadomo´sci x. Zastanówmy si¸e, dla jakich ci¸agów x istnieje klucz k, taki ˙ze x⊕ k = y, czyli inaczej, jakie wiadomo´sci mog¸a być zaszyfrowane w y. Okazuje si¸e, ˙ze dla ka˙zdego ci¸agu x ∈ {0, 1}n _{istnieje klucz k, taki ˙ze x}_{⊕ k = y.}

Wystarczy wzi¸a´c k= x ⊕ y. Mamy wtedy:

C(k, x) = x ⊕ k = x ⊕ (x ⊕ y) = (x ⊕ x) ⊕ y = 0 ⊕ y = y.

Wad¸a tego systemu jest to, ˙ze klucze musz¸a być tej samej długo´sci co sama wiadomo´sć i musz¸a być trzymane w sekrecie. Powoduje to kłopoty z przesyłaniem i przechowywaniem kluczy.

Łami¸ac szyfry cz¸esto korzysta si¸e z faktu, ˙ze wiadomo´sci, lub ich fragmenty, wyst¸epuj¸a z ró˙zn¸a cz¸esto´sci¸a (prawdopodobie ´nstwem). Przypu´s´cmy dla prostoty, ˙ze szyfrujemy po-jedyncze znaki i niech{0, 1}8_{b¸edzie zbiorem wiadomo´sci (kody ASCII). Dla}

normal-nych tekstów (listów) rozkład cz¸esto´sci poszczególnormal-nych znaków jest bardzo niejednostaj-ny. Kody jednych liter wyst¸epuj¸a du˙zo cze´sciej, ni˙z innych, a pewne znaki nie wyst¸epuj¸a

(23)

1.7. Funkcja parzysto´sci (parity) 23

wcale. Gdyby´smy teraz zastosowali jaki´s prymitywny sposób kodowania bez klucza, gdzie ka˙zdy znak x zawsze jest szyfrowany za pomoc¸a D(x), to w zaszyfrowanej

wia-domo´sci rozkład cz¸esto´sci b¸edzie podobny. Najcz¸e´sciej wyst¸epuj¸acy znak w wiawia-domo´sci zaszyfrowanej odpowiada najcz¸e´sciej wyst¸epuj¸acemu znakowi w tek´scie, itd. Mo˙zna to wykorzysta´c przy łamaniu szyfrów.

Jak zaraz zobaczymy w przypadku szyfrów one-pad tak nie jest. Znaki w zaszyfrowa-nej wiadomo´sci posiadaj¸a rozkład

jednostajny, tak jakby´smy losowali kolejne znaki i dlatego analiza statystyczna jest tutaj bezu˙zyteczna.

Niech X = {0, 1}n_{b¸edzie zbiorem wiadomo´sci z dowolnym rozkładem}

prawdopo-dobie´nstwa, a K= {0, 1}n_{zbiorem kluczy z jednostajnym rozkładem prawdopodobie}

ń-stwa. Losujemy wiadomo´sć x∈ X i klucz k ∈ K i obliczamy wiadomo´sć y = x ⊗ k ∈ {0, 1}n_{. Niech A}

xoznacza zdarzenie, ˙ze wylosowano wiadomo´s´c x, Kk, ˙ze wylosowano

klucz k, a Cy zdarzenie, ˙ze otrzymano zaszyfrowan¸a wiadomo´s´c y. Zgodnie ze wzorem

na prawdopodobie ´nstwo całkowite mamy

P(Cy) =

X

x∈{0,1}n

P(Cy|Ax) · P (Ax),

P(Cy|Ax) jest prawdopodobie´nstwem warunkowym, ˙ze zaszyfrowan ˛a wiadomo´sci ˛a

b˛e-dzie y pod warunkiem, ˙ze zaszyfrowano wiadomo´s´c x. Jak pokazali´smy wy˙zej tylko dla jednego klucza k= x ⊗ y, y = x ⊗ k. Dlatego P (Cy|Ax) = ₂1n oraz

P(Cy) = 1 2n X x∈{0,1}n P(Ax) = 1 2n.

1.7 Funkcja parzysto´sci (parity)

Zdefiniujmy funkcj¸e boolowsk¸a parzysto´sci (parity):

P ar: {0, 1}n_{→ {0, 1},} P ar(x) = n M i=1 xi = x1⊕ x2⊕ . . . ⊕ xn.

Funkcja P ar jest addytywna, to znaczy:

P ar(x ⊕ y) = P ar(x) ⊕ P ar(y),

co wynika z faktu, ˙ze operacja⊕ jest ł¸aczna i przemienna.

P ar(x) jest równa 1, je˙zeli liczba jedynek w ci¸agu x jest nieparzysta, oraz jest równa

0, je˙zeli w ci¸agu x liczba jedynek jest parzysta. Je˙zeli b¸edziemy uto˙zsamia ´c wektor x ze zbiorem, to P ar(x) jest równe parzysto´sci mocy zbioru x.

Twierdzenie 1.10 P ar(x) = 1 dla dokładnie połowy wej´s´c. To znaczy: |{x ∈ {0, 1}n _{: P ar(x) = 1}| = 2}n−1_.

(24)

Pierwszy dowód. Twierdzenie wynika z faktu, ˙ze dokładnie połowa podzbiorów zbioru

{1, 2, . . . , n} jest nieparzystej mocy.

Drugi dowód. We´zmy wektor:

s= (1, 0, . . . , 0),

który ma jedynk¸e tylko na pierwszej współrz¸ednej. Zdefiniujemy teraz funkcj¸e h:

h(x) = x ⊕ s.

Funkcja h ł¸aczy elementy zbioru{0, 1}n_{w pary, poniewa˙z je˙zeli h}_{(x) = y, to h(y) = x.}

Rzeczywi´scie:

h(y) = y ⊕ s = (x ⊕ s) ⊕ s = x ⊕ (s ⊕ s) = x ⊕ 0 = x.

Ponadto:

P ar(x) ⊕ P ar(y) = P ar(x ⊕ y) = P ar(x ⊕ x ⊕ s) = P ar(s) = 1,

a st¸ad wynika, ˙ze dla ka˙zdej pary x, y = h(x) dokładnie jedna z dwóch liczb P ar(x), P ar(y) jest jedynk¸a, czyli dla dokładnie połowy x ∈ {0, 1}n_{, P ar}_{(x) = 0.} ₂

1.8 Odciski, zabezpieczanie danych

Funkcja P ar jest wykorzystywana do kontroli, czy dane nie zostały przekłamane pod-czas przesyłania lub przechowywania. Przypu´sćmy, ˙ze Małgosia chce przesłać Jasiowi wiadomo´sć x∈ {0, 1}n_{i chce choć troch¸e zabezpieczyć x przed przekłamaniem. Wtedy}

Małgosia wysyła x razem z bitem P ar(x) — jego odciskiem. Odcisk wiadomo´sci ma

pełnić podobn ˛a rol˛e co odcisk palca u człowieka, ma pomóc w identykikacji. Przypu´sć-my teraz, ˙ze Ja´s dostał wiadomo´sć y z odciskiem P ar(x). Dla prostoty zakładamy, ˙ze

odcisk P ar(x) nie został przekłamany, na przykład Małgosia i Ja´s mog¸a si¸e umówi´c, ˙ze

przesyłaj¸a sobie tylko takie wiadomo´sci x, dla których P ar(x) = 0. Aby sprawdzi´c, czy

wiadomo´s´c nie została przekłamana, Ja´s oblicza P ar(y) i porównuje go z P ar(x). Je˙zeli P ar(x) 6= P ar(y), to Ja´s ma pewno´s´c, ˙ze x 6= y. Je˙zeli P ar(x) = P ar(y), to Ja´s

przyj-muje, ˙ze x= y, cho´c w tym przypadku nie mo˙ze mie´c pewno´sci. Zauwa˙zmy, ˙ze je˙zeli x

i y ró˙zni¸a si¸e tylko na jednym bicie, to x⊕ y ma tylko jedn¸a jedynk¸e, wi¸ec: P ar(x ⊕ y) = 1.

Z drugiej strony:

P ar(x ⊕ y) = P ar(x) ⊕ P ar(y),

z czego wynika:

P ar(x) 6= P ar(y).

Tak wi¸ec je˙zeli w przesyłanych danych zostanie zmieniony (przekłamany) jeden bit, b¸edzie mo˙zna to wykry´c porównuj¸ac P ar(x) z P ar(y).

(25)

1.8. Odciski, zabezpieczanie danych 25

Jest to bardzo stary system kontroli danych. Działa on dobrze, je˙zeli przekłamania s¸a przypadkowe i prawdopodobie ństwo przekłamania dwóch bitów jest du˙zo mniejsze ni˙z prawdopodobie ństwo przekłamania jednego bitu. Funkcja P ar jest jednak zbyt prosta, aby zabezpieczyć dane przed zło´sliwym przekłamywaniem. Wystarczy bowiem zawsze przekłamywać parzyst¸a liczb¸e bitów, aby rzecz si¸e nie wykryła.

Poka˙zemy teraz bardziej zło˙zony sposób zabezpieczania danych przed przekłama-niem. Dla dowolnego wektora r ∈ {0, 1}n _{zdefiniujmy funkcj¸e parzysto´sci z}

parame-trem: P arr: {0, 1}n→ {0, 1}, P arr(x) = P ar(x · r) = n M i=1 xiri.

Funkcja P arroblicza parzysto´s´c liczby bitów wektora x, ale liczone s¸a tylko bity na

po-zycjach wyznaczonych przez jedynki wektora r, inaczej — P arr(x) to parzysto´s´c

prze-kroju x i r.

Funkcja P arrjest addytywna:

P arr(x ⊕ y) = P ar((x ⊕ y) · r) = P ar(x · r ⊕ y · r)

= P ar(x · r) ⊕ P ar(y · r) = P arr(x) ⊕ P arr(y).

Twierdzenie 1.11 Je˙zeli x6= 0, to dla dokładnie połowy r ∈ {0, 1}n_{zachodzi P ar} r(x) =

0.

Dowód. Poniewa˙z x6= 0, wi˛ec istnieje wektor s z jedn¸a jedynk¸a, taki ˙ze: x· s = s.

Wektor s powinien mie´c jedynk¸e na pozycji, na której x te˙z ma jedynk¸e. Podobnie jak w dowodzie twierdzenia 1.10, mo˙zemy teraz okre´sli´c funkcj¸e:

h(r) = r ⊕ s,

która „zlepia” wektory z{0, 1}n_{w pary. Ponadto mamy:}

h(r) · x = (r ⊕ s) · x = r · x ⊕ s · x = r · x ⊕ s.

Z tego wynika, ˙ze:

P arh(r)(x) = P ar(h(r) · x) = P ar(r · x ⊕ s)

= P ar(r · x) ⊕ P ar(s) = P arr(x) ⊕ 1,

a st¸ad — ˙ze dla ka˙zdej pary, r, h(r), dokładnie jedna z dwóch liczb P arr(x), P arh(r)(x)

(26)

Wykorzystuj¸ac funkcje P arr, mo˙zna zbudowa´c lepszy system zabezpieczania

da-nych. Na pocz¸atku Małgosia i Ja´s zaopatruj¸a si¸e w ci¸ag wylosowanych kluczy:

r1, r2, . . . , rs∈ {0, 1}n.

Klucze te powinny być trzymane w sekrecie. Je˙zeli teraz Małgosia chce przesłać Jasio-wi Jasio-wiadomo´sć x, to bierze kolejny klucz r z ci¸agu r1, r2, . . . , rs i wysyła x razem z

odciskiem P arr(x). Ja´s po odebraniu wiadomo´sci y razem z odciskiem P arr(x) (tak

jak poprzednio zakładamy, ˙ze P arr(x) nie jest przekłamywane) porównuje P arr(x) i

P arr(y).

Je˙zeli x= y, to dla ka˙zdego r:

P arr(x) = P arr(y).

Je˙zeli za´s x6= y, to x ⊕ y 6= 0 i dla połowy wektorów r mamy: P arr(x) ⊕ P arr(y) = P arr(x ⊕ y) = 1,

a wi¸ec dla połowy wektorów r mamy:

P arr(x) 6= P arr(y).

Tak wi¸ec z prawdopodobie ´nstwem1₂Ja´s wykryje, ˙ze x6= y.

Aby zwi¸ekszyć to prawdopodobie ństwo mo˙zna brać kilka kolejnych kluczy r1, . . . , rk.

Wtedy w przypadku, gdy x6= y, prawdopodobie ´nstwo, ˙ze dla ka˙zdego i = 0, . . . , k,

b˛e-dzie P arri(x) = P arri(y), jest równe 2

−k_.

1.9 Zadania

1. Które z poni˙zszych równo´sci s¸a to˙zsamo´sciami w algebrze B= {0, 1}:

a) p+ qr = q + pr; b)(p + q)r = p + qr; c)(r ⊕ q)r = r ⊕ qr;

d)(p + q)r = pr(q + r) + qr; e) (p ⊕ q) ⊕ p = p ⊕ q?

Które z tych równo´sci s ˛a to˙zsamo´sciami w algebrze2X_?

2. Udowodnij lematy 1.1 i 1.2.

3. Przedstaw za pomoc ˛a tabeli funkcje: a) g(p, q, r) = (p ⊕ q)r; b) h(x, y, z) = (x + ¬y) · (y + ¬z); c) f(u, v, w, x) = uv + wx.

4. Napisz wyra˙zenia dla wszystkich funkcji progowych czterech zmiennych.

5. Jaki zbiór przedstawia wyra˙zenie W(x, y, z) = xy + xz + yz, je˙zeli podstawimy x= {1, 2, 5}, y = {1, 3, 4}, z = {2, 3, 5}?

6. Niech X b˛edzie zbiorem studentów, K podzbiorem studentów graj ˛acych w koszy-kówk˛e, S studentów graj ˛acych w siatkówk˛e, P uprawiaj ˛acych pływanie. Przedstaw wyra˙zenie boolowskie opisuj˛ece nast˛epu ˛ace podzbiory:

(27)

1.9. Zadania 27

• studentów uprawiaj ˛acych tylko jedn ˛a dyscyplin˛e sportu,

• studentów uprawiaj ˛acych dokładnie dwie dyscypliny sportu,

• koszykarzy, którzy nie pływaj ˛a.

7. Udowodnij, ˙ze wszystkie funkcje boolowskie dwóch zmiennych mo˙zna przedsta-wi´c za pomoc¸a: a) dwóch operatorów, koniunkcji i negacji (lub alternatywy i ne-gacji); b) jednego operatora nand (lub nor).

8. Ile jest funkcji boolowskich typu f : Bn_{→ B?}

9. Ile funkcji f: B2_{→ B spełnia równanie xf (x, y) = yf (x, y)?}

Wskazówka. Rozwa˙z wyra˙zenie xf(x, y) ⊕ yf (x, y).

10. Funkcja f : B3 _{→ B przyjmuje warto´s´c 1 tylko dla wektorów (1, 0, 0), (0, 1, 0)}

oraz(0, 0, 1). Przedstaw funkcj¸e f w postaciach normalnych (dysjunkcyjnej i

ko-niunkcyjnej).

11. Narysuj sie´c boolowsk¸a dla funkcji z poprzedniego zadania. 12. Zaprojektuj sie´c, która:

• odejmuje od siebie dwie liczby w postaci dwójkowej. • mno˙zy dwie liczby dwubitowe.

• dla wej´scia x1, x2, x3zlicza liczb˛e jedynek i przedstawi ˛a j ˛a w postaci

dwój-kowej.

• traktuje wej´scie x1, x0 jako liczb˛e w postaci dwójkowej i daje na wyj´sciu

y1, y2, y3tyle jedynek ile wynosi liczba(x1x0)2.

13. Jaki ci ˛ag przedstawia wyra˙zenie W(x, y, z) = xy + xz + yz, je˙zeli podstawimy x= (0, 1, 0, 1, 1, 0, 0), y = (1, 1, 1, 1, 0, 0, 0), z = (0, 1, 1, 1, 0, 1, 0)?

14. Oblicz warto´s´c wyra˙ze´n x or y, x and y, not x, x xor y: a) je˙zeli zmiennexiys¸a typu shortint i przyjmuj¸a warto´sci: x=6, y=-3, b) je˙zeli zmiennexiys¸a typu byte i przyjmuj¸a warto´sci: x=6, y=3. 15. Dany jest wektor x= (0, 1, 1). Dla jakich wektorów r ∈ B3_{, P ar}

r(x) = 1?

16. Dane s¸a dwa wektory: x = (0, 1, 0) oraz y = (0, 0, 1). Dla jakich wektorów r ∈ B3_{, P ar}

(28)

1.10 Problemy

1.10.1 Gra w kamienie

Rozwa˙zmy nast˛epuj ˛ac ˛a gr˛e. Mamy trzy kupki kamyków. Gracze po kolei zabieraj ˛a ka-mienie z kupek, przy czym wolno bra´c kaka-mienie tylko z jednej kupki i oczywi´scie jakie´s kamienie trzeba zabra´c. Wygrywa gracz, który zabiera ostatnie kamienie.

Gra ta posiada prost ˛a strategi˛e wygrywaj ˛ac ˛a. Niech x, y i z oznaczaj ˛a liczby kamieni w poszczególnych kupkach. Wtedy układ kamieni x, y, z jest:

• wygrywaj ˛acy, je˙zeli x⊕ y ⊕ z 6= 0 • przegrywaj ˛acy, je˙zeli x⊕ y ⊕ z = 0.

Je˙zeli pocz ˛atkowy układ jest wygrywaj ˛acy, to gracz zaczynaj ˛acy gr˛e wygra, je˙zeli zawsze przeka˙ze przeciwnikowi układ przegrywaj ˛acy.

Udowodnij, ˙ze

• W ˙zadnym układzie przegrywaj ˛acym nie mo˙zna wygra ´c w jednym ruchu.

• Ka˙zdy układ przegrywaj ˛acy po wykonaniu dowolnego ruchu staje si˛e wygrywaj ˛acy.

• Ka˙zdy układ wygrywaj ˛acy mo˙zna doprowadzi´c za pomoc ˛a jednego ruchu do ukła-du przegrywaj ˛acego.

Wskazówka. We´zmy wygrywaj ˛acy układ x, y, z. Niech r= x ⊕ y ⊕ z 6= 0 i niech i b˛edzie

najwy˙zszym bitem, na którym r ma jedyk˛e. Wtedy jedna z liczb, powiedzmy x, te˙z ma jedynk˛e na pozycji i i zachodzi x⊕ r < x, oraz (x ⊕ r) ⊕ y ⊕ z = 0.

Czy podobn ˛a stategi˛e mo˙zna stosowa´c, je˙zeli jest wi˛ecej kupek kamieni?

1.10.2 Posta´c normalna

Udowodnij, ˙ze dla ka˙zdej funkcji funkcji f : Bn _{→ B istnieje dokładnie jeden wektor:}

a= (aA)A⊂{1,...,n}, taki ˙ze: f(x) = M A⊂{1,...,n} aA· ^ i∈A xi.