Symbole oznaczone i nieoznaczone w granicy ciągu

Symbole oznaczone i

nieoznaczone w granicy

ciągu

Autorzy:

Katarzyna Czyżewska

2019

Symbole oznaczone i nieoznaczone w granicy ciągu

Symbole oznaczone i nieoznaczone w granicy ciągu

Autor: Katarzyna Czyżewska

Na wyrazach dwóch lub więcej ciągów możemy wykonywać działania arytmetyczne otrzymując nowy ciąg. Jeżeli ciągi wyjściowe były zbieżne, to analogiczne działania arytmetyczne można również wykonywać na granicach właściwych tych ciągów, ale także na granicach niewłaściwych otrzymując symbole graniczne ujmowane w nawisy kwadratowe, dla zaznaczenia, że nie są to działania wykonywane na liczbach, tylko na granicach. Niektóre z tych symboli dają zawsze ten sam wynik, bez względu na to jakie ciągi składowe dają określony symbol graniczny i nazywamy je symbolami oznaczonymi. Niektóre znów dają różne wyniki w zależności od tego, na jakich ciągach wykonujemy działania i takie symbole nazywamy nieoznaczonymi.

DEFINICJA

Definicja 1: Symbol oznaczony i nieoznaczony

Definicja 1: Symbol oznaczony i nieoznaczony

Symbolem oznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i które daje zawsze taki sam wynik zależny tylko od granic ciągów, z których powstaje symbol graniczny. Symbolem nieoznaczonym nazywamy wyrażenie algebraiczne, które jest umownym zapisem działań wykonywanych na granicach i którego wartości nie da się jednoznacznie obliczyć na podstawie jedynie granic ciągów, z których powstaje symbol graniczny.

UWAGA

Uwaga 1:

Uwaga 1:

Do obliczania symboli oznaczonych służą odpowiednie twierdzenia podające wartości konkretnych symboli granicznych. Nie istnieją natomiast ogólne twierdzenia pozwalające obliczyć wartość symbolu nieoznaczonego i w każdym przypadku indywidualnie należy, stosując odpowiednie przekształcenie algebraiczne, zamienić symbol nieoznaczony na oznaczony.

2,0 10 20 30 1,0 0,5 1,5 2,5 3,0 40 50 60 70 80

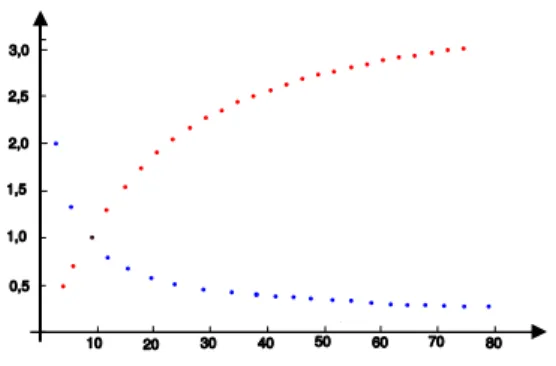
Rysunek 1: Interpretacja geometryczna symbolów oznaczonych i

Rys. 1 przedstawia dwa ciągi, z których jeden (czerwony) powstaje z drugiego (niebieskiego) poprzez operację odwrócenia wyrazów ciągu tzn. . Zauważamy, że jeżeli ciąg wyjściowy jest rozbieżny do , to ciąg odwrotności jego wyrazów jest zbieżny do zera i na odwrót, jeżeli ciąg wyjściowy o wyrazach dodatnich jest zbieżny do zera, to ciąg odwrotności jego wyrazów jest rozbieżny do . [ ]1 ∞ [ ]01+

=

b

n _a1_n

+∞

+∞

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: o symbolach oznaczonych

o symbolach oznaczonych

i i

Jeżeli , to oraz Jeżeli , to

PRZYKŁAD

Przykład 1:

Przykład 1:

Oblicz granicę . Rozwiązanie:

Zauważamy, że dla oraz, że .

Z twierdzenia o dwóch ciągach mamy

Czyli z twierdzenia o symbolach oznaczonych otrzymujemy .

PRZYKŁAD

Przykład 2:

Przykład 2:

Oblicz granicę . Rozwiązanie:

Zauważamy, że ciąg ma wyrazy dodatnie oraz, że . Rzeczywiście nierówność

jest równoważna nierówności , czyli, aby była spełniona definicja granicy wystarczy przyjąć .

Z twierdzenia o symbolach oznaczonych wnioskujemy więc, że .

[ ]

1

0

[ ]

∞

1

| | = 0

lim

n→∞

a

n

lim

n→∞ _{| |a}1_n

= +∞

∞

lim

n→∞

a

n

=

+−

lim

n→∞ _a1_n

= 0.

lim

n→∞ _{2 +n−1n}21

2 + n − 1 > n

n

2

_{n ∈ N}

_lim

_n→∞

_{n = +∞}

(2 + n − 1) = +∞.

lim

n→∞

n

2

= 0

lim

n→∞n _{2 +n−1n}21

lim

n→∞n _{sin ( )}11 n

sin ( )

1 n

lim

n→∞

| sin ( )| = 0

1n

| sin ( ) − 0| < ε

1 n

n >

arcsin ε1

= [

] + 1

n

0 _{arcsin ε}1

= +∞

lim

n→∞ _{sin ( )}11 n

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: o symbolach oznaczonych

o symbolach oznaczonych

Niech będzie dowolna liczbą rzeczywistą. Symbolami oznaczonymi są

gdzie symbol oznacza granicę ciągu o wyrazach dodatnich zbieżnego do zera, a symbol granicę ciągu o wyrazach ujemnych zbieżnego do zera.

PRZYKŁAD

Przykład 3:

Przykład 3:

Oblicz granicę Rozwiązanie:

Przekształcimy wyjściowe wyrażenie graniczne do znanego symbolu oznaczonego

a

[±∞ + a] = ±∞,

[a ⋅ (±∞)] = {

±∞

_∓∞

dla a > 0

_{dla a < 0}

,

[±∞ ⋅ (±∞)] = +∞,

[±∞ ⋅ (∓∞)] = −∞,

[

a

] = 0,

±∞

[ ] = {

a

,

0±

±∞

_∓∞

dla a > 0

_{dla a < 0}

[

∞

a

] = {

∞

,

0

dla a > 0

dla a < 0

[

∞

∞

] = ∞,

[ ]

0

+

_{[ ]}

₀

−

(3 − 2 + n − 4)

lim

n→∞

n

3

n

2

[∞ − ∞ + ∞ − 4]

(3 − 2 + n − 4) =

(3 − +

− ) = [∞ ⋅ (3 − 0 + 0 − 0)] = ∞

lim

n→∞

n

3

n

2

lim

n→∞

n

3 _n2 _n12 _n43

PRZYKŁAD

Przykład 4:

Przykład 4:

Oblicz granicę Rozwiązanie: Zauważamy, że . Obliczamy .

PRZYKŁAD

Przykład 5:

Przykład 5:

Oblicz granicę Rozwiązanie:

Jako pierwszą obliczamy granicę wykładnika w potędze znajdującej się w liczniku

Następnie wykorzystujemy odpowiedni symbol oznaczony do obliczenia granicy . Ostateczne obliczamy granicę

TWIERDZENIE

Twierdzenie 3:

Twierdzenie 3: o symbolach nieoznaczonych

o symbolach nieoznaczonych

Symbolami nieoznaczonymi są , , , , , ,

(

lim

n→∞ n+1 2 n+1

)

n

=

= [

] = ∞

lim

n→∞ n+1 2 n+1

lim

n→∞ n(1+ )1 n2 1+1 n ∞⋅(1+0) 1+0

(

= [

] = ∞

lim

n→∞ n+1 2 n+1

)

n

∞

∞

lim

n→∞ (2n+3) n+4 3−n 4 +3nn3

= [

] =

= [

] =

lim

n→∞ _3−2nn+4 _−∞∞

lim

n→∞ n(1+ ) 4 n n( −2)3 n 1+0 0−2 −21

(2n + 3

= [

] = 0

lim

n→∞

)

n+4 3−2n

∞

−21

= [[ ] = 0.

lim

n→∞ (2n+3) n+4 3−n 4 +3nn3 _∞0

[ ]

0 0

[ ]

∞∞

[0 ⋅ ∞] [∞ − ∞] [

∞

0

]

[ ]

0

0

[ ].

1

∞

PRZYKŁAD

Przykład 6:

Przykład 6:

Wykaż, że symbol jest nieoznaczony. Rozwiązanie:

Wiemy, że oraz .

Obliczamy dwie różne granice, które dają ten sam symbol nieoznaczony , ale różne wyniki końcowe

.

Świadczy to o tym, że nie da się w sposób jednoznaczny określić wartości symbolu .

PRZYKŁAD

Przykład 7:

Przykład 7:

Wykaż, że symbol jest nieoznaczony. Rozwiązanie:

Znajdziemy dwa ciągi, które dają ten sam symbol graniczny , ale różne wyniki końcowe uzyskane za pomocą prostego przekształcenia algebraicznego

Różne wyniki dowodzą, że nie da się w sposób jednoznaczny określić wartości symbolu .

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 05:02:27

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php?

[0 ⋅ ∞]

n =

= ∞

lim

n→∞

lim

n→∞

n

2

lim

n→∞ _n12

=

lim

n→∞ _n1

= 0

[[0 ⋅ ∞]

⋅ n = [0 ⋅ ∞] =

= 0

lim

n→∞ _n12

lim

n→∞ _n1

⋅

= [0 ⋅ ∞] =

n = ∞

lim

n→∞ _n1

n

2

lim

n→∞

[0 ⋅ ∞]

[∞ − ∞]

[∞ − ∞]

( − n) = [∞ − ∞] =

(1 − ) = [∞ ⋅ (1 − 0)] = ∞

lim

n→∞

n

3

lim

n→∞

n

3 _n12

(n − ) = [∞ − ∞] =

( − 1) = [∞ ⋅ (0 − 1)] = −∞.

lim

n→∞

n

3

lim

n→∞

n

3 1_n2

[∞ − ∞]

link=6cfddaf0f664a55c66a6a7541a77cac5