Układy dynamiczne. Klasyfikacja punktów stacjonarnych na płaszczyźnie

(1)

Układy dynamiczne.

Klasyfikacja punktów

stacjonarnych na

płaszczyźnie

Autorzy:

Vsevolod Vladimirov

2019

(2)

(1)

(2)

Układy dynamiczne. Klasyfikacja punktów stacjonarnych na płaszczyźnie

Autor: Vsevolod Vladimirov

Rozpatrzmy układ równań różniczkowych zwyczajnych, których prawe strony nie zależą od zmiennej :

Będziemy zakładać, że funkcje są różniczkowalne w sposób ciągły po wszystkich zmiennych Układ

Układ ( 1 )( 1 ) nazywa się układem autonomicznym, albo też układem dynamicznym nazywa się układem autonomicznym, układem dynamicznym.

DEFINICJA

Definicja 1:

Punkt nazywa się punktem stacjonarnympunktem stacjonarnym układu ( 1 ), jeżeli .

Zamiast pełnego układu ( 1 ), w małym otoczeniu punktu stacjonarnego można rozpatrywać jego linearyzacjęlinearyzację . Rozpatrzmy prawą

stronę tego układu. Każdą funkcję można w otoczeniu punktu przedstawić, zgodnie ze

wzorem Taylora, w postaci

gdzie oraz

Zatem zachodzi

LEMAT

Lemat 1:

Układ dynamiczny w otoczeniu punktu stacjonarnego da się przedstawić w postaci

gdzie

Układ

Układ (2) nazywa się linearyzacją układu dynamicznego (2) nazywa się linearyzacją układu dynamicznego ( 1 )( 1 ) w otoczeniu punktu stacjonarnego w otoczeniu punktu stacjonarnego . Okazuje się, że przy pewnych warunkach, rozwiązania układu ( 1 ) oraz rozwiąznia układu liniowego ( 2 ) są w małym otoczeniu

n

t

= ( , . . . , ) ;

d x1 d t

f

1

x

1

x

2

x

n

= ( , . . . , ) ;

d x2 d t

f

2

x

1

x

2

x

n

. . . .

= ( , . . . , ) .

d xn d t

f

n

x

1

x

2

x

n

, i = 1, . . . n,

f

i

x

i

.

(

x

1,0

,

x

2,0

, . . .

x

n,0

) ∈

R

n

(

,

, . . .

) = 0, i = 1, . . . n

f

i

x

1,0

x

2,0

x

n,0

( , , . . . )

f

i

x

1

x

2

x

n

(

x

1,0

,

x

2,0

, . . .

x

n,0

)

( , , . . . ) =

(

,

, . . .

) ( −

) + O(|ξ ),

f

i

x

1

x

2

x

n

∑

nk=1 _{∂ x}∂fi_k

x

1,0

x

2,0

x

n,0

x

k

x

k,0

|

2

ξ = ∑

n k=1

( −

x

k

x

k,0

)

2

−

−−−−−−−−−−−−

−

√

= 0.

lim

|ξ|→ 0 O(|ξ )|2 |ξ|

(

x

1,0

,

x

2,0

, . . .

x

n,0

)

=

+ O(|ξ ),

d d t

⎡

⎣

⎢⎢

⎢

ξ

1

ξ

2

. . . .

ξ

n

⎤

⎦

⎥⎥

⎥

⎡

⎣

⎢⎢

⎢

a

11

a

21

. . . .

a

n1

a

12

a

22

. . . . .

a

n2

. . .

. . . . .

. . .

a

1n

a

2n

. . . .

a

nn

⎤

⎦

⎥⎥

⎥

⎡

⎣

⎢⎢

⎢

ξ

1

ξ

2

. . . .

ξ

n

⎤

⎦

⎥⎥

⎥

|

2

=

−

,

=

(

,

, . . .

), i, j = 1, 2, . . . . n.

ξ

k

x

k

x

k,0

a

i,j _{∂ x}∂ fi_j

x

1,0

x

2,0

x

n,0

(

x

1,0

,

x

2,0

, . . .

x

n,0

)

(3)

(4)

(5)

(6) punktu stacjonarnego "jakościowo identyczne". Ponieważ rozwiązywać (analizować) układ liniowy jest na ogół niezmiernie prościej, niż układ pełny, opłaca się spróbować znaleźć warunki umożliwiające taką podmianę. To, czy zachowanie pełnego układu w otoczeniu punktu stacjonarnego jest rzeczywiście reprezentowane przez jego linearyzację, zależy od wartości własnych macierzy linearyzacji układu ( 2 ).

Przeanalizujemy to na przykładzie układu w , podając przy okazji klasyfikację prostych punktów stacjonarnych. Rozpatrzmy zatem układ równań

DEFINICJA

Definicja 2:

Zbiór zmiennych nazywamy płaszczyzną fazowąpłaszczyzną fazową układu ( 3 )

Portretem fazowym układu

Portretem fazowym układu ( 3 )( 3 ) nazywamy zbiór krzywych sparametryzowanych nazywamy zbiór krzywych sparametryzowanych

które tworzą rozwiązania

które tworzą rozwiązania tego układu.tego układu. Posługując się terminologią zapożyczoną w mechanice punktu materialnego, krzywe ( 4 ) nazywają też często trajektoriamitrajektoriami lub trajektoriami fazowymi.trajektoriami fazowymi.

Przystępujemy do klasyfikacji punktów stacjonarnych układu ( 3 ).

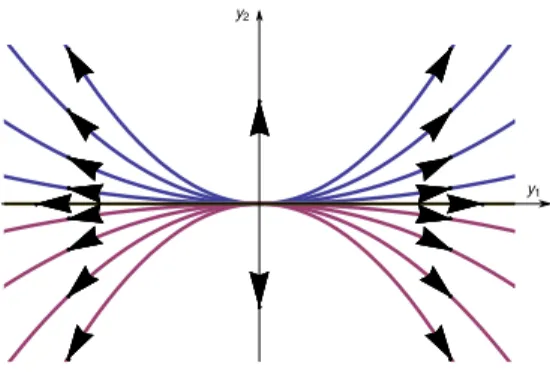
1. Przypadek, gdy wartości własne macierzy są rzeczywiste, różne, dodatnie.

Niech na przykład . Wtedy punkt przestrzeni fazowej nazywa się źródłemźródłem. Wówczas da się znaleźć taką liniową zamianę zmiennych

że układ ( 3 ) przybierze postać

Rozwiązaniem tego układu są wówczas funkcje

W przypadku, gdy , rozwiązanie to można przedstawić w postaci równoważnej, przedstawiając jako funkcję poprzez wyrugowanie :

gdzie

Portret fazowy układu ( 5 ) wygląda w tym przypadku tak, jak jest to pokazane na Rys. 1.

R

2

[ ] = [

] [ ] = [ ] .

d d t

_η

ξ

a

_a

11 21

a

12

a

22

ξ

η

A^ ξ

η

(ξ, η) ∈ R

2

C : { ξ = ξ[t],

_{η = η[t],}

,

λ

1

λ

2

A^

0 <

λ

1

<

λ

2

(0, 0)

[ ] = [

y

1

] [ ] ,

y

2

b

11

b

21

b

12

b

22

ξ

η

[ ] = [

] [ ] .

d d t

y

_y

1 2

λ

1

0

0 λ

2

y

1

y

2

=

,

=

.

y

1

C

1

e

λ1t

y

₂

C

₂

e

λ2t

≠ 0

C

1

y

2

y

1

t

=

,

y

2

C

3

y

λ2 λ1 1

=

⋅ {

C

3

C

2

1/

( )

C

1

gdy

> 0,

/ λ2λ1

_C

1

−1/ (| |

C

1

)

λ2/λ1

gdy

C

₁

< 0.

(4)

(7)

(8)

(9)

y1 y2

Rysunek 1: Portret fazowy układu (5)

Zwróćmy uwagę na to, że osie współrzędnych są trajektoriami fazowymi układu. Oś pozioma odpowiada przypadku , zaś oś pionowa odpowiada przypadkowi osobliwemu . Te dwie trajektorie fazowe nie są ujęte we wzorze ( 6 ).

2. Wartości własne macierzy są rzeczywiste, różne, ujemne.

Niech na przykład . Punkt przestrzeni fazowej nazywa się wówczas zlewemzlewem. Podobnie jak w przypadku poprzednim, istnieje liniowa zamiana zmiennych taka, że w nowych zmiennych układ ( 3 ) ma postać

Zauważmy teraz, że zamiana zmiennej niezależnej odzworowuje układ ( 7 ) w układ

równoważny układowi ( 5 ). Przekształcenie nazywa się odbiciem zmiennej czasowej. Prowadzi ono do tego, że ruch wzdłuż każdej trajektorii fazowej odbywa się w przeciwnym kierunku. Poza tym portret fazowy pozostaje bez zmian. Wynika stąd, że portret fazowy układu ( 7 ) będzie taki, jak pokazano na Rys. 2.

y1 y2

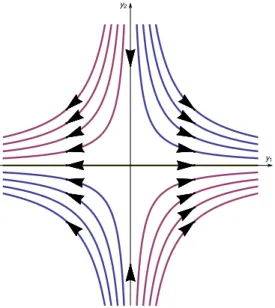
3. Przypadek gdy wartości własne macierzy są rzeczywiste, niezerowe i mają różne znaki. Niech, na przykład, . Wtedy punkt

przestrzeni fazowej nazywa się siodłemsiodłem. Wówczas istnieje liniowa zamiana zmiennych taka że w nowych zmiennych układ ( 3 ) ma postać

Rozwiązanie tego układu dane jest wzorami

W przypadku, gdy , rozwiązanie to można też przepisać w postaci równoważnej, przedstawiając jako funkcję poprzez wyrugowanie zmiennej :

= 0

C

2

= 0

C

1

,

λ

1

λ

2

A^

<

< 0

λ

2

λ

1

(0, 0)

(ξ, η) → ( , )

y

1

y

2

[ ] = [

] [ ] .

d d t

y

_y

1 2

λ

1

0

0 λ

2

y

1

y

2

t → τ = −t

[ ] = [

] [ ] ,

d d τ

y

_y

1 2

| |

λ

1

0

0 | |

λ

2

y

1

y

2

t → τ = −t

,

λ

1

λ

2

A^

> 0 >

λ

1

λ

2

(0, 0)

(ξ, η) → ( , )

y

1

y

2

[ ] = [

] [ ] .

d d t

y

_y

1 2

λ

1

0

0 −| |

λ

2

y

1

y

2

=

,

=

.

y

1

C

1

e

λ1t

y

2

C

2

e

−| | tλ2

≠ 0

C

1

y

2

y

1

t

=

,

2 3 −| / |λ2 λ1

(5)

(10)

(11)

(12) gdzie

Portret fazowy układu ( 9 ) w tym przypadku wygląda tak, jak to jest pokazane na Rys. 3. Zwrócmy uwagę na to, że osie współrzędnych są również trajektoriami fazowymi układu ( 10 ). Oś pozioma odpowiada przypadkowi ; oś pionowa odpowiada przypadku osobliwemu . Te dwie trajektorie fazowe nie są wyrażone poprzez wzór ( 9 )

y1 y2

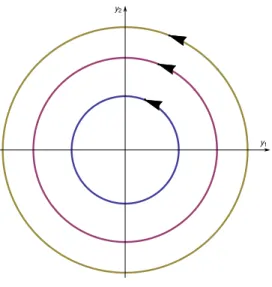
4. Przypadek gdy wartości własne macierzy są czysto urojone i róznią się znakiem: . W tym przypadku punkt przestrzeni fazowej nazywa się środkiem.środkiem. Istnieje liniowa zamiana zmiennych taka, że w nowych zmiennych układ ( 3 ) ma postać

Rozwiązanie tego układu dane jest wzorami

Rozwiązania te są funkcjami okresowymi. W płaszczyźnie fazowej na rysunku Rys. 4 są one przedstawione w postaci krzywych (orbit) zamkniętych.

=

,

y

2

C

3

y

1−| / |λ2 λ1

=

⋅ {

C

3

C

2

1/

( )

C

1

, gdy

> 0,

/ λ2λ1

C

1

−1/ (| |

C

1

)

λ2/λ1

, gdy

C

1

< 0.

= 0

C

2

= 0

C

1

,

λ

1

λ

2

A^

λ

1,2

= ± i ω

(0, 0)

(ξ, η) → ( , )

y

1

y

2

[ ] = [

] [ ] .

d d t

y

_y

1 2

0 ω

−ω

0 y

y

12

= A cos ωt + B sin ωt,

= ω[B cos ωt − A sin ωt] .

(6)

y1 y2

5. Przpadek gdy wartości własne macierzy są zespolone, czyli .

W tym przypadku punkt przestrzeni fazowej nazywa się ogniskiemogniskiem niestabilnym w przypadku gdy oraz stabilnym gdy .

Portret fazowy ogniska niestabilnego przedstawionno na Rys. 5. Portret fazowy ogniska stabilnego wygląda podobnie, przy czym trajektorie są tu skierowane do początku układu współrzędnych.

y1 y2

Rysunek 5: Obraz ogniska niestabilnego na płaszczyźnie fazowej.

Zachodzi

TWIERDZENIE

Twierdzenie 1:

Charakter punktów stacjonarnych oraz przebieg trajektorii w ich małym otoczeniu jakościowo nie zmienia się przy dodaniu członów nieliniowych, odrzuconych pod czas przejścia do układów zlinearyzowanych, dla wszystkich wymienionych przypadków za wyjątkiem środka.za wyjątkiem środka.

,

λ

1

λ

2

A^

λ

1,2

= α ± i ω

(0, 0)

α > 0

(7)

UWAGA

Uwaga 1:

Klasyfikację podobną do podanej dla przypadku stosuje się również do zlinearyzowanego układu -wymiarowego ( 2 ). Analog sformułowanego wyżej twierdzenia mówi, że układ wyjsciowy oraz jego linearyzacja posiadają podobne

jakościowo portrety fazowe w małym otoczeniu punktu stacjonarnego, gdy macierz linearyzacji nie posiada wartości własnyh o zerowych częściach rzeczywistych.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 07:29:29

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=a92c8b2d7fce12819fa6c15322184385

Autor: Vsevolod Vladimirov