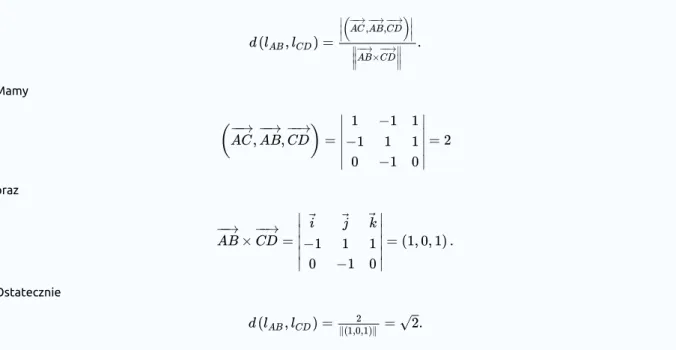Wzajemne położenie prostych i płaszczyzn

(1)

Wzajemne położenie

prostych i płaszczyzn

Autorzy:

Michał Góra

(2)

(1)

Wzajemne położenie prostych i płaszczyzn

Autor: Michał Góra

Kąty między płaszczyznami oraz prostymi

Kąt między dwiema prostymi to kąt ostry (lub prosty, gdy proste są prostopadłe) utworzony przez wektory kierunkowe tych prostych.

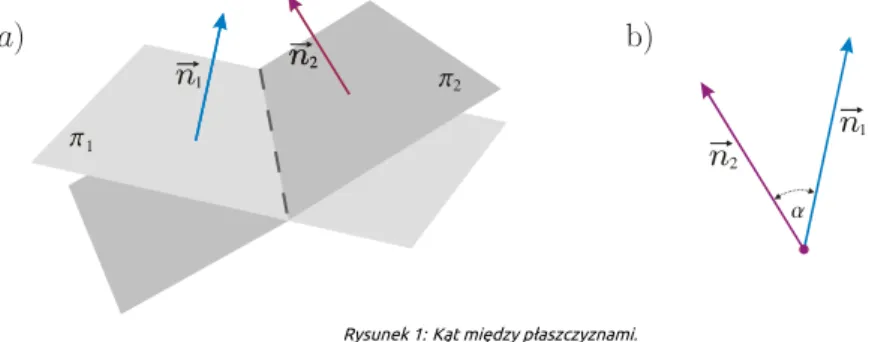
Kąt między dwiema płaszczyznami (zob. Rys. 6a) to kąt ostry (lub prosty, gdy płaszczyzny są prostopadłe) utworzony przez wektory normalne tych płaszczyzn (zob. Rys. 6b).

Rysunek 1: Kąt między płaszczyznami.

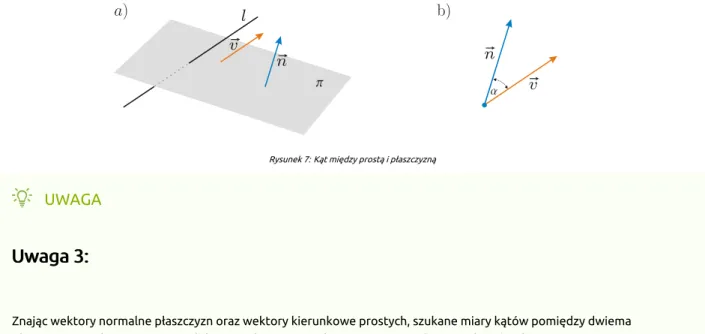
Kąt między prostą i płaszczyzną (zob. Rys. 7a), to kąt o mierze gdzie to miara kąta ostrego (lub prostego, gdy prosta i płaszczyzna są równoległe) jaki tworzą wektor kierunkowy prostej oraz wektor normalny płaszczyzny (zob. Rys. 7b).

Rysunek 2: Kąt między prostą i płaszczyzną

UWAGA

Uwaga 1:

Znając wektory normalne płaszczyzn oraz wektory kierunkowe prostych, szukane miary kątów pomiędzy dwiema płaszczyznami, dwiema prostymi lub pomiędzy prostą i płaszczyzną można łatwo wyliczyć wykorzystując stosowne własności .

Odległość punktu od płaszczyzny

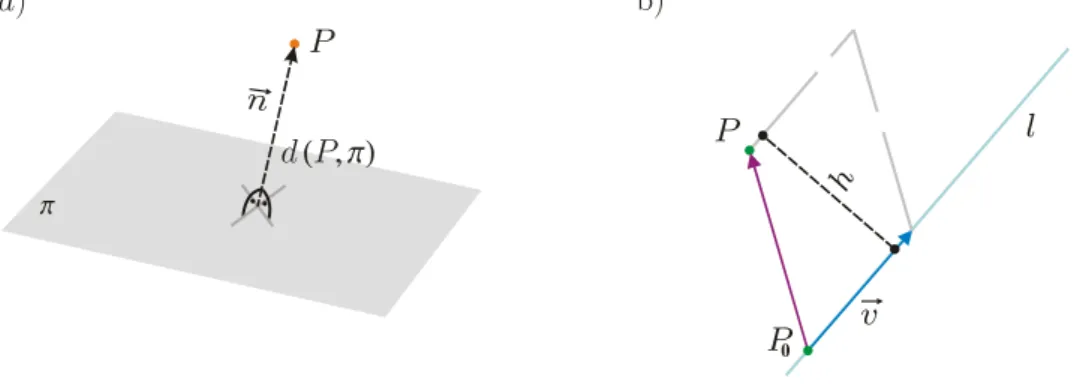
Odległość punktu od płaszczyzny wyraża się wzorem (zob. Rys. 8a)

− α,

π 2

α

P ( , , )

x

0

y

0

z

0

π : Ax + By + Cz + D = 0

d(P, π) =

|A +B +C +D|x0 y0 z0

.

+ + A2 _B2 _C2 √

(3)

(2)

Rysunek 3: Odległości: a) punktu od płaszczyzny, b) punktu od prostej.

Odległość punktu od prostej

Rozważmy punkt oraz prostą przechodzącą przez punkt i równoległą do wektora . Przypuśćmy, że punkt nie leży na prostej . Wówczas, wektory oraz tworzą równoległobok (zob. Rys. 8b). Pole tego równoległoboku, równe iloczynowi długości podstawy i wysokości , możemy obliczyć również wykorzystując stosowną własność iloczynu wektorowego:

Poszukiwana odległość punktu od prostej , równa wysokości równoległoboku rozpiętego przez wektory oraz , wyraża się więc wzorem:

Odległość prostej od płaszczyzny

Niech będzie płaszczyzną o wektorze normalnym , a prostą o wektorze kierunkowym . Aby odległość prostej od płaszczyzny była niezerowa (tj. aby prosta nie przecinała płaszczyzny) wektory i muszą być prostopadłe. W takiej sytuacji, odległość prostej od płaszczyzny jest równa odległości dowolnego punkty prostej od płaszczyzny. Aby wyznaczyć tę odległość, wybieramy dowolny punkt prostej, następnie stosujemy wzór ( 4 ).

P

l

P

0

v⃗

P

l

P

−→

−

0

P

v⃗

∥ ∥

v⃗

h

h ⋅ ∥ ∥ =

v⃗

∥

_{∥∥ P}

P

−→

−

0

×

v⃗ ∥∥∥

d(P, l)

P

l

h

v⃗

P

0

−→

−

d(P, l) =

× ∥ ∥∥ PP− →−0 v⃗ ∥∥∥ ∥∥v⃗ ∥∥

π

n⃗ l

v⃗

l

π

n⃗ v⃗

(4)

PRZYKŁAD

Przykład 1: Wyznaczanie odległości prostej od płaszczyzny

Rozważmy płaszczyznę oraz prostą

Aby wyznaczyć odległość prostej od płaszczyzny musimy sprawdzić, czy mają one wspólny punkt. Podstawiając równania prostej do równania płaszczyzny otrzymujemy równanie sprzeczne

Oznacza to, że prosta nie ma punktów wspólnych z płaszczyzną - prosta i płaszczyzna muszą więc być równoległe. Do tego samego wniosku dojdziemy licząc iloczyn skalarny wektora normalnego płaszczyzny oraz wektora kierunkowego prostej :

co oznacza, że . Odległość prostej od płaszczyzny jest więc taka sama jak odległość dowolnego punktu prostej, np. , od płaszczyzny . Na podstawie wzoru ( 4 ) mamy

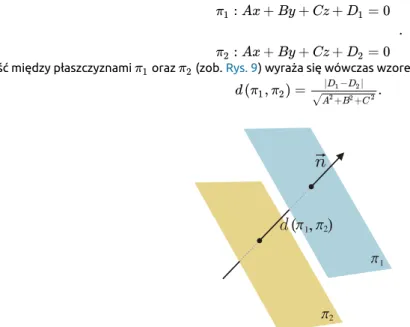
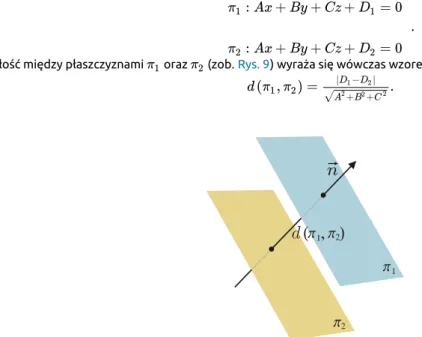
Odległość między płaszczyznami

Rozważmy dwie płaszczyzny równoległe oraz o wspólnym wektorze normalnym , tj.:

Odległość między płaszczyznami oraz (zob. Rys. 9) wyraża się wówczas wzorem

Rysunek 4: Odległość między równoległymi płaszczyznami.

π : 2x + y − 2z + 4 = 0

l :

⎧

, t ∈ R.

⎩

⎨

⎪

x = 1 + t

y = 2 − 4t

z = −t

0 = 2 (1 + t) + 2 − 4t − 2 (−t) + 4 = 8.

l

π

= (2, 1, −2)

n⃗

= (1, −4, −1)

v⃗

∘ = 2 ⋅ 1 + 1 ⋅ (−4) + (−2) ⋅ (−1) = 0,

n⃗ v⃗

⊥

n⃗ v⃗

l

π

P (1, 2, 0)

π

d(π, l) = d(π, P) =

|2⋅1+1⋅2−2⋅0+4|

= .

+ + 22 ₁2 ₍₋₂₎2 √ 8 3

π

1

π

2

n⃗

= (A, B, C)

.

: Ax + By + Cz +

= 0

π

1

D

1

: Ax + By + Cz +

= 0

π

2

D

2

π

1

π

2

d( , ) =

π

1

π

2 _√_A| − |D2_{+ +}1_BD22_C2

.

(5)

UWAGA

Uwaga 2:

Wektory normalne dwóch równoległych płaszczyzn są równoległe. Ponieważ dwa wektory równoległe oraz są proporcjonalne, tj. , dla pewnej stałej , zatem możemy przyjąć (jak w powyższym wzorze), że płaszczyzny równoległe mają wspólny wektor normalny.

PRZYKŁAD

Przykład 2: Wyznaczanie odległości między płaszczyznami

Rozważmy dwie płaszczyzny: płaszczyznę o równaniu

oraz płaszczyznę o równaniu

Wektory normalne tych płaszczyzn, równe odpowiednio oraz , łączy zależność z której wynika, że płaszczyzny oraz są równoległe. Aby wyznaczyć odległość pomiędzy nimi, musimy zapisać je w postaci kanonicznej o wspólnym wektorze normalnym. W tym celu równanie określające płaszczyznę zapiszemy w równoważnej postaci

Stąd

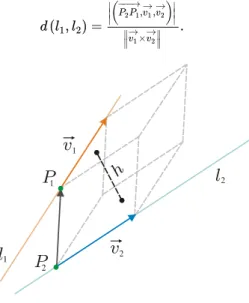
Odległość między prostymi

Niech (odpowiednio ) będzie prostą przechodzącą przez punkt (odpowiednio ) równoległą do wektora (odpowiednio ).

Proste równoległe

Przypuśćmy, że proste oraz są równoległe. Możemy wówczas przyjąć (nie tracąc ogólności), że proste te mają wspólny wektor kierunkowy, tj. . W celu wyznaczenia odległości pomiędzy prostymi oraz , wystarczy na jednej z tych prostych, powiedzmy na prostej , wybrać dowolny punkt , następnie, korzystając ze wzoru ( 5 ) na odległość punktu od prostej, wyznaczyć odległość prostej od punktu . Otrzymana wartość, równa odległości między równoległymi prostymi oraz , wyraża się wzorem:

Proste skośne

Przypuśćmy, że proste i nie są równoległe. Oznacza to, że wektory kierunkowe tych prostych, równe odpowiednio oraz

n

1

−→

_n

2

−→

= α ⋅

n

1

−→

_n

2

−→

_{α ∈ R}

π

1

3x − 6y + 2z − 4 = 0

π

2

−6x + 12y − 4z − 6 = 0.

= (3, −6, 2)

n

1

−→

_n

_{= (−6, 12, −4)}

2

−→

= −2 ⋅

n

2

−→

_n

1

−→

_π

1

π

2

π

2

3x − 6y + 2z + 3 = 0.

d( , ) =

π

1

π

2 |−4−3|

=

= 1.

+(−6 + 32 ₎2 ₂2 √ 7 49 √

l

1

l

2

P

1

P

2

v

→

1

v

2

→

l

1

l

2

=

v

1

→ v

→

2

l

1

l

2

l

2

P

2

l

1

P

2

l

1

l

2

d( , ) =

l

1

l

2

.

× ∥ ∥∥P− →−−2P1 v→∥1_∥∥ ∥ ∥v→∥1_∥

l

1

l

2

v

→

1

→

(6)

(3) , spełniają warunek

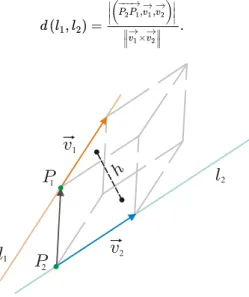
Z wektorów , oraz możemy zatem utworzyć równoległościan (zob. Rys. 10), którego objętość, równa iloczynowi pola podstawy i wysokości , można również wyrazić przy pomocy Iloczyn mieszany-Zastosowanie iloczynu mieszanego

trójki wektorów , oraz :

Poszukiwana odległość pomiędzy prostymi skośnymi oraz , równa wysokość równoległościanu rozpiętego przez wektory , oraz , wyraża się więc wzorem:

Rysunek 5: Odległość między prostymi skośnymi.

v

2

→

×

≠ .

v

1

→ v

→ 0⃗

2

v

1

→ v

→

2

− →

P

−−

2

P

1

×

∥∥v

→ v

1

→∥

2

_∥

h

v

1

→ v

→

2

− →

P

−−

2

P

1

h ⋅

∥∥v

→ v

1

×

→∥

2

_∥

= (

_{∣∣ P}

∣

− →

−−

2

P

1

, , ) .

v

→ v

1

→ ∣

2

_∣∣

d( , )

l

1

l

2

l

1

l

2

h

v

1

→ v

→

2

− →

P

−−

2

P

1

d( , ) =

l

1

l

2

.

( , , ) ∣ ∣∣ P− →−−2P1v→ v1→ ∣2 _∣∣ × ∥ ∥v→ v1 →∥2_∥

(7)

PRZYKŁAD

Przykład 3: Wyznaczanie odległości między prostymi skośnymi

Rozważmy cztery punkty . Proste oraz przechodzące

odpowiednio przez punkty oraz mają postać

Ich wektory kierunkowe oraz nie są równoległe, zatem proste te są skośne. Odległość między nimi wyznaczymy ze wzoru ( 6 ):

Mamy

oraz

Ostatecznie

Kąty między płaszczyznami oraz prostymi

Kąt między dwiema prostymi to kąt ostry (lub prosty, gdy proste są prostopadłe) utworzony przez wektory kierunkowe tych prostych.

Kąt między dwiema płaszczyznami (zob. Rys. 6a) to kąt ostry (lub prosty, gdy płaszczyzny są prostopadłe) utworzony przez wektory normalne tych płaszczyzn (zob. Rys. 6b).

Rysunek 6: Kąt między płaszczyznami.

Kąt między prostą i płaszczyzną (zob. Rys. 7a), to kąt o mierze gdzie to miara kąta ostrego (lub prostego, gdy prosta i płaszczyzna są równoległe) jaki tworzą wektor kierunkowy prostej oraz wektor normalny płaszczyzny (zob. Rys. 7b).

A (0, 1, 0) , B (−1, 2, 1) , C (1, 0, 1) , D (1, −1, 1)

l

AB

l

CD

A, B

C, D

:

(t ∈ R) oraz

:

(t ∈ R) .

l

AB

⎧

⎩

⎨

⎪

x = t

y = 1 + t

z = t

l

CD

⎧

⎩

⎨

⎪

x = 1

y = −t

z = 1

= (−1, 1, 1)

AB

−→

−

= (0, −1, 0)

CD

−→

−

d(

l

AB

,

l

CD

) =

.

( , , ) ∣ ∣∣ AC −→− AB −→− CD −→− ∣ ∣∣ × ∥ ∥∥AB −→− CD −→− ∥ ∥∥

(

AC

−→

−

,

AB

−→

−

,

−→

CD

−

) =

∣

= 2

∣

1 −1

0 −1

1 −1

1

0 ∣

∣

×

=

= (1, 0, 1) .

AB

−→

−

CD

−→

−

∣

i⃗

−1

0 j⃗

1 −1

k⃗

1

0 ∣

∣

d(

l

AB

,

l

CD

) =

_{∥(1,0,1)∥}2

=

√

2 .

− α,

π 2

α

(8)

(4)

(5)

Rysunek 7: Kąt między prostą i płaszczyzną

UWAGA

Uwaga 3:

Znając wektory normalne płaszczyzn oraz wektory kierunkowe prostych, szukane miary kątów pomiędzy dwiema płaszczyznami, dwiema prostymi lub pomiędzy prostą i płaszczyzną można łatwo wyliczyć wykorzystując stosowne własności .

Odległość punktu od płaszczyzny

Odległość punktu od płaszczyzny wyraża się wzorem (zob. Rys. 8a)

Rysunek 8: Odległości: a) punktu od płaszczyzny, b) punktu od prostej.

Odległość punktu od prostej

Rozważmy punkt oraz prostą przechodzącą przez punkt i równoległą do wektora . Przypuśćmy, że punkt nie leży na prostej . Wówczas, wektory oraz tworzą równoległobok (zob. Rys. 8b). Pole tego równoległoboku, równe iloczynowi długości podstawy i wysokości , możemy obliczyć również wykorzystując stosowną własność iloczynu wektorowego:

Poszukiwana odległość punktu od prostej , równa wysokości równoległoboku rozpiętego przez wektory oraz , wyraża się więc wzorem:

Odległość prostej od płaszczyzny

P ( , , )

x

0

y

0

z

0

π : Ax + By + Cz + D = 0

d(P, π) =

|A +B +C +D|x0 y0 z0

.

+ + A2 _B2 _C2 √

P

l

P

0

v⃗

P

l

P

−→

−

0

P

v⃗

∥ ∥

v⃗

h

h ⋅ ∥ ∥ =

v⃗

∥

_{∥∥ P}

P

−→

−

0

× .

v⃗ ∥∥∥

d(P, l)

P

l

h

v⃗

P

−→

−

0

P

d(P, l) =

×

.

∥ ∥∥ PP− →−0 v⃗ ∥∥∥ ∥∥v⃗ ∥∥

⃗ l

⃗

l

(9)

Niech będzie płaszczyzną o wektorze normalnym , a prostą o wektorze kierunkowym . Aby odległość prostej od płaszczyzny była niezerowa (tj. aby prosta nie przecinała płaszczyzny) wektory i muszą być prostopadłe. W takiej sytuacji, odległość prostej od płaszczyzny jest równa odległości dowolnego punkty prostej od płaszczyzny. Aby wyznaczyć tę odległość, wybieramy dowolny punkt prostej, następnie stosujemy wzór ( 4 ).

PRZYKŁAD

Przykład 4: Wyznaczanie odległości prostej od płaszczyzny

Rozważmy płaszczyznę oraz prostą

Aby wyznaczyć odległość prostej od płaszczyzny musimy sprawdzić, czy mają one wspólny punkt. Podstawiając równania prostej do równania płaszczyzny otrzymujemy równanie sprzeczne

Oznacza to, że prosta nie ma punktów wspólnych z płaszczyzną - prosta i płaszczyzna muszą więc być równoległe. Do tego samego wniosku dojdziemy licząc iloczyn skalarny wektora normalnego płaszczyzny oraz wektora kierunkowego prostej :

co oznacza, że . Odległość prostej od płaszczyzny jest więc taka sama jak odległość dowolnego punktu prostej, np. , od płaszczyzny . Na podstawie wzoru ( 4 ) mamy

Odległość między płaszczyznami

Rozważmy dwie płaszczyzny równoległe oraz o wspólnym wektorze normalnym , tj.:

Odległość między płaszczyznami oraz (zob. Rys. 9) wyraża się wówczas wzorem

Rysunek 9: Odległość między równoległymi płaszczyznami.

π

n⃗ l

v⃗

l

π

n⃗ v⃗

π : 2x + y − 2z + 4 = 0

l :

⎧

, t ∈ R.

\n

⎩

⎨

⎪

x = 1 + t

y = 2 − 4t

z = −t

0 = 2 (1 + t) + 2 − 4t − 2 (−t) + 4 = 8.

l

π

= (2, 1, −2)

n⃗

= (1, −4, −1)

v⃗

∘ = 2 ⋅ 1 + 1 ⋅ (−4) + (−2) ⋅ (−1) = 0,

n⃗ v⃗

⊥

n⃗ v⃗

l

π

P (1, 2, 0)

π

d(π, l) = d(π, P) =

|2⋅1+1⋅2−2⋅0+4|

= .

+ + 22 ₁2 ₍₋₂₎2 √ 8 3

π

1

π

2

n⃗

= (A, B, C)

.

: Ax + By + Cz +

= 0

π

1

D

1

: Ax + By + Cz +

= 0

π

2

D

2

π

1

π

2

d( , ) =

π

1

π

2 _√_A| − |D2_{+ +}1_BD22_C2

.

(10)

UWAGA

Uwaga 4:

Wektory normalne dwóch równoległych płaszczyzn są równoległe. Ponieważ dwa wektory równoległe oraz są proporcjonalne, tj. , dla pewnej stałej , zatem możemy przyjąć (jak w powyższym wzorze), że płaszczyzny równoległe mają wspólny wektor normalny.

PRZYKŁAD

Przykład 5: Wyznaczanie odległości między płaszczyznami

Rozważmy dwie płaszczyzny: płaszczyznę o równaniu

oraz płaszczyznę o równaniu

Wektory normalne tych płaszczyzn, równe odpowiednio oraz , łączy zależność , z której wynika, że płaszczyzny oraz są równoległe. Aby wyznaczyć odległość pomiędzy nimi, musimy zapisać je w postaci kanonicznej o wspólnym wektorze normalnym. W tym celu równanie określające płaszczyznę zapiszemy w równoważnej postaci

Stąd

Odległość między prostymi

Niech (odpowiednio ) będzie prostą przechodzącą przez punkt (odpowiednio ) równoległą do wektora (odpowiednio ).

Proste równoległe

Przypuśćmy, że proste oraz są równoległe. Możemy wówczas przyjąć (nie tracąc ogólności), że proste te mają wspólny wektor kierunkowy, tj. . W celu wyznaczenia odległości pomiędzy prostymi oraz , wystarczy na jednej z tych prostych, powiedzmy na prostej , wybrać dowolny punkt , następnie, korzystając ze wzoru ( 5 ) na odległość punktu od prostej, wyznaczyć odległość prostej od punktu . Otrzymana wartość, równa odległości między równoległymi prostymi oraz , wyraża się wzorem:

Proste skośne

Przypuśćmy, że proste i nie są równoległe. Oznacza to, że wektory kierunkowe tych prostych, równe odpowiednio oraz , spełniają warunek

n

1

−→

_n

2

−→

= α ⋅

n

1

−→

_n

2

−→

_{α ∈ R}

π

1

3x − 6y + 2z − 4 = 0

π

2

−6x + 12y − 4z − 6 = 0.

= (3, −6, 2)

n

1

−→

_n

_{= (−6, 12, −4)}

2

−→

= −2 ⋅

n

2

−→

_n

1

−→

_π

1

π

2

π

2

3x − 6y + 2z + 3 = 0.

d( , ) =

π

1

π

2 |−4−3|

=

= 1.

+(−6 + 32 ₎2 ₂2 √ 7 49 √

l

1

l

2

P

1

P

2

v

→

1

v

2

→

l

1

l

2

=

v

1

→ v

→

2

l

1

l

2

l

2

P

2

l

1

P

2

l

1

l

2

d( , ) =

l

1

l

2

.

× ∥ ∥∥P− →−−2P1 v→∥1_∥∥ ∥ ∥v→∥1_∥

l

1

l

2

v

→

1

v

2

→

×

≠

→ →

_⃗

(11)

(6) .

Z wektorów , oraz

możemy zatem utworzyć równoległościan (zob. Rys. 10), którego objętość, równa iloczynowi pola podstawy i wysokości , można również wyrazić przy pomocy Iloczyn mieszany-Zastosowanie iloczynu mieszanego trójki wektorów , oraz

Poszukiwana odległość pomiędzy prostymi skośnymi oraz , równa wysokość równoległościanu rozpiętego przez wektory , oraz , wyraża się więc wzorem:

Rysunek 10: Odległość między prostymi skośnymi.

×

≠

v

1

→ v

→ 0⃗

2

v

1

→ v

→

2

P

2

P

1

− →

−−

_×

∥∥v

→ v

1

→∥

2

_∥

h

v

→ v

1

→

2

P

2

P

1

− →

−−

h ⋅

∥∥v

→ v

1

×

→∥

2

_∥

= (

_{∣∣ P}

∣

− →

−−

2

P

1

, , ) .

v

→ v

1

→ ∣

2

_∣∣

d( , )

l

1

l

2

l

1

l

2

h

v

1

→ v

→

2

− →

P

−−

2

P

1

d( , ) =

l

1

l

2

.

( , , ) ∣ ∣∣ P− →−−2P1v→ v1→ ∣2 _∣∣ × ∥ ∥v→ v1 →∥2_∥

(12)

PRZYKŁAD

Przykład 6: Wyznaczanie odległości między prostymi skośnymi

Rozważmy cztery punkty , , , . Proste oraz przechodzące odpowiednio przez punkty oraz mają postać

Ich wektory kierunkowe oraz nie są równoległe, zatem proste te są skośne. Odległość między nimi wyznaczymy ze wzoru ( 6 ):

Mamy

oraz

Ostatecznie

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-16 01:12:14

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=06d42eef0a1f45ef2c2601f26dd34f3d

Autor: Michał Góra

A (0, 1, 0) B (−1, 2, 1) C (1, 0, 1) D (1, −1, 1)

l

AB

l

CD

A, B

C, D

:

(t ∈ R) oraz

:

(t ∈ R) .

l

AB

⎧

⎩

⎨

⎪

x = t

y = 1 + t

z = t

l

CD

⎧

⎩

⎨

⎪

x = 1

y = −t

z = 1

= (−1, 1, 1)

AB

−→

−

= (0, −1, 0)

CD

−→

−

d(

l

AB

,

l

CD

) =

.

( , , ) ∣ ∣∣ AC −→− AB −→− CD −→− ∣ ∣∣ × ∥ ∥∥AB −→− CD −→− ∥ ∥∥