Własności funkcji ciągłych

(1)

Własności funkcji ciągłych

Autorzy:

Anna Barbaszewska-Wiśniowska

(2)

Własności funkcji ciągłych

Autor: Anna Barbaszewska-Wiśniowska

TWIERDZENIE

Twierdzenie 1: o działaniach arytmetycznych na funkcjach ciągłych

Jeżeli funkcje określone w zbiorze są ciągłe w punkcie , to funkcje (gdy ), są ciągłe w punkcie .

TWIERDZENIE

Twierdzenie 2: o ciągłości funkcji złożonej

Jeżeli funkcja jest ciągła w punkcie i funkcja jest ciągła w punkcie oraz złożenie ma sens, wówczas funkcja złożona jest ciągła w punkcie .

TWIERDZENIE

Twierdzenie 3: o ciągłości funkcji odwrotnej

Jeżeli funkcja jest ciągła i ściśle monotoniczna w przedziale , to funkcja odwrotna jest ciągła w przedziale , w szczególności:

jeśli funkcja jest ciągła i rosnąca w przedziale , to funkcja odwrotna jest ciągła i rosnąca w przedziale ,

jeśli funkcja jest ciągła i malejąca w przedziale , to funkcja odwrotna jest ciągła i malejąca w przedziale .

PRZYKŁAD

Przykład 1:

Funkcja jest ciągła i rosnąca w przedziale . Funkcja do niej odwrotna jest

ciągła i rosnąca w przedziale .

=sin x 1 -π/2 -1 π/2 -π/2 π/2 [-π/2,π/2] =arcsin x

f i g

A ⊂ R

x

0

∈ A

f + g, f − g, f ⋅ g,

f_g

g( ) = 0

x

0

/

x

0

f

x

0

g

y

0

= f( )

x

0

g ∘ f

x

0

f

J

f

−1

_f(J)

f

[a, b]

f

−1

[f(a), f(b)]

f

[a, b]

f

−1

[f(b), f(a)]

f(x) = sin x

[[− , ]π 2 π2

[− , ]

π 2 π2

f

−1

(x) = arcsinx

[f(− ), f( )] = [−1, 1]

π 2 π2

(3)

Rysunek 1: Ilustracja faktu, że funkcja odwrotna do funkcji ciągłej i rosnącej w przedziale jest również funkcją ciągłą i rosnącą.

PRZYKŁAD

Przykład 2:

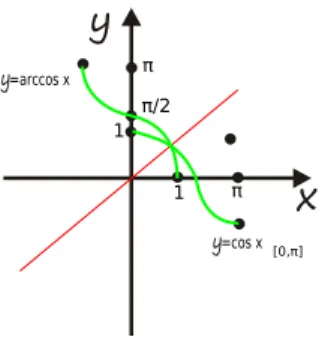
Funkcja jest ciągła i malejąca w przedziale . Funkcja do niej odwrotna jest ciągła

i malejąca w przedziale . =cos x 1 π/2 [0,π] =arccos x π π 1

Rysunek 2: Ilustracja faktu, że funkcja odwrotna do funkcji ciągłej i malejącej w przedziale jest również funkcją ciągłą i malejącą.

UWAGA

Uwaga 1:

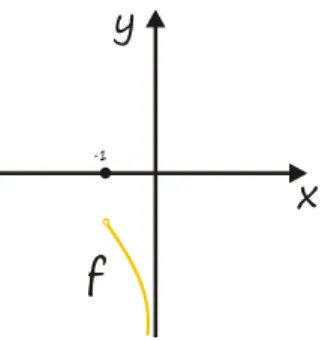
W twierdzeniu o ciągłości funkcji odwrotnej istotne jest założenie o przedziale. Funkcja odwrotna do funkcji ciągłej w dowolnym zbiorze nie musi być ciągła. Na przykład funkcja dana wzorem

jest ciągła w zbiorze , gdyż jest ona ciągła w każdym punkcie tego zbioru, natomiast funkcja do niej odwrotna

nie jest ciągła, gdyż nie jest ona ciągła w punkcie (nie istnieje granica funkcji w tym punkcie, bo ).

Rysunek 3: Funkcja ciągła w zbiorze , do której odwrotna nie jest ciągła.

f(x) = cos x

[[0,π]

[0, π]

f

−1

(x) = arccosx

[f(π), f(0)] = [−1, 1]

f(x) = { x

_{x − 1}

dla x ∈ [0, 1)

_{dla x ∈ [2, 3]}

A = [0, 1) ∪ [2, 3]

f(x) = { x

x + 1

dla x ∈ [0, 1)

dla x ∈ [1, 2]

= 1

x

0

(x) = 1 =

(x) = 2

lim

x→−1−

f

−1

/ lim

_x→1+

f

−1 f A = [0, 1) ∪ [2, 3] f−1

(4)

TWIERDZENIE

Twierdzenie 4: o monotoniczności funkcji ciągłej i różnowartościowej

Niech funkcja będzie ciągła w przedziale . Wówczas jest różnowartościowa wtedy i tylko wtedy, gdy jest ściśle monotoniczna w tym przedziale.

TWIERDZENIE

Twierdzenie 5:

Twierdzenie 5: Weierstrassa (o osiąganiu kresów przez funkcje ciągłą w

Weierstrassa (o osiąganiu kresów przez funkcje ciągłą w

przedziale domkniętym)

Jeżeli funkcja jest ciągła w przedziale domkniętym , to jest w tym przedziale ograniczona i osiąga swoje kresy tzn. istnieją takie punkty w przedziale , że

. f( y=M a c2 b=c1 y=-M 2 c )= sup f(x) f(c )= inf f(x)1 _xϵ[a,b] xϵ[a,b]

Rysunek 4: Ilustracja twierdzenia Weierstrassa.

UWAGA

Uwaga 2:

W twierdzeniu Weierstrassa ważne jest, by funkcja była ciągła w przedziale domkniętym. Nie wystarcza ciągłość w przedziale otwartym, bo np. funkcja ciągła w przedziale nie osiąga ani kresu dolnego ani górnego i nie jest ograniczona (bo nie jest ograniczona z dołu).

Rysunek 5: Funkcja ciągła w przedziale otwartym nieosiągająca kresów i nieograniczona.

f

[a, b]

f

[a, b]

,

c

1

c

2

[a, b]

f( ) =

c

1

inf

f(x), f( ) =

f(x)

x∈[a,b]

c

2 _x∈[a,b]

sup

f(x) =

1

(5)

TWIERDZENIE

Twierdzenie 6: Własność Darboux (przyjmowanie wartości pośrednich przez

funkcję ciągłą w przedziale)

Jeżeli funkcja jest ciągła w przedziale oraz i leży pomiędzy , to istnieje taki punkt

pośredni , że .

UWAGA

Uwaga 3:

Własność Darboux orzeka, że funkcja ciągła w przedziale przyjmuje wszystkie wartości pośrednie między , więc jej wykres nie może się przerywać w tym przedziale.

a b c f(b) f(a) a b c f(a) f(b) ξ ξ ξ1 2 3

Rysunek 6: Ilustracja własności Darboux.

UWAGA

Uwaga 4: O istnieniu punktów pośrednich

Z własności Darboux wynika, że przy stosownych założeniach o funkcji dla danego (z twierdzenia 6) istnieje przynajmniej jeden punkt . Może być ich więcej, gdy funkcja nie jest różnowartościowa tak jak na drugim rysunku w poprzednim przykładzie.

TWIERDZENIE

Twierdzenie 7: Wniosek z własności Darboux o znajdowaniu przybliżonych miejsc

zerowych funkcji

Jeżeli funkcja jest ciągła w przedziale , to istnieje punkt taki, że .

f

[a, b]

f(a) = f(b)

/

c

f(a) i f(b)

ξ ∈ (a, b)

f(ξ) = c

[a, b]

f(a) i f(b)

c

ξ

(6)

UWAGA

Uwaga 5:

Założenie oznacza, że wartości funkcji na końcach przedziału maja różne znaki, leżą po różnych stronach osi , a jako że wykres (zgodnie z twierdzeniem Darboux) nie może się „przerywać”, więc musi przeciąć, przynajmniej raz oś . a b f(b) ξ ξ ξ1 _f(a) 2 3

Rysunek 7: Ilustracja wniosku z własności Darboux o miejscach zerowych funkcji.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-16 01:14:30

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=fe5e2fab2ccd8c9b4e359800073b47a2

Autor: Anna Barbaszewska-Wiśniowska