Twierdzenia pozwalające wyliczać granice ciągów

(1)

Twierdzenia pozwalające

wyliczać granice ciągów

Autorzy:

Katarzyna Czyżewska

(2)

Twierdzenie 1:

Twierdzenie 1: o działaniach arytmetycznych na ciągach zbieżnych

o działaniach arytmetycznych na ciągach zbieżnych

Jeżeli i , to

PRZYKŁAD

Przykład 1:

Oblicz granicę Rozwiązanie:

Korzystamy z twierdzenia o działaniach arytmetycznych na ciągach zbieżnych, otrzymując

PRZYKŁAD

Przykład 2:

Zauważmy, że nie możemy od razu skorzystać z twierdzenia o działaniach arytmetycznych na ciągach zbieżnych, bo ciągi w liczniku i mianowniku są rozbieżne do . Wykonamy najpierw przekształcenie algebraiczne, które pozwoli uzyskać ciągi zbieżne

= a

limn→∞

a

n

limn→∞

b

n

= b

( + ) = a + b,

limn→∞

a

n

b

n

(c ⋅ ) = c ⋅ a dla dowolnego c ∈ R,

limn→∞

a

n

( ⋅ ) = a ⋅ b,

lim

n→∞

a

n

b

n

= , b ∈ R ∖ {0}.

limn→∞

an bn a b

( + − 5)

limn→∞

3 n2 _n2

( + − 5) = [3 ⋅ 0 + 2 ⋅ 0 − 5] = [0 − 5] = −5

limn→∞

3 n2 _n2

limn→∞

(3n+1)(−2n+4)_1−3n−2n2

−∞

=

= [

] = 3

limn→∞

(3n+1)(−2n+4)_1−3n−2n2

limn→∞

(3+ )(−2+ ) n2 1 n n4 ( − −2) n2 1 n2 3 n (3+0)(−2+0) 0−0−2

(3)

PRZYKŁAD

Przykład 3:

Obliczmy Rozwiązanie:

W liczniku i w mianowniku ułamka, który jest wyrazem naszego ciągu mamy ciągi rozbieżne do , czyli wykonujemy przekształcenie algebraiczne pozwalające uzyskać ciągi zbieżne

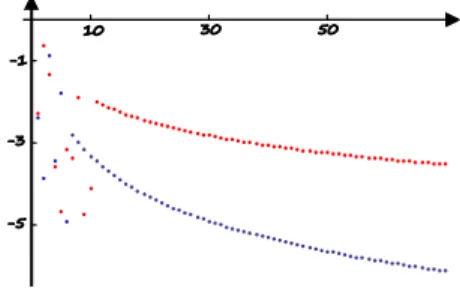
Rysunek 1: Interpretacja twierdzenia o dwóch ciągach rozbieżnych do

Rys. 1 przedstawia na jednym wykresie dwa ciągi, z których jeden ma od pewnego miejsca wyrazy większe od drugiego. Na pierwszym wykresie ciąg o wyrazach mniejszych (czerwony) jest rozbieżny do i na podstawia twierdzenia o zachowaniu nierówności w granicy możemy wnioskować, że ciąg o wyrazach większych (niebieski) też musi być rozbieżny do .

Rysunek 2: Interpretacja geometryczna twierdzenia o dwóch ciągach rozbieżnych do

Na Rys. 2 przedstawiony jest ciąg o wyrazach większych (czerwony), który jest rozbieżny do i stąd wnioskujemy, że ciąg o wyrazach mniejszych (niebieski) tez musi być rozbieżny do .

limn→∞

_{(4n−2) 8 +2n}√327 +3 +2n6_√_nn22

+∞

=

= [

] =

limn→∞

_{(4n−2) 8 +2n}√327 +3 +2n6_√_nn22

limn→∞

(27+ + ) n6 3 n4 2 n6 √3 n(4− )2 n √n2(8+ )n2

limn→∞

n2 27+ + 3 n4 2 n6 √3 (4− ) n2 2 n √8+2n 27+0+0 √3 (4−0) 8+0√ 8 2√3 +∞

+∞

−∞

(4)

Jeżeli oraz od pewnego miejsca pomiędzy wyrazami dwóch ciągów zachodzą nierówności , to lub

Jeżeli oraz od pewnego miejsca pomiędzy wyrazami dwóch ciągów zachodzą nierówności , to .

PRZYKŁAD

Przykład 4:

Skorzystamy z twierdzenia o dwóch ciągach i wykorzystamy ograniczenie dla funkcji sinus prawdziwą dla wszystkich naturalnych.

Ponieważ ciąg o wyrazach większych jest rozbieżny do , zatem

PRZYKŁAD

Przykład 5:

Skorzystamy z twierdzenia o dwóch ciągach i będziemy wyraz naszego ciągu ograniczać od dołu. Zauważamy, że każdy wyraz ciągu jest sumą ułamków postaci i składników sumy jest więcej im większe jest , czyli w -tym wyrazie ciągu jest dokładnie składników. Aby ograniczyć tę sumę od dołu wybieramy składnik najmniejszy i mnożymy go przez liczbę składników otrzymując

Ponieważ ciąg o wyrazach mniejszych jest rozbieżny do , więc .

= +∞

limn→∞

a

n

a

n

≤

b

n

= +∞

limn→∞

b

n

= −∞

limn→∞

b

n

a

n

≤

b

n

= −∞

limn→∞

a

n

(3 sin n − 5) ⋅

limn→∞

n

3

sin n ≤ 1

n

(3 sin n − 5) ⋅

n

3

≤ (3 ⋅ 1 − 5) ⋅

_n

3

= −2 ≤ −n

_n

3 n→∞

_⟶

−∞

limn→∞

(3 sin n − 5) ⋅

n

3

= −∞

(

+

+ ⋯ +

)

limn→∞

1 1 √ √12 √1n 1 k √

n

+∞

n→∞

⟵

√

n

=

1

⋅ n ≤

+

+ ⋯ +

n √ √11 √12 √1n

+∞

limn→∞

(

1

+

+ ⋯ +

) = +∞

1 √ √12 √1n

(5)

PRZYKŁAD

Przykład 6:

Oblicz granicę .

Rozwiązanie:

Skorzystamy z twierdzenia i ograniczenia dla funkcji cosinus dla wszystkich naturalnych. Otrzymujemy ograniczenie od dołu dla wyrazów naszego ciągu

Ponieważ zachodzi kolejne ograniczenie

oraz ciąg o wyrazach mniejszych jest rozbieżny do , to .

PRZYKŁAD

Przykład 7:

Oblicz granicę .

Rozwiązanie:

Skorzystamy z twierdzenia o dwóch ciągach i zauważamy, że . Otrzymujemy ograniczenie od góry wyrazu naszego ciągu

Ponieważ ciąg o wyrazach większych jest rozbieżny do , to .

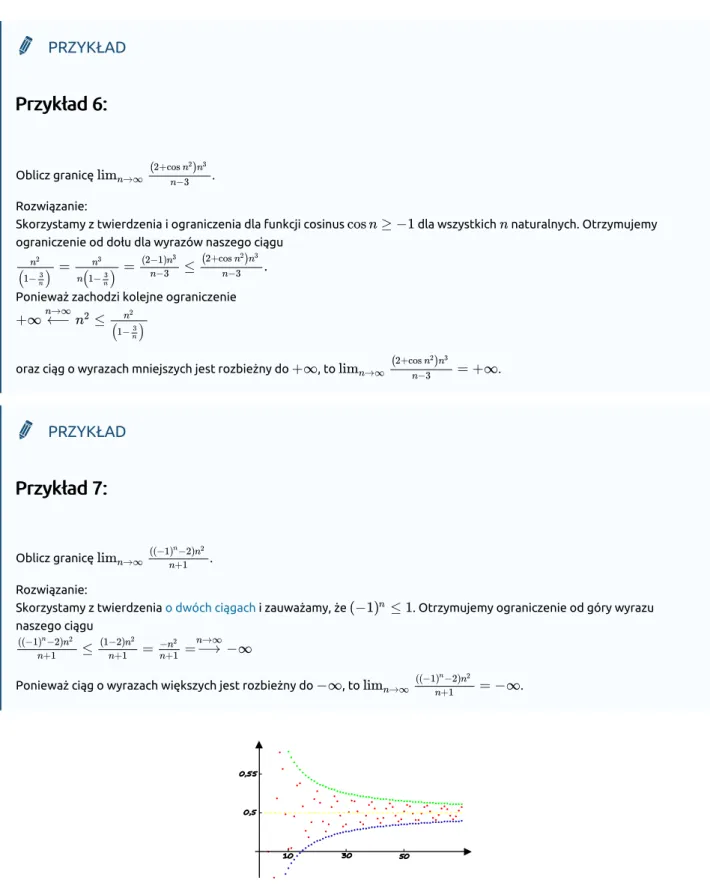
Rysunek 3: Interpretacja geometryczna twierdzenia o trzech ciągach

Rys. 3 przedstawia na jednym wykresie trzy ciągi, z których jeden (czerwony) ma wyrazy od pewnego miejsca leżące pomiędzy wyrazami dwóch innych ciągów (niebieskiego i zielonego), przy czym ciągi o wyrazach skrajnych są zbieżne do tej samej granicy właściwej . Ponieważ prawie wszystkie wyrazy ciągów skrajnych leżą w przedziale , a wyrazy ciągu środkowego leżą pomiędzy wyrazami ciągów skrajnych, to z konieczności w przedziale leża prawie wszystkie wyrazy ciągu środkowego, czyli ma on taką sama granicę .

limn→∞

(2+cos )_n−3n2n3

cos n ≥ −1

n

=

≤

.

n2 (1− )3 n n3 n(1− )3 n (2−1)n3 n−3 (2+cos ) n2_n3 n−3

+∞

n→∞

⟵

n

2

≤

n2 (1− )3 n

+∞

limn→∞

(2+cos )_n−3n2n3

= +∞

limn→∞

((−1 −2)_n+1)n n2

(−1 ≤ 1

)

n

≤

=

−∞

((−1 −2))n _n2 n+1 (1−2)n 2 n+1 −n 2 n+1

⟶

n→∞

−∞

limn→∞

((−1 −2)_n+1)n n2

= −∞

g

(g − ϵ, g + ϵ)

g

(6)

Jeżeli oraz od pewnego miejsca zachodzi nierównośc pomiędzy wyrazami trzech ciągów , to ciąg jest zbieżny i .

PRZYKŁAD

Przykład 8:

Skorzystamy z twierdzenia o trzech ciągach szacując wyraz naszego ciągu od dołu i od góry tak, aby otrzymać ciągi o tej samej granicy i wykorzystujemy znane ograniczenia funkcji sinus i cosinus i , które są prawdziwe dla każdego naturalnego

Zatem wnioskujemy, że

PRZYKŁAD

Przykład 9:

Skorzystamy z twierdzenia o trzech ciągach i szacowania sumy od góry przez największy składnik pomnożony przez liczbę składników, a od dołu przez najmniejszy składnik pomnożony przez liczbę składników.

Zauważmy, że oraz

Ponieważ skrajne ciągi mają tę samą granicę, to .

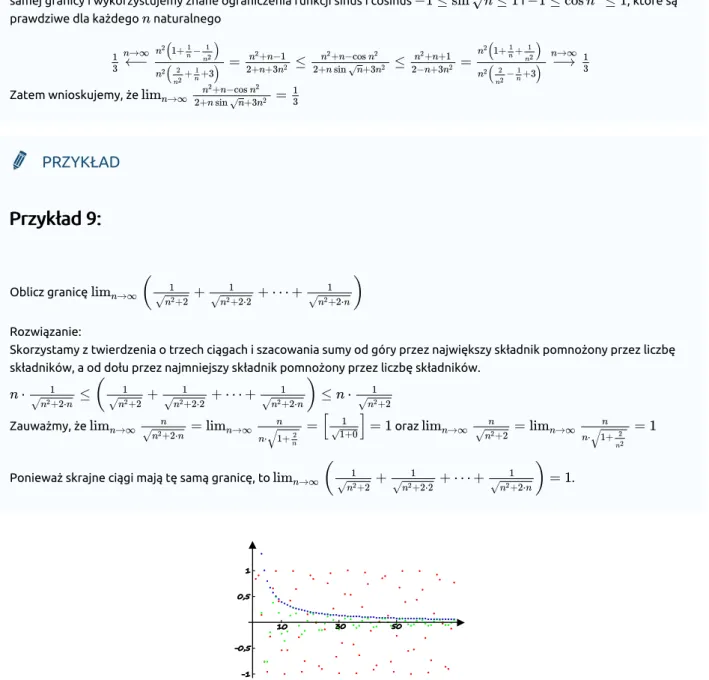
Rysunek 4: Interpretacja geometryczna granicy iloczynu ciągów, z których jeden jest zbieżny do zera, a drugi jest ograniczony

= g =

limn→∞

a

n

limn→∞

c

n

≤ ≤

a

n

b

n

c

n

( )

b

n

limn→∞

b

n

= g

limn→∞

n2+n−cos_n2 2+n sin√n+3n2

−1 ≤ sin

√

n

≤ 1

−1 ≤ cos

n

2

≤ 1

n

=

≤

=

1 3

⟵

n→∞ n2(1+ − )1 n _n21 ( + +3) n2 2 n2 1 n +n−1 n2 2+n+3n2 n+n−cos 2 _n2 2+n sin√n+3n2 n+n+1 2 2−n+3n2 (1+ + ) n2 1 n _n21 ( − +3) n2 2 n2 1 n

⟶

n→∞ 1 3

=

limn→∞

n2+n−cos_n2 2+n sin√n+3n2 1₃

(

+

+ ⋯ +

)

limn→∞

1 +2 n2 √ _√n21+2⋅2 _√_n21_+2⋅n

n ⋅

1

≤ (

+

+ ⋯ +

) ≤ n ⋅

+2⋅n n2 √ _√n12+2 _√_n21_+2⋅2 _√_n21_+2⋅n _√_n12₊₂

=

= [

] = 1

limn→∞

n +2⋅n n2 √

limn→∞

_{n⋅ 1+}n 2 n √ 1 1+0 √

limn→∞

_√nn2+2

=

limn→∞

_{n⋅ 1+}n 2

= 1

n2 √

(

+

+ ⋯ +

) = 1

limn→∞

1 +2 n2 √ _√n21+2⋅2 _√_n21_+2⋅n

(7)

Rys. 4 przedstawia wykres ciągu zbieżnego do zera (niebieski) oraz wykres ciągu ograniczonego (czerwony) i wykres ciągu, którego każdy wyraz jest iloczynem wyrazów poprzednich ciągów (zielony). Ponieważ prawie wszystkie wyrazy ciągu zbieżnego do zera leżą w przedziale i wszystkie wyrazy ciągu ograniczonego lezą w przedziale , to prawie wszystkie wyrazy iloczynu tych ciągów leżą w przedziale . Z dowolności liczby otrzymujemy, że liczba może też być dowolnie mała, czyli liczba zero jest granicą iloczynu wyjściowych ciągów.

TWIERDZENIE

Twierdzenie 4:

Twierdzenie 4: o iloczynie ciągu zbieżnego do zera i ciągu ograniczonego

o iloczynie ciągu zbieżnego do zera i ciągu ograniczonego

Jeżeli i ciąg jest ograniczony, to

PRZYKŁAD

Przykład 10:

Obliczmy .

Rozwiązanie:

skorzystamy z twierdzenia o iloczynie ciągu zbieżnego do zera i ciągu ograniczonego otrzymując

Zatem .

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 05:05:58

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=67ad6612412f6f8a8571264e920bf445