CHARAKTERYSTYKI CZASOWE UKŁADÓW DYNAMICZNYCH
Zadanie 1 Charakterystyki czasowe układów.
Problem:Wyznaczyć odpowiedz skokową i impulsową całkującego z inercją
s
sT
k
s
G
)
1
(
)
(
+
=
(1)s
sT
k
s
X
s
Y
s
G
)
1
(
)
(
)
(
)
(
+
=
=
(2)s
1
;
1
=
= T
k
(3) Odpowiedź skokową wyznacza się ze wzoru:( )
t
L
1{
G
( )
s
X
(
s
)
}
h
=
−( )
( )
=
−s
s
G
L
t
h
1 gdzie:s
X
(
)
=
1
jest skokiem jednostkowym Odpowiedź skokowa
+
=
−)
1
(
1
)
(
1sT
s
k
s
L
t
h
(4) + = − ) 1 ( ) ( 1 2 sT s k L t h (5)Rozkładamy na ułamki proste
)
1
(
1
)
1
(
2 2 2+
=
+
+
Ts
+
⋅
s
Ts
+
C
s
B
s
A
Ts
s
k
(6) (7) 2)
1
(
)
1
(
*
Ts
Bs
Ts
Cs
A
k
=
+
+
+
+
(8)A
B
AT
s
C
B
s
k
=
2(
+
)
+
(
+
)
+
(9) = = + = + k A B AT C B 0 0 (10) = − = − = k A AT B B C
+
+
−
=
−1
)
(
1 2Ts
kT
s
kT
s
k
L
t
h
(11) T tkTe
kT
kt
t
h
(
)
=
−
+
− (12)
−
−
=
−T te
T
t
k
t
h
(
)
1
(13)Odpowiedź impulsowa:
+
=
−)
1
(
)
(
1sT
s
k
L
t
g
(14)Rozkładamy na ułamki proste
)
1
(
1
)
1
(
+
=
+
Ts
+
⋅
s
Ts
+
B
s
A
Ts
s
k
(15)g
(16)Bs
Ts
A
k
=
(
+
1
)
+
g =LA
B
AT
s
k
=
(
+
)
+
(17) (18)
+
=
=
B
AT
k
A
0
(19)
=
−
=
B
kT
k
A
Odpowiedź impulsowa wyznacza się ze wzoru:( )
{
*
(
)
}
)
(
t
=
L
−1G
s
X
s
( )
{
}
( )
{
G s}
t s G L t g 1 1 ) ( 1 * ) ( − − = gdzie:1
)
(
s
=
X
jest transformatą impulsu Diraca (x(t)=δ(t))1
)
1
(
+
−
+
=
+
Ts
kT
s
k
Ts
s
k
(20)
+
−
+
=
−1
)
(
1Ts
AT
s
k
L
t
g
(21) T tkTe
k
t
g
(
)
=
−
− (22))
1
(
)
(
T tTe
k
t
g
=
−
− (23) Odpowiedź liniowa
+
=
− 2 11
)
1
(
)
(
s
sT
s
k
L
t
y
(24) + = − ) 1 ( ) ( 1 3 sT s k L t y (25)Rozkładamy na ułamki proste
)
1
(
1
)
1
(
3 2 3 3+
=
+
+
+
Ts
+
⋅
s
Ts
+
D
s
C
s
B
s
A
Ts
s
k
(26) (27)A
s
B
AT
s
C
BT
s
CT
D
k
=
(
+
)
3+
(
+
)
2+
(
+
)
+
Odpowiedz liniową oblicza się ze wzoru:
{
(
)
(
)
}
)
(
t
L
1G
s
X
s
y
=
−( )
=
− 2 1)
(
s
s
aG
L
t
y
gdzie:„a” jest to wartość stała, prędkość narastania sygnału
a
s
s
X
(
)
=
1
2*
(28)
=
+
=
+
=
+
=
0
0
0
CT
D
c
BT
B
AT
k
A
(28)
−
=
⇒
=
+
=
⇒
=
+
−
−
=
⇒
=
+
=
2 20
0
0
kT
D
kT
D
kT
C
C
kT
kT
B
B
kT
k
A
1
)
1
(
2 2 3 3+
=
−
+
−
Ts
+
kT
s
kT
s
kT
s
kT
Ts
s
k
(30) + − + − = − 1 ) ( 1 3 2 2 Ts kT s kT s kT s kT L t y (31)
−
+
−
=
−T te
T
T
t
T
t
k
t
y
2*
22
)
(
(32)
−
+
−
=
−T te
T
T
t
T
t
kT
t
y
1
2
)
(
2 2 2 (33)Rys. 1 Odpowiedz skokowa.
Rys. 3 Odpowiedź liniowa
Zadanie 2 Charakterystyki czasowe układów.
Problem:Wyznaczyć odpowiedz skokową i impulsową obiektu różniczkowego z inercją (przy wyznaczeniu
odpowiedzi impulsowej rząd względny funkcji wymiernej , której orginał ma być wyznaczony wynosi zero , w związku z czym nie można bezpośrednio zastosować wzoru na transformatę odwrotną).
sT
sk
s
G
+
=
1
)
(
(1)sT
sk
s
X
s
Y
s
G
+
=
=
1
)
(
)
(
)
(
(2)1
;
1
=
= T
k
(3) Odpowiedź skokowa
+
=
−sT
sk
s
L
t
h
1
1
)
(
1 (4)L
+
=
−sT
k
L
t
h
1
)
(
1 (5) Odpowiedź skokową wyznacza się ze wzoru:( )
t
L
1{
G
( )
s
*
X
(
s
)
}
h
=
−( )
( )
=
−s
s
G
t
h
1 gdzie:s
s
X
(
)
=
1
jest skokiem jednostkowym
+
=
−s
T
T
k
L
t
h
1
)
(
1 (6) T te
T
k
t
h
(
)
=
− (7)Odpowiedź impulsowa
+
=
−sT
sk
L
t
g
1
)
(
1 (8) + − + = − sT T k T k T k T L t g 1 ) ( 1 (9) g =L + − + + = − sT T k sT sT T k L t g 1 1 1 ) ( 1 (10) + − = − sT T k T k L t g 1 ) ( 1 (11) T te
T
k
t
T
k
t
g
(
)
=
δ
(
)
−
− (12))
)
(
(
)
(
T te
t
T
k
t
g
=
δ
−
− (13) Odpowiedź liniowa
+
=
− 2 1*
1
)
1
(
)
(
s
sT
sk
L
t
y
(14)
+
=
−)
1
(
)
(
1sT
s
k
L
t
y
(15) + = − ) 1 ( ) ( 1 s T sT k L t y (16))
(t
δ
- impuls Diraca natomiast{ }
(
)
1t
L
− Tk=
δ
{ }
T te
L
− +sT=
− 11 1Odpowiedz liniowa oblicza się ze wzoru
gdzie:
„a” jest to wartość stała, jest to prędkość narastania sygnału linowego
a
s
s
X
(
)
=
1
2 :{
(
)
(
)
}
)
(
t
L
1G
s
X
s
y
=
−( )
=
− 2 1)
(
s
s
aG
L
t
y
Odpowiedź impulsową wyznacza się ze wzoru:gdzie: jest transformatą impulsu Diraca
( )
{
*
(
)
}
)
(
t
L
1G
s
X
s
g
=
−( )
{
}
( )
{
G s}
t s G L t g 1 1 ) ( 1 * ) ( − − =1
)
(
s
=
X
Rozkładamy na ułamki proste
)
1
(
1
)
1
(
s
T
sT
s
T
B
sT
A
s
T
sT
k
⋅
+
+
+
=
+
(17)BsT
s
T
A
k
=
(
1
+
)
+
(18)T
A
s
BT
A
k
=
(
+
)
+
(19)A
kT
T
A
k
=
⇒
=
(20)T
A
B
A
BT
+
=
0
⇒
=
−
(21)k
B
T
T
k
B
=
−
⇒
=
−
(22)s
T
k
sT
kT
s
T
sT
k
+
−
=
+
)
1
1
(
(23))
1
(
)
(
T t T te
k
ke
k
t
y
=
−
−=
−
− (24)Rys. 1 Odpowiedź skokowa.
Rys. 3 Odpowiedź liniowa
Zadanie 3 (charakterystyki czasowe układów)
Problem:Obliczyć charakterystykę skokową i impulsową układu dynamicznego o transmitancji
s
s
G
(
)
=
5
Rozwiązanie:
Transformata wymuszenia skokowego
[ ]
(
)
1
.
s
t
L
1
=
Transformata odpowiedzi skokowej
.
5
)
(
1
)
(
2s
s
G
s
s
H
=
=
Stosując odwrotne przekształcenie Laplace’a albo korzystając z tablicy transformat, łatwo znajdziemy charakterystykę skokową
[
(
)
]
5
5
(
)
)
(
1 1 2t
t
s
L
s
H
L
t
h
=
−=
−
=
1
Transmitancja członu całkującegoPatrz tablice transformat
dla t = 0[s] h(t) = 0 dla t = 0,2[s] h(t) = 1 dla t = 0,4[s] h(t) = 2 dla t = 0,6[s] h(t) = 3 dla t = 0,8[s] h(t) = 4 dla t = 1[s] h(t) = 5
[
5
(
)
]
5
(
)
)
(
)
(
t
t
t
dt
d
t
h
dt
d
t
g
=
=
1
=
1
.)
(
5
)
(
t
t
g
=
1
Charakterystyka impulsowa jest pochodną odpowiedzi skokowej.Rys.5.1 Charakterystyka skokowa
Zadanie 4 (charakterystyki czasowe układów)
Problem:
Obliczyć charakterystykę skokową i impulsową układu dynamicznego o transmitancji
)
2
3
)(
1
2
(
1
)
(
+
+
=
s
s
s
G
Rozwiązanie:Transformata wymuszenia skokowego
[ ]
(
)
1
.
s
t
L
1
=
Transformata odpowiedzi skokowej
.
)
2
3
)(
1
2
(
1
)
(
1
)
(
+
+
=
=
s
s
s
s
G
s
s
H
Stosując odwrotne przekształcenie Laplace’a albo korzystając z tablicy transformat, łatwo znajdziemy charakterystykę skokową
[
]
(
)
2
3
2
2
1
)
2
3
)(
1
2
(
1
)
(
)
(
3 2 2 1 1 1e
e
t
s
s
s
L
s
H
L
t
h
t t1
−
−
=
+
+
=
=
− − − − dla t = 0[s] h(t) = 0 dla t = 2[s] h(t) = 0,160 dla t = 4[s] h(t) = 0,334 dla t = 6[s] h(t) = 0,428 dla t = 8[s] h(t) = 0,471 dla t = 10[s] h(t) = 0,488 dla t = 12[s] h(t) = 0,496Charakterystykę impulsową znajdziemy stosując wzór:
− + − − = − − = = − − − − ) ( 3 2 ) ( 2 3 ) ( 2 1 ) ( 2 ) ( 2 1 ) ( 2 3 2 2 1 ) ( ) ( 3 2 2 1 3 2 2 1 t t e t t e t t e e dt d t h dt d t g t t t t 1 1 1
δ
δ
δ
. dla t = 0[s] g(t) = 0 dla t = 2[s] g(t) = 0,104 dla t = 4[s] g(t) = 0,066 dla t = 6[s] g(t) = 0,031 Charakterystyka impulsowa jest pochodną odpowiedzi skokowej. Transmitancja członu inercyjnego II rzędub
a
e
b
e
a
b
a
ab
s
b
s
a
s
L
bt at≠
−
−
+
=
+
+
− − −1
1
1
1
)
)(
(
1
1Impuls Diraca δ(t) jest pochodna skoku jednostkowego.
=
∞
≠
=
0
0
0
)
(
t
dla
t
dla
t
δ
dla t = 8[s] g(t) = 0,013 dla t = 10[s] g(t) = 0,005 dla t = 12[s] g(t) = 0,002Rys.6.1 Charakterystyka skokowa
Rys.6.2 Charakterystyka impulsowa
Zadanie 5 (charakterystyki czasowe układów)
Problem:
Znaleźć zależność między parametrami charakterystyki czasowej elementu oscylacyjnego i współczynnikami liczbowymi występującymi we wzorze na transmitancję operatorową.
1
2
1
)
(
2 2+
+
=
Ts
s
T
s
F
ξ
.Rozwiązanie:
Równanie charakterystyki czasowej elementu oscylacyjnego dla wymuszenia skokowego x = x0 1(t) wynika z następujących przekształceń:
(
)
[
]
= + + = ⋅ + + = 0 2 0 2 0 0 2 2 2 1 ) (ϖ
δ
ξ
T s s kx s x Ts s T k s Y(
)
(
)
2 0 2 0 0 2 0 2 0 01
ϖ
δ
δ
ϖ
δ
ϖ
+
+
+
+
+
+
+
=
s
s
C
s
B
s
A
δ0 + ϖ0 znajdujemy z warunku:(
)
2 2 2 0 2 0 0 2 2 0 2 01
2
2
T
s
T
s
s
s
s
+
δ
+
ϖ
=
+
δ
+
δ
+
ϖ
=
+
ξ
+
T
ξ
δ
0=
2 2 0 2 01
T
=
+
ϖ
δ
(
2)
2 2 01
1
ξ
ϖ
=
−
T
Stałe A, B, C wynoszą A = kx0 2 0 0 0 0 1ξ
ξ
ω
δ
− − = − = kx kx B 0kx
C
=
−
Równanie charakterystyki czasowej mając postać
⋅ − ⋅ − − =kx e− ⋅ t e− ⋅ t t y t t 0 0 2 0 sin cos 1 1 ) ( 0
ϖ
0ϖ
ξ
ξ
δ δ przekształcamy do postaci + − − = − sin( ) 1 1 ) ( 0 2 0 0ϕ
ω
ξ
δ t e kx t y t kąt ϕ znajdujemy z warunku:t
t
t
t
t
0 2 0 0 0 0cos
1
sin
cos
sin
sin
cos
)
sin(
ϖ
ξ
ϖ
ξ
ϖ
ϕ
ϖ
ϕ
ϕ
ϖ
+
+
=
=
⋅
+
⋅
=
+
(
sin
1
)
cos
0
sin
)
(cos
2 0 0+
−
−
⋅
=
−
ξ
ϖ
t
ϕ
ξ
ϖ
t
ϕ
ξ
ϕ
=
cos
ξ
≤
1
21
sin
ϕ
=
−
ξ
ξ
ξ
ϕ
= 1− 2 tg .Zadanie 6 (Charakterystyki czasowe układów)
Problem:Wyznaczyć odpowiedź układu przy zerowych warunkach początkowych, jeżeli dana jest transformata G (s) oraz sygnał wejściowy e(t).
( )
6
5
2
2+
+
−
=
s
s
s
s
G
e( )
t =5sin(t)1(t) Rozwiązanie:Oznaczamy przez y (t) sygnał wejściowy. Wykorzystując definicje transmitancji,
znajdujemy: Y
( )
s =G( ) ( )
s ⋅E s( )
t
L
{
G
( ) ( )
s
E
s
y
=
−1}
(1) Powstaje zależność( )
{
}
1
5
)
sin(
5
2 1+
=
=
−s
t
L
s
E
(2) Transformata Lapace’aω
ω
ω
+
=
− 2 1(sin
)
s
t
L
Podstawiając równanie (2) oraz transmitancje od definicji transmitancji otrzymujemy Otrzymujemy równanie:
( )
(
(
)(
)
)
(
)(
(
)
(
)
)
(
)(
)(
)
+
−
+
=
−
−
+
−
=
−
+
+
−
=
− − −1
1
2
5
1
2
2
2
5
1
6
5
2
5
1 2 1 2 2 1s
s
s
L
s
s
s
s
L
s
s
s
s
L
t
y
(3)Wykonujemy przekształcenia matematyczneax2+bx+c=a
(
x−x1)(
x−x2)
przy czym x 1 i x 2 to pierwiastki rów. kwadratowego, po czym skracamy z licznik
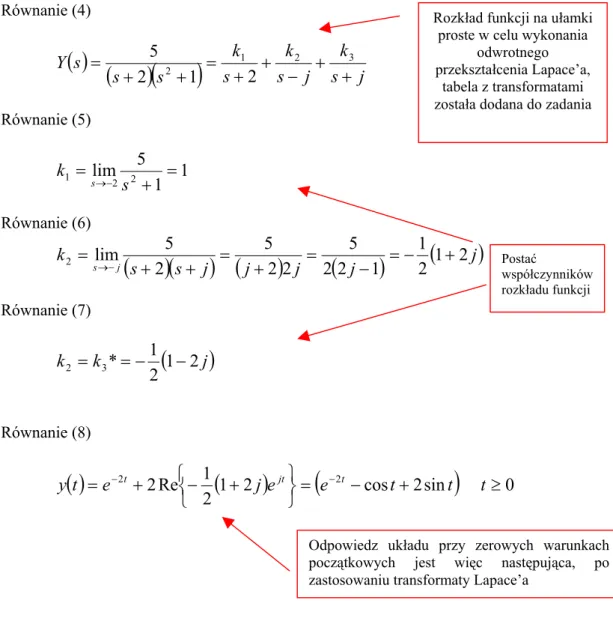
Równanie (4) Rozkład funkcji na ułamki proste w celu wykonania
odwrotnego przekształcenia Lapace’a,
tabela z transformatami została dodana do zadania
( ) ( )
(
)
s j k j s k s k s s s Y + + − + + = + + = 1 2 3 2 1 2 2 5 Równanie (5)1
1
5
lim
2 2 1=
→−+
=
s
k
s Równanie (6)(
s
)(
s
j
) (
j
)
j
(
j
)
(
j
)
j s2
1
2
1
1
2
2
5
2
2
5
2
5
lim
2=
→−+
+
=
+
=
−
=
−
+
k
Postać współczynników rozkładu funkcji Równanie (7)(
j
)
k
k
1
2
2
1
*
3 2=
=
−
−
Równanie (8)( )
t
e
(
j
)
e
(
e
t
t
)
y
t1
2
jt tcos
2
sin
2
1
Re
2
2 2=
−
+
−
+
+
=
− − t ≥0Odpowiedz układu przy zerowych warunkach początkowych jest więc następująca, po zastosowaniu transformaty Lapace’a
Zadanie 7 (Charakterystyki czasowe układów)
Problem:Wyznaczyć odpowiedź układu przy zerowych warunkach początkowych, jeżeli dana jest transformata G (s) oraz sygnał wejściowy e(t).
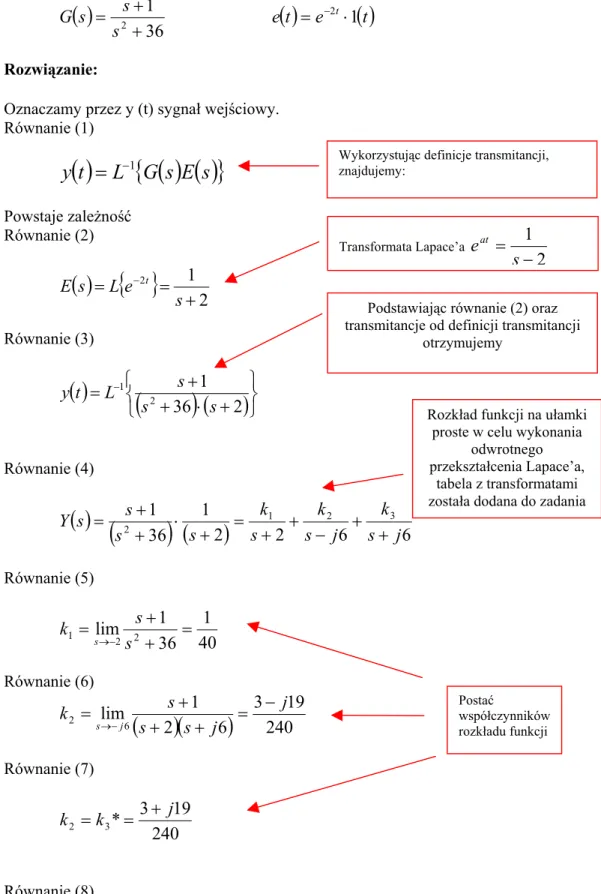
( )
36
1
2+
+
=
s
s
s
G
e
( )
t
=
e
−2t⋅
1
( )
t
Rozwiązanie:Oznaczamy przez y (t) sygnał wejściowy. Równanie (1)
( )
t
L
{
G
( ) ( )
s
E
s
}
y
=
−1 Powstaje zależność Równanie (2)( )
{ }
2
1
2+
=
=
−s
e
L
s
E
t Równanie (3)( )
(
)
(
)
+
⋅
+
+
=
−2
36
1
2 1s
s
s
L
t
y
Wykorzystując definicje transmitancji, znajdujemy: Transformata Lapace’a
2
1
−
=
s
e
atPodstawiając równanie (2) oraz transmitancje od definicji transmitancji
otrzymujemy Równanie (4)
( )
(
)
(
)
6 6 2 2 1 36 1 1 2 3 2 s j k j s k s k s s s s Y + + − + + = + ⋅ + + =Rozkład funkcji na ułamki proste w celu wykonania
odwrotnego przekształcenia Lapace’a,
tabela z transformatami została dodana do zadania
Równanie (5)
40
1
36
1
lim
2 2 1+
=
+
=
− →s
s
k
s Równanie (6) Postać współczynników rozkładu funkcji(
)(
)
240
19
3
6
2
1
lim
6 2j
j
s
s
s
k
j s−
=
+
+
+
=
− → Równanie (7)240
19
3
*
3 2j
k
k
=
=
+
Równanie (8)( )
−
+
+
=
+
+
−
=
e
−j
e
e
−t
t
t
y
t j tsin
6
120
19
6
cos
40
1
40
1
240
19
3
Re
2
40
1
2 6 2Odpowiedz układu przy zerowych warunkach początkowych jest więc następująca, po zastosowaniu transformaty Lapace’a
0 ≥