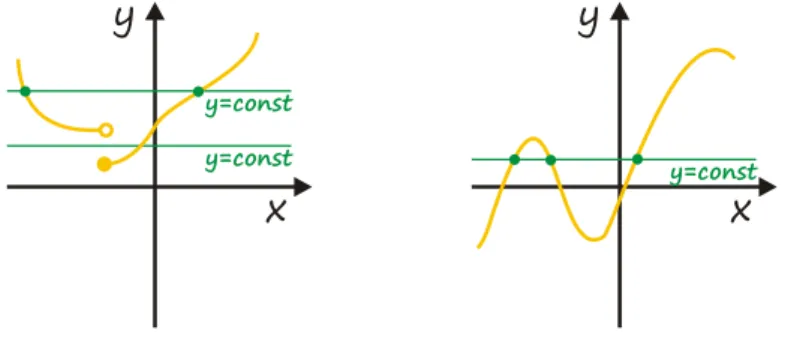Funkcje hiperboliczne

(1)

Funkcje jednej zmiennej rzeczywistej

Autorzy:

Anna Barbaszewska-Wiśniowska

(2)

Spis treści

Pojęcie funkcji. Dziedzina i przeciwdziedzina Wykres funkcji

Przekształcanie wykresów funkcji Sposoby zadawania funkcji Dziedzina naturalna funkcji Suriekcja, iniekcja, bijekcja Restrykcja (zawężenie) funkcji

Podstawowe własności funkcji: okresowość, parzystość, nieparzystość, ograniczoność, monotoniczność Algebraiczne działania na funkcjach

Identyczność Składanie funkcji

Pojęcie funkcji odwrotnej do danej

Funkcje cyklometryczne. Definicje, wykresy, podstawowe własności

Tożsamości cyklometryczne. Zadania z zastosowaniem funkcji cyklometrycznych Podstawowe funkcje elementarne

(3)

Pojęcie funkcji. Dziedzina i przeciwdziedzina

W otaczającej nas rzeczywistości zarówno fizycznej jak i społecznej, występuje wiele zależności pomiędzy różnymi zjawiskami, obiektami czy wielkościami. Na przykład, podczas jazdy samochodem długość przebytej drogi zależy od czasu podróży. Każdej chwili odpowiada, przebyta dotąd droga. W sytuacji, gdy jedziemy ze stałą prędkością dystans ten możemy bardzo łatwo obliczyć mnożąc prędkość przez czas.

W sytuacji realnej najczęściej prędkość jest zmienna, jedziemy raz szybciej raz wolniej, co parę godzin zatrzymujemy się, jednakże i wówczas każdej chwili podróży możemy przyporządkować liczbę przejechanych kilometrów. Jako przykłady z innej dziedziny zauważmy, że każdemu członkowi danej społeczności (np. każdemu obywatelowi Polski) odpowiada jego data urodzenia. Każdemu obywatelowi nadawany jest też numer identyfikacyjny PESEL, a każdemu studentowi danego wydziału AGH odpowiada numer jego indeksu (tzw. numer albumu). We wszystkich wspomnianych przykładach mamy do czynienia z odpowiedniością pomiędzy elementami dwóch zbiorów oraz .

W przypadku podróży oznacza przedział liczbowy określający czas jazdy od chwili początkowej, która może być przyjęta

umownie, jako czas do końca podróży . Możemy wówczas zapisać ). to zbiór nieujemnych liczb

rzeczywistych wyrażających długość przebytej drogi (np. w kilometrach). W drugim i trzecim przykładzie jest zbiorem wszystkich obywateli RP, a w czwartym zbiorem wszystkich studentów wydziału.

Zauważmy, że we wszystkich tych przypadkach każdemu elementowi każdemu elementowi ze zbioru ze zbioru odpowiada tylko jeden element odpowiada tylko jeden elementyy ze zbioru ze zbioru .. Faktycznie, jeden człowiek nie może mieć dwóch różnych dat urodzenia, w każdej chwili podróży stwierdzamy, że przejechaliśmy konkretną liczbę kilometrów itd.Ta jedyność elementu Ta jedyność elementu odpowiadającego danemu elementowi odpowiadającego danemu elementowi xx ma kluczowe znaczenie w ma kluczowe znaczenie w pojęciu funkcji.

pojęciu funkcji.

DEFINICJA

Definicja 1: Funkcja

Niech będzą dane niepuste zbiory i . Funkcją odwzorowującą zbiór

Funkcją odwzorowującą zbiór w zbór w zbór (co zapisujemy ) nazywamy przyporządkowanie każdemu elementowi ze zbioru dokładnie jednego elementu ze zbioru . Element ze zbioru nazywamy argumentem funkcjiargumentem funkcji a jedyny element ze zbioru , który został przyporządkowany elementowi oznaczamy przez i nazywamy wartością funkcji wartością funkcji dla argumentu

dla argumentu .

Zbiór nazywamy dziedziną funkcji dziedziną funkcji i oznaczamy przez . Zbiór obrazów wszystkich argumentów czyli zbiór elementów nazywamy przeciwdziedzinąprzeciwdziedziną lub zbiorem wartości funkcji zbiorem wartości funkcji i oznaczamy . Przeciwdziedzina jest zawsze podzbiorem zbioru . Rysunek 1: Funkcja

X

Y

X

t = 0

t = T

X = [0, T] Y

X

x

X

Y

y

X Y

X

Y

f : X → Y

x

X

y

Y

x

X

y

Y

x

f(x)

f

x

X

f

D

f

{f(x) : x ∈ X}

f

R

f

Y

f : X → Y

(4)

UWAGA

Uwaga 1: Oznaczenia i nazewnictwo

Gdy mówimy o jednej funkcji, oznaczamy ją pojedynczą literą (tu literą , natomiast gdy rozważamy więcej funkcji, możemy zastosować zapis indeksowany , , . itd. lub użyć innych liter np. , , , . Przez (co odczytujemy : „ od ”) oznaczamy wartość funkcji dla elementu . Często mówimy też, że jest wartością funkcji w punkcie w punkcie , chociaż w ogólnym przypadku element x z punktem w sensie geometrycznym może nie mieć nic wspólnego (tak właśnie jest w przykładzie z Peselem, gdzie oznacza człowieka). Czasami też na używa się określenia: „obraz elementu obraz elementu przez przez funkcję

funkcję ”.

Jeżeli zbiory i są podzbiorami zbioru liczb rzeczywistych to mówimy, że jest funkcją rzeczywistą jest funkcją rzeczywistą (myśląc o jej wartości ze zbioru liczb rzeczywistych) zmiennej rzeczywistejzmiennej rzeczywistej (myśląc o jej argumentach ze zbioru liczby rzeczywistych). Możemy, więc zanotować następującą definicję.

DEFINICJA

Definicja 2: Funkcja rzeczywista zmiennej rzeczywistej

Niech oraz będą niepustymi podzbiorami liczb rzeczywistych . Funkcją rzeczywistą zmiennej rzeczywistej

Funkcją rzeczywistą zmiennej rzeczywistej prowadzącą ze zbioru w zbiór (co zapisujemy ) nazywamy

przyporządkowanie każdej liczby ze zbioru dokładnie jednej liczby ze zbioru .

Rysunek 2: Funkcja rzeczywista

UWAGA

Uwaga 2:

Definicje i określają funkcje w sposób dynamiczny. Zbiór możemy traktować jako zbiór wyjściowy, początkowy zbiórzbiór danych

danych a funkcję jako narzędzie do przetwarzania jego elementów w elementy zbioru końcowego .

f

1

f

2

f

3

g h u v

f(x)

f

x

f

x

f(x)

x

f(x)

x

f

X Y

R

f

X

Y

R

X

Y

f : X → Y

x

X

(a, b)

x

y

X Y

X

Y

f

(x, y)

X

Y

x

X

f

x

( , )

x

1

y

1

( , )

x

1

y

2

y

1

y

2

X

Y

(6)

DEFINICJA

Definicja 4: Wykres funkcji

Wykres funkcji jest to zbiór par uporządkowanych

Rysunek 3: Wykres funkcji, dziedzina i przeciwdziedzina funkcji

UWAGA

Uwaga 6:

Na płaszczyźnie kartezjańskiej z przyjętym układem współrzędnych dziedzina funkcji leży na osi . Jest ona rzutem prostokątnym wykresu na tę oś. Podobnie, rzutując wykres na oś otrzymujemy zbiór wartości funkcji.

UWAGA

Uwaga 7:

Własność prawostronnej jednoznaczności geometrycznie oznacza, że każda prosta równoległa do osi (prosta „pionowa”

o równaniu , gdzie jest skrótem od słowa constans, stała) może przeciąć wykres funkcji, co najwyżej w

jednym punkcie. Daje to nam łatwe kryterium rozstrzygające, czy dany zbiór przedstawiony w układzie współrzędnych jest wykresem pewnej funkcji.

f : X → Y

{(x, y) : x ∈ X, y ∈ Y , y = f(x)}

x0y

0x

0y

0y⃗

x = const

const

(7)

PRZYKŁAD

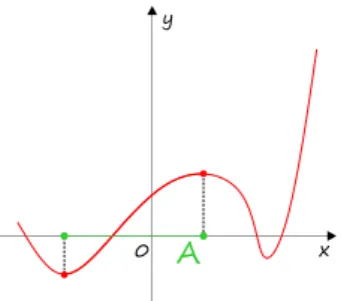
Przykład 1:

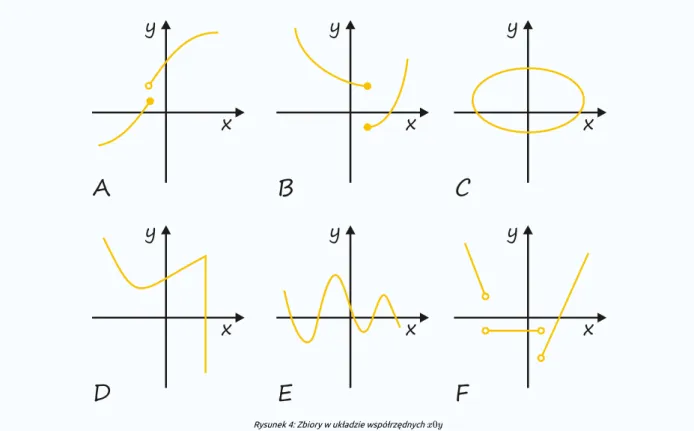
Stwierdzimy, które z naszkicowanych zbiorów są wykresami funkcji zmiennej .

Rysunek 4: Zbiory w układzie współrzędnych

Rozwiązanie Rozwiązanie

Zbiory , i nie przedstawiają wykresów funkcji, gdyż znajdziemy takie proste pionowe, które mają z nimi więcej niż po jednym punkcie wspólnym. W przypadku i są to dwa punkty, a w przypadku aż nieskończenie wiele.

Rysunek 5: Ilustracja rozwiązania graficznego

Pozostałe wykresy: , , są wykresami pewnych funkcji zmiennej .

x

x0y

B C D

B C

D

(8)

ZADANIE

Zadanie 1:

Treść zadania: Treść zadania:

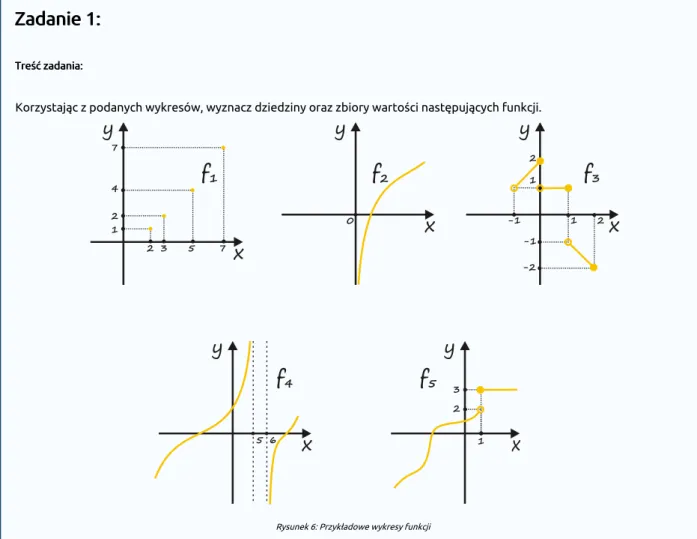
Korzystając z podanych wykresów, wyznacz dziedziny oraz zbiory wartości następujących funkcji.

Rysunek 6: Przykładowe wykresy funkcji

Rozwiązanie: Rozwiązanie:

Rzutując wykres funkcji na oś otrzymujemy jej dziedzinę utworzoną tu z jedynie czterech liczb naturalnych. Mamy,

więc .

Zbiór wartości odczytujemy po zrzutowaniu wykresu na oś .

Podobnie postępując określamy dziedziny pozostałych funkcji. I tak, jest przedziałem obustronnie otwartym , a jej zbiór wartości jest to cały zbiór liczb rzeczywistych .

jest przedziałem lewostronnie otwartym , a jej zbiór wartości jest sumą dwóch przedziałów oraz

.

jest sumą przedziałów oraz , a przeciwdziedziną jest cały zbiór liczb rzeczywistych .

jest zbiorem liczb rzeczywistych , a jest sumą przedziału otwartego i zbioru jednoelementowego .

f

1

0x⃗

= {2, 3, 5, 7}

D

f1

{1, 2, 4, 7}

0y⃗

D

f2

(0, +∞)

R

f2

R

D

f3

(−1, 2]

R

f3

[−2, −1)

[1, 2]

D

f4

(−∞, 5)

(6, +∞)

f

4

R

D

f5

R R

f5

(−∞, 2)

{3}

(9)

ZADANIE

Zadanie 2:

Student uprawiający jogging naszkicował wykres funkcji przedstawiającej jak zmieniała się jego odległość od akademika podczas pewnego treningu.

Rysunek 7: Funkcja opisująca odległość studenta od akademika podczas joggingu Odpowiedzmy na poniższe pytania:

1. Po ilu minutach rozgrzewki student zaczął biec zdecydowanie szybciej i jak długo utrzymywał to większe tempo? 2. Kiedy zaczął zawracać?

3. Gdzie był po 45 minutach treningu? 4. Kiedy i na jak długo zatrzymał się? Rozwiązanie:

Rozwiązanie:

Analizując wykres łatwo możemy stwierdzić, że po 20 minutach student przyśpieszył, po pół godzinie (dalej utrzymując to większe tempo) zawrócił, by po 45 minutach znaleźć się przy akademiku. Drugą, krótszą pętlę trasy biegł znacznie wolniej. Po godzinie od początku treningu zatrzymał się na 10 minut, a następnie wrócił do akademika w równym) wolniejszym tempie.

UWAGA

Uwaga 8:

Ten elementarny przykład uświadamia nam jak wiele różnorodnych informacji związanych ze zjawiskami opisywanymi przez funkcję możemy odczytać z jej wykresu. Dlatego tez należy zapoznać się z wykresami pewnych typowych funkcji

elementarnych i zapamiętać ich kształt.

Przekształcanie wykresów funkcji

W wielu przypadkach funkcja, którą badamy, „nieznacznie” różni się od pewnej funkcji o znanym wykresie. Wówczas możemy narysować jej wykres, stosując odpowiednie przekształcenie znanego wykresu funkcji .

_f

f

(10)

UWAGA

Uwaga 9: Przekształcanie wykresów funkcji

Zakładamy, że znamy wykres , .

Aby otrzymać wykres funkcji dokonujemy translacjitranslacji wykresu funkcji o wektor .

Wykres funkcji otrzymujemy poprzez translacjętranslację wykresu funkcji o wektor .

Funkcję rysujemy odbijając symetrycznie względem osi część wykresu funkcji leżącą pod tą osią i

pozostawiając resztę wykresu funkcji bez zmian.

Natomiast wykres funkcji powstanie poprzez „zignorowanie” części wykresu leżącej po lewej stronie osi i

umieszczenie tam odbitej symetrycznie względem tej osi części wykresu dla (o ile wyjściowa funkcja była określona

dla ).

Wykres funkcji powstaje poprzez odbicie symetryczne wykresu funkcji odbicie symetryczne wykresu funkcji względem osi względem osi .

f : R ⊃

D

f

→ R

f : x ↦ f(x)

g : x ↦ f(x) + a, a ∈ R

f

v⃗

= [0, a]

h : x ↦ f(x + a), a ∈ R

f

v⃗

= [−a, 0]

k : x → |f(x)|

0x⃗

f

l : x ↦ f(|x|)

0y⃗

x ≥ 0

f

x ≤ 0

m : x ↦ −f(x)

f

0x

(11)

PRZYKŁAD

Przykład 2: Przekształcanie wykresów funkcji

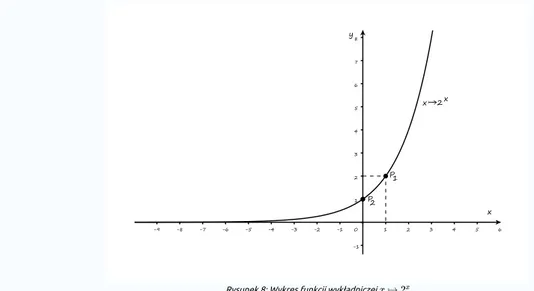
Naszkicujemy wykres funkcji ,

Rysujemy znany wykres funkcji wykładniczej o podstawie 2 (większej od 1), zaznaczając na nim przynajmniej dwa

jego punkty charakterystyczne, a mianowicie .

Rysunek 8: Wykres funkcji wykładniczej

Następnie przesuwamy ten wykres „w poziomie do tyłu” o wektor otrzymując wykres (naszkicowany na

czerwono).

Rysunek 9: Translacja wykresu funkcji o wektor

f : R ∋ x ↦ 2

x+3

x ↦ 2

x

= (0, 1),

= (1, 2)

P

1

P

2 x ↦ 2x

= [−3, 0]

v⃗

f

x ↦ 2x _v⃗_{= [−3, 0]}

(12)

ZADANIE

Zadanie 3:

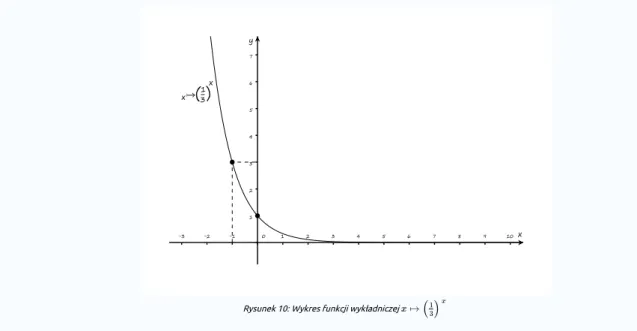
Naszkicujemy wykres funkcji .

Aby naszkicować wykres , wychodzimy od znanego wykresu funkcji wykładniczej o podstawie ułamkowej z

przedziału , na którym również zaznaczamy przynajmniej dwa jego punkty charakterystyczne.

Rysunek 10: Wykres funkcji wykładniczej

W następnym kroku przesuwamy ten wykres „w poziomie do przodu” o wektor otrzymując wykres funkcji

(naszkicowany na zielono) i na koniec dokonujemy translacji pomocniczego wykresu (zielonego) otrzymując wykres funkcji (czerwony).

Rysunek 11: Translacje wykresu funkcji kolejno o wektory oraz

Zauważmy, że wykres funkcji mogliśmy otrzymać szybciej przesuwając wykres pomocniczy od razu o wektor

czyli .

g : R ∋ x ↦

( )

1

+ 2

3 x−1

Zadanie 4:

Naszkicujemy wykres funkcji .

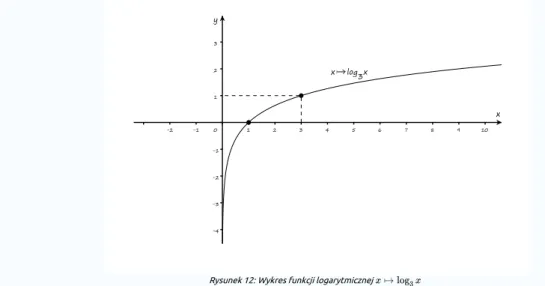
Aby naszkicować wykres funkcji , szkicujemy znany wykres funkcji logarytmicznej o podstawie

3 (większej od 1) zaznaczając jego punkty charakterystyczne.

Rysunek 12: Wykres funkcji logarytmicznej

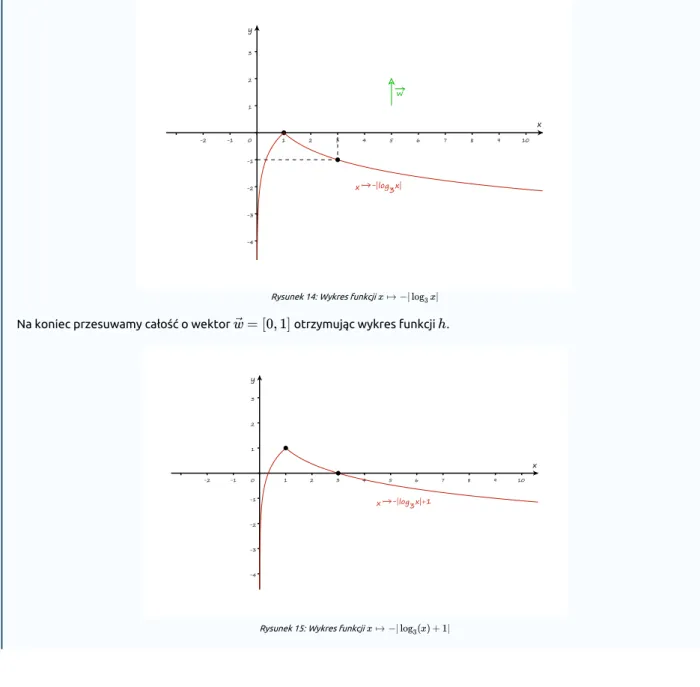
Tę część wykresu , gdzie funkcja przyjmuje wartości ujemne („leżącą pod osią ”) przekształcamy poprzez

symetrię względem a resztę pozostawiamy bez zmian, otrzymując wykres funkcji .

Rysunek 13: Transformacja wykresu funkcji w wykres funkcji Aby otrzymać wykres

przekształcamy przez symetrię osiowa względem wykres .

h :

R

+

∋ x ↦ 1 − |

_log

(x)|

3

h :

R

+

∋ x ↦ 1 − |

_log

x|

(14)

Rysunek 14: Wykres funkcji

Na koniec przesuwamy całość o wektor otrzymując wykres funkcji .

Sposoby zadawania funkcji

UWAGA

Uwaga 10: Sposoby przedstawienia funkcji

Funkcję możemy określić na wiele sposobów: poprzez podanie przepisu słownego, wykresu, tabeli, diagramu, wzoru itp.

x ↦ −|log3x|

= [0, 1]

w⃗

h

(15)

(1) (2) (3) (4)

PRZYKŁAD

Przykład 3:

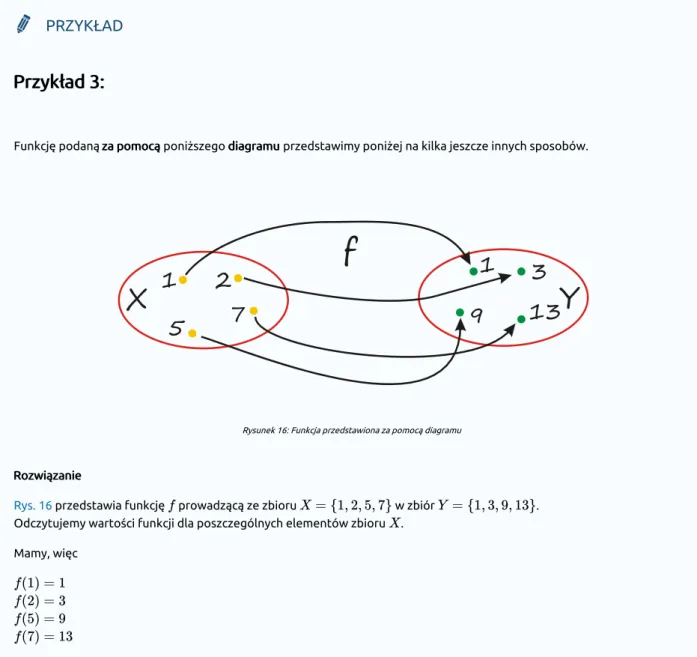
Funkcję podaną za pomocąza pomocą poniższego diagramudiagramu przedstawimy poniżej na kilka jeszcze innych sposobów.

Rysunek 16: Funkcja przedstawiona za pomocą diagramu

Rys. 16 przedstawia funkcję prowadzącą ze zbioru w zbiór . Odczytujemy wartości funkcji dla poszczególnych elementów zbioru .

Mamy, więc

Funkcję możemy opisać: słownie

słownie: jest funkcją przyporządkowującą każdej liczbie ze zbioru różnicę liczby od niej dwa razy większej i jedynki za pomocą

za pomocą jednego z następujących wzorówwzorów:

za pomocą wykresu za pomocą wykresu

Rysunek 17: Funkcja przedstawiona za pomocą wykresu w kartezjańskim układzie współrzędnych

f

X = {1, 2, 5, 7}

Y = {1, 3, 9, 13}

X

f(1) = 1

f(2) = 3

f(5) = 9

f(7) = 13

f

{1, 2, 5, 7}

f : X → Y , f(x) = 2x − 1 gdzie X = {1, 2, 5, 7} Y = {1, 3, 9, 13}

f : X → Y , x ↦ 2x − 1 gdzie X = {1, 2, 5, 7} Y = {1, 3, 9, 13}

f : X ∋ x ↦ (2x − 1) ∈ Y gdzie X = {1, 2, 5, 7} Y = {1, 3, 9, 13}

f : X → Y , y = 2x − 1 gdzie X = {1, 2, 5, 7} Y = {1, 3, 9, 13}

(16)

Dziedzina naturalna funkcji

UWAGA

Uwaga 11: O dziedzinie naturalnej

Ścisłe zdefiniowanie funkcji wymaga podania dwóch zbiorów (wyjściowego i końcowego ) i określenia przepisu w jaki sposób ta funkcja przekształca elementy zbioru w elementy . Jeżeli zbiory i nie są z góry zadane (z czym często

spotykamy się w zadaniach sformułowanych tak: dana jest funkcja lub ) i funkcja podana jest tylko

za pomocą pewnego wzoru (przepisu), to wówczas przyjmujemy, że dziedziną funkcji jest zbiór tych wszystkich liczb rzeczywistych , dla których wyrażenie ma sens liczbowy. Taki zbiór nazywamy dziedziną naturalną funkcjidziedziną naturalną funkcji. Jako zbiór końcowy przyjmujemy wówczas zbiór wszystkich liczb rzeczywistych.

X

Y

X

Y

X Y

y = f(x)

f : x → f(x)

f

x

f(x)

Y

(17)

PRZYKŁAD

Przykład 4: Wyznaczanie dziedziny naturalnej funkcji

Wyznaczymy dziedzinę naturalną funkcji danej wzorem:

Logarytmy możemy obliczać jedynie tylko z liczb dodatnich. Musimy, więc wyznaczyć wszystkie te liczby, dla których

wyrażenie logarytmowane jest większe od zera. Rozwiązując nierówność wykorzystamy np. wzory

Viete’a

INFORMACJA DODATKOWA

Informacja dodatkowa 1:

Informacja dodatkowa 1: Wzory Viete’a

Wzory Viete’a

Pierwiastki trójmianu kwadratowego ,

spełniają warunki .

Mamy, więc , . Rozwiązanie nierówności znajdujemy na osi liczbowej pamiętając, aby wykres wielomianu

(funkcji kwadratowej) zacząć rysować „od dołu”. Ramiona paraboli skierowane są w dół, gdyż

Rysunek 18:

Otrzymujemy więc .

Odpowiedź Odpowiedź

Dziedziną naturalną funkcji jest przedział otwarty .

y =

log

3

(− + 5x + 6),

x

2

− + 5x + 6 > 0

x

2

y =

log

3

(− + 5x + 6)

x

2

(−1, 6)

(18)

ZADANIE

Zadanie 5:

Wyznaczymy dziedzinę naturalną funkcji danej wzorem .

Aby znaleźć dziedzinę funkcji , musimy rozpatrzyć dwa warunki. Po pierwsze: mianownik musi być

różny od zera (tu jest to spełnione w sposób oczywisty) i po drugie: wyrażenie musi należeć do dziedziny funkcji

, czyli muszą być spełnione dwie nierówności: oraz .

Rozwiązując te nierówności kolejno otrzymujemy:

oraz , czyli oraz , stąd oraz , więc Odpowiedź

Odpowiedź Dziedziną naturalną badanej funkcji jest cały zbiór liczb rzeczywistych.

y = arcsin

2x 1+x2

y = arcsin

2x 1+x2

1 + x

2 2x 1+x2

arkussinus

2x

≥ −1

1+x2 _1+x2x2

≤ 1

(19)

ZADANIE

Zadanie 6:

Wyznaczymy dziedzinę naturalną funkcji danej wzorem .

Dla funkcji podobnie jak w przypadku bb. rozważamy dwa warunki: mianownik musi być różny od zera

oraz wyrażenie musi należeć do dziedziny funkcji , którą jest przedział . Mamy więc:

czyli oraz

.

Tę nierówność podwójną możemy rozwiązać klasycznie, sprowadzając do wspólnego mianownika jak w przypadku b. , ale możemy też wykorzystać własność wartości bezwzględnej.

, ,

, .

Korzystając z interpretacji geometrycznej wartości bezwzględnej wiemy, że jest równa odległości od na osi liczbowej. Poszukujemy takich , których odległość od liczby jest większa lub równa od jedynki. Przedstawiając tę sytuację na osi liczbowej otrzymujemy rozwiązanie

Rysunek 19:

.

Uwzględniając warunek otrzymujemy odpowiedź.

Dziedziną funkcji jest suma przedziałów .

Suriekcja, iniekcja, bijekcja

y = arccos

1 2−x

y = arccos

1 2−x

2 − x

1 2−x

arkuskosinus

[−1, 1]

2 − x ≠ 0

x ≠ 2

−1 ≤

1

≤ 1

2−x

|

1

| ≤ 1

2−x

|2 − x| ≥ 1

| − (x − 2)| ≥ 1

|x − 2| ≥ 1

|x − |

x

0

x x

0

x

0

= 2

x ∈ (−∞, 1] ∪ [3, +∞)

x ≠ 2

y = arccos

1 2−x

(−∞, 1] ∪ [3, ∞)

(20)

DEFINICJA

Definicja 5: Suriekcja czyli funkcja „na”

Mówimy, że jest suriekcjąsuriekcją, (czyli funkcją „na”funkcją „na”) wtedy i tylko wtedy, gdy jej zbiór wartości jest równy zbiorowi końcowemu .

Zapisujemy wówczas co odczytujemy: funkcja funkcja prowadzi ze zbioru prowadzi ze zbioru na zbiór na zbiór .

UWAGA

Uwaga 12:

Wiemy, że geometrycznie zbiór wartości funkcji jest rzutem prostopadłym wykresu na oś . Stąd jest

suriekcją, gdy rzut jej wykresu na oś pokrywa się ze zbiorem .

Rysunek 20: suriekcja

Rysunek 21: nie jest suriekcją

f : X → Y

Y

f : X

−→

na

Y

f

X

Y

0y⃗

f : X → Y

0y⃗

Y

: X Y f1 −→na : X → Y f2

(21)

PRZYKŁAD

Przykład 5:

Niech , . Zbadamy, czy , jest suriekcją.

Rozwiązanie Rozwiązanie Szkicujemy wykres .

Z wykresu odczytujemy, że zbiór wartości funkcji (rzut jej wykresu na oś ) to przedział , który jest silnie

zawarty w zbiorze , zatem nie jest suriekcją.

ZADANIE

Zadanie 7:

Niech , . Zbadamy czy , jest suriekcją.

Wykres funkcji powstaje poprzez przesunięcie „w poziomie” o wektor wykresu funkcji wykładniczej ,

więc rzuty prostopadłe na oś obu wykresów są identyczne. Obie funkcje mają te same zbiory wartości. Wiedząc, że zbiór

wartości funkcji wykładniczej jest przedziałem równym całemu zbiorowi wnioskujemy, że jest suriekcją.

INFORMACJA DODATKOWA

Informacja dodatkowa 2:

Własność suriektywności zależy od tego, jaki zbiór przyjmiemy za zbiór końcowy . Gdybyśmy w przykładzie 1 jako wzięli przedział funkcja byłaby suriekcją. W szczególności: każda funkcja może być traktowana jako suriekcja na swójkażda funkcja może być traktowana jako suriekcja na swój zbiór wartości zbiór wartości.

X = R Y = (−∞, 3]

f : X → Y f(x) = 2 − |x|

f

0y⃗

(−∞, 2]

(−∞, 3]

f

X = R Y = (0, ∞)

f : X → Y f(x) = 3

x+5

f

v⃗

= [5, 0]

x → 3

x

0y⃗

x → 3

x

_{(0, ∞)}

_Y

_f

Y

(−∞, 2]

(22)

DEFINICJA

Definicja 6: Funkcja różnowartościowa, iniekcja

Mówimy, że jest iniekcjąiniekcją (funkcją różnowartościowąfunkcją różnowartościową) wtedy i tylko wtedy, gdy dla każdych elementów

stąd, że wynika, że Interpretacja geometryczna różnowartościowości.

Funkcja jest różnowartościowa gdy dowolna prosta pozioma o równaniu przecina wykres w co najwyżej jednym

punkcie.

Rysunek 23: Funkcje różnowartościowe. Każda prosta pozioma przecina wykres w co najwyżej jednym punkcie

Rysunek 24: Funkcje nieróżnowartościowe. Istnieją proste poziome przecinające wykres w kilku punktach

PRZYKŁAD

Przykład 6:

Funkcje logarytmiczna, wykładnicza, funkcja potęgowa postaci dla nieparzystych, są różnowartościowe. Nie są różnowartościowe funkcje trygonometryczne i funkcje potęgowe postaci dla -parzystych.

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: Warunek równoważny różnowartościowości

Warunek równoważny różnowartościowości

Funkcja jest funkcją różnowartościową wtedy i tylko wtedy, gdy dla każdych dwóch elementów

zachodzi warunek: stąd, że wynika, że .

f : X → Y

, ∈ X

x

1

x

2

x

1

≠

x

2

f( ) ≠ f( )

x

1

x

2

f

y = const

f

y = const

y = x

n

_n

y = x

n

_n

f : X → Y

x

1

, ∈ X

x

2

f( ) = f( )

x

1

x

2

x

1

=

x

2

(23)

DEFINICJA

Definicja 7: Funkcja różnowartościowa na zbiorze

Mówimy, że funkcja funkcja jest różnowartościowa w zbiorze różnowartościowa w zbiorze zawartym w dziedzinie zawartym w dziedzinie wtedy i tylko wtedy, gdy jej restrykcja do zbioru jest funkcja różnowartościową.

Rysunek 25: Funkcja nieróżnowartościowa, która jest różnowartościowa na zbiorze

PRZYKŁAD

Przykład 7:

Pokażemy, że funkcja jest różnowartościowa.

Skorzystamy z twierdzenia Warunek równoważny różnowartościowości. Dziedziną naturalną danej funkcji jest zbiór liczb

rzeczywistych. Obierzmy dwie takie liczby i załóżmy, że . Należy pokazać, że .

Mamy , .

Założona równość przybiera tu postać .

Logarytmując obie strony (przy podstawie 3) otrzymujemy .

Korzystając z własności logarytmu dla i otrzymujemy

, , .

DEFINICJA

Definicja 8: Bijekcja

Funkcję nazywamy bijekcją wtedy i tylko wtedy, gdy jest funkcją różnowartościową oraz „na”, czyli jest zarówno iniekcją jak i suriekcją jednocześnie.

Restrykcja (zawężenie) funkcji

f

A

y = 3

2x+5

, ∈ R

x

3

2 +5x1

2

2 = 2

x

1

x

2

=

x

1

x

2

f : X → Y

(24)

DEFINICJA

Definicja 9: Równość funkcji

Mówimy, że funkcje funkcje i i są równe są równe wtedy i tylko wtedy, gdy mają te same dziedziny oraz dla każdego punktu wspólnej

dziedziny mają te same wartości. Możemy to zapisać i dla każdego mamy

DEFINICJA

Definicja 10: Restrykcja funkcji

Niech będzie dana funkcja oraz zbiór .

Funkcje

Funkcje taką, że dla każdego zachodzi równość nazywamy restrykcjąrestrykcją lub zawężeniemzawężeniem funkcji

funkcji do zbioru do zbioru i oznaczamy

Rysunek 26: Restrykcja funkcji, funkcja jest zawężeniem funkcji do zbioru

PRZYKŁAD

Przykład 8:

Dane są trzy funkcje:

.

Wśród funkcji , , znajdź parę funkcji równych sobie oraz przedstaw funkcję jako restrykcję funkcji do pewnego zbioru .

Funkcje , , będziemy rozpatrywać w ich dziedzinach naturalnych. Aby zbadać równość funkcji musimy wyznaczyć (i porównać) te dziedziny oraz porównać wartości.

jest zbiorem tych wszystkich , dla których . Mamy , więc .

Wyrażenie ma sens wówczas, gdy oraz .

Rozwiązując ,

f g

f = g ⇔

D

f

=

D

g

x ∈

D

f

=

D

g

f(x) = g(x).

f : X → Y

A ⊂ X

g : A → Y

x ∈ A

x

3

+ x ≠ 0

x

3

+ x = x( + 1)

x

2

D

f

= R ∖ {0}

3

log3x2_x3+1_+x

_x

3

_{+ x ≠ 0}

x2+1

_{> 0}

+x x3

> 0

+1 x2 +x x3

> 0

+1 2

(25)

, , .

Zatem .

Dziedzina funkcji jest różna od dziedziny funkcji , czyli funkcje i nie spełniają pierwszego warunku z definicji równości funkcji, a więc nie mogą być równe.

Wyznaczając dziedzinę funkcji zakładamy:

Zatem .

Dziedziny funkcji i są równe, a więc należy jeszcze sprawdzić drugi warunek definicji o równości funkcji, czyli porównać ich wartości

Weźmy dowolne , korzystając z własności logarytmów mamy:

, .

Widzimy więc, że dla każdego , czyli uwzględniając równość dziedzin wnioskujemy, że funkcje i

są równe.

Zauważmy, że funkcje oraz można zapisać następująco: ,

.

Funkcja jest określona dla . Po przekształceniu otrzymujemy . Co możemy zanotować:

.

Funkcja jest więc restrykcją (zawężeniem) funkcji do zbioru , co zapisujemy symbolicznie . Odpowiedź

Odpowiedź

Dwie funkcje równe to funkcje oraz . Funkcję można przedstawić jako restrykcję funkcji do zbioru liczb rzeczywistych

dodatnich, czyli .

Podstawowe własności funkcji: okresowość,

parzystość, nieparzystość, ograniczoność,

monotoniczność

> 0

+1 x2 x( +x)x2

> 0

1 x

x > 0

= R ∖ {0} ∩

=

D

g

R

+

R

+

f

g

f g

h

x > 0

(

√ )

x

2

3

log3 1x 1 x

x ∈

D

g

: g(x) = h(x)

g h

g

h

g :

R

+

→ R, x ↦

_x1

h :

R

+

→ R, x ↦

1_x

f

x ≠ 0

f(x) =

x2+1

=

+x x3 _x1

oraz .

Liczbę nazywamy okresem funkcjiokresem funkcji. Jeżeli istnieje najmniejszy dodatnidodatni okres, to nazywamy go okresem podstawowymokresem podstawowym.

Rysunek 27: Przykłady funkcji okresowych

PRZYKŁAD

Przykład 9:

Okresem funkcji jest na przykład liczba . Jej okresem podstawowym jest liczba

PRZYKŁAD

Przykład 10:

Funkcja stała jest funkcją okresową, ale nie ma okresu podstawowego, bo każda liczba dodatnia może być jej okresem.

f : X → R

w ≠ 0

x ∈ X

x ± w ∈ X

f(x ± w) = f(x)

w

f(x) = sin x

4π

w = 2π

f(x) = c

(27)

UWAGA

Uwaga 13:

Jeżeli funkcja jest funkcja okresową o okresie , zaś , to funkcja oraz funkcja

mają ten sam okres, natomiast funkcja ma okres

Aby sporządzić wykres funkcji okresowej, wystarczy narysować go dla argumentów z dowolnego przedziału o długości , a następnie „powielić” na prawo i lewo od tego przedziału. Podobnie, aby podać funkcję okresową wystarczy zadać jej wartości w takim przedziale. Najbardziej znanymi funkcjami okresowymi są funkcje trygonometryczne. Okres podstawowy funkcji sinus i cosinus wynosi , zaś funkcji tangens i cotangens .

x ↦ f(x)

w

a ∈ R ∖ {0}

x ↦ f(x) + a

x ↦ af(x)

x ↦ f(ax)

w

|a|

w

(28)

ZADANIE

Zadanie 8:

Które z funkcji , , są okresowe ? Wskaż, o ile istnieją, ich okresy podstawowe.

1. ,

2. ,

3. .

Funkcja ma z góry zadany zbiór określoności, natomiast funkcje , będziemy rozpatrywać w ich dziedzinach naturalnych. Ad 1.

Ad 1.

Funkcja nie jest funkcja okresową, gdyż nie spełnia pierwszego warunku definicyjnego dotyczącego dziedziny. Jakkolwiek

próbowalibyśmy dobrać okres , to znajdziemy takie , że .

uwaga: gdyby funkcja ta była podana następująco to rozpatrywalibyśmy ją w jej dziedzinie naturalnej, (tzn. i oczywiście stwierdzilibyśmy, że jest to funkcja okresowa o okresie zasadniczym ).

Ad 2. Ad 2.

Dziedziną naturalną funkcji jest , gdyż wyrażenie ma sens dla dowolnej liczby rzeczywistej, więc pierwszy warunek definicyjny jest spełniony dla dowolnego . W związku z postacią funkcji (pamiętając, że funkcja

jest funkcją okresową o okresie zasadniczym ) stwierdzamy, że funkcja też jest okresowa. Jej okres zasadniczy wynosi .

Ad 3. Ad 3.

Podobnie jak dla funkcji pierwszy warunek definicyjny jest spełniony. Dalszą część zadania rozwiążemy graficznie,

korzystając z uwag dotyczących rysowania wykresów funkcji. Rysujemy etapami wykresy: , ,

Rysunek 28: Okresem zasadniczym funkcji jest

f g h

f :

R

cos 8x

w > 0

g

x ↦ cos x

2π

g

=

2π 8 π4

g

x ↦ sin x x ↦ sin x

1₂

x ↦ | sin x|.

1 2 h 2π.

(29)

UWAGA

Uwaga 14:

Funkcje okresowe znajdują zastosowanie w technice do opisu zjawisk cyklicznych, np. drgań mechanicznych i akustycznych.

DEFINICJA

Definicja 12: Parzystość i nieparzystość funkcji

Funkcję

Funkcję nazywamy parzystąparzystą wtedy i tylko wtedy, gdy dla każdego liczba oraz .

Funkcję

Funkcję nazywamy nieparzystąnieparzystą wtedy i tylko wtedy, gdy dla każdego liczba oraz

.

Rysunek 29: Funkcja parzysta. Wykres symetryczny względem osi

Rysunek 30: Funkcja nieparzysta. Wykres symetryczny względem punktu

UWAGA

Uwaga 15:

Warunek pierwszy wspólny dla funkcji parzystej i nieparzystej oznacza, że dziedzina każdej z nich powinna być symetryczna względem . W szczególności gdy , jest on trywialnie spełniony. Wykres funkcji parzystej jest symetryczny względem osi , a nieparzystej względem początku układu współrzędnych czyli punktu .

f : X → Y

x ∈ X

(−x) ∈ X

f(−x) = f(x)

f : X → Y

x ∈ X

(−x) ∈ X

f(−x) = −f(x)

0y. (0, 0)

(0, 0)

X = R

0y

(0, 0)

(30)

UWAGA

Uwaga 16:

Spośród czterech podstawowych funkcji trygonometrycznych jedynie funkcja jest parzysta, pozostałe są

nieparzyste. Inne przykładowe funkcje parzyste, to , , , , a nieparzyste , .

Zauważmy, że większość funkcji nie ma ani własności parzystości, ani nieparzystości.

ZADANIE

Zadanie 9:

Zbadajmy parzystość i nieparzystość funkcji: .

Rozwiązując nierówność mamy .

Stąd . Jest to oczywiście przedział symetryczny względem punktu , czyli warunek pierwszy jest

spełniony. Obliczmy .

Funkcja jest nieparzysta.

ZADANIE

Zadanie 10:

Zbadajmy parzystość i nieparzystość funkcji: Rozwiązanie:

Rozwiązanie:

, więc warunek dotyczący symetrii dziedziny jest spełniony. Obliczając mamy

Funkcja jest parzysta.

= {x : 5 − x ≠ 0 ∧

> 0}.

D

f 5+x5−x 5+x5−x

> 0

x ∈ (−5, 5)

= (−5, 5)

D

f

(0, 0)

f(−x)

f(−x) =

log

35−x_5+x

=

log

3

(

5+x_5−x

)

= −

= −f(x).

−1

log

35+x_5−x

f

g : x ↦ sin(cos 2x) + | sin x| + 4

= R

D

f

g(−x)

g(−x) = sin(cos(−2x)) + | sin(−x)| + 4 = sin(cos(−2x)) + | − sin x| + 4 = sin(cos 2x) + | sin x| + 4 = g(x).

g

(31)

(5) (6)

TWIERDZENIE

Twierdzenie 2: O rozkładzie funkcji na parzystą i nieparzystą

Każdą funkcję o dziedzinie symetrycznej względem punktu można przedstawić w postaci sumy dwoch funkcji ,

z których pierwsza jest parzysta, a druga nieparzysta. Wówczas , .

PRZYKŁAD

Przykład 11:

Rozłożymy funkcję na sumy części parzystej i nieparzystej.

jest zbiorem symetrycznym względem punktu , czyli taki rozkład jest możliwy. ,

. Odpowiedź

Odpowiedź

Część parzysta funkcji to funkcja kwadratowa , część nieparzysta funkcji to funkcja liniowa

PRZYKŁAD

Przykład 12:

Znajdziemy część parzystą i część nieparzystą funkcji .

jest zbiorem symetrycznym względem , czyli taki rozkład jest możliwy. ,

.

Zauważmy, że tu . Wynika to z faktu, że dana funkcja jest funkcją nieparzystą. Wówczas jej częścią parzystą jest funkcja tożsamościowo równa zeru.

Część parzysta funkcji f to funkcja , część nieparzysta funkcji to funkcja .

f

x

2

(x) =

=

= 2x

f

2 f(x)−f(−x)₂ 3 +2x+7−(3(−x −2x+7)x 2 ₎2 2 3 +2x+7−3 +2x−7x 2 _x2 2 4x2

f

(0, 0)

(x) =

=

= = 0

f

1 f(x)+f(−x)₂ 2 sin 6x+2 sin(−6x)₂ 2 sin 6x−2 sin 6x₂ 0₂

(x) =

=

= 2 sin 6x

f

2 f(x)−f(−x)₂ 2 sin 6x−2 sin(−6x)₂ 2 sin 6x+2 sin 6x₂

= f

f

2

f

(x) = 0

(32)

DEFINICJA

Definicja 13: Funkcja ograniczona z góry

Funkcja jest ograniczona z góry, jeżeli jej zbiór wartości jest ograniczony z góryograniczony z góry, czyli jeśli istnieje taka liczba , że dla każdego należacego do dziedizny funkcji

Rysunek 31: Funkcja ograniczona z góry. Wykres leży poniżej prostej

PRZYKŁAD

Przykład 13:

Funkcja jest ograniczona z góry. Jako można przyjąć liczbę lub każdą liczbę większą od . Nierówność

przyjmuje tu postać równoważną nierówności , która jest zawsze spełniona.

DEFINICJA

Definicja 14: Funkcja ograniczona z dołu

Funkcja jest ograniczona z dołu, jeżeli jej zbiór wartości jest ograniczony z dołuograniczony z dołu, czyli jeśli istnieje taka liczba ,

że dla każdego zachodzi

Rysunek 32: Funkcja ograniczona z dołu. Wykres leży nad prostą lub jej dotyka

f : X → Y

M

x

f(x) ≤ M.

y = M

f(x) = 3 − |x|

M

3

3 f(x) ≤ M

3 − |x| ≤ 3

|x| ≥ 0

f : X → Y

m

x ∈ D

f

f(x) ≥ m.

y = m

(33)

PRZYKŁAD

Przykład 14:

Funkcja jest ograniczona z dołu przez liczbę . Nierówność przyjmuje tu postać ,

czyli , co jest prawdą dla każdego .

PRZYKŁAD

Przykład 15:

Funkcja nie jest ograniczona ani z dołu, ani z góry, bo dla dowolnie dużego można wskazać takie , że

. Podobnie dla dowolnie małego można wskazać takie , że .

DEFINICJA

Definicja 15: Funkcja ograniczona

Funkcja

Funkcja jest ograniczonaograniczona, jeśli jest ona ograniczona zarówno z góry jak i z dołu.

Rysunek 33: Funkcja ograniczona. Wykres leży pomiedzy prostymi oraz

PRZYKŁAD

Przykład 16:

Funkcja jest ograniczona z góry przez liczbę i z dołu przez liczbę , czyli jest funkcją ograniczoną.

f(x) =

2

x

− 1

₋₁

_{f(x) ≥ m}

₂

x

_{− 1 ≥ −1}

≥ 0

2

x

_{x ∈ R.}

f(x) = x

3

_M

_x

> M

x

3

_m

_x

3

_{< m}

f : X → F

y = M y = −M

f(x) = 2 + cos x

3

1

(34)

DEFINICJA

Definicja 16: Funkcja rosnąca

Funkcja

Funkcja jest rosnąca w zbiorze rosnąca w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że .

Rysunek 34: Przykład funkcji rosnącej

DEFINICJA

Definicja 17: Funkcja słabo rosnąca

Funkcja

Funkcja jest słabo rosnąca (niemalejąca) w zbiorze słabo rosnąca (niemalejąca) w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że

Rysunek 35: Przykład funkcji słabo rosnącej

f

A ⊂ D

f

x

1

, ∈ A

x

2

x

1

<

x

2

Funkcja

Funkcja jest malejąca w zbiorze malejąca w zbiorze , jeśli dla każdych dwóch elementów stąd, że wynika, że

Rysunek 36: Przykład funkcji malejącej

DEFINICJA

Definicja 19: Funkcja słabo malejąca

1

x

2

f( ) ≥ f( )

x

1

x

2

(36)

Rysunek 37: Przykład funkcji słabo malejącej

UWAGA

Uwaga 18:

Funkcja malejąca to taka funkcja, dla której wraz ze wzrostem argumentu maleje wartość funkcji. Wykres funkcji malejącej "opada w dół" od lewej do prawej.

DEFINICJA

Definicja 20: Funkcja monotoniczna

Funkcja monotoniczna w zbiorze

Funkcja monotoniczna w zbiorze to funkcja, która jest słabo rosnąca na lub słabo malejąca na .

Funkcję

Funkcję nazywamy ściśle monotoniczną w ściśle monotoniczną w , jeśli jest ona rosnąca lub malejąca.

UWAGA

Uwaga 19:

Monotoniczność funkcji ma duże znaczenie podczas rozwiązywania nierówności. Obrazowo można powiedzieć, że funkcje rosnące nie zmieniają zwrotu nierówności, natomiast funkcje malejące zmieniają ten zwrot.

Funkcje logartymiczne i wykładnicze o podstawie ułamkowej z przedziału są malejące, stąd zmiana zwrotu podczas "opuszczania" symbolu tych funkcji, np:

Rozwiązując nierówność:

pamiętamy, że funkcja jest malejąca i zmieniamy zwrot znaku nierówności przy "opuszczaniu logarytmu otrzymując nierówność kwadratową".

A ⊂ D

f

A

(0, 1)

(3x + 2) ≤

,

log

1 2

log

12

x

2

x ↦

log

1

x

2

3x + 2 ≥ x

2

(37)

Natomiast podczas rozwiązywania nierówności:

wiedząc, że funkcja jest rosnąca pozostawiamy niezmieniony zwrot nierówności otrzymując

wówczas nierówność kwadratową

Algebraiczne działania na funkcjach

DEFINICJA

Definicja 21: Suma, różnica, iloczyn i iloraz funkcji

Niech będą dane dwie funkcje ,

Sumą funkcji

Sumą funkcji i i nazywamy funkcję

taką, że , dla każdego .

Różnicą funkcji

Różnicą funkcji i i nazywamy funkcję

Iloczynem funkcji

Iloczynem funkcji i i nazywamy funkcję

Jeżeli ponadto dla każdego to ilorazem funkcji ilorazem funkcji i i nazywamy funkcję

taką, że dla każdego

TWIERDZENIE

Twierdzenie 3: Działania arytmetyczne na funkcjach a własności funkcji

Suma funkcji ograniczonych jest funkcją ograniczoną. Iloczyn funkcji ograniczonych jest funkcją ograniczoną. Suma funkcji rosnących jest funkcją rosnącą.

Iloczyn nieujemnych funkcji rosnących jest funkcją rosnącą. Suma funkcji malejących jest funkcją malejącą.

Iloczyn nieujemnych funkcji malejących jest funkcją malejącą.

Suma funkcji słabo rosnących jest funkcją słabo rosnącą. Iloczyn nieujemnych funkcji słabo rosnących jest funkcją słabo rosnącą.

Suma funkcji słabo malejących jest funkcją słabo malejącą. Iloczyn nieujemnych funkcji słabo malejących jest funkcją słabo malejącą.

Identyczność

(3x + 2) ≤

,

log

2

log

2

x

2

x ↦ lo x

g

2

3x + 2 ≤ ,

x

2

f : X → R g : X → R

f g

(f + g) : X → R

(f + g)(x) = f(x) + g(x)

x ∈ X

f g

(f − g) : X → R

(f − g)(x) = f(x) − g(x)

x ∈ X

f g

(f ⋅ g) : X → R

(f ⋅ g)(x) = f(x) ⋅ g(x)

x ∈ X

g(x) ≠ 0

x ∈ X

f g

: X → R

f g fg

(x) =

f(x)g(x)

x ∈ X

(38)

DEFINICJA

Definicja 22: Funkcja identycznościowa

Funkcją identycznościową w zbiorze

Funkcją identycznościową w zbiorze (identycznością w zbiorze ) nazywamy funkcję określoną wzorem

, dla każdego .

Funkcję identycznościową w zbiorze oznaczamy symbolem . Mamy więc , , dla każdego

UWAGA

Uwaga 20:

Wykres funkcji identycznościowej leży zawsze na diagonali, czyli prostej o równaniu będącej dwusieczną pierwszej i trzeciej ćwiartki układu współrzędnych.

Rysunek 38: Wykres funkcji identycznościowej na przedziale domkniętym

Składanie funkcji

DEFINICJA

Definicja 23: Złożenie funkcji

Złożeniem funkcji

Złożeniem funkcji i i , gdzie nazywamy funkcję oznaczoną , określoną następująco

, , dla każdego .

Funkcję nazywamy wówczas funkcją wewnętrznąfunkcją wewnętrzną, a funkcję funkcja zewnętrzną.funkcja zewnętrzną.

A

f : A → A

f(x) = x

x ∈ A

A

id

A

i : A → A

d

A

i (x) = x

d

A

x ∈ A

y = x

[−1, 1]

f : X → Y g : Z → W

Y ⊂ Z

g ∘ f

g ∘ f : X → W (g ∘ f)(x) = g(f(x))

x ∈ X

f

g

(39)

Rysunek 39: Ilustracja złożenia funkcji

PRZYKŁAD

Przykład 17:

Dane są funkcje: Utworzymy złożenia , , Rozwiązanie Rozwiązanie

W naszym przykładzie wszystkie zbiory występujące w definicji złożenia są równe .

Obliczamy

Mamy, więc

UWAGA

Uwaga 21:

Jak widać z powyższego przykładu, składanie funkcji jest operacją nieprzemiennąoperacją nieprzemienną.

f : R → R, f(x) = x + 1,

g : →R, g(x) = 3 + 2x

x

2

g ∘ f f ∘ g f ∘ f

X = Y = Z = W = R

(g ∘ f)(x) = g(f(x)) = g(x + 1) = 3(x + 1 + 2(x + 1) = 3 + 8x + 5,

)

2

_x

2

(f ∘ g)(x) = f(g(x)) = f(3 + 2x) = 3 + 2x + 1,

x

2

_x

2

(f ∘ f)(x) = f(f(x)) = f(x + 1) = x + 1 + 1 = x + 2.

g ∘ f : R → R, (g ∘ f)(x) = 3 + 8x + 5,

x

2

f ∘ g : R → R, (f ∘ g)(x) = 3 + 2x + 1,

x

2

f ∘ f : R → R, (f ∘ f)(x) = x + 2.

(40)

UWAGA

Uwaga 22: Warunek złożenia funkcji

Jeżeli funkcja oraz podane są jedynie za pomocą wzorów, to jest możliwe ich złożenie , jeśli tylko niepusty jest

zbiór . Zbiór ten jest wówczas dziedziną (naturalną) złożenia.

ZADANIE

Zadanie 11:

Niech , . Utworzymy złożenie , podając ich wzory i dziedziny.

Rozwiązanie: Rozwiązanie: Mamy więc Odpowiedź Odpowiedź

f

g

g ∘ f

{x ∈ R : x ∈

D

f

i f(x) ∈

D

g

}

f(x) = log x g(x) = 3x + 5

f ∘ g

(f ∘ g)(x) = f(g(x)) = f(3x + 5) = log(3x + 5),

= {x ∈ R : x ∈

i g(x) ∈

},

f∘g

= ( , +∞).

−53

(41)

ZADANIE

Zadanie 12:

Rozwiązanie: Rozwiązanie: Mamy więc . Odpowiedź Odpowiedź

ZADANIE

Zadanie 13:

Mamy więc i . Rozwiązując ostatnią nierówność otrzymujemy , czyli (korzystamy z

faktu, że funkcja logarytmiczna jest rosnąca, gdyż tu podstawa logarytmu równa się czyli jest większa od

jedynki). Odpowiedź Odpowiedź

TWIERDZENIE

Twierdzenie 4: O monotoniczności złożeń

Złożenie dwóch funkcji rosnących jest funkcją rosnącą. Złożenie dwóch funkcji malejących jest funkcją rosnącą.

Złożenie funkcji rosnącej i malejącej w dowolnej kolejności jest funkcją malejącą.

f(x) = log x g(x) = 3x + 5

g ∘ f

(g ∘ f)(x) = g(f(x)) = g(log x) = 3 log x + 5,

= {x ∈ R : x ∈

i f(x) ∈

},

= (0, ∞)

f(x) = log x g(x) = 3x + 5

f ∘ f

(f ∘ f)(x) = f(f(x)) = f(log x) = log(log x),

= {x ∈ R : x ∈

i f(x) ∈

}.

(42)

PRZYKŁAD

Przykład 18:

Zbadamy monotoniczność danej funkcji i określimy rodzaj jej monotoniczności.

Pokażemy, że funkcja jest funkcją rosnącą.

Funkcję potraktujemy jako funkcję złożoną z trzech funkcji . Kładziemy:

, ,

Sprawdzimy, czy dobrze określiliśmy funkcje składowe.

Z łatwością określamy monotoniczność funkcji składowych. Funkcja jest funkcją malejącą, jest funkcją rosnącą, zatem ich złożenie jest funkcją malejącą. Funkcja jest funkcją malejącą jako funkcja wykładnicza o podstawie z

przedziału więc jej złożenie z funkcją malejącą jest funkcją rosnącą. A to złożenie jest badaną funkcją .

Funkcja jest rosnąca.

Pojęcie funkcji odwrotnej do danej

f(x) = ( )

1 3 2(1−x)5

f

f = ∘ ∘

f

3

f

2

f

1

(x) = 1 − x

f

1

(x) = 2

f

2

f

1

f

3

(0, 1)

f

2

∘

f

1

∘ ( ∘ ) = ∘ ∘

Niech funkcja będzie bijekcją (funkcją różnowartościową (iniekcjąiniekcją) i „na” (suriekcjąsuriekcją). Funkcją odwrotną doFunkcją odwrotną do funkcji

funkcji nazywamy funkcję spełniającą warunek:

Rysunek 40: Dziedziną funkcji jest przeciwdziedzina funkcji , a przeciwdziedziną funkcji jest dziedzina funkcji