Podciąg i WKW zbieżności ciągu

(1)

Podciąg i WKW zbieżności

ciągu

Autorzy:

Katarzyna Czyżewska

(2)

Podciąg i WKW zbieżności ciągu

Autor: Katarzyna Czyżewska

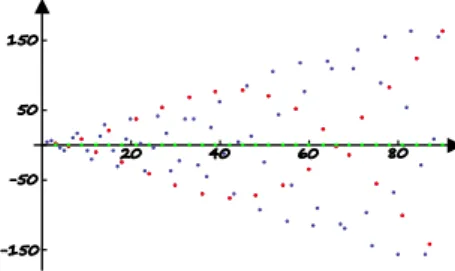
Rys. 1 przedstawia wykres ciągu o dziedzinie (niebieski), z którego zostały wybrane tylko pewne wyrazy (poprawione na czerwono). Indeksy tych wyrazów zostały zaznaczone na osi odciętych (zielone) i są to pewne liczby naturalne tworzące ciąg liczb naturalnych .

Rysunek 1: Interpretacja geometryczna podciągu

Komentarz Komentarz

Nieskończenie wiele, ale nie wszystkie, wyrazy starego ciągu tworzą więc nowy ciąg indeksowany liczbami , które zachowują porządek liczb naturalnych, tzn. jeżeli , to . Czyli na bazie ciągu starego powstaje nowy ciąg

nieskończony, którego dziedzina jest podzbiorem zbioru . Taki nowy ciąg nazywamy podciągiem ciągu starego. Oczywiste jest, że mamy nieskończenie wiele możliwości utworzenia z ciągu bazowego różnych jego podciągów np. poprzez odrzucenie pewnej skończonej liczby wyrazów ciągu, poprzez wybranie wyrazów o indeksach będących wielokrotnością pewnej liczby naturalnej itp.

DEFINICJA

Definicja 1: Podciąg

Nieskończonym podciągiem ciągu nazywamy funkcję , gdzie i zbiór jest nieskończony.

UWAGA

Uwaga 1: Oznaczenie nieskończonego podciąg ciągu

Nieskończony podciąg ciągu oznaczamy przez , gdzie i dla każdego zachodzą warunki oraz

Rysunek 2: Interpretacja geometryczna granicy podciągu

Rys. 2 przedstawia ciąg zbieżny do granicy (niebieski) i wybrany z niego podciąg (czerwony). Z definicji granicy wiemy, że dla dowolnego prawie wszystkie wyrazy ciągu leżą w przedziale , a ponieważ wyrazy podciągu są jednocześnie

N

( )

n

k

( )

a

n

( )

a

nk

n

k

k < l

n

k

<

n

l

N

= a(n), n ∈ N

a

n

a: A → R

A ⊂ N

A

( )

a

n

( )

a

nk

a

nk

= a( )

n

k

k ∈ N

∈ A

n

k

n

1

<

n

2

< ⋯

3 ϵ > 0

(3 − ϵ, 3 + ϵ)

(3)

wyrazami naszego ciągu, prawie wszystkie wyrazy podciągu też leżą w tym przedziale. Czyli możemy wnioskować, że dla ciągu zbieżnego, wszystkie jego podciągi są zbieżne do tej samej granicy, co wyjściowy ciąg. Rozumowanie to działa też w drugą stronę, gdyż przy założeniu, że wszystkie podciągi badanego ciągu są zbieżne do tej samej granicy, a jednym z podciągów jest np. wyjściowy ciąg bez kilku początkowych wyrazów, więc wyjściowy ciąg też jest zbieżny do tej samej granicy, gdyż skończona liczba początkowych wyrazów nie ma wpływu na zbieżność ciągu.

TWIERDZENIE

Twierdzenie 1: Warunek konieczny i wystarczający (WKW) zbieżności ciągu

Ciąg ma granicę właściwą wtedy i tylko wtedy, gdy każdy nieskończony podciąg ciągu ma granicę .

UWAGA

Uwaga 2:

Warunek konieczny i wystarczający działa w dwie strony, tzn. jeżeli ciąg jest zbieżny do granicy , to każdy

nieskończony podciąg ciągu jest zbieżny do tej samej granicy i na odwrót jeżeli każdy nieskończony podciąg ciągu jest zbieżny do tej samej granicy , to ciąg tez jest zbieżny do granicy .

Od razu widać mankamenty, ale też zalety tego twierdzenia. Wprawdzie wykazanie za pomocą WKW, że jakiś ciąg jest zbieżny, jest dość trudne, bo musielibyśmy znaleźć wszystkie możliwe podciągi naszego ciągu i pokazać, że mają takie same granice, ale wykazanie, że ciąg jest rozbieżny jest za to bardzo proste. Wystarczy znaleźć jakiekolwiek dwa podciągi, które mają różne granice i wtedy na podstawie WKW wiadomo, że ciąg nie jest zbieżny.

PRZYKŁAD

Przykład 1:

Zbadaj zbieżność ciągu Rozwiązanie:

Rozważmy dwa różne podciągi ciągu

dla mamy , czyli

Zatem znaleźliśmy dwa podciągi ciągu , które maja różne granice, czyli ciąg jest rozbieżny (nie ma granicy).

( )

a

n

a

( )

a

nk

( )

a

n

a

( )

a

n

a

( )

a

nk

( )

a

n

a

( )

a

nk

( )

a

n

a

( )

a

n

a

= sin

a

n nπ₂

( )

a

n

= 2k

n

k

a

nk

= sin

2kπ₂

= sin kπ = 0

lim

k→∞

a

2k

=

lim

k→∞

0 = 0

= 4k + 1

n

k

a

nk

= sin

4kπ+π2

= sin (2kπ + ) = 1

π2

lim

k→∞

a

4k+1

= 1

(4)

PRZYKŁAD

Przykład 2:

Rozważmy różne podciągi ciągu , czyli

, czyli , czyli

Znaleźliśmy trzy podciągi ciągu , które mają różne granice, a zatem ciąg jest rozbieżny.

PRZYKŁAD

Przykład 3:

Rozważymy dwa różne podciągi ciągu

granicę ciągu obliczymy korzystając z twierdzenia o trzech ciągach czyli

granice ciągu obliczymy korzystając z twierdzenia o trzech ciągach czyli

Zatem znaleźliśmy dwa podciągi ciągu , które mają różne granice, czyli ciąg jest rozbieżny.

WNIOSEK

Wniosek 1:

Jeżeli i ciągi nie są ciągami stałymi, to nie istnieją granice tych ciągów.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

= tan

b

n nπ₃

( )

b

n

= tan

= tan kπ = 0

b

3k 3kπ₃

lim

k→∞

b

3k

= 0

= tan

= tan (kπ − ) = tan (− ) = tan ( ) =

b

3k−2 (3k−2)π₃ 2π₃ 2π₃ ₃π

√

3 lim

k→∞

b

3k−2

=

√

3 = tan

= tan (kπ − ) = tan (− ) = −

b

3k−1 (3k−1)π3 π3 π3

√

3 lim

k→∞

b

3k−1

= −

√

3 ( )

b

n

( )

b

n

=

c

n

2

n cos (nπ)

+

3

2n(−1)n+1

−

−−−−−−−−−−−−−−

−

√

n

( )

c

n

=

c

2k

√

2k

−

2 −−−−−−−

2k

+

3

−2⋅2k

−

2

2k

+

( )

19 2k

−

−−−−−−−

−

√

2k

( )

c

2k

2 =

_√

2k

−−

2 −

2k

≤

= 2

2 +

2

2k

_{( )}

1 9 2k

−

−−−−−−−

−

√

2k

√

2k

₂

−

−−−−−

_2k

₊

₂

_2k

−

2k

_√

₂

k→∞

_⟶

= 2

lim

k→∞

c

2k

=

c

2k−1 2k−1

√

−

2 −−−−−−−−−−−−−−

(2k−1)⋅(−1)

+

3

2⋅(2k−1)

−

( )

1₂ 2k−1

+

9

2k−1

−

−−−−−−−−−−

−

√

2k−1

(

c

2k−1

)

9 =

2k−1

_√

9 − −

−−

2k−1

≤

_{( )}

₁

₊

≤

= 9

9

2 2k−1

9

2k−1

−

−−−−−−−−−−

−

√

2k−1 2k−1

√

−

₉

−−−−−−−−

_2k−1

₊

₉

_2k−1

−

2k−1

_√

₂

k→∞

_⟶

= 9

lim

k→∞

c

2k−1

( )

c

n

( )

c

n

= ±∞

(5)

Data generacji dokumentu: 2019-04-15 05:08:27

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=88c91be2f4fdd3acc29ef1a56bb01c09