Zastosowanie pochodnej. Twierdzenie Rolle'a i Lagrange'a. Pochodna a monotoniczność funkcji

(1)

Zastosowanie pochodnej.

Twierdzenie Rolle'a i

Lagrange'a. Pochodna a

monotoniczność funkcji

Autorzy:

Tomasz Zabawa

2019

(2)

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: Rolle'a

Rolle'a

Jeżeli

1. funkcja jest ciągła w przedziale ,

2. funkcja ma pochodną właściwą lub niewłaściwą w przedziale ,

3. ,

to

istnieje takie, że .

UWAGA

Uwaga 1:

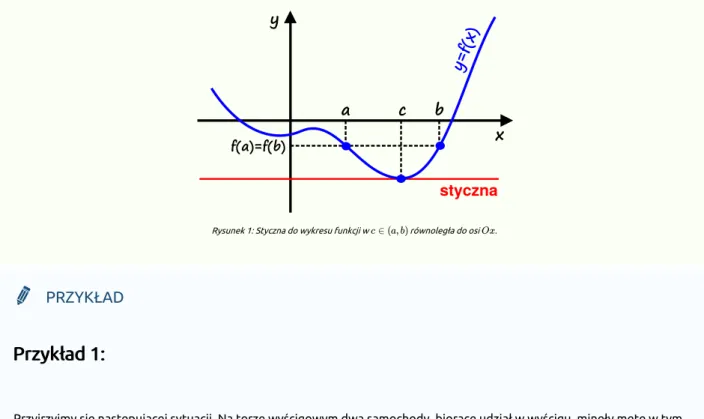
Przyjrzyjmy się interpretacji geometrycznej . Zerowanie się pochodnej funkcji w punkcie oznacza, że styczna do wykresu funkcji w tym punkcie jest pozioma. Jeżeli są spełnione założenia , to istnieje punkt , w którym styczna do wykresu funkcji jest równoległa do osi .

styczna

Rysunek 1: Styczna do wykresu funkcji w równoległa do osi .

PRZYKŁAD

Przykład 1:

Przyjrzyjmy się następującej sytuacji. Na torze wyścigowym dwa samochody, biorące udział w wyścigu, minęły metę w tym samym momencie. Na podstawie możemy wywnioskować, że w czasie wyścigu był moment, w którym samochody jechały z dokładnie taką samą prędkością. Dlaczego? Jeżeli rozpatrzymy funkcję, która danemu czasowi przypisuje różnicę przebytej drogi przez samochody w tym czasie, to zauważmy, że ta funkcja spełnia założenia . Zatem dla pewnego momentu czasu pochodna tej funkcji jest równa zero, a pochodna tej funkcji będzie równa różnicy prędkości samochodów.

f

[a, b]

f

(a, b)

f(a) = f(b)

c ∈ (a, b)

f

′

(c) = 0

c ∈ (a, b)

f

Ox

c ∈ (a, b) Ox

(3)

PRZYKŁAD

Przykład 2:

Niech wielomian ma 101 różnych pierwiastków rzeczywistych. Korzystając z możemy wykazać, że setna pochodna wielomianu ma co najmniej jeden pierwiastek rzeczywisty. Z otrzymujemy, że między każdymi dwoma pierwiastkami wielomianu istnieje argument będący pierwiastkiem , zatem widzimy, że ma 100 różnych pierwiastków rzeczywistych. Postępując analogicznie dla kolejnych pochodnych otrzymujemy, że istnieje punkt , w którym

.

TWIERDZENIE

Twierdzenie 2:

Twierdzenie 2: Lagrange'a

Lagrange'a

Jeżeli

1. funkcja jest ciągła w przedziale ,

2. funkcja ma pochodną właściwą lub niewłaściwą w przedziale , to

istnieje takie, że .

UWAGA

Uwaga 2:

jest prostym wnioskiem z , zatem twierdzenie Lagrange'a jest uogólnieniem twierdzenia Rolle'a.

W

′

_W

′

c ∈ R

(c) = 0

W

(100)

f

[a, b]

f

(a, b)

c ∈ (a, b)

f

′

(c) =

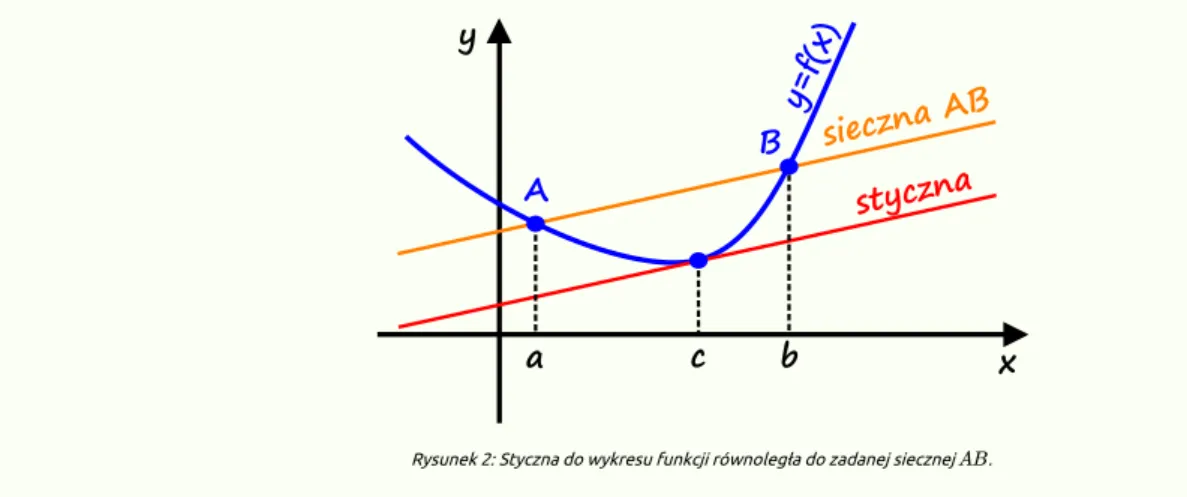
f(b)−f(a) b−a

(4)

Interpretacją geometryczną jest wniosek, że jeżeli funkcja spełnia założenia , to istnieje styczna do wykresu funkcji w punkcie równoległa do siecznej wykresu funkcji przecinającej go w punktach i .

Rysunek 2: Styczna do wykresu funkcji równoległa do zadanej siecznej .

Przejdźmy teraz do wspomnianego twierdzenia łączącego znak pochodnej funkcji z monotonicznością funkcji. Twierdzenie to pozwala badanie monotoniczności funkcji sprowadzić do rozwiązania nierówności.

TWIERDZENIE

Twierdzenie 3:

Twierdzenie 3: o związku znaku pochodnej funkcji z monotonicznością funkcji

o związku znaku pochodnej funkcji z monotonicznością funkcji

Niech oznacza dowolny przedział.

1. Jeżeli dla każdego , to funkcja jest stała w przedziale . 2. Jeżeli dla każdego , to funkcja jest rosnąca w przedziale . 3. Jeżeli dla każdego , to funkcja jest malejąca w przedziale . 4. Jeżeli dla każdego , to funkcja jest niemalejąca w przedziale . 5. Jeżeli dla każdego , to funkcja jest nierosnąca w przedziale .

UWAGA

Uwaga 4:

Założenie, że jest przedziałem, jest bardzo istotne. jest prawdziwe, gdy stosujemy je w przedziale. Natomiast w zbiorze będącym sumą rozłącznych przedziałów, już nie zawsze jest prawdziwe.

f

c ∈ (a, b)

f

A(a, f(a)) B(b, f(b))

AB

I

(x) = 0

f

′

_{x ∈ I}

_f

_I

(x) > 0

f

′

_{x ∈ I}

_f

_I

(x) < 0

f

′

_{x ∈ I}

_f

_I

(x) ≥ 0

f

′

_{x ∈ I}

_f

_I

(x) ≤ 0

f

′

_{x ∈ I}

_f

_I

I

(5)

PRZYKŁAD

Przykład 3:

Weźmy dla przykładu funkcję , której pochodna jest mniejsza od zera dla każdego

. Funkcja jest malejąca w przedziale i funkcja jest malejąca w przedziale . Natomiast fałszywe jest stwierdzenie, że funkcja jest malejąca w .

UWAGA

Uwaga 5:

Jeżeli dla każdego i tylko w skończonej liczbie punktówtylko w skończonej liczbie punktów przedziału , to funkcja jest rosnąca w przedziale .

Analogicznie: Jeżeli dla każdego i tylko w skończonej liczbie punktówtylko w skończonej liczbie punktów przedziału , to funkcja jest malejąca w przedziale .

PRZYKŁAD

Przykład 4:

Przyjrzyjmy się pochodnej i monotoniczności funkcji . Pochodna funkcji to , zatem dla każdego oraz . Z wiemy, że funkcja jest rosnąca w przedziale i że funkcja jest rosnąca w przedziale . Ale wykorzystując możemy stwierdzić, że funkcja jest rosnąca w całym zbiorze liczb rzeczywistych, bo

dla każdego i jest równa zero dla tylko jednego argumentu (czyli dla skończonej liczby argumentów). Ten wniosek zgadza się z naszą wiedzą o funkcji .

f(x) =

1 x

f

′

(x) = −

x12

x ∈

D

f

= (−∞, 0) ∪ (0, +∞)

f

(−∞, 0)

f

(0, +∞)

f(x) =

1 x

(−∞, 0) ∪ (0, +∞)

(x) ≥ 0

f

′

_{x ∈ I}

_f

′

_{(x) = 0}

_I

_f

I

(x) ≤ 0

f

′

_{x ∈ I}

_f

′

_{(x) = 0}

_I

_f

I

f(x) = x

3

_f

′

_{(x) = 3}

_x

2

_f

′

_{(x) > 0}

x ≠ 0

f

′

(0) = 0

_f

_{(−∞, 0)}

_f

(0, +∞)

(x) ≥ 0

f

′

_{x ∈ R}

f(x) = x

3

(6)

Zbadajmy monotoniczność funkcji

Rozpoczynamy badanie monotoniczności funkcji od określenia dziedziny funkcji : Obliczamy pochodną funkcji :

Aby określić monotoniczność funkcji , potrzebujemy rozwiązać nierówności: oraz . Zauważmy, że znak pochodnej nie będzie zależał od mianownika, ponieważ dla każdego . Zatem

Z tego faktu na podstawie wnioskujemy, że:

funkcja jest rosnąca w przedziale , funkcja jest rosnąca w przedziale . Przejdźmy do drugiej nierówności:

I tu na podstawie wnioskujemy, że:

funkcja jest malejąca w przedziale , funkcja jest malejąca w przedziale , funkcja jest malejąca w przedziale , funkcja jest malejąca w przedziale .

Zwróćmy uwagę, że nieprawdą jest, że funkcja jest malejąca w zbiorze czy . Jedynie na podstawie możemy stwierdzić, że funkcja jest malejąca w przedziale , bo i dla

każdego .

Następne dwa twierdzenia pokażą nam, że porównanie wartości pochodnych dwóch funkcji w pewnym przedziale oraz porównanie wartości tych funkcji w pewnym punkcie tego przedziału, pozwala wnioskować o relacji tych funkcji w rozważanym przedziale.

TWIERDZENIE

Twierdzenie 4:

Twierdzenie 4: o równości funkcji

o równości funkcji

Niech funkcje i będą określone w przedziale oraz . Jeżeli i dla każdego , to dla każdego .

f(x) =

x3

.

−4 x2

f

= (−∞, −2) ∪ (−2, 2) ∪ (2, +∞).

D

f

(x) =

=

.

f

′ 3 ( −4)− 2xx2_x2 _x3 ( −4x2 ₎2 x−12 4 _x2 ( −4x2 ₎2

f

′

(x) > 0

_f

′

_{(x) < 0}

( − 4 > 0

x

2

₎

2

_{x ∈ D}

f

(x) > 0 ⇔

f

′

⇔

− 12 > 0 ∧ x ∈

⇔

x

4

_x

2

_D

f

(x + 2 )(x − 2 ) > 0 ∧ x ∈

⇔

x

2

_√

₃

_√

₃

_D

f

x ∈ [(−∞, −2 ) ∪ (2 , +∞)] ∩

√

3 √

3 D

f

⇔

x ∈ (−∞, −2 ) ∪ (2 , +∞).

√

3 √

3 f

(−∞, −2 )

√

3 f

(2 , +∞)

√

3 (x) < 0 ⇔

f

′

⇔

− 12 < 0 ∧ x ∈

⇔

x

4

_x

2

_D

f

(x + 2 )(x − 2 ) < 0 ∧ x ∈

⇔

x

2

_√

₃

_√

₃

_D

f

x ∈ [(−2 , 0) ∪ (0, 2 )] ∩

√

3 √

3 D

f

⇔

x ∈ (−2 , −2) ∪ (−2, 0) ∪ (0, 2) ∪ (2, 2 )

√

3 √

3 f

(−2 , −2)

√

3 f

(−2, 0)

f

(0, 2)

f

(2, 2 )

√

3 f

(−2 , −2) ∪ (−2, 0)

√

3 (0, 2) ∪ (2, 2 )

√

3 f

(−2, 2)

f

′

(0) = 0

_f

′

_{(x) < 0}

x ∈ (−2, 0) ∪ (0, 2)

f g

I

x

0

∈ I

f( ) = g( )

x

0

x

0

f

′

(x) = (x)

g

′

x ∈ I

f(x) = g(x)

x ∈ I

(7)

TWIERDZENIE

Twierdzenie 5:

Twierdzenie 5: o nierówności funkcji

o nierówności funkcji

Niech funkcje i będą ciągłe w przedziale oraz .

Jeżeli i dla każdego takiego, że jest spełniona nierówność , to dla każdego takiego, że .

UWAGA

Uwaga 6:

Pochodna funkcji opisuje, jak zmienia się funkcja. Analizując powyższe twierdzenia widać, że pochodna nie tylko opisuje czy funkcja jest rosnąca czy malejąca, ale również tempo tych zmian. Funkcja rosnąca o większej pochodnej rośnie szybciej niż funkcja rosnąca mająca mniejszą pochodną (dodatnią). Funkcje o równych pochodnych zmieniają się w tym samym tempie.

PRZYKŁAD

Przykład 6:

Korzystając z , wykażemy prawdziwość wzoru

Rozważmy następujące funkcje i . Pochodne tych funkcji dla wynoszą:

czyli są sobie równe. Zauważmy również, że wartości tych funkcji w zerze są sobie równe:

Zatem na podstawie wnioskujemy, że czyli

Uwzględniając fakt, że , , i , otrzymujemy wzór:

Postępując analogicznie można wykazać również wzór:

Powyższe twierdzenia znajdują zastosowanie również w rozwiązywaniu równań i nierówności nieelementarnych.

f g

I

x

0

∈ I

f( ) ≤ g( )

x

0

x

0

x ∈ I

x > x

0

f

′

(x) ≤ (x)

g

′

f(x) ≤ g(x)

x ∈ I

x ≥ x

0

arcsinx + arccosx =

π

dla ka

ż

dego x ∈ (−1, 1).

2

f(x) = arcsin x g(x) = − arccosx

π 2

x ∈ (−1, 1)

(x) =

f

′

(x) =

g

′

,

1 1 − x

2

− −

−−−

√

,

1 1 − x

2

− −

−−−

√

f(0) =

g(0) =

arcsin0 = 0,

− arccos0 = − = 0.

π

2 π

2 arcsinx = − arccosx dla ka

π ż

dego x ∈ (−1, 1),

2

arcsinx + arccosx =

π₂

dla ka

ż

dego x ∈ (−1, 1).

arcsin(−1) = −

π

2

arccos(−1) = π arcsin1 =

π2

arccos1 = 0

arcsinx + arccosx =

π

dla ka

ż

dego x ∈ [−1, 1].

2

arctgx + arcctgx =

π

dla ka

ż

dego x ∈ R.

2

(8)

Rozwiążmy równanie

Określmy dziedzinę tego równania: . Podejrzewamy, że powyższe równanie nie ma rozwiązania, ale jak to wykazać? Dla każdego wiemy, że i , zatem dla każdego . Rozważmy teraz przedział . Niech i . Są to funkcje ciągłe w przedziale , a ponadto dla tych funkcji mamy:

Funkcje i w przedziale spełniają założenia , zatem korzystając z otrzymujemy:

czyli . Oczywiście , zatem dla każdego . Wykazaliśmy, że dla każdego , co oznacza, że równanie nie ma rozwiązania.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 06:16:31

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=4fa99463b149ddc4472a6fdf4fc886ad

Autor: Tomasz Zabawa

= ln x.

x

3

D = (0, +∞)

x ∈ (0, 1)

ln x < 0 0 < x

3

_{ln x < x}

3

_{x ∈ (0, 1)}

[1, +∞)

f(x) = 1 + ln x g(x) = x

3

_{[1, +∞)}

f(1) = 1 i g(1) = 1

(x) =

f

′

1 _x

(x) = 3

g

′

_x

2

< 3 dla x ∈ [1, +∞)

1 x

x

2

⇒ f(1) ≤ g(1)

⇒ (x) ≤ (x)

f

′

_g

′

f g

[1, +∞)

f(x) ≤ g(x) dla ka

ż

dego x ∈ [1, +∞),

1 + ln x ≤ x

3

_{ln x < 1 + ln x}

_{ln x < x}

3

_{x ∈ [1, +∞)}

_{ln x < x}

3

x ∈ D

x

3

= ln x