Definicja granicy funkcji w punkcie i w nieskończoności

(1)

Definicja granicy funkcji w

punkcie i w nieskończoności

Autorzy:

Katarzyna Czyżewska

(2)

Definicja granicy funkcji w punkcie i w nieskończoności

Autor: Katarzyna Czyżewska

DEFINICJA

Definicja 1: Otoczenie i sąsiedztwo punktu

Otoczeniem punktu nazywamy dowolny przedział otwarty zawierający ten punkt, tzn. , a sąsiedztwem punktu nazywamy otoczenie z wyłączeniem punktu .

Oznaczenia Oznaczenia

Otoczenie punktu oznaczamy symbolicznie , a sąsiedztwo punktu oznaczamy przez .

Komentarz Komentarz

W wielu sytuacjach, przy badaniu własności funkcji , gdzie interesuje nas tylko jej zachowanie w bliskim sąsiedztwie punktu w którym funkcja nie musi być określona. Zawężamy wtedy funkcję do otoczenia lub sąsiedztwa punktu , zamiast zajmować się całą dziedziną funkcji. Jeżeli funkcja posiada pewną własność w otoczeniu lub sąsiedztwie, które może być nawet bardzo małe, punktu , to mówimy o lokalnym zachowaniu się funkcji. Pojęcie granicy funkcji w punkcie należy właśnie do takiej kategorii własności.

DEFINICJA

Definicja 2: Definicja Cauchy'ego granicy właściwej funkcji w punkcie

Mówimy, że funkcja ma granicę w punkcie , gdzie pewne sąsiedztwo jest zawarte w dziedzinie funkcji, jeżeli dla dowolnego otoczenia punktu da się dobrać sąsiedztwo punktu tak, aby dla wszystkich argumentów z tego sąsiedztwa, wartości funkcji dla tych argumentów wpadały do otoczenia punktu .

Oznaczenia Oznaczenia

Granicę funkcji w punkcie oznaczamy przez

UWAGA

Uwaga 1:

Definicję Cauchy’ego granicy właściwej funkcji w punkcie można zapisać symbolicznie: funkcja ma w punkcie granicę równą wtedy i tylko wtedy, gdy

.

∈ R

x

0

(a, b)

x

0

∈ (a, b)

∈ R

x

0

x

0

∈ R

x

0

R

(3)

ε f(x) x g +

}

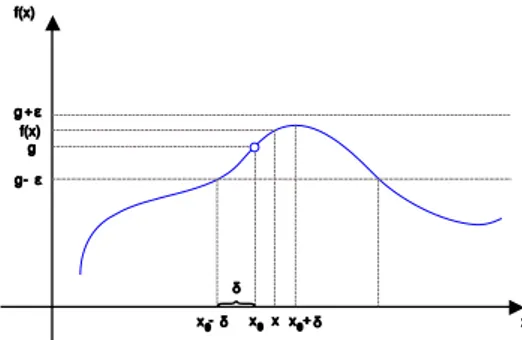
x0 x f(x) δ x0+ δ x0 -δ ε g-g

Rysunek 1: Interpretacja geometryczna definicji Cauchy'ego granicy funkcji w punkcie

Na Rys. 1 widzimy wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w

sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest granicą funkcji w punkcie . W tym celu bierzemy dowolne i wyznaczamy przedział , który przedłużamy do pasa wzdłuż osi odciętych. Wyznaczamy punkty przecięcia prostych i z wykresem funkcji , które rzutujemy prostopadle na oś odciętych. Przez oznaczymy najmniejszą z odległości zrzutowanych punktów od punktu . Pokazujemy, że dla dowolnego argumentu należącego do przedziału wartość funkcji dla tego argumentu wpada do przedziału

, co spełnia warunki definicji Cauchy’ego granicy funkcji w punkcie.

DEFINICJA

Definicja 3: Definicja Heinego granicy właściwej funkcji w punkcie

Mówimy, że funkcja ma granicę w punkcie , gdzie pewne sąsiedztwo jest zawarte w dziedzinie funkcji, jeżeli dla każdego nie stałego ciągu argumentów funkcji różnych od zbieżnego do granicy , ciąg wartości funkcji odpowiadających argumentom jest zbieżny do granicy .

UWAGA

Uwaga 2:

Definicję Heinego granicy właściwej funkcji w punkcie można zapisać symbolicznie symbolicznie: funkcja ma w punkcie granicę równą wtedy i tylko wtedy, gdy

. x0 x f(x) x x x3 x42 1 x x x x 1 2 3 4 f( ) f( ) f( ) f( ) g

Rysunek 2: Interpretacja geometryczna definicji Heinego granicy funkcji w punkcie

(4)

Rys. 2 przedstawia wykres funkcji z zaznaczonym na osi odciętych punktem , w którym funkcja nie ma wartości, ale w sąsiedztwie którego jest określona. Na osi rzędnych zaznaczono liczbę . Chcemy pokazać, że liczba jest granicą funkcji w punkcie . W tym celu wybieramy kolejne wyrazy ciągu argumentów funkcji różne od , który ma granicę i zaznaczamy na osi rzędnych wartości funkcji dla tych argumentów. Sprawdzamy, czy ciąg wartości funkcji lokalizuje się wokół liczby . Jeżeli tak jest, to spełniony jest warunek definicji Heinego.

UWAGA

Uwaga 3:

Zauważamy, ze definicja Cauchy’ego sformułowana jest w języku otoczeń i jest niewygodna jako narzędzie do wyliczania granicy. Definicja Heinego używa w swojej wypowiedzi pojęcia ciągu, dlatego też okazuje się, że znajomość metod liczenia granic ciągów można wykorzystać przy liczeniu granic funkcji właśnie poprzez bezpośrednie zastosowanie definicji Heinego.

TWIERDZENIE

Twierdzenie 1: o równoważności definicji Cauchy’ego i Heinego

(5)

PRZYKŁAD

Przykład 1:

Pokaż z definicji, że Rozwiązanie: Sposób I:

Skorzystajmy z definicji Cauchy'ego.

Bierzemy zatem dowolne . Mamy pokazać, że znajdziemy takie , że dla wszystkich argumentów i funkcji spełniających zależność zachodzi nierówność

Rozwiązujemy powyższą nierówność wyliczając zależność dla

, dla z drugiej strony dla mamy

co jest równoważne nierówności , czyli możemy przyjąć .

Stąd , dla oraz , dla , czyli dla każdej liczby da się dobrać liczbę taką, że spełniona jest nierówność dla wszystkich takich, że .

Sposób II:

Skorzystajmy z definicji Heinego.

Bierzemy zatem dowolny ciąg taki, że . Mamy pokazać, że Obliczamy granicę To dowodzi, że .

PRZYKŁAD

Przykład 2:

Oblicz z definicji . Rozwiązanie:

Do obliczenia granicy skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg zmierzający do i obliczamy .

Wyliczamy granicę .

Zatem .

(6)

DEFINICJA

Definicja 4: Granica właściwa funkcji w nieskończoności

Mówimy, że funkcja ma granicę w , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest zbieżny do granicy . Mówimy, że funkcja ma granicę w , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest zbieżny do granicy .

UWAGA

Uwaga 4:

Powyższe definicje możemy zapisać symbolicznie wtedy i tylko wtedy, gdy

6

4

2

20 40 60 80

0

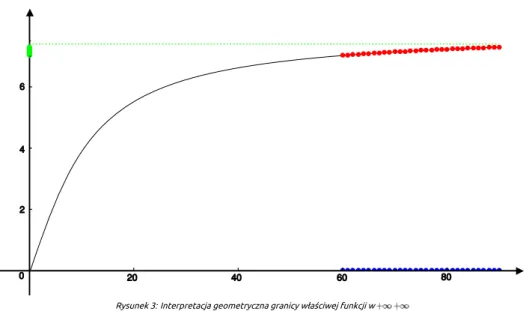
Rysunek 3: Interpretacja geometryczna granicy właściwej funkcji w

Rys. 3 przedstawia wykres funkcji określonej w przedziale oraz metodę wyznaczania granicy funkcji w nieskończoności

korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg rozbieżny do (niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg zbieżny, to funkcja ma granicę w nieskończoności, co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy znajdziemy prostą o równaniu , do której wykres funkcji zbliża się nieograniczenie wraz ze wzrostem wartości argumentów.

R

(7)

PRZYKŁAD

Przykład 3:

Oblicz z definicji . Rozwiązanie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów rozbieżny do . Obliczamy granicę ciagu wartości funkcji dla tych argumentów

. Czyli .

PRZYKŁAD

Przykład 4:

Oblicz . Rozwiązanie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg rozbieżny do . Obliczamy granicę wartości funkcji dla tych argumentów

Czyli .

UWAGA

Uwaga 5:

Granica funkcji w nieskończoności jest uogólnieniem pojęcia granicy ciągu, dlatego też wiele własności wyprowadzonych dla granic ciągów stosuje się do granicy funkcji w nieskończoności.

(8)

WNIOSEK

Wniosek 1:

, dla

DEFINICJA

Definicja 5: Granica niewłaściwa funkcji w punkcie

Mówimy, że funkcja ma granicę niewłaściwą w punkcie , jeżeli dla każdego nie stałego ciągu argumentów funkcji różnych od zbieżnego do granicy , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest rozbieżny do .

UWAGA

Uwaga 6:

Powyższe definicje możemy zapisać symbolicznie wtedy i tylko wtedy, gdy

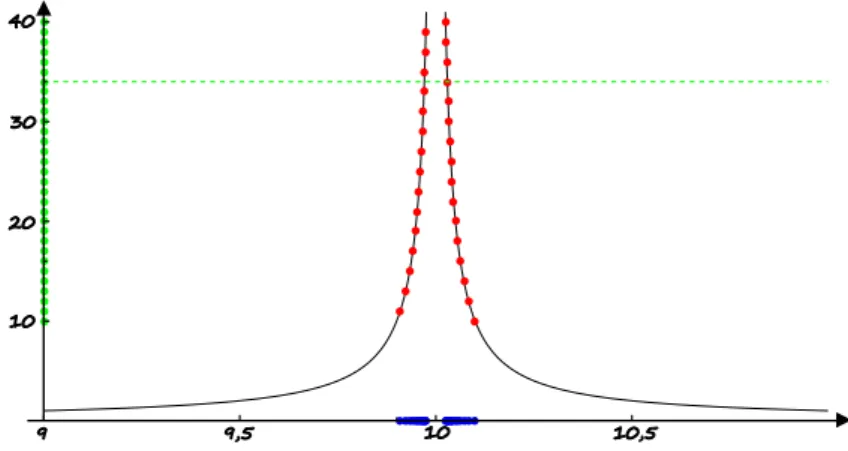
Rysunek 4: Interpretacja geometryczna granicy niewłaściwej funkcji w punkcie

R

(9)

Rys. 4 przedstawia wykres funkcji określonej w sąsiedztwie liczby oraz metodę wyznaczania granicy niewłaściwej funkcji w punkcie korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg zbieżny do (niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg rozbieżny do , to funkcja ma granicę niewłaściwą w punkcie , co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy dla dowolnej prostej o równaniu znajdziemy sąsiedztwo punktu takie, że dla argumentów z tego sąsiedztwa wykres funkcji leży powyżej prostej.

PRZYKŁAD

Przykład 5:

Oblicz granicę .

Rozwiązanie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów różnych od i zbieżny do . Obliczamy granicę ciagu wartości funkcji dla tych argumentów

.

Czyli .

DEFINICJA

Definicja 6: Granica niewłaściwa funkcji w nieskończoności

Mówimy, że funkcja ma granicę w , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do , ciąg wartości funkcji obliczonych dla wyrazów ciągu jest rozbieżny do .

UWAGA

Uwaga 7:

Powyższe definicje możemy zapisać symbolicznie

wtedy i tylko wtedy, gdy .

(10)

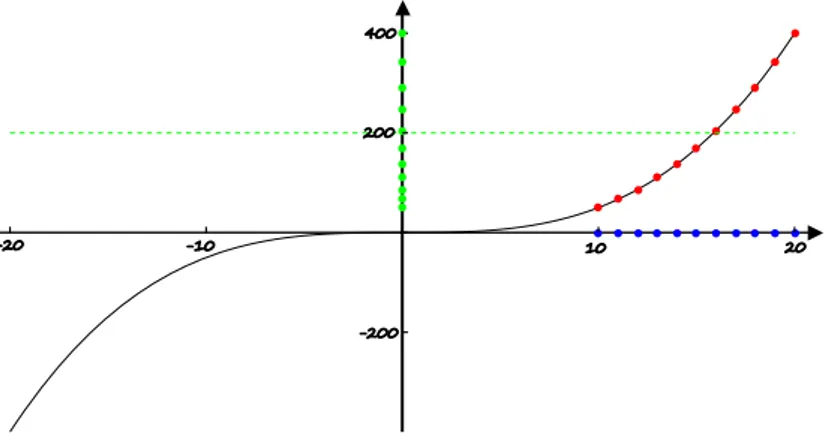
Rysunek 5: Interpretacja geometryczna granicy niewłaściwej funkcji w

Rys. 5 przedstawia wykres funkcji określonej w całym zbiorze liczb rzeczywistych oraz metodę wyznaczania granicy niewłaściwej

funkcji w nieskończoności, korzystając z definicji Heinego. Na osi odciętych wybieramy ciąg rozbieżny do (niebieski), wyznaczamy odpowiadające im punkty na wykresie funkcji (czerwone), a następnie rzutujemy je prostopadle na oś rzędnych otrzymując wartości funkcji dla argumentów będących wyrazami wyjściowego ciągu (zielone). Badamy zachowanie się ciągu wartości i jeżeli jest to ciąg rozbieżny do , to funkcja ma granicę niewłaściwą w nieskończoności , co zachodzi w przypadku badanej funkcji. Zauważmy również, że można tu stosować definicję Cauchy’ego i sprawdzać, czy dla dowolnej prostej o równaniu znajdziemy na osi odciętych przedział taki, że dla argumentów z tego przedziału wykres funkcji leży powyżej prostej.

PRZYKŁAD

Przykład 6:

Oblicz granicę . Rozwiąznie:

Skorzystamy z definicji Heinego. Bierzemy zatem dowolny ciąg argumentów rozbieżny do . Obliczamy granicę ciągu wartości funkcji dla tych argumentów

.

Czyli .

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 05:09:30

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=96f343d06b4055c59dec3c0c641800c3