Ciąg ograniczony

Ciąg ograniczony

Autorzy:

Katarzyna Czyżewska

Ciąg ograniczony

Ciąg ograniczony

Autor: Katarzyna Czyżewska

Zbadajmy zachowanie się ciągów ze względu na własność ograniczoności.

5 10 15 20 25 30 0.5 1.0 1.5 2.0 5 5 5 5 0 0 0 0 0

Rysunek 1: Ciąg ograniczony od góry

Rys. 1 przedstawia wykres ciągu, którego wszystkie wyrazy są mniejsze od liczby A=2.

5 10 15 20 25 30 2.0 2.5 0 5 0 5 0 5 0

Rysunek 2: Ciąg ograniczony od dołu

Rys. 2 przedstawia wykres ciągu, którego wszystkie wyrazy są większe od liczby A=-1,6.

Na Rys. 1 i Rys. 2 widzimy wykresy dwóch ciągów, przy czym wszystkie wyrazy pierwszego ciągu są mniejsze od pewnej liczby rzeczywistej i taki ciąg nazywamy ciągiem ograniczonym od góry, podczas gdy wszystkie wyrazy drugiego ciągu są większe od pewnej liczby rzeczywistej i nazywamy go ciągiem ograniczonym od dołu.

3

1

-1

-3

5 15 25

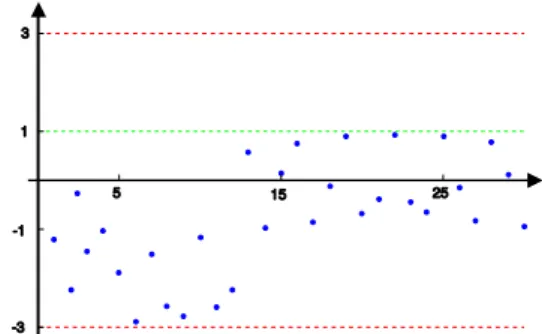
Rysunek 3: Wykres ciągu, którego wszystkie wyrazy są mniejsze od liczby 1, ale większe od liczby -3

Rys. 3 przedstawia wykres ciągu, którego wszystkie wyrazy są mniejsze od liczby 1, ale większe od liczby -3. Oznacza to, że wszystkie wyrazy tego ciągu leżą w przedziale .

Istnieją również ciągi, które są ograniczone zarówno od góry, jak i od dołu i taki ciąg nazywamy ograniczonym. Zauważamy, że wszystkie wyrazy ciągu ograniczonego leżą w przedziale , dla pewnej liczby .

[−3, 3]

5 10 15 20 25 30 - 60 - 40 - 20 20 40 0 0 0 0 0 0 5 0 5 0

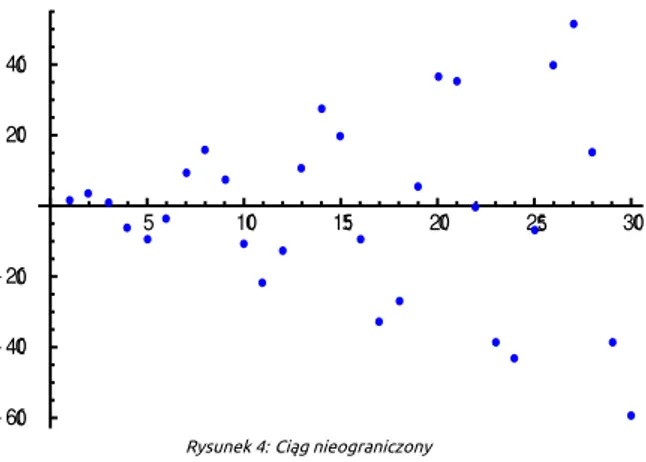
Rysunek 4: Ciąg nieograniczony

Rys. 4 przedstawia wykres ciągu, dla którego znajdą się wyrazy zarówno większe jak i mniejsze od dowolnej liczby rzeczywistej. Ciąg taki nie spełnia więc żadnego z warunków ograniczoności.

W przypadku, gdy nie znajdziemy takiej liczby, od której wszystkie wyrazy ciągu byłyby mniejsze, lub takiej, od której wszystkie wyrazy byłyby większe, to ciąg o tej własności nazywamy nieograniczonym.

DEFINICJA

Definicja 1: Ciąg ograniczony od góry

Definicja 1: Ciąg ograniczony od góry

Mówimy, że ciąg jest ograniczony od góry, jeżeli istnieje liczba taka, że dla każdego zachodzi .

DEFINICJA

Definicja 2: Ciąg ograniczony od dołu

Definicja 2: Ciąg ograniczony od dołu

Mówimy, że ciąg jest ograniczony od dołu, jeżeli istnieje liczba taka, że dla każdego zachodzi .

DEFINICJA

Definicja 3: Ciąg ograniczony

Definicja 3: Ciąg ograniczony

Mówimy, że ciąg jest ograniczony, jeżeli ciąg jest ograniczony od dołu i od góry, co jest równoważne warunkowi, że istnieje liczba taka, że dla każdego zachodzi .

Aby analitycznie zbadać, czy ciąg jest ograniczony od góry (albo od dołu) należy znaleźć liczbę rzeczywistą, dla której

spodziewamy się, że każdy wyraz ciągu będzie od niej mniejszy (albo większy), a następnie udowodnić, że rzeczywiście tak jest. Znaleźć taką liczbę można korzystając z wykresu ciągu lub z ogólnych zasad pozwalających ograniczać wartości wyrażeń. Warto zauważyć prosty fakt, że ciąg rosnący jest zawsze ograniczony od dołu, a ciąg malejący jest ograniczony od góry przez swój pierwszy wyraz.

( )

a

A ∈ R

n ∈ N

a

≤ A

( )

a

A ∈ R

n ∈ N

a

≥ A

( )

a

( )

a

PRZYKŁAD

Przykład 1:

Przykład 1:

Zbadaj ograniczoność ciągu . Rozwiązanie

Rozwiązanie

Zauważamy, że ciąg jest malejący, bo

Zatem dla każdego , .

Z drugiej strony dla wszystkich , czyli ciąg jest ograniczony.

PRZYKŁAD

Przykład 2:

Przykład 2:

Zbadaj ograniczoność ciągu . Rozwiązanie

Rozwiązanie

Zauważamy, że ciąg inaczej zachowuje się dla parzystych, a inaczej dla nieparzystych. Dla parzystych .

Pokażemy, że dla dowolnego od pewnego miejsca .

Rzeczywiście, nierówność jest spełniona dla każdego , a dla mamy

czyli zawsze znajdziemy tak duże , dla którego , a zatem ciąg nie jest ograniczony od góry. Analogicznie pokazujemy, że dla n nieparzystych, dla dowolnego , od pewnego miejsca .

Wykazaliśmy, że ciąg nie jest ograniczony od góry, ani od dołu.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 04:54:26

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=50844cf4a91ceafe94dae97e4429effc

Autor: Katarzyna Czyżewska

=

a

a

−

=

−

=

< 0

a

a

n ∈ N

a

<

a

=

> 0

a

n

( )

a

=

b

n

n

n

b

=

A

b

> A

A < 0

A ≥ 0

> A ⇔

− A − A > 0

− At − A > 0 ⇒

>

⇔ n >

4

2

⟺

t

₂

log

n ∈ N

b

> A

( )

b

A

b

< A

( )

b