Całkowanie przez podstawianie całek oznaczonych

(1)

Całkowanie przez

podstawianie całek

oznaczonych

Autorzy:

Witold Majdak

2019

(2)

TWIERDZENIE

Twierdzenie 1:

Twierdzenie 1: o całkowaniu przez podstawianie całek oznaczonych

o całkowaniu przez podstawianie całek oznaczonych

Jeżeli jest funkcją ciągłą, natomiast jest funkcją klasy taką, że oraz

, to zachodzi równość

DOWÓD DOWÓD

Skoro funkcja jest ciągła, to posiada funkcję pierwotną , a zatem . W konsekwencji

tak więc

Zauważmy, że w powyższych obliczeniach dwukrotnie użyliśmy twierdzenie Newtona-Leibniza, za pierwszym razem stosując je do funkcji podcałkowej oraz jej funkcji pierwotnej , a dalej do funkcji podcałkowej oraz jej funkcji pierwotnej .

Ponadto przedostatnia równość została uzyskana dzięki założeniu, że i .

CND. CND.

Zastosujmy twierdzenie o całkowaniu przez podstawienie do obliczenia przykładowych całek oznaczonych.

PRZYKŁAD

Przykład 1:

Zauważmy, że dokonaliśmy tu następującej zmiany wartości granic całkowania:

Tabela 1: Zmiana wartości granic całkowania, gdy

f : [a, b] → R

φ : [α, β] → [a, b]

C

1

_{φ(α) = a}

φ(β) = b

f(x)dx = f(φ(t)) (t)dt.

∫

a b

∫

α β

φ

′

f

g

f = g

′

f(φ(t)) (t) = (φ(t)) (t) = (g ∘ φ (t),

φ

′

_g

′

_φ

′

₎

′

f(φ(t)) (t)dt = (g ∘ φ (t)dt = g(φ(β)) − g(φ(α)) = g(b) − g(a) =

f(x)dx.

∫

α β

φ

′

_∫

α β

)

′

_∫

b a

(g ∘ φ)

′

_{g ∘ φ}

_f

_g

φ(α) = a φ(β) = b

dx =

=

− 1.

∫

0 1 x +1 x2 √

∣

t =

x

2

+ 1

dt = 2xdx

dt = xdx

1 2

∣

12

∫

1 2 dt t √

√ ∣∣

t

2 1

√

2

(t =x2+ 1)

x

0 1

t =

x

2

+ 1

_{1 2}

(3)

PRZYKŁAD

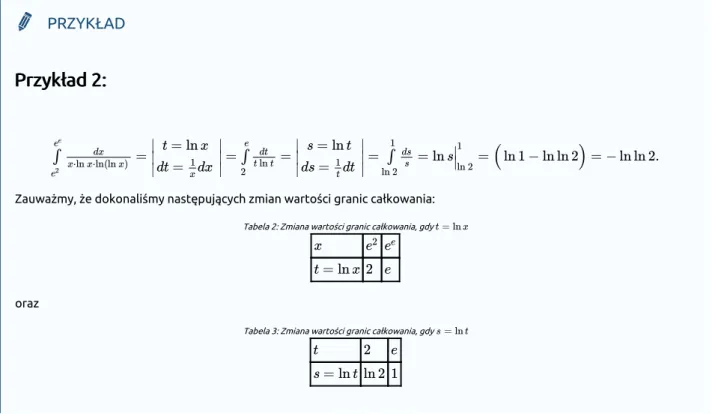
Przykład 2:

Zauważmy, że dokonaliśmy następujących zmian wartości granic całkowania:

oraz

Na podstawie twierdzenia o całkowaniu przez podstawienie możemy sformułować natępujące wnioski.

WNIOSEK

Wniosek 1: o całce z funkcji parzystej w przedziale symetrycznym względem zera

Jeżeli jest liczbą dodatnią, natomiast jest parzystą funkcją ciągłą, to

DOWÓD DOWÓD

Dokonując w pierwszej z całek występujących w powyższej sumie podstawienia i stosownej zmiany granic całkowania

otrzymujemy

Ostatnia równość wynika z faktu, że jest funkcją parzystą oraz zamiany symbolu zmiennej całkowania z na . CND. CND.

=

= ln s

= ( ln 1 − ln ln 2) = − ln ln 2.

∫

e2 ee dx x⋅ln x⋅ln(ln x)

∣

_{dt = dx}

t = ln x

₁ x

∣

∣ ∫

2 e dt t ln t

∣

_{ds = dt}

s = ln t

₁ t

∣

∫

ln 2 1 ds s

∣∣

1 ln 2 t = ln x

x

e

2

_e

e

t = ln x 2 e

s = ln t

t

2 e

s = ln t ln 2 1

a

f : [−a, a] → R

f(x)dx = 2 f(x)dx.

∫

−a a

∫

0 a

f(x)dx = f(x)dx + f(x)dx.

∫

−a a

∫

−a 0

∫

0 a

t = −x

t = −x

x

−a 0

t = −x a 0

− f(−t)dt + f(x)dx = f(−t)dt + f(x)dx = 2 f(x)dx.

∫

a 0

∫

0 a

∫

0 a

∫

0 a

∫

0 a

f

t x

(4)

WNIOSEK

Wniosek 2: o całce z funkcji nieparzystej w przedziale symetrycznym względem

zera

Jeżeli jest liczbą dodatnią, natomiast jest nieparzystą funkcją ciągłą, to

Rysunek 2:

Powyższe wnioski mają dość duże znaczenie w praktycznych obliczeniach, gdyż niejednokrotnie prościej jest znaleźć wartość funkcji pierwotnej w zerze niż w . W szczególności powyższy wniosek pozwala natychmiast podać wartość liczbową niektórych całek bez konieczności przeprowadzania złożonych rachunków.

a

f : [−a, a] → R

f(x)dx = 0.

∫

−a a I = f(x)dx∫ 0 a

−a

(5)

PRZYKŁAD

Przykład 3:

Możemy stwierdzić, że

ponieważ całkujemy po przedziale, który jest symetryczny względem zera, a funkcja sinus jest w nim nieparzysta.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-16 01:26:59

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=bd211455e2b3c92e6e174762285e8f44

Autor: Witold Majdak

xdx = 0,

∫

−π 2 π 2

sin

7