Skalarne równanie quasiliniowe dla funkcji n zmiennych niezależnych

(1)

Skalarne równanie

quasiliniowe dla funkcji n

zmiennych niezależnych

Autorzy:

Vsevolod Vladimirov

(2)

(1)

(2)

Skalarne równanie quasiliniowe dla funkcji n zmiennych niezależnych

Autor: Vsevolod Vladimirov

Schemat rozwiązywania równania quasiliniowego można uogólnić na przypadek funkcji zależnej od zmiennych ( ). Rozpoczniemy od rozwiązywania równania liniowego jednorodnego

Załóżmy że są funkcjami ciągłymi, które nie zerują się jednocześnie w żadnym punkcie pewnego zbioru Schemat rozwiązania równania jest następujący: zapisujemy układ równań

i znajdujemy niezależnych całek pierwszych

tego układu.

Funkcje nazywane są charakterystykamicharakterystykami. Żeby przekonać się, że charakterystyki są niezależne, wystarczy sprawdzić, czy rząd macierzy Jacobiego

w każdym punkcie jest maksymalny, czyli równy . Wykażemy

LEMAT

Lemat 1:

Funkcje charakterystyczne spełniają równanie ( 1 ). Dowód

Dowód Różniczkując równanie otrzymujemy

Ponieważ różniczka nie jest równa zeru, więc

WNIOSEK

Wniosek 1:

Dowolna gładka funkcja zachowuje stałą wartość na krzywych całkowych układu ( 2 ).

Dowód

Dowód Każda charakterystyka zachowuje stałą wartość na każdym rozwiązaniu układu ( 2 ), więc każda funkcja gładka, zależna

n

n > 2

( , , . . . . )

+ ( , , . . . . )

+. . . + ( , , . . . . )

= 0.

P

1

x

1

x

2

x

n _{∂ x}∂ z₁

P

2

x

1

x

2

x

n _{∂ x}∂ z₂

P

n

x

1

x

2

x

n _{∂ x}∂ z_n

, i = 1...n,

P

i

U ⊂

R

n

.

=

. . . .

= dt

d x1 P1 d x2 P2 d xn Pn

n − 1

( , , . . . . ) = ,

( , , . . . . ) = . . . . ,

( , , . . . . ) =

,

ψ

1

_x

₁

_x

₂

_x

_n

_C

₁

_ψ

2

_x

₁

_x

₂

_x

_n

_C

₂

_ψ

n−1

_x

₁

_x

₂

_x

_n

_C

_n−1

, . . . .

ψ

1

_ψ

n−1

J =

∂ ( , ,..._{∂ ( , ,... )}ψ_x1ψ2 ψn−1) 1x2 xn

( , , . . . ) ∈ U

x

1

x

2

x

n

n − 1

( , . . . ), k = 1, . . . n − 1

ψ

k

_x

₁

_x

n

( , , . . . . ) = ,

ψ

k

_x

₁

_x

₂

_x

n

C

k

0 = d

ψ

k

=

_∑

n

d = (

) dt.

i=1 ∂ ψ k ∂ xi

x

i

∑

n i=1 ∂ ψ k ∂ xi

P

i

dt

= 0.

∑

n i=1

P

i∂ ψ k ∂ xi

Φ( , , . . .

ψ

1

_ψ

2

_ψ

n−1

)

(3)

(3) wyłącznie od charakterystyk danego układu, również zachowuje stałą wartość na jego rozwiązaniach.

WNIOSEK

Wniosek 2:

Dowolna różniczkowalna funkcja

spełnia równanie ( 1 ).

Dowód

Dowód Skorzystajmy ze wzoru na pochodną cząstkową złożonej funkcji

Zatem

Zmieniając kolejność sumowania, otrzymamy

Ostatnia równość wynika stąd, że, na mocy lematu 1, suma w nawiasach klamrowych jest równa zeru. Zachodzi również

TWIERDZENIE

Twierdzenie 1:

Dowolne rozwiązanie równania ( 1 ) można przedstawić w postaci ( 3 ). Dowód tego twierdzenia pomijamy.

PRZYKŁAD

Przykład 1:

Rozwiążmy równanie Rozwiązanie Rozwiązanie

1. Zapisujemy układ charakterystyczny:

z = Φ( ,

ψ

1

_ψ

2

, . . .

_ψ

n−1

)

=

⋅

.

∂ z ∂ xi

∑

n−1 k=1 _{∂ ψ}∂ Φk ∂ ψk ∂ xi

⋅

=

⋅

.

∑

n i=1

P

i _{∂ x}∂ z_i

∑

ni=1

P

i

∑

n−1k=1 _{∂ ψ}∂ Φk ∂ ψ k ∂ xi

⋅

=

{

⋅

} = 0.

∑

n i=1

P

i _{∂ x}∂ z_i

∑

k=1n−1 _{∂ ψ}∂ Φk

∑

ni=1

P

i ∂ ψk ∂ xi

+

+. . . +

= 0.

x

1

x

n _{∂ x}∂ z₁

x

2

x

n _{∂ x}∂ z₂

x

n−1

x

n_{∂ x}∂ z_n−1

=

=. . . =

=

= dt.

d x1 x1xn d x2 x2xn d xn−1 xn−1xn d xn 0

(4)

(5)

(6) Całkując ostatnie równanie układu, otrzymujemy charakterystykę

Przyrównując teraz po kolei pierwsze wyrażenie do drugiego, trzeciego i t.d., otrzymamy całkując pozostałe charakterystyki:

2. Obliczamy macierz Jacobiego

Skreślając pierwszą kolumnę macierzy , otrzymamy macierz kwadratową wymiaru

Rozwijając wyznacznik tej oraz kolejnych macierzy względem pierwszej kolumny, otrzymamy:

Wyrażenie to nie jest równe zeru i jest dobrze okreslone w dowolnym obszarze, który nie przecina żadnej z osi współrzędnych. 3. Przedstawiamy rozwiązanie ogólne równania w postaci

Okazuje się, że rozwiązywanie quasiliniowego niejednorodnego równania skalarnego zawsze można sprowadzić do rozwiązywanie równania liniowego jednorodnego, w którym poszukiwana funkcja ma o jedną zmienną więcej. Rozpatrzmy równanie postaci u

Analogicznie, jak dla przypadku funkcji zależnej od dwóch zmiennych, można poszukiwać rózwiązania równania ( 4 ) w postaci uwikłanej

dodając warunek który umożliwia przejście do jawnej postaci. Traktując w powyższym wzorze jako funkcję zmiennych i różniczkując względem lewą i prawą stronę wzoru

otrzymamy: Zatem

:

= .

ψ

1

_x

n

C

1

:

= ,

:

= , . . .

:

=

.

ψ

2 x1 x2

C

2

ψ

3 x1 x3

C

3

ψ

n−1 x1 xn−1

C

n−1

J =

⎛

⎝

⎜

0,

1/ ,

x

2

1/ ,

x

3

. . .

1/

x

n−1

,

0,

− / ,

x

1

x

22

0,

. . .

0,

− / ,

x

1

x

23

. . .

0,

. . . .

. . .

0,

. . .

0,

. . .

− /

x

1

x

2n−1

,

1

0

0 . . .

0 ⎞

⎠

⎟

J

(n − 1) × (n − 1)

=

.

J

1

⎛

⎝

⎜

0,

− / ,

x

1

x

22

0,

. . .

0,

− / ,

x

1

x

23

. . .

. . . .

0....

. . . .

0,

. . . .

− /

x

1

x

2n−1

,

1

0

0 . . . .

0 ⎞

⎠

⎟

det =

J

1 x_x12

. . . .

=

.

2 x1 x2 3 x1 x2 n−1 xn−2 1 (x2x3...xn−1)2

z = Φ( , , , . . . .

x

n x_x1₂ x_x1₃ _xx_n−11

) .

( , , . . . . ; z)

= R ( , , . . . . ; z) .

∑

n i=1

P

i

x

1

x

2

x

n _{∂ x}∂ z_i

x

1

x

2

x

n

u( , , . . . . ; z) = 0,

x

1

x

2

x

n

( , , . . . . ; z) ≠ 0,

u

z

x

1

x

2

x

n

z

, , . . . .

x

1

x

2

x

n

x

i

u[ , , . . . . ; z( , , . . . , )] = 0,

x

1

x

2

x

n

x

1

x

2

z

n

+

= 0,

i = 1, 2, . . . . , n.

∂ u ∂ xi ∂ u ∂ z ∂ x∂ zi

= −

.

∂ z ∂ xi ∂ u/∂ xi ∂ u/∂ z

(5)

(7)

(8)

(9) Podstawiając ( 6 ) do równania ( 1 ), mnożąc przez i przenosząc wszystkie wyrazy na lewą stronę, otrzymamy liniowe jednorodne równanie względem funkcji :

Żeby zatem określić rozwiązanie równania ( 4 ), należy rozwiązać równanie ( 7 ) wzlędem funkcji , a następnie, o ile jest to możliwe, uzyskać jawną postać , rozwikłując wzór względem ostatniej zmiennej. Procedura rozwiązania równania ( 7 ) jest nam już znana z poprzednimch rozważań: zapisujemy stowarzyszone równanie charakterystyczne

znajdujemy niezależnych całek pierwszych

a następnie konstruujemy z nich rozwiązanie ogólne postaci

gdzie jest to dowolna funkcja zmiennych, różniczkowalna w sposób ciągły po każdym ze swoich argumentów.

UWAGA

Uwaga 1:

Oprócz rozwiązania ogólnego ( 8 ) , równanie ( 7 ), a zatem również i ( 4 ) może posiadać rozwiązania specjalne

dla których

Wówczas jednak lewa strona powyższego wzoru zeruje się przy uwzględnieniu warunku ( 9 ) . W pewnym sensie rozwiązań takich nie jest dużo, i dlatego indeksujemy je, na ogół skończonym, podzbiorem Co więcej, rozwiązań takich może nie istniec wcale.

Pokażemy że pole wektorowe skojarzone z rozpatrzonym wcześniej układem, w którym, na skutek bifurkacji Hopfa (zob. moduł ), powstaje nieliniowe rozwiązanie okresowe, posiada co najmniej jedno rozwiązanie osobliwe.

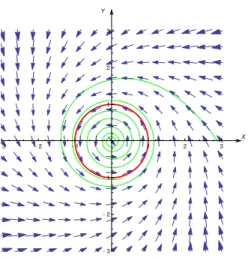
- 3 - 2 - 1 1 2 3 X - 3 - 2 - 1 1 2 3 Y

Rysunek 1: Wizualizacja pola wektorowego określonego przez prawe strony układu ( 10 )-( 11 ). oraz trzy różne rozwiązania tego układu. Jedynie rozwiązanie (czerwony okrąg) ma prostą geometryczną strukturę, jako że nie zależy od zmiennej kątowej .

−u

z

u

( , , . . . . ; z)

+ R ( , , . . . . ; z)

= 0.

∑

n i=1

P

i

x

1

x

2

x

n _{∂ x}∂ u_i

x

1

x

2

x

n ∂ u_{∂ z}

u

z = φ( , . . . )

x

1

x

n

u( , , . . . . ; z) = 0

x

1

x

2

x

n

=

=. . . =

=

,

d x1 P1 d x2 P2 d xn Pn d z R

n

( , . . ; z) = , . . . . , ( , . . ; z) =

,

ψ

1

_x

₁

_x

_n

_C

₁

_ψ

n

_x

1

x

n

C

n

Φ( , . . . . ) = 0,

ψ

1

_ψ

n

Φ

n

( , , . . . . ; z) = 0,

k ∈ I,

Φ

k

x

1

x

2

x

n

( , , . . . . ; z)

+ R ( , , . . . . ; z)

≠ 0,

∑

n i=1

P

i

x

1

x

2

x

n ∂ Φ_{∂ x}k_i

x

1

x

2

x

n ∂ Φ_{∂ z}k

I ∈ N.

+ = μ x2 _y2 ϕ

(6)

(10) (11) (12) (13) (14) (15) (16) (17) (18) (19) Rozpatrzmy znany z układ dynamiczny

dopełniony równaniem

Układ jest postacią charakterystyczną równania

Ponieważ analiza problemu w układzie katrezjańskim jest bardzo trudna, skorzystajmy, jak wyżej przy rozpatrzeniu bifurkacji Hopfa, z reprezentacji biegunowej. Najprościej można do niej przejść, wprowadzając zmienną zespolonąc i zapisując postać zespoloną układu ( 10 ), ( 11 ) :

(równanie ( 12 ) przy tym, oczywiście, nie ulegnie zmianie). Przechodząc dalej do reprezentacji biegunowej , otrzymamy równanie:

Przyrównując do siebie części rzeczywiste i zespolone występujące w równaniu, oraz dodając ( 12 ), otrzymamy następujący układ charakterystyczny:

Układowi temu odpowiada biegunowa reprezentacja równania ( 13 ):

Przyrównując do siebie i całkując najpierw pierwszy i drugi, a następnie, na przykład, drugi i trzeci wyraz układu charakterystyk

otrzymamy następujące całki pierwsze:

Zatem równanie

gdzie jest to dowolna różniczkowalna funkcja dwóch zmiennych, określa w postaci niejawnej rozwiązanie ogólne równania ( 18 ).

Rozpatrzmy teraz funkcję

Działając na nią operatorem występującym w ( 18 ) otrzymamy, że

= μ x − ωy − x ( + ) ,

d x d t

x

2

y

2

= ωx + μ y − y ( + ) ,

d y d t

x

2

y

2

= 0.

d u d t

[μ x − ωy − x ( + )]

x

2

_y

2 ∂ u

+ [ωx + μ y − y ( + )]

= 0.

∂ x

x

2

y

2 ∂ u∂ y

z = x + i y

= (μ + i ω) z − z|z

d z d t

|

2

z = r e

i φ

+

r

= (μ + i ω) r

−

.

d r d t

e

i φ d φd t

e

i φ

e

i φ

r

3

e

i φ

= r (μ − ) ,

d r d t

r

2

= ω,

d φ d t

= 0.

d u d t

r (μ − )

r

2 ∂ u

+ ω

= 0.

∂ r ∂ φ∂ u

=

d r r (μ− )r2 d φ_ω d u₀

:

exp

φ =

,

: u = .

ϕ

1 r2−μ r2 2 μ_ω

C

1

ϕ

2

C

2

Φ[

r2_r−μ2

exp

2 μ_ω

φ, u] = 0,

Φ

: − μ = 0.

Φ

1

r

2

{r (μ − )

2

+ ω

}

₁

= 2 (μ − )

2 2

= 0.

=0 1

(7)

Równanie określa zatem rozwiązanie osobliwe nie należące do rodziny ( 19 ).

Interpretację geometryczną wyjaśniającą genezę rozwiązania osobliwego można pokazać na Rys. 1. Jest tam pokazane pole wektorowe, odpowiadające prawym stronom układu ( 10 ) - ( 11 ) oraz trajektoria fazowa, odpowiadająca rozwiązaniu okresowemu, które jest reprezentowane równaniem

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 07:35:11

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=0dd237944b7812e2b9898a51310f0bce