Pochodne wyższych rzędów. Wzór Taylora

(1)

Pochodne wyższych rzędów.

Wzór Taylora

Autorzy:

Tomasz Zabawa

(2)

Pochodne wyższych rzędów. Wzór Taylora

Autor: Tomasz Zabawa

Możemy obliczyć pochodną funkcji pochodnej. W ten sposób otrzymujemy pochodną rzędu drugiego zadanej funkcji, a także pochodne wyższych rzędów. Pojęcie pochodnych wyższych rzędów znajduje zastosowanie między innymi we wzorze Taylora, który umożliwia przybliżanie funkcji w lepszy sposób niż robi to różniczka funkcji czy geometrycznie styczna.

DEFINICJA

Definicja 1: Pochodna rzędu

Definicja 1: Pochodna rzędu funkcji w punkcie

funkcji w punkcie

Niech .

Pochodną (właściwą) rzędu

Pochodną (właściwą) rzędu funkcji funkcji w punkcie w punkcie (lub pochodną pochodną -tego rzędu funkcji -tego rzędu funkcji w punkcie w punkcie ) oznaczamy przez i definiujemy jako

o ile funkcja jest określona w otoczeniu punktu i istnieje pochodna funkcji w punkcie . Przyjmujemy, że .

DEFINICJA

Definicja 2: Funkcja pochodna rzędu

Funkcję określoną w przedziale , której wartości w punktach są równe , nazywamy funkcją pochodną rzędu funkcją pochodną rzędu funkcji

funkcji w przedziale w przedziale lub pochodną pochodną -tego rzędu funkcji -tego rzędu funkcji w przedziale w przedziale , lub też -tą pochodną funkcji -tą pochodną funkcji w przedziale w przedziale i oznaczamy dla .

UWAGA

Uwaga 1:

Pochodne wyższych rzędów oznaczamy również w następujący sposób:

Ponadto przyjmuje się oznaczenie:

UWAGA

Uwaga 2:

Dla istnienia pochodnej rzędu funkcji w punkcie konieczne jest istnienie w pewnym otoczeniu punktu . Natomiast dla istnienia pochodnej rzędu funkcji w przedziale otwartym konieczne jest istnienie w tym samym przedziale otwartym , ponieważ dla każdego punktu z przedziału otwartego istnieje otoczenie tego punktu, które zawiera się w tym przedziale. Są to warunki konieczne istnienia pochodnej rzędu , ale nie są to warunki wystarczające, czyli jest możliwa sytuacja, gdy istnieje pochodna rzędu danej funkcji, ale pochodna rzędu już nie.

n

n ∈ N

n

f

x

0

n

f

x

0

( )

f

(n)

_x

₀

( ) =

( ) dla n ≥ 2,

f

(n)

_x

₀

_[

_f

(n−1) ′

_]

_x

₀

f

(n−1)

_x

₀

_f

(n−1)

_x

₀

( ) = ( )

f

(1)

_x

₀

_f

′

_x

₀

n

I

x ∈ I

f

(n)

(x)

_n

f

I

n

f

I

n

f

I

f

(n)

_{n ∈ N}

( ) = ( ),

f

(2)

_x

₀

_f

′′

_x

₀

( ) =

( ).

f

(3)

_x

₀

_f

′′′

_x

₀

( ) = f( ).

f

(0)

_x

₀

_x

₀

n

f

x

0

f

(n−1)

x

0

n

f

I

f

(n−1)

I

n

n − 1

n

(3)

UWAGA

Uwaga 3:

jest nazywana definicją indukcyjną, ponieważ pochodną rzędu definiujemy za pomocą pochodnej rzędu , czyli definiujemy pojęcie dla za pomocą tego samego pojęcia określonego dla liczb naturalnych mniejszych od .

Indukcyjnie również definiujemy pochodne jednostronne wyższego rzędu:

DEFINICJA

Definicja 3: Pochodna lewostronna rzędu

Definicja 3: Pochodna lewostronna rzędu funkcji w punkcie

funkcji w punkcie

Niech .

Pochodną lewostronną (właściwą) rzędu

Pochodną lewostronną (właściwą) rzędu funkcji funkcji w punkcie w punkcie oznaczamy przez i definiujemy jako

o ile funkcja jest określona w otoczeniu lewostronnym punktu i istnieje pochodna lewostronna funkcji w punkcie . Przyjmujemy, że .

DEFINICJA

Definicja 4: Pochodna prawostronna rzędu

Definicja 4: Pochodna prawostronna rzędu funkcji w punkcie

funkcji w punkcie

Niech .

Pochodną prawostronną (właściwą) rzędu

Pochodną prawostronną (właściwą) rzędu funkcji funkcji w punkcie w punkcie oznaczamy przez i definiujemy jako

o ile funkcja jest określona w otoczeniu prawostronnym punktu i istnieje pochodna prawostronna funkcji w punkcie . Przyjmujemy, że .

Pochodną wyższego rzędu w przedziale definiujemy analogicznie do pochodnej rzędu pierwszego w przedziale:

n

n − 1

n ∈ N

n

n ∈ N

n

f

x

0

f

−(n)

( )

x

0

( ) =

( ) dla n ≥ 2,

f

−(n)

x

0

[

f

(n−1) ′

]

₋

x

0

f

(n−1)

_x

₀

_f

(n−1)

x

0

f

−(1)

( ) = ( )

x

0

f

′−

x

0

n

n ∈ N

n

f

x

0

f

+(n)

( )

x

0

( ) =

( ) dla n ≥ 2,

f

₊(n)

x

0

[

f

(n−1) ′

]

₊

x

0

f

(n−1)

_x

₀

_f

(n−1)

x

0

f

+(1)

( ) = ( )

x

0

f

+′

x

0

(4)

DEFINICJA

Definicja 5: Pochodna rzędu

Definicja 5: Pochodna rzędu funkcji w przedziale

funkcji w przedziale

Mówimy, że funkcja funkcja ma pochodną rzędu ma pochodną rzędu w przedziale otwartym w przedziale otwartym , gdzie , gdy funkcja ma pochodną rzędu w każdym punkcie tego przedziału.

Mówimy, że funkcja funkcja ma pochodną rzędu ma pochodną rzędu w przedziale domkniętym w przedziale domkniętym , gdzie , gdy funkcja ma pochodną rzędu w przedziale otwartym i pochodną prawostronną rzędu w i pochodną lewostronną rzędu w

.

Mówimy, że funkcja funkcja ma pochodną rzędu ma pochodną rzędu w przedziale w przedziale , gdzie , gdy funkcja ma pochodną rzędu w przedziale otwartym i pochodną lewostronną rzędu w .

Mówimy, że funkcja funkcja ma pochodną rzędu ma pochodną rzędu w przedziale w przedziale , gdzie , gdy funkcja ma pochodną rzędu w przedziale otwartym i pochodną prawostronną rzędu w .

PRZYKŁAD

Przykład 1:

Obliczyć pochodną rzędu drugiego (czyli drugą pochodną) funkcji oraz pochodną rzędu trzeciego (czyli trzecią pochodną) funkcji .

Zauważmy, że gdybyśmy policzyli piątą pochodną funkcji otrzymamy też liczbę: . I tak dalej. Są to szczególne przypadki następującej obserwacji:

UWAGA

Uwaga 4:

Niech będzie wielomianem stopnia o współczynniku przy , czyli . Wtedy:

Wykorzystując pochodne wyższych rzędów możemy sformułować twierdzenie o wzorze Taylorawzorze Taylora.

n

f

n

(a, b)

−∞ ≤ a < b ≤ ∞

f

n

f

n

[a, b]

−∞ < a < b < ∞

f

n

(a, b)

n a

n

b

f

n

(a, b]

−∞ ≤ a < b < ∞

f

n

(a, b)

n b

f

n

[a, b)

−∞ < a < b ≤ ∞

f

n

(a, b)

n a

f(x) = e

x2

g(x) = x

3

(x) =

f

′′

(x) =

g

′′′

(

e

= ( 2x =

2x2x +

2 =

(4 + 2)

x2

)

′′

_e

x2

)

′

_e

x2

e

x2

e

x2

x

2

(

x

3

₎

′′′

= (3

_x

2

₎

′′

= (3 ⋅ 2x = 3 ⋅ 2 ⋅ 1 = 6

₎

′

x

5

_{5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5!}

W

n

n ∈ N

a

n

x

n

(x) =

+

+. . . + x +

W

n

a

n

x

n

a

n−1

x

n−1

a

1

a

0

(x) = n! ⋅ ,

W

n(n)

a

n

(x) = 0.

W

n(n+1)

(5)

TWIERDZENIE

Twierdzenie 1: o wzorze Taylora z resztą Lagrange'a

Jeżeli

1. funkcja ma ciągłą pochodną (właściwą) rzędu w przedziale , 2. funkcja ma pochodną (właściwą) rzędu w przedziale , to

istnieje takie, że

gdzie .

Twierdzenie jest prawdziwe również dla przedziału .

TWIERDZENIE

Twierdzenie 2: o wzorze Taylora z resztą Lagrange'a

Jeżeli

1. funkcja ma ciągłą pochodną (właściwą) rzędu w przedziale , 2. funkcja ma pochodną (właściwą) rzędu w przedziale , to

istnieje takie, że

gdzie .

UWAGA

Uwaga 5:

Wyrażenie

nosi nazwę wielomianu Taylora stopnia wielomianu Taylora stopnia w punkcie w punkcie , natomiast

jest nazywane -tą resztą Lagrange'a w punkcie -tą resztą Lagrange'a w punkcie .

f

n

[ , x]

x

0

f

n + 1

( , x)

x

0

c ∈ ( , x)

x

0

f(x) = f( ) +

x

0 f( )

(x − ) +

(x −

+. . . +

(x −

+

,

′_x 0 1!

x

0 f ( ) ′′_x 0 2!

x

0

)

2 f ( ) (n)_x 0 n!

x

0

)

n

R

n

=

(x −

R

n f (c) (n+1) (n+1)!

x

0

)

n+1

[x, ]

x

0

f

n

[x, ]

x

0

f

n + 1

(x, )

x

0

c ∈ (x, )

x

0

f(x) = f( ) +

x

0 f( )

(x − ) +

(x −

+. . . +

(x −

+

,

′_x 0 1!

x

0 f ( ) ′′_x 0 2!

x

0

)

2 f ( ) (n)_x 0 n!

x

0

)

n

R

n

=

(x −

R

n f (c) (n+1) (n+1)!

x

0

)

n+1

f( ) +

x

0 f( )

(x − ) +

(x −

+. . . +

(x −

′_x 0 1!

x

0 f ( ) ′′_x 0 2!

x

0

)

2 f ( ) (n)_x 0 n!

x

0

)

n

x

0

=

(x −

R

n f (c) (n+1) (n+1)!

x

0

)

n+1

n

x

0

(6)

UWAGA

Uwaga 6:

Wzór Taylora dla , czyli wzór postaci:

gdzie , a leży między liczbami i , nosi nazwę wzoru Maclaurinawzoru Maclaurina. Analogicznie do wzoru Taylora w ogólnej postaci wyrażenie

nosi nazwę wielomianu Maclaurina stopnia wielomianu Maclaurina stopnia , natomiast

jest nazywane -tą resztą Lagrange'a-tą resztą Lagrange'a.

PRZYKŁAD

Przykład 2:

Wyznaczmy wzór Taylora dla funkcji w z resztą oraz dla funkcji w z resztą i . Dla funkcji mamy:

i tak dalej, zatem dla : Stąd

gdzie , a leży między argumentami i . Natomiast dla funkcji mamy:

Zatem

gdzie , a leży między argumentami i . Natomiast

gdzie , a leży między argumentami i .

= 0

x

0

f(x) = f(0) +

f′_1!(0)

x +

f′′_2!(0)

x

2

+. . . +

f(n)(0)

+

,

n!

x

n

R

n

=

R

n f (c) (n+1) (n+1)!

x

n+1

c

0 x

f(0) +

f′_1!(0)

x +

f′′_2!(0)

x

2

+. . . +

f(n)(0) n!

x

n

=

R

n f (c) (n+1) (n+1)!

x

n+1

n

f(x) = 2

x

_x

_{= 1}

0

R

5

g(x) = sin x

x

0

= π

R

5

R

6

f

f(x) = ,

2

x

(x) = ln 2,

f

′

₂

x

(x) = (ln 2 ,

f

′′

2

x

₎

2

(x) = (ln 2 ,

f

′′′

₂

x

₎

3

f(1) = 2,

(1) = 2 ln 2,

f

′

(1) = 2(ln 2 ,

f

′′

)

2

(1) = 2(ln 2

f

′′′

₎

3

n ∈ N

(x) = (ln 2 ,

(1) = 2(ln 2 .

f

(n)

₂

x

₎

n

_f

(n)

₎

n

2

x

₌

=

2 +

2 ln 2

_1!

(x − 1) +

2(ln 2)

_2!

2

(x − 1 +

)

2

2(ln 2)

3

(x − 1 +

3!

)

3

+

2(ln 2)

_4!

4

(x − 1 +

)

4

2(ln 2)

5

(x − 1 + ,

5!

)

5

R

5

=

(x − 1

R

5 2c(ln 2) 6 6!

)

6

c

x 1

g

g(x) = sin x

(x) = cos x,

g

′

(x) = − sin x,

g

′′

(x) = − cos x,

g

′′′

(x) = sin x,

g

(4)

(x) = cos x,

g

(5)

(x) = − sin x,

g

(6)

(x) = − cos x.

g

(7)

g(π) = 0

(π) = −1,

g

′

(π) = 0,

g

′′

(π) = 1,

g

′′′

(π) = 0,

g

(4)

(π) = −1,

g

(5)

(π) = 0,

g

(6)

sin x = − (x − π) + (x − π − (x − π + ,

1 1! 3!1

)

3 5!1

)

5

R

5

=

(x − π

R

5 − sin c_6!

)

6

c

x π

sin x = − (x − π) + (x − π − (x − π + ,

1 1! 3!1

)

3 5!1

)

5

R

6

=

(x − π

R

6 − cos c^_7!

)

7

c^

x π

(7)

PRZYKŁAD

Przykład 3:

Wyznaczmy wzór Maclaurina dla funkcji z resztą oraz wielomian Maclaurina stopnia funkcji . W przypadku wzoru Maclaurina nie mamy podanego , bo z definicji .

Zauważmy, że dla dowolnego : Stąd

gdzie , a leży między argumentami i . Natomiast wielomian Maclaurina stopnia funkcji ma postać: czyli

UWAGA

Uwaga 7:

Wzór Taylora pozwala przybliżyć zadaną funkcję wielomianem. Gdy rozważamy wielomian Taylora stopnia pierwszego, to otrzymujemy przybliżenie funkcji analogiczne do przybliżenia przez różniczkę funkcji:

Im wyższy stopień wielomianu Taylora tym dokładniejsze jest przybliżenie funkcji. W szczególności zauważmy, że błąd przybliżenia funkcji przez wielomian Taylora stopnia spełnia warunek:

Na podstawie tego wzoru możemy powiedzieć, że błąd jaki popełniamy przybliżając funkcję przez wielomian Taylora stopnia dąży do zera szybciej niż . Powyższy wzór możemy również zapisać w postaci: .

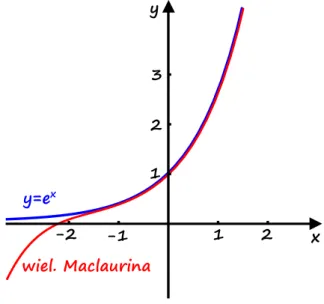
Ilustracją graficzną tej uwagi niech będą wykresy funkcji i ich przybliżeń przez wielomiany Taylora wyliczone w ostatnich przykładach.

Rysunek 1: Wykres funkcji oraz wykres jej wielomianu Taylora stopnia w .

Zwróćmy uwagę, że dla funkcji wielomianu Taylora stopnia 5 w i wielomianu Taylora stopnia 6 w ma identyczną postać, bo .

f(x) = e

x

_R

₅

_n

_f

x

0

x

0

= 0

n ∈ N

(x) =

i

(0) = 1.

f

(n)

_e

x

_f

(n)

= 1 + x +

+

+ ,

e

x 1 1! 2!1

x

2 3!1

x

3 4!1

x

4 5!1

x

5

R

5

=

R

5 e_6!c

x

6

c

x 0

n

f

1 + x +

1

+

+. . . +

1! 2!1

x

2 3!1

x

3 4!1

x

4 5!1

x

5 n!1

x

n

.

∑

n k=0 x k k!

f(x) ≈ f( ) + ( )(x − ).

x

0

f

′

x

0

x

0

n

= 0.

lim

x→x0 f(x)−(f( )+x0 f′ x0( )_1! (x− )+...+x0 f(n) x0_n!( )(x−x0)n) (x−x0)n

n

(x − x

0

)

n _x→x

lim

= 0

0 Rn (x−x0)n f(x) = 2x ₅ _x₀_{= 1}

g(x) = sin x

x

0

= π

x

0

= π

(π) = 0

g

(6)

(8)

Rysunek 2: Wykres funkcji oraz wykres jej wielomianu Taylora stopnia (lub ) w .

Rysunek 3: Wykres funkcji oraz wykres jej wielomianu Maclaurina stopnia .

Należy jednak zaznaczyć, że wykresy powyższych funkcji i ich wielomianów Taylora nie pokrywają się w żadnym przedziale. Dla funkcji różniczkowalnej wystarczająco wiele razy możemy, szacując resztę , ustalić stopnień wielomianu Taylora w punkcie

, tak aby przybliżenie danej funkcji przez ten wielomian Taylora miało zadaną z góry dokładność, czyli błąd przybliżenia był mniejszy lub równy od zadanej wartości. W szczególności przy pomocy wzoru Taylora możemy określić przybliżoną wartość funkcji dla zadanego argumentu z zadaną z góry dokładnością.

g(x) = sinx 5 6 x0= π

f(x) = ex ₅

R

n

(9)

PRZYKŁAD

Przykład 4:

Korzystając ze wzoru Maclaurina dla funkcji , obliczmy z dokładnością do 0,0001 wartość liczby . Wielomian Maclaurina stopnia funkcji ma postać:

a -ta reszta , gdzie . Zauważmy, że . Chcemy określić wartość z dokładnością do , czyli aby , zatem

Nie znamy wartości , wiemy jedynie, że , więc zastępujemy liczbą, dla której powyższe wyrażenie przyjmie wartość większą lub równą od wartości dla dowolnego . Jeżeli tak postąpimy, to nasze oszacowanie błędu będzie dobre niezależnie, jaka jest rzeczywista wartość . Wiemy, że liczba jest mniejsza od 3, zatem dla każdego

. W tej sytuacji chcemy, aby

Zauważmy, że , a , więc dobrą wartością będzie liczba naturalna taka, że . Wnioskujemy stąd, że wystarczy obliczyć wartość wielomianu Maclaurina stopnia 7 dla i otrzymamy szukaną przybliżoną wartość z dokładnością do 0,0001.

Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie

http://creativecommons.org/licenses/by-sa/3.0/pl/.

Data generacji dokumentu: 2019-04-15 06:15:30

Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=050b1a350863fcaef74d23a053e7160a