Granica ciągu
Autorzy:
Katarzyna Czyżewska
Granica ciągu
Granica ciągu
Autor: Katarzyna Czyżewska
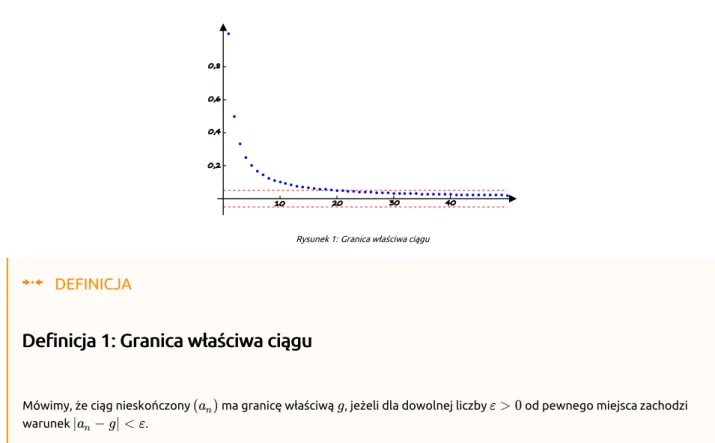
Dla kolejnych rozważań zakładamy, że ciąg jest nieskończony. Zastanówmy się, jak zachowują się wyrazy ciągu , jeżeli jest coraz większe, czyli mówimy, że zmierza do nieskończoności. Na Rys. 1 widzimy ciąg o wyrazach dodatnich, którego wyrazy, wraz ze wzrostem wartości , coraz bardziej zbliżają się do liczby zero, nigdy tej wartości nie osiągając. Jeżeli jednak wybierzemy liczbę , dowolnie bliską zeru, to nieskończenie wiele wyrazów ciągu leży w przedziale .
Rysunek 1: Granica właściwa ciągu
DEFINICJA
Definicja 1: Granica właściwa ciągu
Definicja 1: Granica właściwa ciągu
Mówimy, że ciąg nieskończony ma granicę właściwą , jeżeli dla dowolnej liczby od pewnego miejsca zachodzi
warunek .
Komentarz Komentarz
W wielu sytuacjach warto wiedzieć czy wyrazy rozważanego ciągu mają tendencję do skupiania się wokół jakiejś liczby. Gdyby rzeczywiście tak było, to znajomość tej liczby pozwala „zlokalizować” nasz ciąg na osi. Oznacza to, że prawie wszystkie, poza skończoną ilością, wyrazy naszego ciągu leżą w pobliżu danej liczby, którą nazywamy granicą ciągu. Fakt, że liczba jest granicą właściwą ciągu oznacza więc, że prawie wszystkie (tzn. wszystkie od pewnego miejsca) wyrazy ciągu leżą w przedziale
, a ponieważ może być dowolnie małe, tak więc dowolnie blisko liczby znajduje się nieskończenie wiele wyrazów ciągu
UWAGA
Uwaga 1: Oznaczenie
Uwaga 1: Oznaczenie
Fakt, że liczba jest granicą właściwą ciągu oznaczamy symbolicznie i mówimy, że ciąg jest zbieżny do liczby przy zmierzającym do nieskończoności.
( )
a
n( )
a
nn
n
n
ε > 0
[−ε, ε]
( )
a
ng
ε > 0
| − g| < ε
a
ng
( )
a
n(g − ε, g + ε)
ε
g
( )
a
ng
( )
a
nlim
n→∞a
n= g
( )
a
ng
n
UWAGA
Uwaga 2:
Uwaga 2:
Pojęcie granicy ciągu możemy zdefiniować formalnie
PRZYKŁAD
Przykład 1:
Przykład 1:
Pokaż, że , ,
Rozwiązanie:
Aby wykazać, że liczba jest granicą ciągu weźmiemy dowolną liczbę i wykażemy, że uda się znaleźć taką liczbę naturalną , że dla wszystkich zachodzi nierówność .
Zauważamy, że zachodzą ograniczenia dla
czyli, gdyby liczba była liczbą naturalną, to można byłoby przyjąć , ale ponieważ, z reguły, nie jest to liczba naturalna, to przyjmujemy , gdzie oznacza część całkowitą z liczby rzeczywistej . Dla tak dobranego i dowolnej liczby zachodzi wtedy nierówność , czyli , a to właśnie mieliśmy wykazać.
PRZYKŁAD
Przykład 2:
Przykład 2:
Wykaż, że dla dowolnego .
Rozwiązanie:
Dla dowolnie wybranego mamy znaleźć spełniające warunek dla i . Zauważamy, że
Jeżeli weźmiemy , to , a co za tym idzie dla .
Rysunek 2: Granica niewłaściwa ciągu
= g wtedy i tylko wtedy, gdy ∀ε > 0 ∃ ∈ N ∀n ⩾
| − g| < ε
lim
n→∞a
nn
0n
0a
n= 0
lim
n→∞ n1lim
n→∞(− ) = 0
n1lim
n→∞ (−1)= 0
n n
0
( )
a
nε > 0
n
0n ⩾ n
0| − 0| < ε
a
n| − 0| = | − − 0| = |
1− 0| = < ε
n 1n (−1) n n n1n >
1ε 1 εn
0=
1ε= [ ] + 1
n
0 1ε[x]
x
n
0n ⩾ n
0 1n< ε
| − 0| < ε
a
n= 0
lim
n→∞ n1kk > 0
ε > 0
n
0∈ N
| − 0| < ε
n1kn ⩾ n
0k > 0
| − 0| < ε ⇔
1< ε ⇔
> ε ⇔ n >
.
nk n1kn
k√
k 1ε= [
] + 1 ∈ N
n
0√
k 1εn
0>
√
k 1ε| − 0| < ε
n1kn ⩾ n
0Zauważamy, że ciągi z Rys. 2 zachowują się, przy zmierzającym do nieskończoności, inaczej niż ciąg zbieżny do pewnej granicy . Jeżeli wybierzemy dowolnie dużą liczbę , to nieskończenie wiele wyrazów ciągu pierwszego jest większych od liczby , oraz nieskończenie wiele wyrazów ciągu drugiego jest mniejszych od liczby . Z dowolności wyboru liczby wnioskujemy, że wyrazy żadnego z obydwu ciągów nie lokalizują się w pobliżu żadnej liczby rzeczywistej. Mówimy wtedy, że ciąg jest rozbieżny do
, w pierwszym przypadku, albo do , w drugim przypadku.
DEFINICJA
Definicja 2: Granica niewłaściwa
Definicja 2: Granica niewłaściwa
ciągu
ciągu
Mówimy, że ciąg ma granicę niewłaściwą , jeżeli dla dowolnej liczby od pewnego miejsca zachodzi nierówność .
DEFINICJA
Definicja 3: Granica niewłaściwa
Definicja 3: Granica niewłaściwa
ciągu
ciągu
Mówimy, że ciąg ma granicę niewłaściwą , jeżeli dla dowolnej liczby od pewnego miejsca zachodzi nierównośc .
UWAGA
Uwaga 3:
Uwaga 3:
Fakt, że ciąg ma granicę niewłaściwą oznaczamy i mówimy, że ciąg jest rozbieżny do .
Fakt, że ciąg ma granicę niewłaściwą oznaczamy i mówimy, że ciąg jest rozbieżny do .
Definicję granicy niewłaściwej możemy zapisać symbolicznie
a granicy niewłaściwej
n
g
E > 0
E
−E
E
+∞
−∞
+∞
( )
a
n+∞
E > 0
> E
a
n−∞
( )
a
n−∞
E > 0
< −E
a
n( )
a
n+∞
lim
n→∞a
n= +∞
( )
a
n+∞
( )
a
n−∞
lim
n→∞a
n= −∞
( )
a
n−∞
+∞
= +∞ wtedy i tylko wtedy, gdy ∀E > 0 ∃ ∈ N ∀n ⩾ ( > E)
lim
n→∞a
nn
0n
0a
n−∞
= −∞ wtedy i tylko wtedy, gdy ∀E > 0 ∃ ∈ N ∀n ⩾ ( < −E)
PRZYKŁAD
Przykład 3:
Przykład 3:
Pokaż, że Rozwiązanie:
Aby wykazać, że jest granicą niewłaściwą ciągu weźmiemy dowolną liczbę i wykażemy, że uda się znaleźć taką liczbę naturalną , że dla wszystkich zachodzi nierówność .
Nierówność sugeruje, że należy przyjąć , które jest liczbą naturalną większą od , czyli dla .
Aby wykazać, że jest granicą niewłaściwą ciągu weźmiemy dowolną liczbę i wykażemy, że uda się znaleźć taką liczbę naturalną , że dla wszystkich zachodzi nierówność .
Nierówność jest równoważna nierówności , czyli wykorzystujemy dobrane dla poprzedniego ciągu.
PRZYKŁAD
Przykład 4:
Przykład 4:
Wykaż, że dla .
Rozwiązanie:
Dla dowolnie wybranego mamy znaleźć , takie, że nierówność jest spełniona dla wszystkich i .
Zauważamy, że dla zachodzi , czyli dla i wszystkich zachodzi żądana nierówność .
500
-500
10 20 30 40
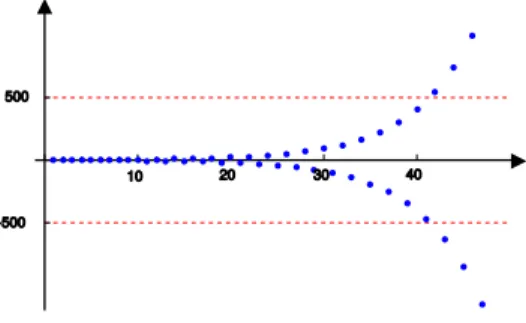
Rysunek 3: Ciąg rozbieżny
Na Rys. 3 widzimy wykres ciągu, który ma nieskończenie wiele wyrazów, większych od dowolnie wybranej liczby , ale równocześnie ma też nieskończenie wiele wyrazów, które są mniejsze od liczby . Wyrazy tego ciągu nie tylko nie lokalizują się wokół żadnej liczby rzeczywistej, ale również nie spełniają definicji ciągu rozbieżnego do , ani do . Taki ciąg nazywamy ciągiem rozbieżnym, albo ciągiem, który nie ma granicy.
n = +∞,
(−n) = −∞.
lim
n→∞lim
n→∞+∞
( )
a
nE > 0
n
0n ⩾ n
0a
n> E
n > E
n
0= [E] + 1
E
n > E
n ⩾ n
0−∞
( )
a
nE > 0
n
0n ⩾ n
0a
n< −E
−n < −E
n > E
n
0= [E] + 1
= +∞
lim
n→∞n
kk > 0
E > 0
n
0∈ N
n
k> E
n ⩾ n
0k > 0
k > 0
n
k> E ⇔ n >
E
1kn
0= [
E
1k] + 1
n ⩾ n
0> E
n
kE > 0
– E
+∞
−∞
DEFINICJA
Definicja 4: Ciąg rozbieżny
Definicja 4: Ciąg rozbieżny
Ciąg, który nie posiada granicy właściwej ani niewłaściwej nazywamy ciągiem rozbieżnym.
PRZYKŁAD
Przykład 5:
Przykład 5:
Wykaż, że ciąg jest rozbieżny. Rozwiązanie:
Zauważamy, że ciąg przyjmuje na zmianę wartości albo .
Nie może to być ciąg rozbieżny do , bo dla żaden wyraz ciągu nie jest większy od E i analogicznie nie może być rozbieżny do , bo żaden wyraz ciągu nie jest mniejszy od .
Żadna liczba rzeczywista g różna od i nie może też być granicą właściwą ciągu , bo jeżeli wybierzemy przedział , który nie zawiera liczb i , to nie zawiera też żadnego wyrazu naszego ciągu. Liczba też nie może być granicą właściwą ciągu , ponieważ poza przedziałem , który nie zawiera liczby leży nieskończenie wiele wyrazów naszego ciągu. Analogicznie liczba nie może być granicą właściwą ciągu .
Zatem ciąg nie ma zarówno granicy właściwej, jak i niewłaściwej, czyli jest rozbieżny.
Publikacja udostępniona jest na licencji Creative Commons Uznanie autorstwa - Na tych samych warunkach 3.0 Polska. Pewne prawa zastrzeżone na rzecz autorów i Akademii Górniczo-Hutniczej. Zezwala się na dowolne wykorzystanie treści publikacji pod warunkiem wskazania autorów i Akademii Górniczo-Hutniczej jako autorów oraz podania informacji o licencji tak długo, jak tylko na utwory zależne będzie udzielana taka sama licencja. Pełny tekst licencji dostępny na stronie
http://creativecommons.org/licenses/by-sa/3.0/pl/.
Data generacji dokumentu: 2019-04-15 05:00:59
Oryginalny dokument dostępny pod adresem: https://epodreczniki.open.agh.edu.pl/openagh-permalink.php? link=85204f5b7406eeef4d906b3fdf748eb7
Autor: Katarzyna Czyżewska